可转债全部历史因子数据,提供api支持
今天在写可转债系统,顺便下载了一下服务器的可转债数据,给大家研究使用
from trader_tool.stock_data import stock_datafrom trader_tool.lude_data_api import lude_data_apiimport osclass convertible_bond_back_test_system:'''可转债回测系统'''def __init__(self,start_date='20180101',end_date='20240612'):self.start_date=start_dateself.end_date=end_dateself.path=os.path.dirname(os.path.abspath(__file__))self.lude_data_api=lude_data_api()self.stock_data=stock_data()def down_all_data(self):'''下载服务器可转债全部数据'''trader_list=self.stock_data.get_trader_date_list(start_date=self.start_date,end_date=self.end_date)for date in trader_list:all_path=os.listdir(r'{}\data'.format(self.path))main_path='{}.csv'.format(date)if main_path in all_path:print('{}已经下载'.format(main_path))else:df=self.lude_data_api.get_bond_data(date=date)stats=df['数据状态'].tolist()[-1]if stats==True:try:del df['更新时间']except Exception as e:print(e)try:del df['数据时间']except Exception as e:print(e)df.to_csv(r'{}\data\{}'.format(self.path,main_path))print('{}交易日数据下载完成'.format(date))else:print('{}交易日没有数据'.format(date))if __name__=='__main__':backtrader=convertible_bond_back_test_system()backtrader.down_all_data()
原始的数据来自禄得,不用在商业用途,感谢老师的数据
网页 https://lude.cc/
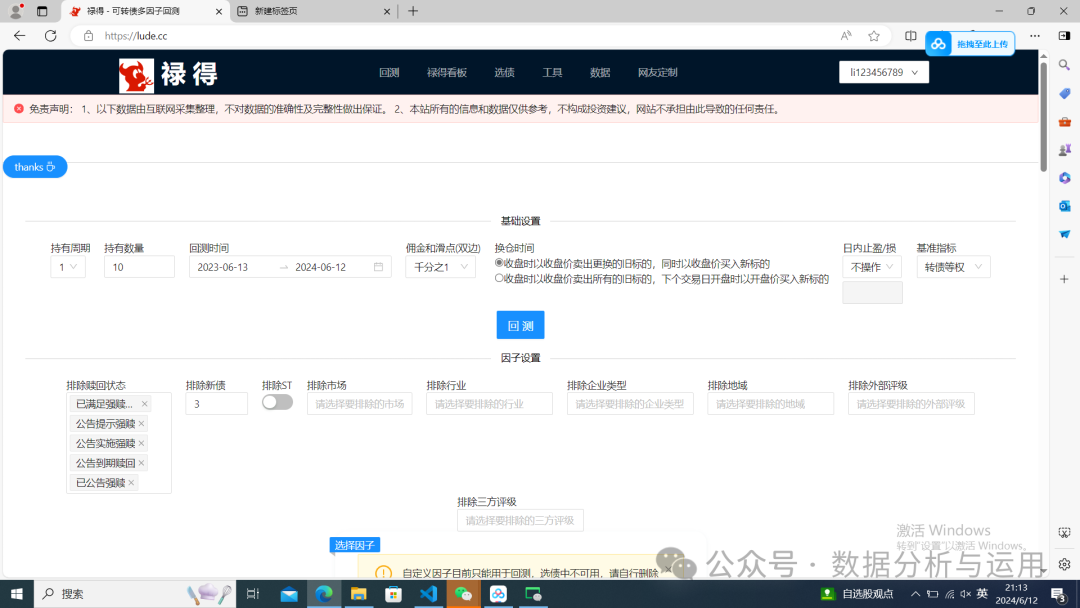
我网页也支持数据下载 网页 http://120.78.132.143:8023/
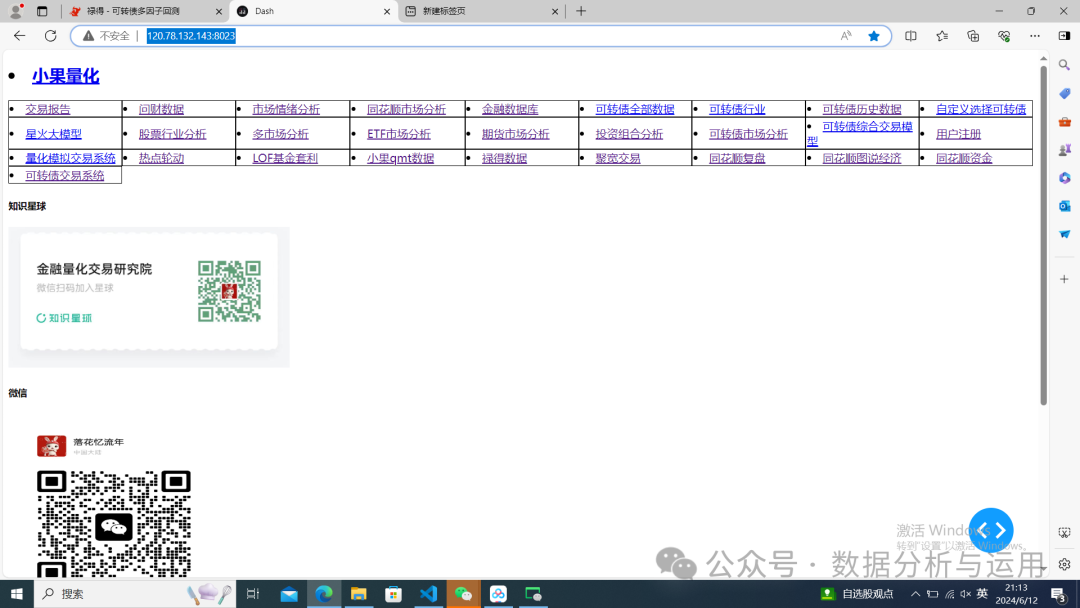
点击可转债数据,禄得数据
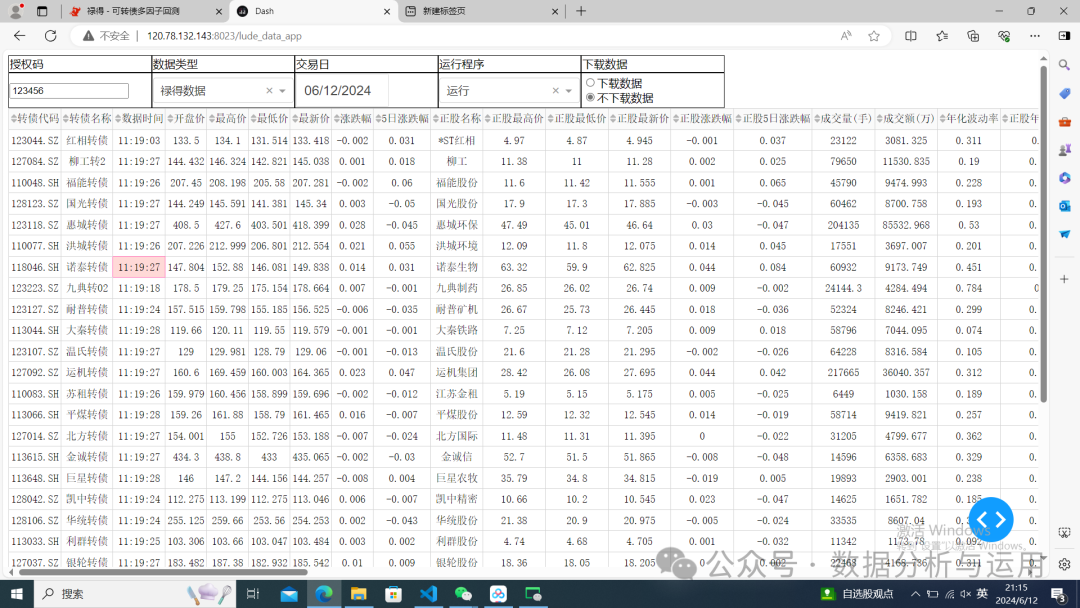
可以点击下载数据,选择日期
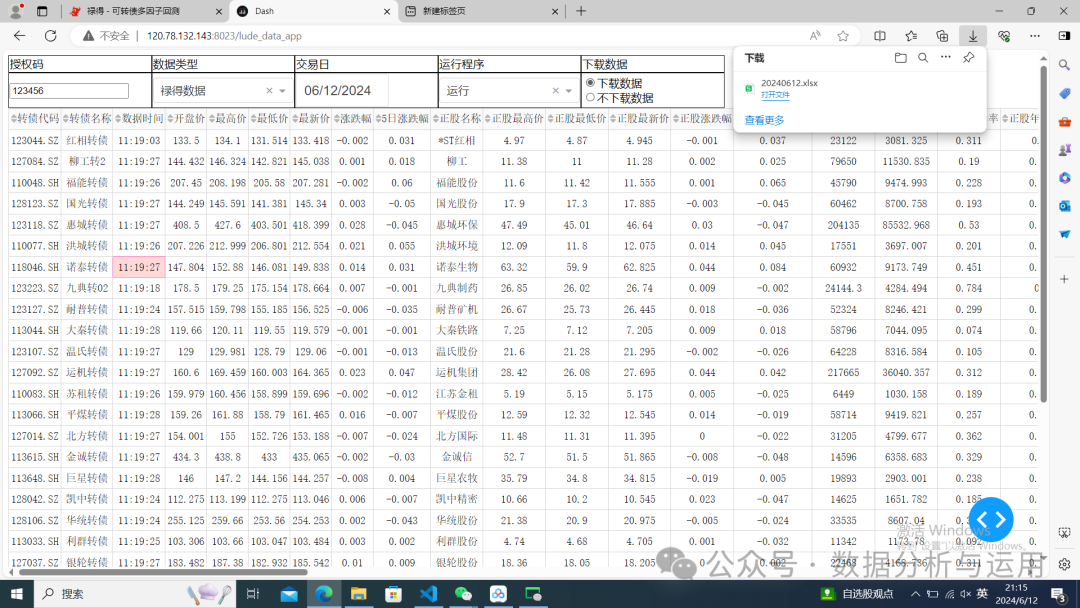
下载的数据
利用程序自动下载全部历史的数据
全部的历史数据
需要全部数据的直接回复20240612就可以

下载我服务器数据的api
import pandas as pdimport requestsimport jsonclass lude_data_api:def __init__(self,url='http://120.78.132.143',port='8023',password='123456'):'''手动下载存数据库禄得数据apiurl服务器port端口password授权码'''self.url=urlself.port=portself.password=passworddef get_bond_data(self,date='2024-04-26'):'''获取可转债数据'''url='{}:{}/_dash-update-component'.format(self.url,self.port)headers={'Content-Type':'application/json'}data={"output":"lude_data_maker_table.data@669dd4696a628d8290353c138057eb97","outputs":{"id":"lude_data_maker_table","property":"data@669dd4696a628d8290353c138057eb97"},"inputs":[{"id":"password","property":"value","value":self.password},{"id":"lude_data_data_type","property":"value","value":"禄得数据"},{"id":"lude_data_end_date","property":"date","value":date},{"id":"lude_data_run","property":"value","value":"运行"},{"id":"lude_data_down_data","property":"value","value":"不下载数据"}],"changedPropIds":["lude_data_run.value"]}res=requests.post(url=url,data=json.dumps(data),headers=headers)text=res.json()df=pd.DataFrame(text['response']['lude_data_maker_table']['data'])return dfdef get_bond_spot_data(self,date='2024-05-23'):'''获取可转债实时数据'''url='{}:{}/_dash-update-component'.format(self.url,self.port)headers={'Content-Type':'application/json'}data={"output":"lude_data_maker_table.data@669dd4696a628d8290353c138057eb97","outputs":{"id":"lude_data_maker_table","property":"data@669dd4696a628d8290353c138057eb97"},"inputs":[{"id":"password","property":"value","value":self.password},{"id":"lude_data_data_type","property":"value","value":"实时数据"},{"id":"lude_data_end_date","property":"date","value":date},{"id":"lude_data_run","property":"value","value":"运行"},{"id":"lude_data_down_data","property":"value","value":"不下载数据"}],"changedPropIds":["lude_data_run.value"]}res=requests.post(url=url,data=json.dumps(data),headers=headers)text=res.json()df=pd.DataFrame(text['response']['lude_data_maker_table']['data'])return dfif __name__=='__main__':models=lude_data_api()df=models.get_bond_data(date='2024-05-23')print(df)df=models.get_bond_spot_data(date='2024-05-23')
相关文章:

可转债全部历史因子数据,提供api支持
今天在写可转债系统,顺便下载了一下服务器的可转债数据,给大家研究使用 from trader_tool.stock_data import stock_datafrom trader_tool.lude_data_api import lude_data_apiimport osclass convertible_bond_back_test_system: 可转债回测系统…...

Python | C++ | MATLAB | Julia | R 市场流动性数学预期评估量
🎯要点 🎯市场流动性策略代码应用:🎯动量策略:滚动窗口均值策略、简单移动平均线策略、指数加权移动平均线策略、相对强弱指数、移动平均线收敛散度交叉策略、三重指数平均策略、威廉姆斯 %R 策略 | 🎯均值…...

Android 常用开源库 MMKV 源码分析与理解
文章目录 前言一、MMKV简介1.mmap2.protobuf 二、MMKV 源码详解1.MMKV初始化2.MMKV对象获取3.文件摘要的映射4.loadFromFile 从文件加载数据5.数据写入6.内存重整7.数据读取8.数据删除9.文件回写10.Protobuf 实现1.序列化2.反序列化 12.文件锁1.加锁2.解锁 13.状态同步 总结参考…...
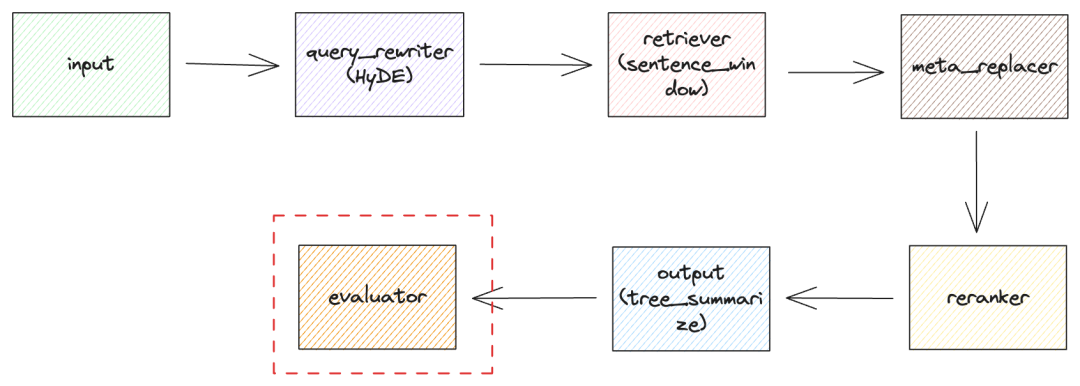
大模型高级 RAG 检索策略之流程与模块化
我们介绍了很多关于高级 RAG(Retrieval Augmented Generation)的检索策略,每一种策略就像是机器中的零部件,我们可以通过对这些零部件进行不同的组合,来实现不同的 RAG 功能,从而满足不同的需求。 今天我们…...

TCPListen客户端和TCPListen服务器
创建项目 TCPListen服务器 public Form1() {InitializeComponent();//TcpListener 搭建tcp服务器的类,基于socket套接字通信的//1创建服务器对象TcpListener server new TcpListener(IPAddress.Parse("192.168.107.83"), 3000);//2 开启服务器 设置最大…...

DDei在线设计器-属性编辑器
DDei-Core-属性编辑器 DDei-Core-属性编辑器插件包含了文本、大文本、数值、下拉、单选、勾选以及颜色等属性编辑。 图形和属性共同构成一个完整的定义,属性编辑器就是编辑属性值的控件。当选中图形实例时,属性面板就会展现当前实例的所有属性以及属性编…...

八字综合测算网整站源码程序/黄历/灵签/排盘/算命/生肖星座/日历网/周公解梦
八字综合测算网整站源码程序/黄历/灵签/排盘/算命/生肖星座/日历网/周公解梦 演示地址: https://s24.gvyun.com/ 手机端地址: https://ms24.gvyun.com/ 网站功能分类: 八字:八字测算;日干论命;称骨论命…...
—— 布局管理)
C# WPF入门学习主线篇(十一)—— 布局管理
C# WPF入门学习主线篇(十一)—— 布局管理 欢迎来到C# WPF入门学习系列的第十一篇。在前面的文章中,我们已经探讨了WPF中的许多控件及其属性和事件。今天,我们将开启一个新的篇章——布局管理。布局管理是WPF中一个至关重要的概念…...

LabVIEW轴承试验机测控系统
开发了一种基于LabVIEW软件开发的大功率风电机组增速箱轴承试验机测控系统。系统主要用于模拟实际工况,进行轴承可靠性分析,以优化风电机组的性能和可靠性。通过高度自动化的测控系统,实现了对试验机的精确控制,包括速度、振动、温…...
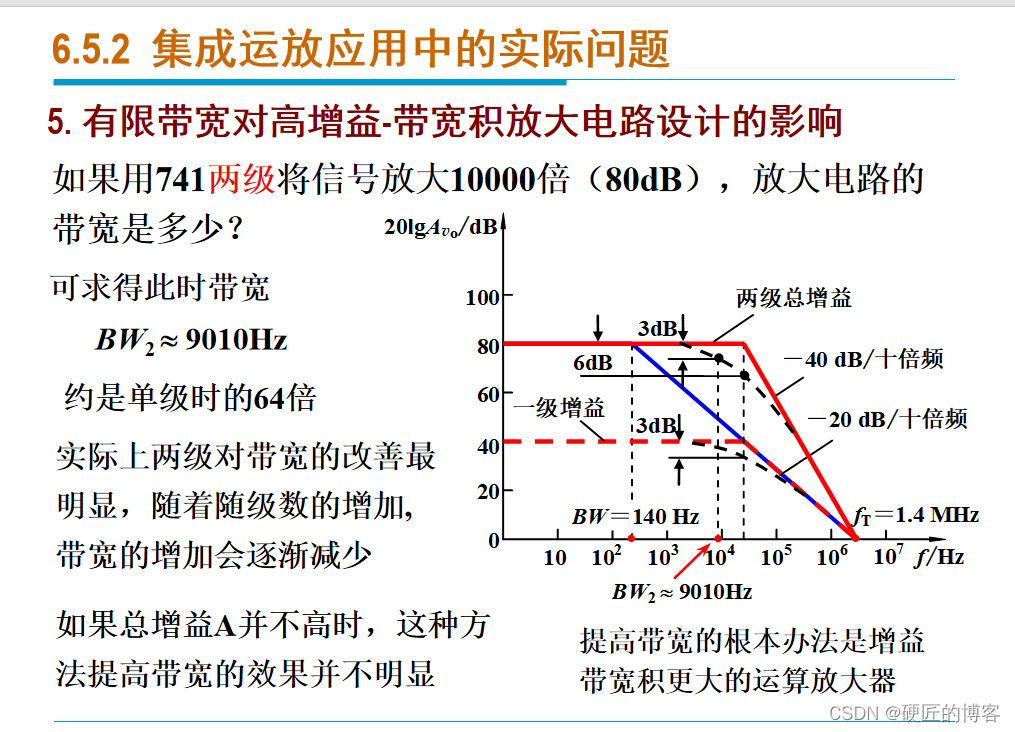
0605 实际集成运算放大器的主要参数和对应用电路的影响
6.5.1 实际集成运放的主要参数 6.5.2 集成运放应用中的实际问题 6.5.2 集成运放应用中的实际问题...
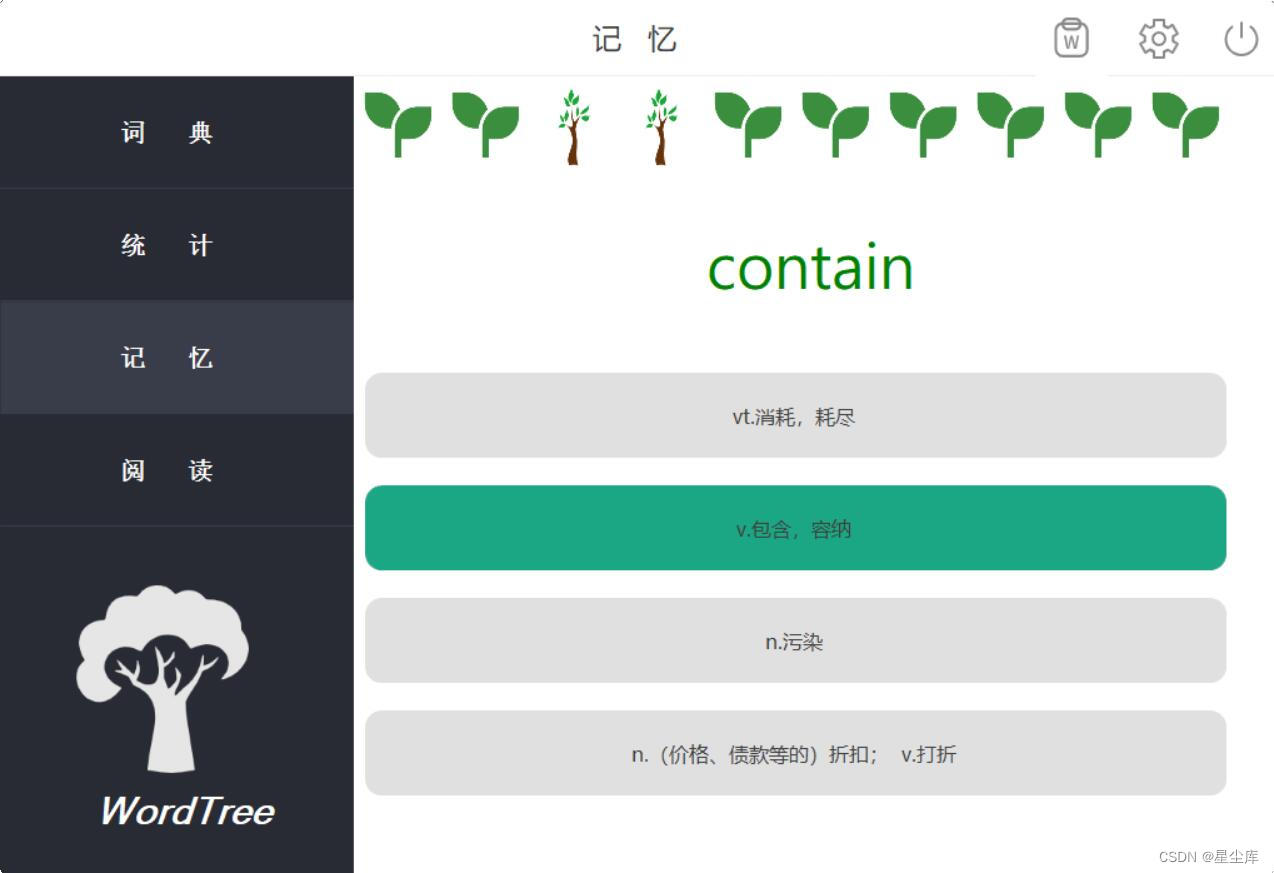
艾宾浩斯winform单词系统+mysql
为用户提供集词典、题库、记忆单词功能于一体的应用,为用户提供目的性强、科学高效、多样化的记忆单词方法,使用户学习英语和记忆单词的效率得到提高 单词记忆模块 管理模块 查询单词 阅读英文 查看词汇 记忆单词 收藏单词 字段管理设置 统计 艾宾浩斯wi…...

rv1126-rv1109-串口显示路径不变化
串口只有#, 后来看了教程改成如下 但是没有变化,那个路径都只显示rootLonbon# 于是最后改成了这样 因为:...

基于C#开发web网页管理系统模板流程-主界面密码维护功能完善
点击返回目录-> 基于C#开发web网页管理系统模板流程-总集篇-CSDN博客 前言 紧接上篇->基于C#开发web网页管理系统模板流程-主界面统计功能完善-CSDN博客 一个合格的管理系统,至少一定存在一个功能——用户能够自己修改密码,理论上来说密码只能有用…...

[NOVATEK] NT96580行车记录仪功能学习笔记(持续更新~
sdk文件结构(我个人理解) 1、DX文件夹里面是IO口以及项目使用到的相关外设配置 2、GX是外设功能实现函数所在文件夹 3、Startup文件夹是整个项目的入口,里面有个startup.c文件是main函数所在 4、UIAPP是手机APP功能设置的文件夹,增删改功能主要是在UIAPP和UIWnd文件夹里…...

力扣752. 打开转盘锁
Problem: 752. 打开转盘锁 文章目录 题目描述思路及解法复杂度Code 题目描述 思路及解法 1.用一个集合 deads 存储所有的“死锁”状态,一个集合 visited 存储所有已经访问过的状态,以避免重复访问,一个队列 q 进行广度优先搜索(BF…...

揭秘:义乌理阳的跨境选品师项目
在全球经济一体化的今天,跨境电商已成为各国贸易的重要组成部分,而选品师作为其中的关键角色,扮演着挑选优质商品的重要角色。在中国义乌,一家名为理阳信息咨询服务有限公司备受关注,因其据称拥有跨境选品师项目而备受…...

电视剧推荐
1、《春色寄情人》 2、《唐朝诡事录》 3、《南来北往》 4、《与凤行》 5、《利剑玫瑰》 6、《承欢记》...

ISO 19115-3:2023 关于元数据最小实例的允许命名空间的详细说明
理解说明内容 标识符(Identifier) URL: https://standards.isotc211.org/19115/-1/1/req/metadata-minimal-xml/allowed-namespaces解释: 这个 URL 标识了元数据最小实例中允许的命名空间的具体标准和规范。包含于(Included in) 要求类 4:元数据信息最小交换 (ISO 19115-…...
最新下载:CorelDraw 2023【软件附加安装教程】
简介: CorelDRAW Graphics Suite 订阅版拥有配备齐全的专业设计工具包,可以通过非常高的效率提供令人惊艳的矢量插图、布局、照片编辑和排版项目。价格实惠的订阅就能获得令人难以置信的持续价值,即时、有保障地获得独家的新功能和内容、一流…...
QT系列教程(8) QT 布局学习
简介 Qt 中的布局有三种方式,水平布局,垂直布局,栅格布局。 通过ui设置布局 我们先创建一个窗口应用程序,程序名叫layout,基类选择QMainWindow。但我们不使用这个mainwindow,我们创建一个Qt应用程序类Log…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
