第五十一天 | 1143.最长公共子序列
题目:1143.最长公共子序列718.最长重复子数组的区别是,子序列不要求连续,子数组要求连续。这一差异体现在dp数组含义和递推公式中,本题是子序列,那就要考虑上nums1[i - 1] != nums2[j - 1]的情况。
本道题与
1.dp数组含义:
dp[i][j]:本题是子序列,那么dp数组的含义是长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]。上一题是子数组,那么dp数组的含义是以dp[i - 1]和dp[j - 1]结尾的最长的重复子数组
这样定义是为了后面代码实现方便,如果非要定义为长度为[0, i]的字符串text1也可以,我在 动态规划:718. 最长重复子数组 (opens new window)中的「拓展」里 详细讲解了区别所在,其实就是简化了dp数组第一行和第一列的初始化逻辑。
2.递推公式:
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
3.dp数组如何初始化
先看看dp[i][0]应该是多少呢?
test1[0, i-1]和空串的最长公共子序列自然是0,所以dp[i][0] = 0;
同理dp[0][j]也是0。
其他下标都是随着递推公式逐步覆盖,初始为多少都可以,那么就统一初始为0。
4.确定遍历顺序
从递推公式,可以看出,有三个方向可以推出dp[i][j],如图:
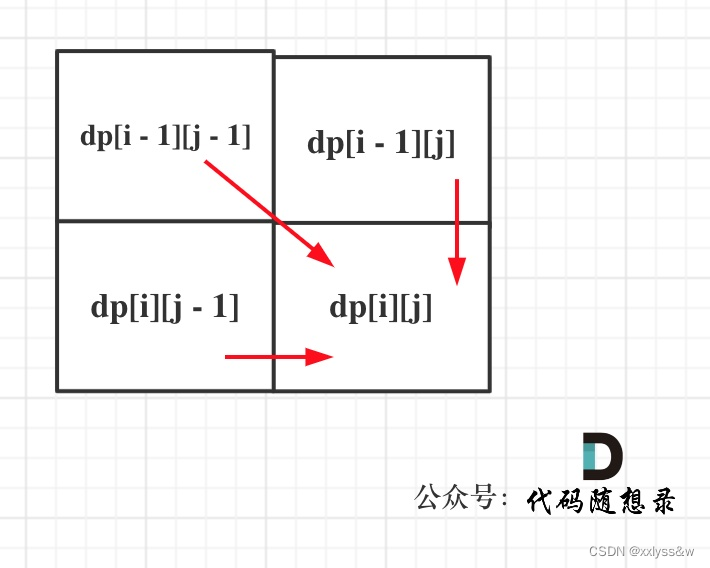
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵
dp[text1.size()][text2.size()]为最终结果
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:dp = [[0] * (len(text2) + 1) for _ in range (len(text1) + 1)]for i in range(1, len(text1) + 1):for j in range(1, len(text2) + 1):if text1[i - 1] == text2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else: dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])return dp[len(text1)][len(text2)]相关文章:

第五十一天 | 1143.最长公共子序列
题目:1143.最长公共子序列718.最长重复子数组的区别是,子序列不要求连续,子数组要求连续。这一差异体现在dp数组含义和递推公式中,本题是子序列,那就要考虑上nums1[i - 1] ! nums2[j - 1]的情况。 本道题与 1.dp数组…...

未来的5-10年,哪些行业可能会被AI代替?
在未来的5-10年,多个行业可能会受到AI技术的影响,其中一些工作可能会被AI所代替。以下是对可能被AI替代的行业及工作的一些概述: 客户服务与代表:随着AI技术的发展,特别是自动话术对话和语音生成技术的进步࿰…...

据报道,FTC 和 DOJ 对微软、OpenAI 和 Nvidia 展开反垄断调查
据《纽约时报》报道,联邦贸易委员会 (FTC) 和司法部 (DOJ) 同意分担调查微软、OpenAI 和 Nvidia 潜在反垄断违规行为的职责。 美国司法部将牵头对英伟达进行调查,而联邦贸易委员会将调查 OpenAI 与其最大投资者微软之间的交易。 喜好儿网 今年 1 月&a…...

人工智能发展历程和工具搭建学习
目录 人工智能的三次浪潮 开发环境介绍 Anaconda Anaconda的下载和安装 下载说明 安装指导 模块介绍 使用Anaconda Navigator Home界面介绍 Environment界面介绍 使用Jupter Notebook 打开Jupter Notebook 配置默认目录 新建文件 两种输入模式 Conda 虚拟环境 添…...

Dijkstra算法的原理
Dijkstra算法的原理可以清晰地分为以下几个步骤和要点: 初始化: 引入一个辅助数组D,其中D[i]表示从起始点(源点)到顶点i的当前已知最短距离。如果起始点与顶点i之间没有直接连接,则D[i]被初始化为无穷大&a…...
maven引入依赖时莫名报错
一般跟依赖的版本无关,会报出 Cannot resolve xxx 的错误。 这种情况下去IDEA的setting中找maven的仓库位置 在仓库中顺着包路径下寻找,可能会找到.lastUpdated 的文件,这样的文件一般是下载失败了,而且在一段时间内不再下载&…...

graalvm编译springboot3 native应用
云原生时代容器先行,为了更好的拥抱云原生,spring boot3之后,推出了graalvm编译boot项目,利用jvm的AOT( Ahead Of Time )运行前编译技术,可以将javay源码直接构建成机器码二进制的文件ÿ…...

代码随想录Day58
392.判断子序列 题目:392. 判断子序列 - 力扣(LeetCode) 思路:定义重合数记录s与t的比对情况,挨个取出t的字符,与s的字符进行比较,如果相同,重合数就加1,跳到s的下一个字…...
 与 dm-verity 之间的关系、相同点与差异点)
Android Verified Boot (AVB) 与 dm-verity 之间的关系、相同点与差异点
标签: AVB; dm-verity ;Android Android Verified Boot (AVB) 与 dm-verity 之间的关系、相同点与差异点 概述 Android Verified Boot (AVB) 和 dm-verity 是 Android 操作系统中用于确保设备启动过程和运行时数据完整性的两个重要技术。尽管它们有着不同的实现和侧重点,…...

C++学习笔记“类和对象”:多态;
目录 4.7 多态 4.7.1 多态的基本概念 4.7.2 多态案例--计算器类 4.7.3 纯虚函数和抽象类 4.7.4 多态案例二 - 制作饮品 4.7.5 虚析构和纯虚析构 4.7.6 多态案例三-电脑组装 4.7 多态 4.7.1 多态的基本概念 多态是C面向对象三大特性之一 多态分为两类 静志多态: 函数…...
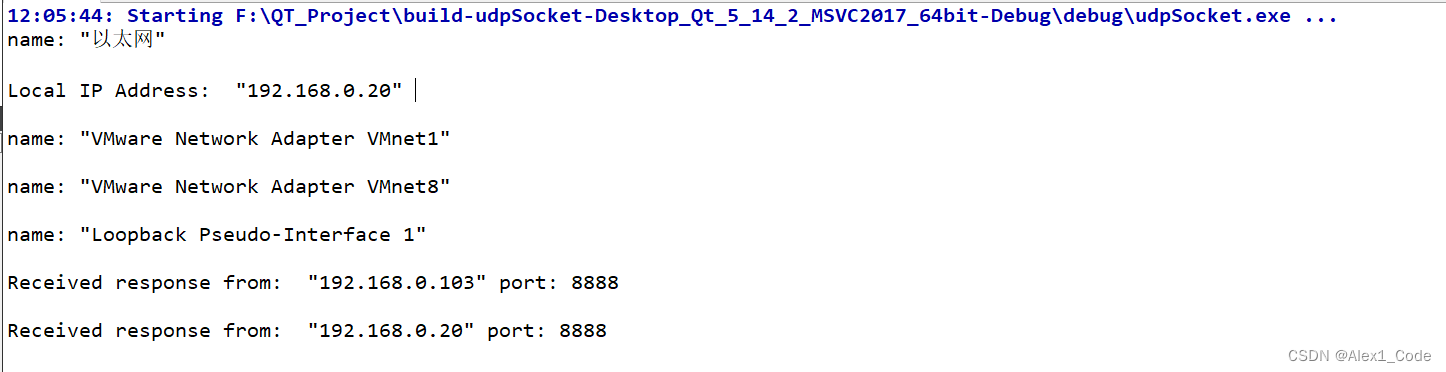
QT Udp广播实现设备发现
测试环境 本文选用pc1作为客户端,pc2,以及一台虚拟机作为服务端。 pc1,pc2(客户端): 虚拟机(服务端): 客户端 原理:客户端通过发送广播消息信息到ip:255.255.255.255(QHostAddress::Broadcast),局域网…...

PyTorch 统计属性-Tensor基本操作
最小 min, 最大 max, 均值 mean,累加 sum,累乘 prod … >>> a torch.arange(0,8).view(2,4).float() >>> a tensor([[0., 1., 2., 3.],[4., 5., 6., 7.]])>>> a.min() ## 最小值:tensor(0.) >>> a.ma…...
波拉西亚战记加速器 台服波拉西亚战记免费加速器
波拉西亚战记是一款新上线的MMORPG游戏,游戏内我们有多个角色职业可以选择,可以体验不同的战斗流派玩法,开放式的地图设计,玩家可以自由的进行探索冒险,寻找各种物资。各种随机事件可以触发,让玩家的冒险过…...

Mocha + Chai 测试环境配置,支持 ES6 语法
下面是一个完整的 Mocha Chai 测试环境配置,支持 ES6 语法。我们将使用 Babel 来转译 ES6 代码。 步骤一:初始化项目 首先,在项目目录中运行以下命令来初始化一个新的 Node.js 项目: npm init -y步骤二:安装必要的…...

华为网络设备攻击防范
畸形报文攻击防范 攻击行为 畸形报文攻击是通过向交换机发送有缺陷的IP报文,使得交换机在处理这样的IP包时会出现崩溃,给交换机带来损失。 畸形报文攻击主要有如下几种: 没有IP载荷的泛洪攻击 IGMP空报文攻击 LAND攻击 Smurf攻击 TCP标…...

RK3588开发笔记-100M网口自协商成1000M网口
目录 前言 一、问题描述 二、原理图连接 三、解决方法 总结 前言 在进行RK3588开发过程中,遇到一个令人困惑的问题:在使用RTL8211F-CG phy芯片出来的100M网口在自协商后连接速率变成了1000M。这篇博客将详细记录这个问题的产生、排查过程以及最终的解决方案,希望能对遇到…...
Python第二语言(十三、PySpark实战)
目录 1.开篇 2. PySpark介绍 3. PySpark基础准备 3.1 PySpark安装 3.2 掌握PySpark执行环境入口对象的构建 3.3 理解PySpark的编程模型 4. PySpark:RDD对象数据输入 4.1 RDD对象概念:PySpark支持多种数据的输入,完成后会返回RDD类的对…...

《阅读的方法》读后感——超越期待的收获
当我翻开这本书的扉页时,未曾料到它会给我带来如此深远的启示和收获。依照推荐序言中的指引,我随意翻阅、精心选读,每一次都如同打开一扇新的窗户,让我窥见不同领域的智慧和美好。 等地铁时、临睡前随便读点什么,有什么…...
)
算法训练营第五十八天 | LeetCode 392 判断子序列、卡码网模拟美团笔试第一、二、三题(300/500有待提高)
卡码网图论更新了可以去看看,模拟笔试第四题就是深搜/广搜还不太会 LeetCode 392 判断子序列 其实就是最长公共子序列翻版 代码如下: class Solution {public boolean isSubsequence(String s, String t) {int[][] dp new int[s.length() 1][t.lengt…...
Sa-Token鉴权与网关服务实现
纠错: 在上一部分里我完成了微服务框架的初步实现,但是先说一下之前有一个错误,就是依赖部分 上次的学习中我在总的父模块下引入了spring-boot-dependencies(版本控制)我以为在子模块下就不需要再引用了,…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...

多模态大语言模型arxiv论文略读(110)
CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文标题:CoVLA: Comprehensive Vision-Language-Action Dataset for Autonomous Driving ➡️ 论文作者:Hidehisa Arai, Keita Miwa, Kento Sasaki, Yu Yamaguchi, …...

[C++错误经验]case语句跳过变量初始化
标题:[C错误经验]case语句跳过变量初始化 水墨不写bug 文章目录 一、错误信息复现二、错误分析三、解决方法 一、错误信息复现 write.cc:80:14: error: jump to case label80 | case 2:| ^ write.cc:76:20: note: crosses initialization…...
