spark MLlib (DataFrame-based) 中的聚类算法Bisecting K-Means、K-Means、Gaussian Mixture
Bisecting K-Means
核心原理:
Bisecting K-Means 是一种层次 K-Means 聚类算法,基于 Steinbach、Karypis 和 Kumar 的论文《A comparison of document clustering techniques》,并对 Spark 环境进行了修改和适应。
该算法通过递归地将数据集分割为二叉树结构的子集群来执行聚类。开始时,整个数据集视为单个聚类,然后通过以下步骤逐步分割:
- 选择当前具有最大 SSE(Sum of Squared Errors)的聚类进行分割。
- 在选定的聚类中执行 K-Means 聚类,根据距离选择最佳的分割点。
这种分割方法不断重复,直到达到预定的聚类数量或无法进一步分割。
数学表达式:
对于 Bisecting K-Means,其核心是基于 K-Means 的分割操作,数学表达式如下所示:
C = arg min C ∑ i = 1 k ∑ x ∈ C i ∥ x − μ i ∥ 2 \mathbf{C} = \arg \min_{C} \sum_{i=1}^{k} \sum_{\mathbf{x} \in C_i} \|\mathbf{x} - \mathbf{\mu}_i\|^2 C=argCmini=1∑kx∈Ci∑∥x−μi∥2
其中:
- ( C ) ( \mathbf{C} ) (C) 表示聚类结果,包含 ( k ) ( k ) (k) 个聚类 ( C i ) ( C_i ) (Ci)。
- ( x ) ( \mathbf{x} ) (x) 是数据点。
- ( μ i ) ( \mathbf{\mu}_i ) (μi) 是第 ( i ) ( i ) (i) 个聚类 ( C i ) ( C_i ) (Ci) 的中心点。
K-Means
核心原理:
K-Means 是一种经典的聚类算法,通过最小化每个聚类中所有数据点与其所属聚类中心点之间的平方距离的总和来进行聚类。
该算法的步骤如下:
- 初始化:随机初始化 ( k ) ( k ) (k) 个聚类中心点。
- 迭代优化:
- 将每个数据点分配到最近的聚类中心。
- 更新每个聚类中心为其分配的所有数据点的平均值。
- 重复以上两步,直到收敛(即聚类中心不再变化或变化很小)。
数学表达式:
K-Means 的优化目标是最小化以下损失函数:
C = arg min C ∑ i = 1 k ∑ x ∈ C i ∥ x − μ i ∥ 2 \mathbf{C} = \arg \min_{C} \sum_{i=1}^{k} \sum_{\mathbf{x} \in C_i} \|\mathbf{x} - \mathbf{\mu}_i\|^2 C=argCmini=1∑kx∈Ci∑∥x−μi∥2
其中:
- ( C ) ( \mathbf{C} ) (C) 表示聚类结果,包含 ( k ) ( k ) (k) 个聚类 ( C i ) ( C_i ) (Ci)。
- ( x ) ( \mathbf{x} ) (x) 是数据点。
- ( μ i ) ( \mathbf{\mu}_i ) (μi) 是第 ( i ) ( i ) (i) 个聚类 ( C i ) ( C_i ) (Ci) 的中心点。
Gaussian Mixture
核心原理:
高斯混合模型(Gaussian Mixture Model,GMM)是一种概率模型,假设数据是由多个高斯分布组成的混合体。每个高斯分布代表一个聚类,数据点是从这些高斯分布中生成的。
GMM 通过最大化似然函数来估计模型参数,即数据点出现的概率:
Θ = arg max Θ ∑ i = 1 n log ( ∑ j = 1 k π j N ( x i ∣ μ j , Σ j ) ) \mathbf{\Theta} = \arg \max_{\Theta} \sum_{i=1}^{n} \log \left( \sum_{j=1}^{k} \pi_j \mathcal{N}(\mathbf{x}_i | \mathbf{\mu}_j, \mathbf{\Sigma}_j) \right) Θ=argΘmaxi=1∑nlog(j=1∑kπjN(xi∣μj,Σj))
其中:
- ( Θ ) ( \mathbf{\Theta} ) (Θ) 是 GMM 的参数集合,包括每个高斯分布的均值 ( μ j ) ( \mathbf{\mu}_j ) (μj)、协方差矩阵 ( Σ j ) ( \mathbf{\Sigma}_j ) (Σj) 和混合系数 ( π j ) ( \pi_j ) (πj)。
- ( x i ) ( \mathbf{x}_i ) (xi) 是数据点。
- ( N ( x ∣ μ j , Σ j ) ) ( \mathcal{N}(\mathbf{x} | \mathbf{\mu}_j, \mathbf{\Sigma}_j) ) (N(x∣μj,Σj)) 是第 ( j ) ( j ) (j) 个高斯分布的概率密度函数。
这些算法分别用于不同的数据特性和应用场景,可以根据数据的特征选择合适的聚类算法。
相关文章:
 中的聚类算法Bisecting K-Means、K-Means、Gaussian Mixture)
spark MLlib (DataFrame-based) 中的聚类算法Bisecting K-Means、K-Means、Gaussian Mixture
Bisecting K-Means 核心原理: Bisecting K-Means 是一种层次 K-Means 聚类算法,基于 Steinbach、Karypis 和 Kumar 的论文《A comparison of document clustering techniques》,并对 Spark 环境进行了修改和适应。 该算法通过递归地将数据集…...

天降流量于雀巢?元老品牌如何创新营销策略焕新生
大家最近有看到“南京阿姨手冲咖啡”的视频吗?三条雀巢速溶咖啡入杯,当面加水手冲,十元一份售出,如此朴实的售卖方式迅速在网络上走红。而面对这一波天降的热度,雀巢咖啡迅速做出了回应,品牌组特地去到了阿…...

新疆在线测宽仪配套软件实现的9大功能!
在线测宽仪可应用于各种热轧、冷轧板带材的宽度尺寸检测,材质不限,木质、钢制、铁质、金属、纸质、塑料、橡胶等都可以进行无损非接触式的检测,在各式各样的产线应用中,有些厂家,需要更加详尽完备的分析信息࿰…...
考研计组chap3存储系统
目录 一、存储器的基本概念 80 1.按照层次结构 2.按照各种分类 (41)存储介质 (2)存取方式 (3)内存是否可更改 (4)信息的可保存性 (5)读出之后data是否…...
杨氏矩阵和杨辉三角的空间复杂度较小的解题思路
文章目录 题目1 杨氏矩阵题目2 杨辉三角 题目1 杨氏矩阵 有一个数字矩阵,矩阵的每行从左到右是递增的,矩阵从上到下是递增的,请编写程序在这样的矩阵中查找某个数字是否存在。 要求:时间复杂度小于O(N); 思路: 我们可以通过题目…...

【第六篇】SpringSecurity的权限管理
一、权限管理的实现 服务端的各种资源要被SpringSecurity的权限管理控制可以通过注解和标签两种方式来处理。 放开了相关的注解后在Controller中就可以使用相关的注解来控制了 JSR250注解 /*** JSR250*/ @Controller @RequestMapping("/user") public class UserC…...

未来工作场所:数字化转型的无限可能
探索技术如何重塑我们的工作环境与协作方式 引言 在21世纪的第三个十年,数字化转型已不再仅仅是科技公司的专利,它如同一股不可阻挡的潮流,深刻地渗透到了每一个行业的血脉之中。从灵活的远程办公模式到工作流程的智能化重构,技术…...

Landsat8的质量评估波段的一个应用
Landsat8一直是遥感界的热门话题。这不仅延续了自1972年以来NASA连续对地观测,而且这颗卫星为科学界带来了一些新的东西——质量评估波段(the Quality Assessment (QA) Band)。根据USGS Landsat Missions webpage,“QA通过标示哪个…...

OpenZeppelin Ownable合约 怎么使用
文章目录 智能合约的访问控制Ownable合约使用方法 智能合约的访问控制 熟悉OpenZeppelin的智能合约库的开发者都知道这个库已经提供了根据访问等级进行访问限制的选项,其中最常见的就是Ownable合约管理的onlyOwner模式,另一个是OpenZeppelin的Roles库&a…...
)
vue3框架基本使用(基础指令)
一、响应式数据 1.ref ref可以定义 基本类型的响应式数据, 也可以定义对象类型响应式数据 <template><h1>{{ name }}</h1><button click"test">修改姓名</button> </template><script setup lang"ts"…...
ubuntu20.04设置共享文件夹
ubuntu20.04设置共享文件夹 一,简介二,操作步骤1,设置Windows下的共享目录2,挂载共享文件夹3,测试是否挂载成功 一,简介 在公司电脑上,使用samba设置共享文件夹,IT安全部门权限不通…...

三十五、 欧盟是如何对法律政策环境进行评估的?
我国对于如何评估数据接收方所在法律政策环境尚无明确详细的指引,故在实践中,为了进一步提升合规水平,企业也可同步参考在数据隐私保护法治方面领先的欧盟标准。 在欧盟法院于 2020 年 7 月作出 Schrems II案件的判决后,为保证境外…...
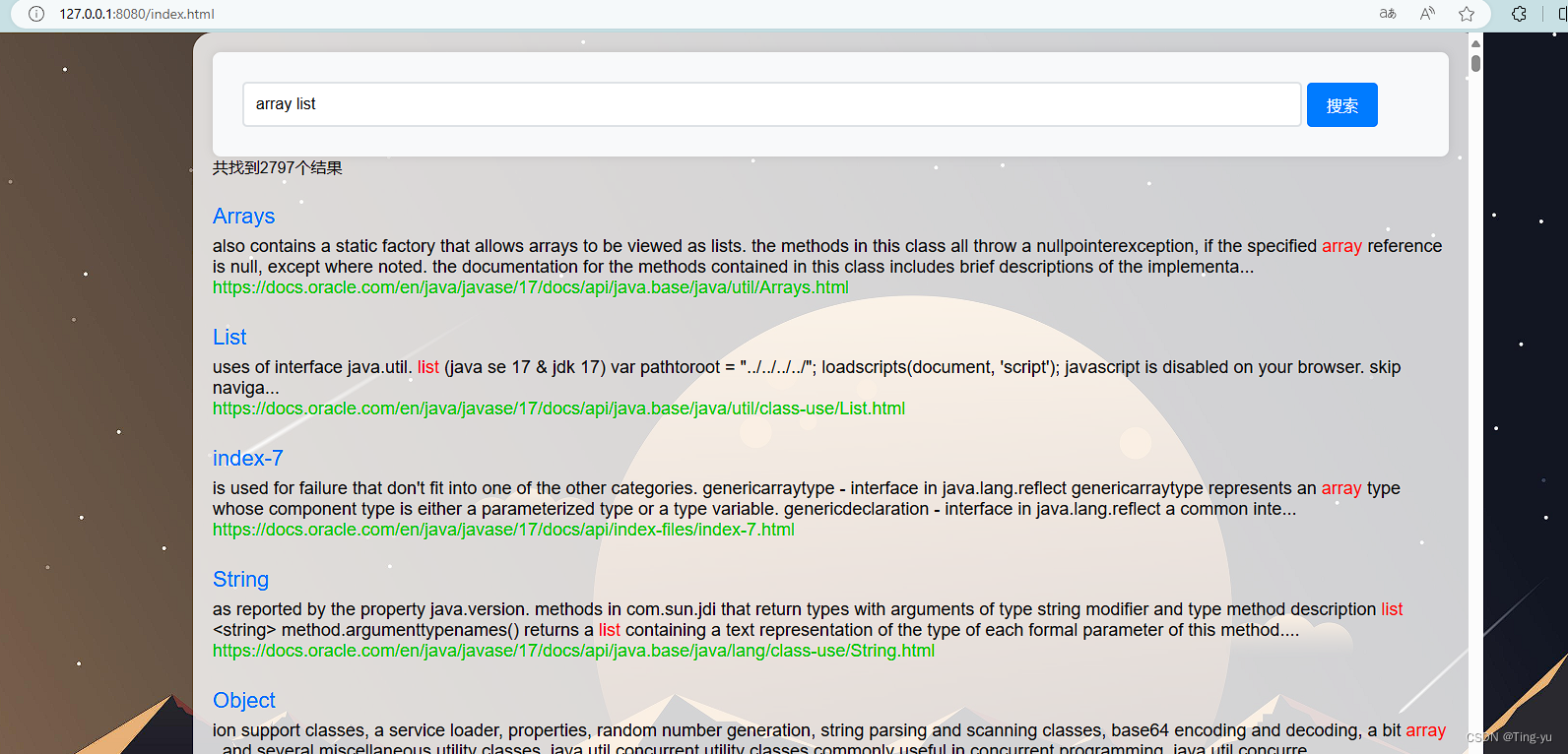
项目实战--文档搜索引擎
在我们的学习过程中,会阅读很多的文档,例如jdk的API文档,但是在这样的大型文档中,如果没有搜索功能,我们是很难找到我们想查阅的内容的,于是我们可以实现一个搜索引擎来帮助我们阅读文档。 1. 实现思路 1…...

计算机视觉基础课程知识点总结
图像滤波 相关: 核与图像同向应用,不翻转。 卷积: 核在应用前翻转,广泛用于信号处理和深度学习(现在常说的二维卷积就是相关)。 内积: 向量化的点积操作,是相关和卷积的一部分。 模板匹配:通过在图像中…...

编译原理:语法分析
目录 引言上下文无关文法 CFG: Context-Free Grammar定义推导方法最左推导和最右推导 分析树分析树->抽象语法树常见的上下文无关文法文法设计二义性文法扩展巴科斯范式:EBNF extended Backus Normal Form 文法和语言分类相关术语直接推导推导*推导句型、句子、语…...
React 中的 Lanes
React 中有一个 Lane 的概念,Lane 就像高速路上的不同车道,具有不同优先级,在 React Lane 通过一个 32 位的二进制数来表示。越小优先级别越高,SyncLane 级别最高。用二进制存储的方式,可以通过逻辑操作快速判断 Lane …...
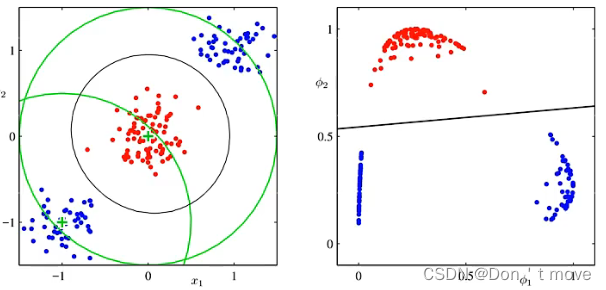
【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】线性分类模型损失函数对比
本节均以二分类问题为例进行展开,统一定义类别标签 y ∈ { 1 , − 1 } y\in\{1,-1\} y∈{1,−1},则分类正确时 y f ( x ; w ) > 0 yf(x;w)>0 yf(x;w)>0,且值越大越正确;错误时 y f ( x ; w ) < 0 yf(x;w)<0 yf(x;…...

数组(C语言)(详细过程!!!)
目录 数组的概念 一维数组 sizeof计算数组元素个数 二维数组 C99中的变⻓数组 数组的概念 数组是⼀组相同类型元素的集合。 数组分为⼀维数组和多维数组,多维数组⼀般比较多见的是二维数组。 从这个概念中我们就可以发现2个有价值的信息:(1)数…...

视频生成模型 Dream Machine 开放试用;微软将停止 Copilot GPTs丨 RTE 开发者日报 Vol.224
开发者朋友们大家好: 这里是 「RTE 开发者日报」 ,每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE(Real-Time Engagement) 领域内「有话题的 新闻 」、「有态度的 观点 」、「有意思的 数据 」、「有思考的 文…...
Vue30-自定义指令:对象式
一、需求:创建fbind指定 要用js代码实现自动获取焦点的功能! 二、实现 2-1、步骤一:绑定元素 2-2、步骤二:input元素获取焦点 此时,页面初始化的时候,input元素并没有获取焦点,点击按钮&…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
