C++算法-青蛙跳台阶【面试】
"青蛙跳台阶"问题是一个经典的递归问题,也与斐波那契数列有关。问题是这样的:一只青蛙站在一个n阶台阶上,它每次可以跳1阶或2阶,问青蛙跳到顶端总共有多少种跳法。
这个问题可以用递归或动态规划来解决。以下是使用C++实现的动态规划解法:
#include <iostream>
#include <vector>// 动态规划解法
int climbStairs(int n) {if (n <= 2) {return n;}// 创建一个数组来存储子问题的解std::vector<int> dp(n + 1, 0);// 初始化前两个台阶的跳法dp[1] = 1;dp[2] = 2;// 计算从3阶到n阶的跳法for (int i = 3; i <= n; ++i) {dp[i] = dp[i - 1] + dp[i - 2];}// 返回n阶台阶的跳法总数return dp[n];
}int main() {int n = 5;std::cout << "Number of ways to climb " << n << " steps is: " << climbStairs(n) << std::endl;return 0;
}
这段代码中,climbStairs函数使用了一个std::vector<int>来存储子问题的解,避免了重复计算。数组dp[i]表示到达第i阶台阶的跳法数。根据题目条件,到达第i阶台阶的跳法数等于到达(i-1)阶和(i-2)阶台阶的跳法数之和。
面试回答示例:
"青蛙跳台阶问题可以通过动态规划来解决。我们首先定义一个数组dp,其中dp[i]表示到达第i阶台阶的跳法数。我们知道到达第一阶和第二阶都只有一种方法。对于更高的台阶,到达那里的方法数是到达前一阶和前两阶台阶的方法数之和,因为青蛙可以选择从这两个位置跳过来。我们从第三阶台阶开始,逐步计算直到第n阶,最终返回dp[n]作为答案。这种方法避免了递归方法中的重复计算,时间复杂度是O(n),空间复杂度也是O(n)。"
相关文章:

C++算法-青蛙跳台阶【面试】
"青蛙跳台阶"问题是一个经典的递归问题,也与斐波那契数列有关。问题是这样的:一只青蛙站在一个n阶台阶上,它每次可以跳1阶或2阶,问青蛙跳到顶端总共有多少种跳法。 这个问题可以用递归或动态规划来解决。以下是使用C实…...
)
px转rem插件postcss-plugin-px2rem使用方法(浏览器缩放页面自适应)
px转rem插件postcss-plugin-px2rem使用方法(浏览器缩放页面自适应) 1. 常见屏幕自适应的布局 百分比布局rem布局css媒体查询在前端框架设计初期,应优先选择好页面布局方式 2. postcss-plugin-px2rem插件的使用 官网地址:https…...
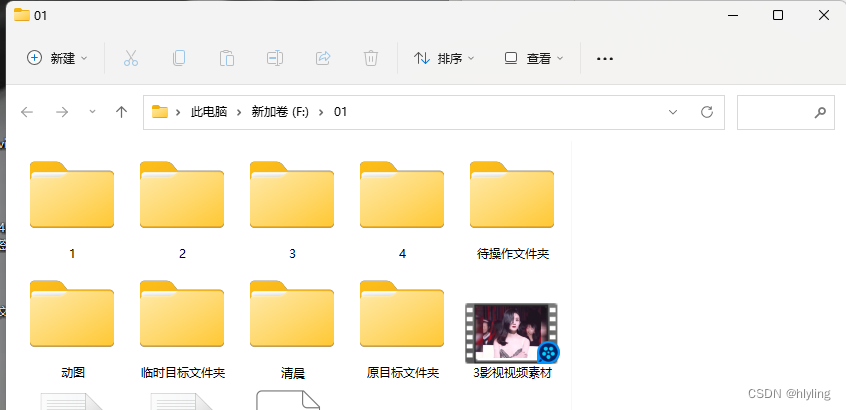
批量文件重命名技巧:轻松替换删除文件夹名中的字母,实现高效文件管理新境界
在数字化时代,我们每天都会面对大量的文件和文件夹。无论是工作文档、学习资料还是个人收藏,文件命名的规范性都显得尤为重要。然而,手动一个一个去修改文件名,不仅耗时耗力,还容易出错。那么,有没有一种方…...

windows设备/路由设备上ip地址如何查看、使用
在Windows设备上查看本地IP地址(IPv4和IPv6): 使用命令提示符: 打开命令提示符(在Windows中按Win R,然后输入"cmd"并按Enter)。在命令提示符窗口中,输入以下命令以查看…...

服务端⾼并发分布式结构演进之路
在进行技术学习过程中,由于大部分读者没有经历过一些中大型系统的实际经验,导致无法从全局理解一些概念,所以本文以一个"电子商务"应用为例,介绍从一百个到千万级并发情况下服务端的架构的演进过程,同时列举…...

Stable Diffusion ProtoVisionXL大模型之艺术盛宴!
今天基于ProtoVisionXL这款大模型为大家呈现一些视觉上的艺术盛宴,视觉冲击宣传海报信手拈来,再配上你的宣传语,妥妥地让人眼前一亮。 实测参数: 分辨率:768*1024 采样方法 (Sampler):DPM 2M Karras 迭代步数 (Ste…...
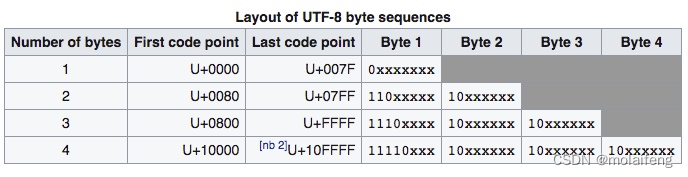
浅谈golang字符编码
1、 Golang 字符编码 Golang 的代码是由 Unicode 字符组成的,并由 Unicode 编码规范中的 UTF-8 编码格式进行编码并存储。 Unicode 是编码字符集,囊括了当今世界使用的全部语言和符号的字符。有三种编码形式:UTF-8,UTF-16&#…...

Vite和Webpack的区别是什么,你站队谁?
Vite和Webpack有很多相同之处,也有区别,很多老铁分不清,贝格前端工场借助此文为大家详细介绍一下。 一、关于Vite和Webpack Vite和Webpack都是前端开发中常用的构建工具,用于将源代码转换为可在浏览器中运行的静态资源。它们在一…...
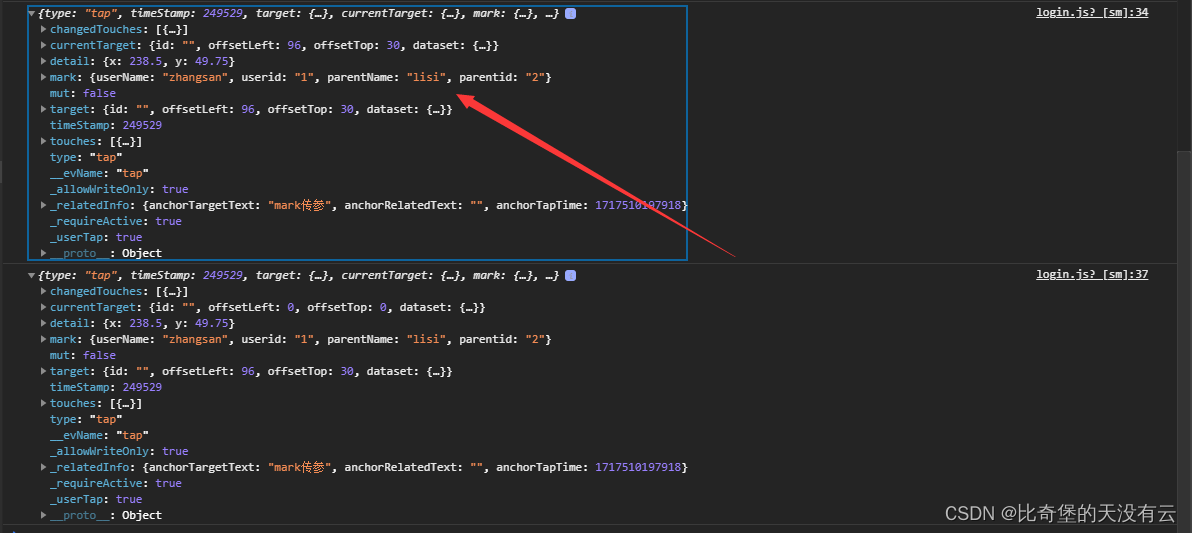
【微信小程序】事件传参的两种方式
文章目录 1.什么是事件传参2.data-*方式传参3.mark自定义数据 1.什么是事件传参 事件传参:在触发事件时,将一些数据作为参数传递给事件处理函数的过程,就是事件传参 在微信小程序中,我们经常会在组件上添加一些自定义数据,然后在…...

前端针对需要递增的固定数据
这里递增的是1到12 data(){return{cycleOptions:Array.from({ length: 12 }, (v, k) > ({value: k 1,label: String(k 1)})),} }<el-select v-model"ruleForm.monthLength" placeholder"请选择周期数量"><el-optionv-for"item in cycle…...

红酒保存中的氧气管理:适度接触与避免过度氧化
在保存云仓酒庄雷盛红酒的过程中,我们不得不面对一个微妙的问题:氧气管理。氧气,这个我们生活中无处不在的气体,对于红酒的保存却有着至关重要的影响。适度接触氧气对红酒的陈年过程和品质维护具有积极作用,然而过度氧…...

从零开始搭建开源智慧城市项目(三)上升线效果
前言 上一节实现了添加建筑物线框,模型外墙和道路地面材质添加。这一节准备通过简单的shader实现上升线效果。 思路 简单的说一下思路,通过获取模型顶点坐标所在的高度Z来进行筛选,高度再某一区间内设置成上升线的颜色,其余高度…...
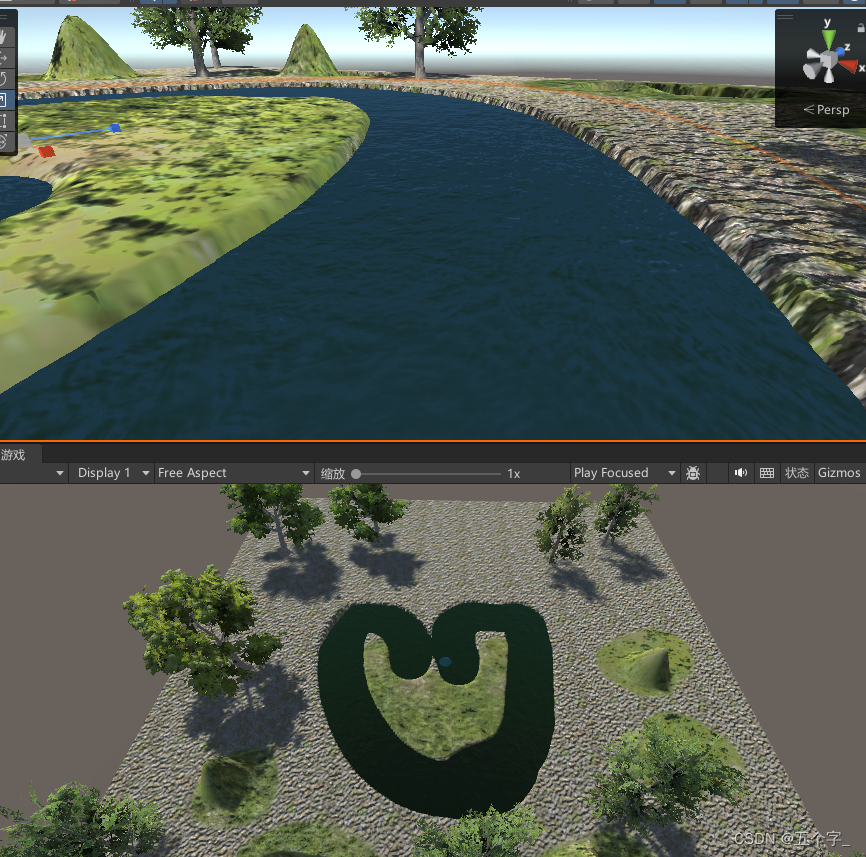
unity基础(五)地形详解
目录 一 创建地形 二 调整地形大小 三 创建相邻地形 四 创建山峰 五 创建树木 七 添加风 八 添加水 简介: Unity 中的基础地形是构建虚拟场景的重要元素之一。 它提供了一种直观且灵活的方式来创建各种地形地貌,如山脉、平原、山谷等。 通过 Unity 的地形…...

postman接口测试工具详解
Postman 是一个功能强大的 API 开发和测试工具,广泛应用于开发人员和测试人员进行 API 的调试、测试、文档生成等工作。以下是对 Postman 的详细介绍。 1. 功能概览 1.1 请求构建 请求类型: 支持 GET、POST、PUT、DELETE、PATCH、OPTIONS 等多种 HTTP 方法。URL …...
作者:————LJS)
2024年护网行动全国各地面试题汇总(3)作者:————LJS
应急响应基本思路和流程 收集信息:收集客户信息和中毒主机信息,包括样本判断类型:判断是否是安全事件,何种安全事件,勒索、挖矿、断网、DoS 等等抑制范围:隔离使受害⾯不继续扩⼤深入分析:日志分…...

计算机专业的学生要达到什么水平才能进入大厂工作?越早知道越好
计算机专业的学生要达到什么水平才能进入BAT等大厂工作?越早知道越好. 一、算法题 各大公司笔试、面试基本都考这个,别的不说,《剑指Offer》所有题目背下来,Leetcode高频题目刷个一两百遍,搞过ACM也可以,…...

巡检费时费力?试试AI自动巡检
随着企业IT规模不断增长,设备、系统越来越多,运维工作压力也与日俱增。保障设备、系统健康稳定地运行,日常巡检是运维工作不可或缺的部分。通过巡检可以及时发现设备、系统的异常问题,提前预防及时处理,避免问题扩大产…...

46-4 等级保护 - 网络安全等级保护概述
一、网络安全等级保护概述 原文:没有网络安全就没有国家安全 二、网络安全法 - 安全立法 中华人民共和国主席令 第五十三号 《中华人民共和国网络安全法》已于2016年11月7日由中华人民共和国第十二届全国人民代表大会常务委员会第二十四次会议通过,并自2017年6月1日起正式…...

css引入方式有几种?link和@import有什么区别?
在CSS中,引入外部样式表的方式主要有两种:<link>标签和import规则。 使用<link>标签引入外部样式表: <link rel"stylesheet" href"path/to/style.css">这种方式是在HTML文档的<head>部分或者…...

使用‘消除’技术绕过LLM的安全机制,不用训练就可以创建自己的nsfw模型
开源的大模型在理解和遵循指令方面都表现十分出色。但是这些模型都有审查的机制,在获得被认为是有害的输入的时候会拒绝执行指令,例如会返回“As an AI assistant, I cannot help you.”。这个安全功能对于防止误用至关重要,但它限制了模型的…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...
)
【系统架构设计师-2025上半年真题】综合知识-参考答案及部分详解(回忆版)
更多内容请见: 备考系统架构设计师-专栏介绍和目录 文章目录 【第1题】【第2题】【第3题】【第4题】【第5题】【第6题】【第7题】【第8题】【第9题】【第10题】【第11题】【第12题】【第13题】【第14题】【第15题】【第16题】【第17题】【第18题】【第19题】【第20~21题】【第…...
