【回溯】Leetcode 77. 组合【中等】
组合
- 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
解题思路
- 定义递归函数:定义一个递归函数 backtrack 用来生成组合。
- 递归终止条件:如果当前组合的长度达到 k,将其添加到结果列表中。
- 选择元素:从当前起始元素到 n 进行迭代,选择每个元素加入当前组合。
- 递归调用:选择元素后,递归调用函数生成下一个元素的组合。
- 回溯:在递归完成后,移除当前选择的元素,尝试选择下一个元素。
Java实现
public class Combine {public List<List<Integer>> combine(int n, int k) {List<List<Integer>> res = new ArrayList<>();backtrack(1, n, k, new ArrayList<>(), res);return res;}private void backtrack(int start, int n, int k, List<Integer> path, List<List<Integer>> res) {// 如果组合完成if (path.size() == k) {res.add(new ArrayList<>(path));return;}// 从`start`到`n`遍历所有的数字for (int i = start; i <= n; i++) {// 将`i`添加到当前组合path.add(i);// 使用下一个整数完成组合backtrack(i + 1, n, k, path, res);// 回溯,通过移除`i`path.remove(path.size() - 1);}}// 测试用例public static void main(String[] args) {Combine solution = new Combine();System.out.println(solution.combine(4, 2)); // 期望输出: [[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]System.out.println(solution.combine(5, 3)); // 期望输出: [[1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]}
}时间空间复杂度
- 时间复杂度:O(C(n, k) * k),其中 C(n, k) 是从 n 个数中选 k 个数的组合数。生成每个组合需要 O(k) 的时间。
- 空间复杂度:O(k),递归栈的深度最多为 k,存储当前组合的路径 path 也需要 O(k) 的空间。
相关文章:

【回溯】Leetcode 77. 组合【中等】
组合 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 示例 1: 输入: n 4, k 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ] 解题思路 定义递归函数࿱…...

项目中常量的定义方式
方式一 在常量个数少的时候,通常情况下使用这种方式。 public class MqConstants {public static final String EXCHANGE_1 "exchange1";public static final String EXCHANGE_2 "exchange2";public static final String EXCHANGE_3 "…...
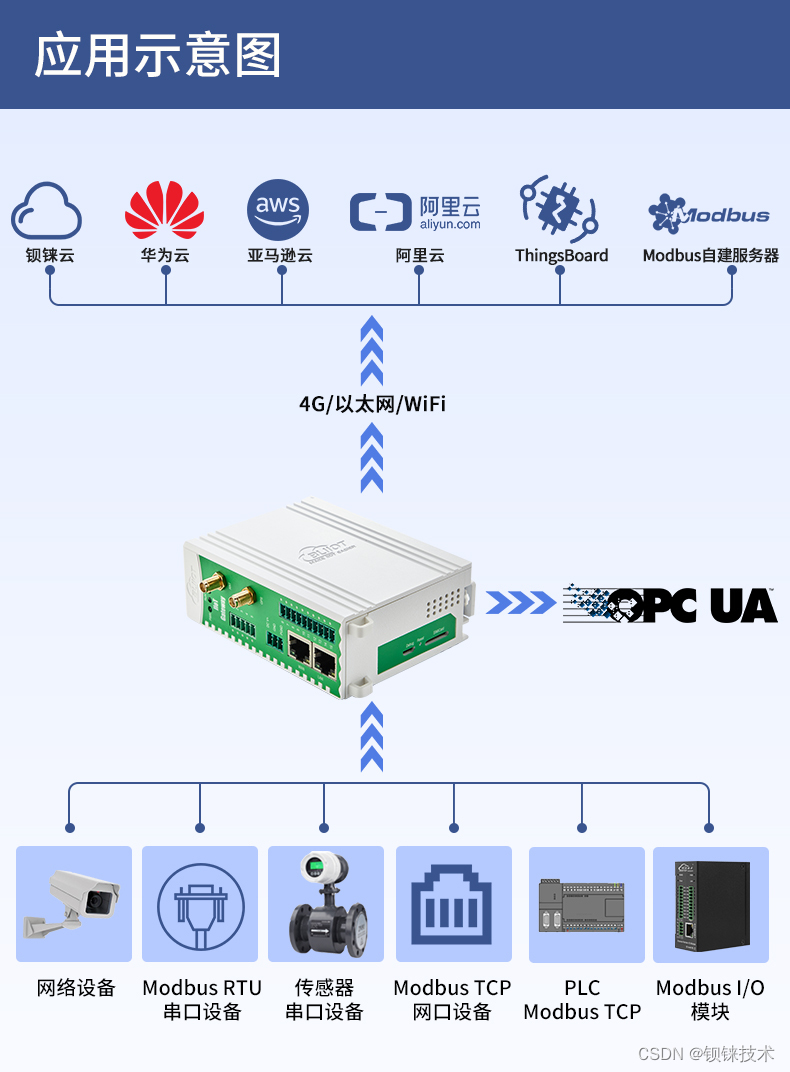
BL104钡铼多协议采集网关助力企业智能化转型
BL104钡铼多协议采集网关(PLC物联网关BL104)是为满足工业环境需求而设计的专业工业级协议转换网关。它在企业智能化转型过程中扮演着关键角色,为企业提供了高效、稳定的通信解决方案,助力企业实现智能化转型。 首先,P…...

【LC刷题】DAY08:151 55 28 459
【LC刷题】DAY08:151 55 28 459 文章目录 【LC刷题】DAY08:151 55 28 459151. 反转字符串中的单词 [link](https://leetcode.cn/problems/reverse-words-in-a-string/description/)55. 右旋字符串 [link](https://kamacoder.com/problempage.php?pid106…...

Debian 12.5 一键安装 Oracle 19C 单机
前言 Oracle 一键安装脚本,演示华为 Debian 12.5 一键安装 Oracle 19C 单机版过程(全程无需人工干预)。 ⭐️ 脚本下载地址:Shell脚本安装Oracle数据库 安装准备 1、安装好操作系统,建议安装图形化2、配置好网络3、上…...

ARP协议相关
把ip地址解析成mac地址这里的mac地址就是路由器的mac地址 免费ARP 源ip和目的ip都是一样的,那怎么让其他人更新arp表呢?? 是因为目标mac是全f,是一个广播报文 如果冲突就是ip一样但是mac又不一样 代理ARP pc1和pc4是在同一个子网…...

Github 2024-06-14 开源项目日报Top10
根据Github Trendings的统计,今日(2024-06-14统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量JavaScript项目2Python项目2非开发语言项目2TypeScript项目1Dart项目1Rust项目1Lua项目1Java项目1Jupyter Notebook项目1从零开始构建你喜爱的技…...
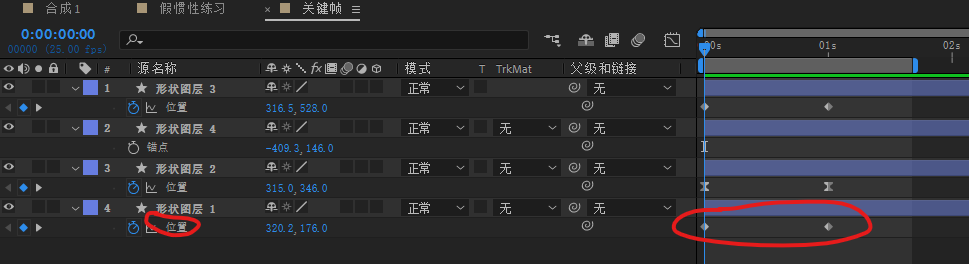
记录AE快捷键(持续补充中。。。)
记录AE快捷键 快捷键常用快捷键图层快捷键工具栏图层与属性常用指令视图菜单时间轴常规快捷键项目首选项功能摄像机操作 常用操作导入AI/PS工程文件加选一个关键参数快速回到上下一帧隐藏/显示图层关键帧拉长缩短关键帧按着鼠标左键不松手,在秒表那一列往下移动会都…...

基于springboot实现问卷调查系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现问卷调查系统演示 摘要 传统信息的管理大部分依赖于管理人员的手工登记与管理,然而,随着近些年信息技术的迅猛发展,让许多比较老套的信息管理模式进行了更新迭代,问卷信息因为其管理内容繁杂,管理数…...

React@16.x(29)useRef
目录 1,介绍2,和 React.createRef() 的区别3,计时器的问题 目前来说,因为函数组件每次触发更新时,都会重新运行。无法像类组件一样让一些内容保持不变。 所以才出现了各种 HOOK 函数:useState,u…...

无人机的力量——在民用方面的应用
无人机在民用方面的应用广泛且多样化,以下是对其应用的详细介绍: 影视航拍: 无人机航拍影像具有高清晰、大比例尺、小面积、高视角的优点,特别适合获取带状地区航拍影像(如公路、铁路、河流、水库、海岸线等ÿ…...

探索档案未来,尽在ARCHE-2024
2024年第三届上海国际智慧档案展览会暨高峰论坛(ARCHE-2024)将于2024年6月19日至21日在上海跨国采购会展中心隆重举行。深圳市铨顺宏科技有限公司应邀参展,将以全新形象盛装亮相,展示其在档案管理领域的最新技术和解决方案。 ARC…...

Maven 核心插件 maven-clean-plugin 使用详解
在软件开发中,构建和管理项目的复杂性随着代码量和依赖的增加而不断提升。Maven作为一个强大的构建工具,简化了这一过程,并通过其插件机制提供了丰富的功能。其中,maven-clean-plugin 是Maven的核心插件之一,它在项目的…...
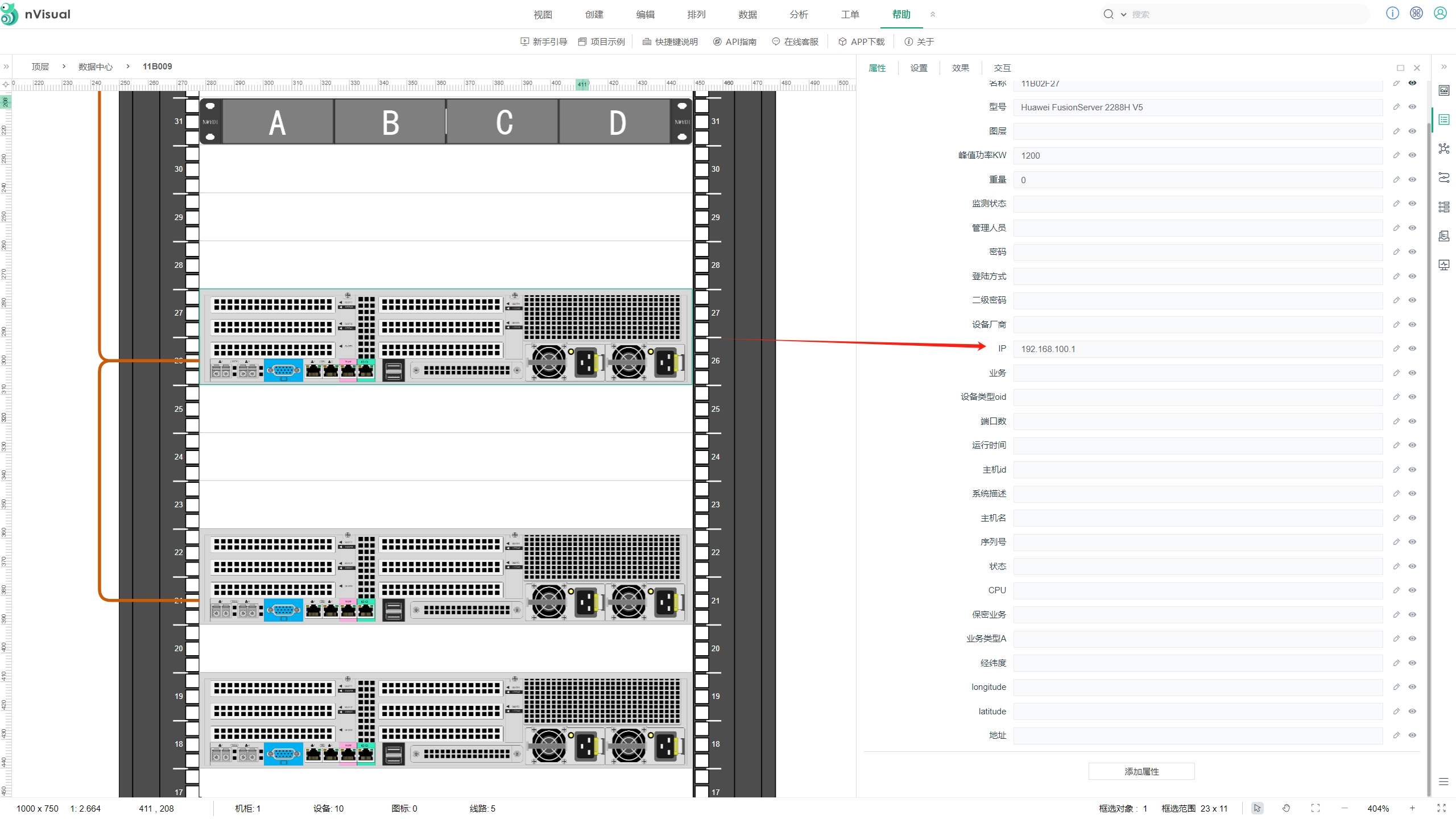
金融数据中心布线运维管理解决方案
金融行业的核心业务,如交易、支付、结算等,对网络的依赖程度极高。布线作为网络基础设施的重要组成部分,其稳定性和可靠性直接关系到业务的连续运行。因此,良好的布线管理能够确保网络系统的稳定运行,减少因网络故障导…...

C++初学者指南第一步---2. Hello world
C初学者指南第一步—2. Hello world 目录 C初学者指南第一步---2. Hello world1.源文件 “Hello.cpp”2.编译hello.cpp3.术语4.编译器标志5.不要使用 “using namespace std;” ! 1.源文件 “Hello.cpp” #include <iostream> // our first program int main…...
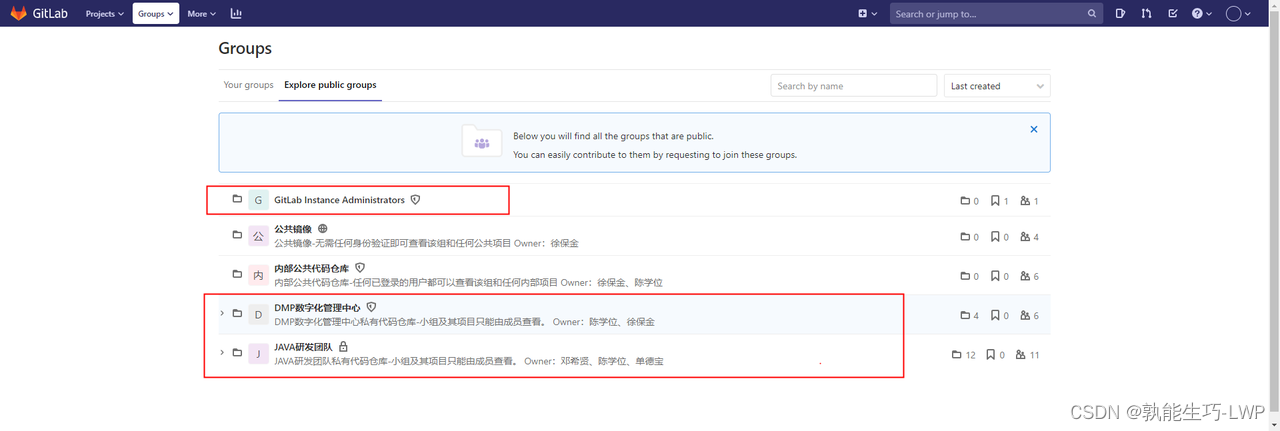
gitLab批量下载有权限的项目
前言 参考 https://www.jianshu.com/p/b3d4e5cee835 适用于git私服拉取个人所涉及权限的代码,方便有多个项目权限的人快速拉取自己所有权限的代码。 默认生成目录结构与gitlab一致 步骤一:获取权限你的代码权限文件d 从gitlab私服生成所有你有权限的代码信息 …...

解决 kali 中使用 vulhub 拉取不到镜像问题
由于默认情况下,访问的镜像是国外的,而从 2023 年开始,docker 的镜像网站就一直访问不了,所以我们可以把镜像地址改成国内的阿里云镜像地址。 1、在 cd /etc/docker/目录下创建或修改daemon.json文件 sudo touch daemon.json 2、在…...

CSS3 简介
CSS3 简介 CSS3,即层叠样式表的第三代,是网页设计和开发中不可或缺的技术之一。它为HTML元素提供了更加丰富和灵活的样式定义,使得网页不仅结构清晰,而且外观精美、交互性强。CSS3继承了CSS2的基本特性,并引入了许多新…...

springboot事务管理的机制是什么
SpringBoot的事务管理机制实质上是基于Spring框架的事务处理机制。其主要目的是确保一系列数据库操作要么全部成功,要么全部失败(回滚),从而维护数据的完整性和一致性。 SpringBoot事务管理遵循ACID四大特性: 1、原子…...

Linux下tar命令解压缩
tar 命令是 Unix 和 Linux 系统中用来创建归档文件以及提取归档文件的工具。它通常用于备份文件或将多个文件和目录打包成一个单独的归档文件。默认情况下,tar 不会对文件进行压缩,但可以通过结合其他压缩工具(如 gzip 或 bzip2)来…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
