Codeforces Round 953 (Div. 2)(A~D题解)
这次比赛是我最顺利的一次比赛,也是成功在中途打进前1500,写完第三道题的时候也是保持在1600左右,但是后面就啥都不会了,还吃了点罚时,虽说如此也算是看到进步了,D题学长说很简单,但是我当时分析错了,出了一点小问题,不然最后也能定格在2000左右,下次加油。
A. Alice and Books


题意:就是说给你n本书,让你从中间分开,阅读边编号最大的那本书,然后问你最多能读多少页,这个很简单,最后一本书肯定是要读的,我们只需要遍历从1到~n-1本书,找到那本书页数最多然后加起来就OK了
#include<bits/stdc++.h>
using namespace std;
#define int long longint t;
int n;
int a[105];
int maxn=0;
signed main()
{cin>>t;while(t--){maxn=0;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n-1;i++){maxn=max(maxn,a[i]);}cout<<maxn+a[n]<<"\n";}return 0;
}B. New Bakery


题意:就是说给你n个面包,每个面包有两种卖价,一个是a元,一个是b元,b元的计算是
(b-i+1)也就是说越往后卖b价越低
思路:既然b价格越来越低,那么等b的价格和a一样的时候就按a的价格卖即可,因此我们一开始做出判断如果a>b那就全按a的价格来卖,如果a<b,那么等b的价格低到和a一样的时候就按a元来卖就有最大价值
ps:同时要注意 b是否真的会低到a的价格
#include<bits/stdc++.h>
using namespace std;
#define int long long
int t;
int n;
int a,b;
signed main()
{cin>>t;while(t--){cin>>n>>a>>b;if(a>=b){cout<<a*n<<"\n";}else{int sum=0;int flag=b-a;if(n>flag){sum=(a+1+b)*(b-a)/2+(n-flag)*a;}else{sum=(b+b-n+1)*n/2;}cout<<sum<<"\n";}}return 0;
}C. Manhattan Permutations

题意:就是给你一个数组,数组的数值是1~n,然后问你其中产生的曼哈顿值是否能达到k
思路:我们首先要判断哪些情况下不会达到,首先就是因为你是交换产生的曼哈顿值,曼哈顿值一但产生就必然是偶数,而不可能是奇数,当k为奇数时直接输出NO即可
其次就是当整个序列反转的时候产生最大的曼哈顿值,因而假如我们的k要是大于反转之后的曼哈顿值也要输出NO
然后就是很简单的根据k去进行翻转就好,我们要对k的值进行判断,我们要从第一个数开始交换,然后每次交换都是要根据k值的大小去交换的(这个地方不会的直接私我吧,文学功底有限,实在太难纯文本将清楚了)
#include<bits/stdc++.h>
using namespace std;
#define int long longint t;
int n,k;
int maxn;//用于计算最大差值
int a[200005];
signed main()
{cin>>t;while(t--){cin>>n>>k;for(int i=1;i<=n;i++)a[i]=i;if(k%2!=0){cout<<"NO\n";continue;}maxn = 0; for(int i=1;i<=n;i++){maxn+=abs(n-i+1-i);}if(maxn<k){cout<<"NO\n";continue;}int flag=2*(n-1);int num=1;while(k!=0){if(k>=flag){
// cout<<flag<<"\n";
// cout<<a[num]<<" "<<a[n-num+1]<<"flag\n";int t=a[num];a[num]=a[n-num+1];a[n-num+1]=t;k-=flag;num++;flag=2*(n-num+1-num);}else{int cnt=k/2;int t=a[num];a[num]=a[num+cnt];a[num+cnt]=t;k=0;}}cout<<"YES\n";for(int i=1;i<=n;i++){cout<<a[i]<<" ";}cout<<"\n";}return 0;
}D. Elections


题意:就是说有n个候选人,c个无主见人士,无主见的人会将票投给下标最小的那个的人,然后问你想要让第i个当选,要排除最少多少个竞争者
思路:我们需要去对于
(1)第一个要特判,如果第一个加上未决定的票数就可以大于最多的,那么第一个人不用将任何候选人排除
(2)如果我票数就是最多的且我的下标小的话也可以在同票数的情况下获胜,并且第一个人+c个人的票也无法超过我,因此,也不需要排除别人
(3)其余的需要判断其是否比最大值那个下标小,或者说把前面的都筛掉之后+c能否大于最多那个人得票数,如果这两个条件满足其一,就输出i-1即可
#include <bits/stdc++.h>
using namespace std;
#define int long long
int t;
int n,c;
int a[200005];
int pre[200005];
bool cmp(pair<int,int> a, pair<int,int> b)
{if(a.first==b.first) return a.second>b.second;return a.first<b.first;
}
void solve()
{cin >> n >> c;vector<pair<int,int>> b(n+1);b[0]={0,0};for(int i=1;i<=n;i++){cin >> a[i];b[i]={a[i],i};}sort(b.begin(),b.end(), cmp);for(int i=1;i<=n;i++){pre[i]=pre[i-1]+b[i].first;}int sum=0;for(int i=1;i<=n;i++){if(i==1 && a[i]+c>=b[n].first){cout << 0 << ' '; }else if(((a[i]==b[n].first && i<=b[n].second)) && a[1]+c<a[i]){cout << 0 << ' ';}else{cout << i-(b[n].second<=i || sum+a[i]+c>=b[n].first)<<' ';}sum+=a[i];}cout << "\n";
}
signed main()
{cin >> t;while(t--){solve();}return 0;
}相关文章:

Codeforces Round 953 (Div. 2)(A~D题解)
这次比赛是我最顺利的一次比赛,也是成功在中途打进前1500,写完第三道题的时候也是保持在1600左右,但是后面就啥都不会了,还吃了点罚时,虽说如此也算是看到进步了,D题学长说很简单,但是我当时分析…...

晶圆切割机(晶圆划片机)为晶圆加工重要设备 我国市场国产化进程不断加快
晶圆切割机(晶圆划片机)为晶圆加工重要设备 我国市场国产化进程不断加快 晶圆切割机又称晶圆划片机,指能将晶圆切割成芯片的机器设备。晶圆切割机需具备切割精度高、切割速度快、操作便捷、稳定性好等特点,在半导体制造领域应用广…...
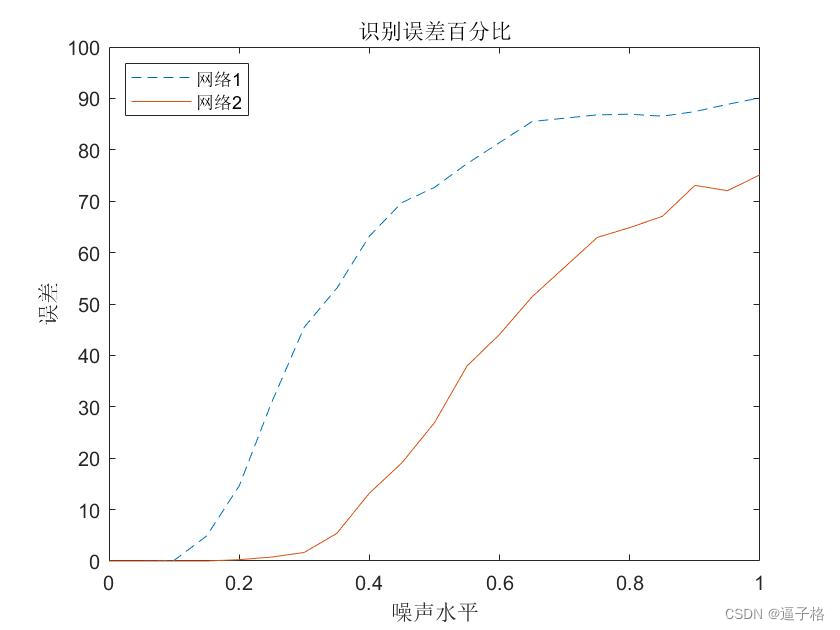
39、基于深度学习的(拼音)字符识别(matlab)
1、原理及流程 深度学习中常用的字符识别方法包括卷积神经网络(CNN)和循环神经网络(RNN)。 数据准备:首先需要准备包含字符的数据集,通常是手写字符、印刷字符或者印刷字体数据集。 数据预处理࿱…...

CCF 矩阵重塑
第一题:矩阵重塑(一) 本题有两种思路 第一种 (不确定是否正确 但是100分) #include<iostream> using namespace std; int main(){int n,m,p,q,i,j;cin>>n>>m>>p>>q;int a[n][m];for(i…...

Aigtek高压放大器在柔性爬行机器人驱动性能研究中的应用
实验名称:柔性爬行机器人的材料测试 研究方向:介电弹性体的最小能量结构是一种利用DE材料的电致变形与柔性框架形变相结合设计的新型柔性驱动器,所谓最小能量是指驱动器在平衡状态时整个系统的能量最小,当系统在外界的电压刺激下就…...

Postman下发流表至Opendaylight
目录 任务目的 任务内容 实验原理 实验环境 实验过程 1、打开ODL控制器 2、网页端打开ODL控制页面 3、创建拓扑 4、Postman中查看交换机的信息 5、L2层流表下发 6、L3层流表下发 7、L4层流表下发 任务目的 1、掌握OpenFlow流表相关知识,理解SDN网络中L…...

C语言王国——数组的旋转(轮转数组)三种解法
目录 一、题目 二、分析 2.1 暴力求解法 2.2 找规律 2.3 追求时间效率,以空间换时间 三、结论 一、题目 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出…...

MySQL中CAST和CONVERT函数都用于数据类型转换
在 MySQL 中,CAST() 和 CONVERT() 函数都用于数据类型转换。虽然这两个函数在大多数情况下可以互换使用,但它们之间还是有一些细微的差别。 官方文档地址 https://dev.mysql.com/doc/refman/8.4/en/cast-functions.html#function_cast CAST() 函数 C…...

速盾:cdn影响seo吗?
CDN (Content Delivery Network) 是一个分布式网络架构,用于在全球范围内加速网站内容的传输和分发。它通过将网站的静态资源(例如图片、CSS、JavaScript 文件等)存储在多个服务器上,使用户可以从最接近他们位置的服务器上获取这些…...
期末算法复习
0-1背包问题(动态规划) 例题 算法思想: 动态规划的核心思想是将原问题拆分成若干个子问题,并利用已解决的子问题的解来求解更大规模的问题。 主要是状态转移方程和状态 算法描述: 初始化一个二维数组dp࿰…...

可穿戴设备:苹果“吃老底”、华为“忙复苏”、小米“再扩容”
配图来自Canva可画 随着产品功能的创新,可穿戴设备不再被简单地视为手机的延伸,而是被当成一种独立的、具有独特功能和优势的产品,受到了越来越多人的青睐。 一方面,技术的进步使得可穿戴设备在功能、性能和使用体验上得到显著提…...

AI数据分析:集中度分析和离散度分析
在deepseek中输入提示词: 你是一个Python编程专家,要完成一个Python脚本编写的任务,具体步骤如下: 读取Excel表格:"F:\AI自媒体内容\AI行业数据分析\toolify月榜\toolify2023年-2024年月排行榜汇总数据.xlsx&qu…...

redis的分布式session和本地的session有啥区别
在web应用开发中,Session用于在多个请求之间存储用户数据。传统上,Session存储在服务器的内存中,即本地Session。然而,随着应用规模和复杂度的增加,特别是在分布式环境中,本地Session会遇到一些问题。这时&…...

SSH概念、用途、详细使用方法
还是大剑师兰特:曾是美国某知名大学计算机专业研究生,现为航空航海领域高级前端工程师;CSDN知名博主,GIS领域优质创作者,深耕openlayers、leaflet、mapbox、cesium,canvas,webgl,ech…...
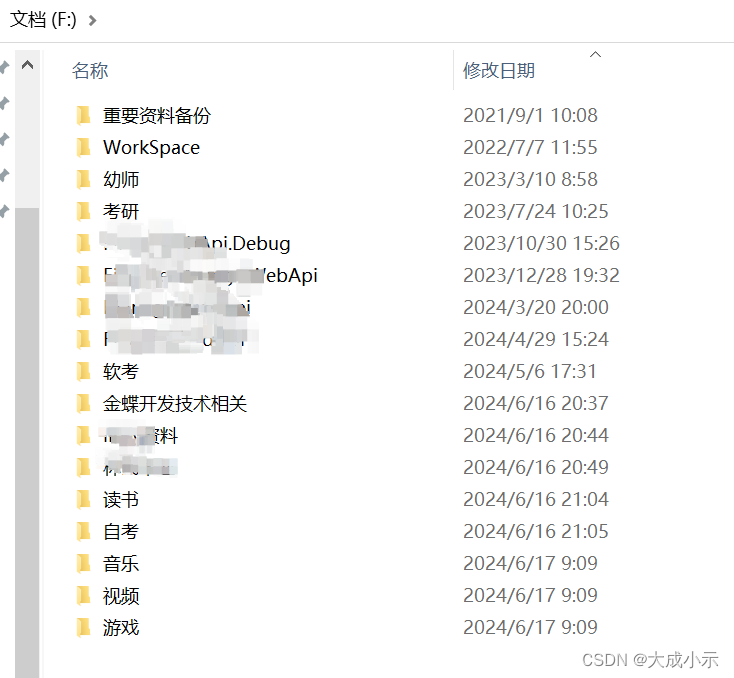
关于电脑文件的规划思考
概述 设置C、D、E、F 四个盘 C盘:系统数据使用,操作系统、其他软件需要用到的系统性资源 D盘:应用软件区 的使用,数据库、navacat、idea、visual studio、浏览器、向日葵、虚拟机…… E盘:工作区:公司资料…...
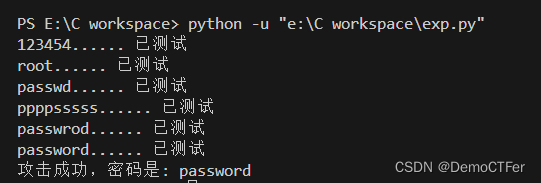
DVWA - Brute Force
DVWA - Brute Force 等级:low 直接上bp弱口令爆破,设置变量,攻击类型最后一个,payload为用户名、密码简单列表 直接run,长度排序下,不一样的就是正确的用户名和密码 另解: 看一下…...
安卓手机文件找回方法汇总,3个技巧,不再焦虑
我们用手机来储存各种重要的信息和文件,无论是珍贵的照片、重要的文档还是喜爱的音乐,用来记录和分享生活中的每一个瞬间。但如果不小心删除了这些文件,我们可能会面临数据丢失的风险,进而产生焦虑和不安。本文将为您揭秘手机文件…...

{}初始化
文章目录 ()初始化的问题易混淆弱检查 {}初始化{}初始化是c11推荐的初始化,解决了上述的问题 ()则被用于强制类型转换 ()初始化的问题 易混淆 string s();不能确定是函数定义还是对象定义 弱检查 int a(3.14);3.14 可以通过 int 定义 {}初始化 {}初始化是c11推…...

小程序外卖开发中的关键技术与实现方法
小程序外卖服务凭借其便捷性和灵活性,正成为现代餐饮行业的重要组成部分。开发一个功能完善的小程序外卖系统,需要掌握一系列关键技术和实现方法。本文将介绍小程序外卖开发中的核心技术,并提供具体的代码示例,帮助开发者理解和实…...

大数据平台之运维管理工具
大数据平台的自动化运维管理工具能够大幅提升集群管理效率,减少人为错误,提高系统的稳定性和性能。这些工具通常提供集群监控、配置管理、自动化任务执行、安全管理和故障处理等功能。以下是一些主要的大数据平台自动化运维管理工具的详细介绍࿱…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
