⭐ ▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch3 贝尔曼最优公式 【压缩映射定理】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍
- 1、视频 + 学堂在线 习题
- 2、过 电子书,补充 【下载:本章 PDF 电子书 GitHub 界面链接】 [又看了一遍视频]
- 3、总体 MOOC 过一遍 习题
学堂在线 课程页面链接
中国大学MOOC 课程页面链接
B 站 视频链接
PPT和书籍下载网址: 【GitHub 链接】
强化学习的最终目标: 寻求最优策略
贝尔曼最优公式, 可以求解 最优状态值 和 最优策略。

————————
P1 如何 改进策略 ——> 选择 动作值 最大的动作
最优状态值、最优策略
the Bellman optimality equation (BOE) 贝尔曼最优公式

计算 状态值 v π ( s ) v_\pi(s) vπ(s), 然后计算 动作值 q π ( s ) q_\pi(s) qπ(s)
选择 动作值 最大的动作可以得到 比较好的策略 。
选择 动作值 大的策略, 不断迭代, 一定可以得到 最优策略。
——————
P2 最优策略 定义
用 状态值 来评估一个策略的好坏:
若 对于 所有的 s ∈ S s\in \mathcal S s∈S, 均满足 v π 1 ( s ) ≥ v π 2 ( s ) v_{\pi_1}(s)\geq v_{\pi_2}(s) vπ1(s)≥vπ2(s)。 则认为 策略 1 比 策略 2 好。
最优策略 π ∗ \pi^* π∗: 对 所有 s s s 和 所有策略 π \pi π, 均有 v π ∗ ( s ) ≥ v π ( s ) v_{\pi^*}(s) \geq v_\pi(s) vπ∗(s)≥vπ(s)。
与所有其他策略相比,最优策略在每个状态下都具有最大的状态值。
最优策略是否一定存在?
最优策略是唯一的吗?
最优策略是随机的还是确定的?
如何获得最优策略?
在后续内容中,需要 求解 形如 f ( v ) = v f(v) = v f(v)=v 的方程,这正是 压缩映射定理【不动点定理】的相关内容。可证得 最优策略 对应的最优状态值 存在且唯一。
3.3 贝尔曼最优公式
v ( s ) = max π ∑ a π ( a ∣ s ) ( ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v ( s ′ ) ) , ∀ s ∈ S = max π ∑ a π ( a ∣ s ) q ( s , a ) , s ∈ S \begin{aligned}v(s)&= \textcolor{blue}{\max\limits_\pi}\sum\limits_a\pi(a|s)\Big(\sum\limits_rp(r|s,a)r+\gamma \sum\limits_{s^\prime}p(s^\prime|s, a)v(s^\prime)\Big), ~~~~\forall s\in\mathcal S\\ &=\max\limits_\pi\sum\limits_a\pi(a|s)q(s, a), ~~~s\in\mathcal S\end{aligned} v(s)=πmaxa∑π(a∣s)(r∑p(r∣s,a)r+γs′∑p(s′∣s,a)v(s′)), ∀s∈S=πmaxa∑π(a∣s)q(s,a), s∈S
通过求解这个方程, 可以获得 最优策略 和 最优状态值。
- 已知: p ( r ∣ s , a ) , p ( s ′ ∣ s , a ) p(r|s,a),~~~p(s^\prime|s,a) p(r∣s,a), p(s′∣s,a)
- 未知: v ( s ) , v ( s ′ ) v(s),~~~v(s^\prime) v(s), v(s′)
$\forall$ ∀ ~~\forall ∀
贝尔曼最优方程的 矩阵-向量形式:
v = max π ( r π + γ P π v ) \bm v=\max \limits_\pi(\bm r_\pi+\gamma\bm P_\pi\bm v) v=πmax(rπ+γPπv)
- [ r π ] s ≜ ∑ a π ( a ∣ s ) ∑ r p ( r ∣ s , a ) r [r_\pi]_s\triangleq\sum\limits_a\pi(a|s)\sum\limits_rp(r|s, a)r [rπ]s≜a∑π(a∣s)r∑p(r∣s,a)r
- [ P π ] s , s ′ = p ( s ′ ∣ s ) ≜ ∑ a π ( a ∣ s ) ∑ s ′ p ( s ′ ∣ s , a ) [P_\pi]_{s,s^\prime}=p(s^{\prime}|s)\triangleq\sum\limits_a\pi(a|s)\sum\limits_{s^\prime}p(s^{\prime}|s, a) [Pπ]s,s′=p(s′∣s)≜a∑π(a∣s)s′∑p(s′∣s,a)
$\triangleq$ ≜ ~~\triangleq ≜
如何求解这个方程?
存在性:这个方程有解吗?
唯一性:这个方程的解是否唯一?
最优性:这个解与最优策略有什么关系?
一个式子, 两个未知量。如何求解 右侧的最大化?


类似地, 求解 贝尔曼最优方程
v ( s ) = max π ∑ a π ( a ∣ s ) q ( s , a ) v(s)=\max\limits_\pi\sum\limits_a\pi(a|s)q(s, a) v(s)=πmaxa∑π(a∣s)q(s,a)
受上述例子启发, 由于 ∑ a π ( a ∣ s ) = 1 \sum\limits_a\pi(a|s)=1 a∑π(a∣s)=1
∑ a π ( a ∣ s ) q ( s , a ) ≤ ∑ a π ( a ∣ s ) max a q ( s , a ) = max a q ( s , a ) \sum\limits_a\pi(a|s)q(s, a)\leq\sum\limits_a\pi(a|s)\max\limits_aq(s,a)=\max\limits_aq(s, a) a∑π(a∣s)q(s,a)≤a∑π(a∣s)amaxq(s,a)=amaxq(s,a)
∑ a π ( a ∣ s ) q ( s , a ) \sum\limits_a\pi(a|s)q(s, a) a∑π(a∣s)q(s,a) 是类似于 上述例子中的求和式,根据经验,让取得最大的 q ( s , a ) q(s, a) q(s,a) 【相当于 q 3 q_3 q3】相应的概率 π ( a ∣ s ) \pi(a|s) π(a∣s) 【相当于 c 3 c_3 c3】为 1, 其它情况相应的 π ( a ∣ s ) \pi(a|s) π(a∣s) 为 0, 此时能获得最大值
即 令 π ( a ∣ s ) = { 1 , a = a ∗ 0 , a ≠ a ∗ \pi(a|s)=\left\{ \begin{aligned} &1, &a=a^*\\ &0, &a\neq a^*\\ \end{aligned} \right. π(a∣s)={1,0,a=a∗a=a∗
- a ∗ a^* a∗:最大的 q q q 值对应的 action。 a ∗ = arg max a q ( s , a ) a^*=\arg \max\limits_aq(s, a) a∗=argamaxq(s,a)
最优策略 π ( s ) π(s) π(s) 是选择具有 最大 q ( s , a ) q(s, a) q(s,a) 的动作的策略。
——————
3.3.3 压缩映射定理 : 求解 v = f(v)
P3
压缩映射定理 是分析一般非线性方程的有力工具。它也被称为不动点定理。

回到正题:

令 f ( v ) = max π ( r π + γ P π v ) f(\bm v)=\max\limits_\pi(\bm r_\pi+\gamma\bm P_\pi\bm v) f(v)=πmax(rπ+γPπv)
v = f ( v ) ~~\bm v=f(\bm v) v=f(v)

映射后的距离 比 之前 小。
示例:



该定理描述了 不动点 和 压缩映射 之间的关系
只要是 具有 形如 x = f ( x ) x = f(x) x=f(x) 的压缩映射, 必存在 一个 不动点 满足 f ( x ∗ ) = x ∗ f(x^*)=x^* f(x∗)=x∗ ,且这个不动点是 唯一的。可通过 迭代式 x k + 1 = f ( x k ) x_{k+1}=f(x_k) xk+1=f(xk) 求解。
压缩映射定理不仅可以判断非线性方程的解是否存在,而且还提供了求解该方程的数值算法。
P53-
- 证明 1: 压缩映射定理 P53- [见 后文补充]
如何利用 压缩映射定理 提出的 迭代算法 计算一些方程的不动点
例子:

3.3.4 贝尔曼最优公式的右侧 具有 压缩性
为了 应用 上述的 压缩映射定理 求解 贝尔曼最优方程 , 需要 证明 f ( v ) f(v) f(v) 是具有 收缩 的性质。


- 证明 2: 贝尔曼最优方程 的右侧 是 压缩映射的 P55- [ 见 后文补充]
3.4 贝尔曼最优方程 的解
上述 内容 证明了 贝尔曼最优方程 可以 运用 压缩映射定理 进行分析,可通过 迭代式 求解。


最优策略 π ∗ = arg max π ( r π + γ P π v ∗ ) \pi^*=\arg\max\limits_\pi(r_\pi+\gamma P_\pi v^*) π∗=argπmax(rπ+γPπv∗)
v ∗ v^* v∗ 是不动点, 因为 v ∗ = f ( v ∗ ) v^*=f(v^*) v∗=f(v∗)。
贝尔曼最优公式 是 策略为最佳策略时的贝尔曼公式。
这个策略 是不是 最优的 ?
状态值 v π ∗ v_{\pi^*} vπ∗ 是不是 最大的 ?
贝尔曼最优公式的不动点解 【最终的收敛值】 v ∗ v^* v∗ 就是 最大的状态值,此时的 π ∗ \pi^* π∗ 为最优策略。 [因为 对应的状态值最大]

BOE: 描述了 最优状态值 和 最优策略。
- 证明 3: 贝尔曼最优方程的解对应 最大状态值 和 最优策略 P58- [见 后文补充]
最优策略 π ∗ \pi^* π∗ 长 啥样呢?

总存在一个确定性的最优贪婪策略。

同样是类似于之前的求和式,令 q ∗ ( s , a ) q^*(s, a) q∗(s,a) 最大的对应 π ( a ∣ s ) \pi (a|s) π(a∣s) 为 1, 其它 为 0 。可获得 最大值。
正是证明了之前提到的 最优策略 π ( s ) π(s) π(s) 是选择具有 最大 q ( s , a ) q(s, a) q(s,a) 的动作的策略。
v ∗ v^* v∗ 的值是唯一的,但 v ∗ v^* v∗ 对应的最优策略可能不是唯一的。
————————
3.5 哪些因素影响最佳策略
P4 3.5
什么因素 决定最优策略 ?
最优策略的影响因素: 回报 r r r,折扣率 γ \gamma γ

γ \gamma~ γ 小, 短视;即时奖励 [选择即时奖励最大的行动,而不是总回报最大的行动。]
γ \gamma~ γ 大,目光长远; 延迟奖励
靠近目标的状态值较大,而远离目标的状态值较低。
- 如果一个状态必须沿着更长的轨迹到达目标,那么由于折扣率的存在,它的状态值就会变小。
r r~ r 只关心 动作间的 奖励相对值。
$r~$ 友好的 波浪线强制空格

- 证明 4: 对所有 reward 统一进行 仿射变换, 最优策略 保持不变 P62- [见 后文补充]
当奖励都为 正 或 都为负的时候 可以 依据 以上定理 进行变换。最优策略 只和 奖励间的 相对值 有关
例子:
绕路
贝尔曼最优方程的 解对应 最佳状态值 和 最优策略。
小结:

3.7 节
什么是最优策略?
如果一个策略对应的状态值大于或等于任何其他策略,则该策略是最优的。
应该注意的是,这个特定的最优性定义仅对表格强化学习算法有效。当值或策略由函数近似时,必须使用不同的度量来定义最优策略。
最优政策是随机的还是确定的 ?
最优策略可以是确定性的,也可以是随机的。一个很好的事实是,总是存在确定性贪婪最优策略。
如果我们希望最优策略在到达目标之前避免无意义的弯路,我们是否应该在每一步都增加一个负奖励,以使 agent 尽快到达目标?
首先,在每一步中引入一个额外的负奖励是奖励的仿射变换,它不会改变最优策略。其次,折扣率可以自动鼓励 agent 尽快达到目标。这是因为无意义的弯路会增加轨迹长度,减少 discounted return。
-——————
习题 笔记:
最优策略不一定唯一。
补充
证明 1: 压缩映射定理

压缩映射定理 不仅可以判断非线性方程的解是否存在,而且还提供了求解该方程的数值算法。 x k + 1 = f ( x k ) x_{k+1}=f(x_k) xk+1=f(xk)。不断迭代即可获得 解。
P8 Box 3.1
补充:


根据 柯西极限存在准则,证明 不动点 存在。
1、证明 当 { x k } k = 1 ∞ \{x_k\}_{k=1}^\infty {xk}k=1∞ 时, x k = f ( x k − 1 ) x_k=f(x_{k-1}) xk=f(xk−1) 收敛。
这个证明依赖于柯西序列。一个序列 x 1 , x 2 , ⋯ ∈ R x_1, x_2, \cdots \in \mathbb R x1,x2,⋯∈R, 如果对于任何小的 ε > 0 \varepsilon > 0 ε>0,存在 N N N, 对于所有 m , n > N m, n > N m,n>N, 使得 ∣ ∣ x m − x n ∣ ∣ < ε ||x_m - x_n|| < \varepsilon ∣∣xm−xn∣∣<ε。
直观的解释是存在一个有限整数 N N N, 使得 N N N 之后的所有元素彼此足够接近。
柯西序列之所以重要,是因为它保证了柯西序列收敛于某个有限值。
它的收敛性将用于证明 压缩映射定理。
注意,对于所有的 m , n > N m,n > N m,n>N,我们必须有 ∣ ∣ x m − x n ∣ ∣ < ε ||x_m - x_n|| < ε ∣∣xm−xn∣∣<ε。
如果我们仅仅有 x n + 1 − x n → 0 x_{n+1} - x_n→0 xn+1−xn→0,就不足以断言这个序列是柯西序列。
例如,对于 x n = n x_n= \sqrt n xn=n, x n + 1 − x n → 0 x_{n+1} - x_n→0 xn+1−xn→0 成立,但显然, x n = n x_n= \sqrt n xn=n 是发散的。
证明 { x k = f ( x k − 1 ) } k = 1 ∞ \{x_k=f(x_{k-1})\}_{k=1}^\infty {xk=f(xk−1)}k=1∞ 是柯西序列, 因此是 收敛的。
——————————————
由于 f f f 是 收缩映射, 则有
∣ ∣ x k + 1 − x k ∣ ∣ = ∣ ∣ f ( x k ) − f ( x k − 1 ) ∣ ∣ ≤ γ ∣ ∣ x k − x k − 1 ∣ ∣ ||x_{k+1}-x_k||=||f(x_k)-f(x_{k-1})||\leq\gamma||x_k-x_{k-1}|| ∣∣xk+1−xk∣∣=∣∣f(xk)−f(xk−1)∣∣≤γ∣∣xk−xk−1∣∣
类似地 ,有
∣ ∣ x k − x k − 1 ∣ ∣ ≤ γ ∣ ∣ x k − 1 − x k − 2 ∣ ∣ ||x_k-x_{k-1}||\leq\gamma||x_{k-1}-x_{k-2}|| ∣∣xk−xk−1∣∣≤γ∣∣xk−1−xk−2∣∣
⋮ \vdots ⋮
∣ ∣ x 2 − x 1 ∣ ∣ ≤ γ ∣ ∣ x 1 − x 0 ∣ ∣ ||x_2-x_1||\leq\gamma||x_1-x_0|| ∣∣x2−x1∣∣≤γ∣∣x1−x0∣∣
则
∣ ∣ x k + 1 − x k ∣ ∣ ≤ γ ∣ ∣ x k − x k − 1 ∣ ∣ ≤ γ 2 ∣ ∣ x k − 1 − x k − 2 ∣ ∣ ⋮ ≤ γ k ∣ ∣ x 1 − x 0 ∣ ∣ \begin{aligned}||x_{k+1}-x_k||&\leq\gamma||x_k-x_{k-1}||\\ &\leq\gamma^2||x_{k-1}-x_{k-2}||\\ & \vdots\\ &\leq\gamma^k||x_1-x_0||\end{aligned} ∣∣xk+1−xk∣∣≤γ∣∣xk−xk−1∣∣≤γ2∣∣xk−1−xk−2∣∣⋮≤γk∣∣x1−x0∣∣
由于 γ < 1 \gamma < 1 γ<1, 对 任意 x 1 , x 0 x_1, x_0 x1,x0 ,当 k → ∞ k\to \infty k→∞, ∣ ∣ x k + 1 − x k ∣ ∣ ||x_{k+1}-x_k|| ∣∣xk+1−xk∣∣ 以指数速度 收敛到 0。
正如 前文所述, 仅满足 x n + 1 − x n → 0 x_{n+1} - x_n→0 xn+1−xn→0 , 无法得到 收敛的结论。 如 发散 的 x n = n x_n= \sqrt n xn=n 。
需要进一步考虑 m > n m > n m>n 时,
∣ ∣ x m − x n ∣ ∣ = ∣ ∣ x m − x m − 1 + x m − 1 − ⋯ − x n + 1 + x n + 1 − x n ∣ ∣ ≤ ∣ ∣ x m − x m − 1 ∣ ∣ + ⋯ + ∣ ∣ x n + 1 − x n ∣ ∣ ≤ γ m − 1 ∣ ∣ x 1 − x 0 ∣ ∣ + ⋯ + γ n ∣ ∣ x 1 − x 0 ∣ ∣ = γ n ( γ m − 1 − n + ⋯ + 1 ) ∣ ∣ x 1 − x 0 ∣ ∣ ≤ γ n ⋅ ∑ i = 1 ∞ γ i ⋅ ∣ ∣ x 1 − x 0 ∣ ∣ γ 的幂次项扩展到无穷多项 = γ n 1 − γ ∣ ∣ x 1 − x 0 ∣ ∣ \begin{aligned}||x_m-x_n||&=||x_m-x_{m-1}+x_{m-1}-\cdots-x_{n+1}+x_{n+1}-x_n||\\ &\leq ||x_m-x_{m-1}||+\cdots+||x_{n+1}-x_n||\\ &\leq \gamma^{m-1} ||x_1-x_0||+\cdots+\gamma^n||x_1-x_0||\\ &=\gamma^n(\gamma^{m-1-n}+\cdots+1)||x_1-x_0||\\ &\leq\gamma^n·\sum\limits_{i=1}^\infty\gamma^i·||x_1-x_0||~~~~~~~\textcolor{blue}{\gamma ~的幂次项扩展到无穷多项}\\ &=\frac{\gamma^n}{1-\gamma} ||x_1-x_0||\\ \end{aligned} ∣∣xm−xn∣∣=∣∣xm−xm−1+xm−1−⋯−xn+1+xn+1−xn∣∣≤∣∣xm−xm−1∣∣+⋯+∣∣xn+1−xn∣∣≤γm−1∣∣x1−x0∣∣+⋯+γn∣∣x1−x0∣∣=γn(γm−1−n+⋯+1)∣∣x1−x0∣∣≤γn⋅i=1∑∞γi⋅∣∣x1−x0∣∣ γ 的幂次项扩展到无穷多项=1−γγn∣∣x1−x0∣∣
对于右侧, γ < 1 \gamma<1 γ<1,为某个 小的值
对任意小的 ε \varepsilon ε, 总能找到 N N N, 使得当 m , n > N m, n > N m,n>N ,有 ∣ ∣ x m − x n ∣ ∣ < ε ||x_m - x_n|| < ε ∣∣xm−xn∣∣<ε,满足柯西极限存在准则, 数列 { x k } \{x_k\} {xk} 收敛。
假设收敛到 x ∗ x^* x∗, lim k → ∞ x k = x ∗ \lim\limits_{k\to\infty}x_k=x^* k→∞limxk=x∗。
2、证明 x ∗ = lim k → ∞ x k x^*=\lim\limits_{k\to\infty}x_k x∗=k→∞limxk 是一个不动点。
由于 ∣ ∣ f ( x k ) − x k ∣ ∣ = ∣ ∣ x k + 1 − x k ∣ ∣ ≤ γ k ∣ ∣ x 1 − x 0 ∣ ∣ ||f(x_k)-x_k||=||x_{k+1}-x_k||\leq\gamma^k||x_1-x_0|| ∣∣f(xk)−xk∣∣=∣∣xk+1−xk∣∣≤γk∣∣x1−x0∣∣
已知 ∣ ∣ f ( x k ) − x k ∣ ∣ ||f(x_k)-x_k|| ∣∣f(xk)−xk∣∣ 以指数速度 收敛于 0。则 f ( x ∗ ) = x ∗ f(x^*)=x^*~~~ f(x∗)=x∗ 两边同时 取极限
lim k → ∞ ∣ ∣ f ( x k ) − x k ∣ ∣ = 0 \lim\limits_{k\to\infty}||f(x_k)-x_k||=0 k→∞lim∣∣f(xk)−xk∣∣=0
3、证明 不动点 唯一。
假设 存在另外的不动点 x ′ x^\prime x′, 满足 f ( x ′ ) = x ′ f(x^\prime) =x^\prime f(x′)=x′
∣ ∣ x ′ − x ∗ ∣ ∣ = ∣ ∣ f ( x ′ ) − f ( x ∗ ) ∣ ∣ ≤ γ ∣ ∣ x ′ − x ∗ ∣ ∣ ||x^\prime-x^*||=||f(x^\prime)-f(x^*)||\leq\gamma||x^\prime-x^*|| ∣∣x′−x∗∣∣=∣∣f(x′)−f(x∗)∣∣≤γ∣∣x′−x∗∣∣
由于 γ < 1 \gamma < 1 γ<1, 当且仅当 ∣ ∣ x ′ − x ∗ ∣ ∣ = 0 ||x^\prime-x^*||=0 ∣∣x′−x∗∣∣=0 时不等式成立。因此, 只能是 x ′ = x ∗ x^\prime=x^* x′=x∗。
或者不等式两边同除 ∣ ∣ x ′ − x ∗ ∣ ∣ ||x^\prime-x^*|| ∣∣x′−x∗∣∣, 得到 γ ≥ 1 \gamma\geq1 γ≥1,与题设 γ < 1 \gamma < 1 γ<1矛盾,因此不动点唯一。
4、证明 x k x_k xk 以指数速度收敛于 x ∗ x^* x∗。
由之前的 ∣ ∣ x m − x n ∣ ∣ ≤ γ n 1 − γ ∣ ∣ x 1 − x 0 ∣ ∣ ||x_m-x_n|| \leq \frac{\gamma^n}{1-\gamma}||x_1-x_0|| ∣∣xm−xn∣∣≤1−γγn∣∣x1−x0∣∣
由于 m m m 可以是任意大。
x ∗ − x n = lim m → ∞ ∣ ∣ x m − x n ∣ ∣ ≤ γ n 1 − γ ∣ ∣ x 1 − x 0 ∣ ∣ x^*-x_n =\lim\limits_{m\to\infty}||x_m-x_n||\leq \frac{\gamma^n}{1-\gamma}||x_1-x_0|| x∗−xn=m→∞lim∣∣xm−xn∣∣≤1−γγn∣∣x1−x0∣∣
由于 γ < 1 \gamma<1 γ<1, 当 n → ∞ n→∞ n→∞ 时,误差以指数速度 收敛于 0。
——————————
补充: 参考链接




其它可参考链接:
链接 1:数分之梯丨压缩映射定理——同济大学陈滨
链接 2:柯西收敛准则有啥用?当然是证明压缩映射原理!
证明 2:证明 贝尔曼最优方程 的右侧 是 压缩映射的


考虑 两个 向量 v 1 , v 2 ∈ R ∣ S ∣ \bm v_1, \bm v_2\in \mathbb R^{|\cal S|} v1,v2∈R∣S∣
π 1 ∗ = ˙ arg max π ( r π + γ P π v 1 ) \pi_1^*\dot=\arg\max\limits_\pi(\bm r_\pi+\gamma\bm P_\pi\bm v_1) π1∗=˙argπmax(rπ+γPπv1)
π 2 ∗ = ˙ arg max π ( r π + γ P π v 2 ) \pi_2^*\dot=\arg\max\limits_\pi(\bm r_\pi+\gamma\bm P_\pi\bm v_2) π2∗=˙argπmax(rπ+γPπv2)
f ( v 1 ) = max π ( r π + γ P π v 1 ) = r π 1 ∗ + γ P π 1 ∗ v 1 ≥ r π 2 ∗ + γ P π 2 ∗ v 1 f(\bm v_1)=\max\limits_\pi(\bm r_\pi+\gamma\bm P_\pi\bm v_1)=\bm r_{\pi_1^*}+\gamma\bm P_{\pi_1^*}\bm v_1\geq \bm r_{\pi_2^*}+\gamma\bm P_{\pi_2^*}\bm v_1~~~~~ f(v1)=πmax(rπ+γPπv1)=rπ1∗+γPπ1∗v1≥rπ2∗+γPπ2∗v1 对于同一状态值 v 1 v_1 v1 ,最佳策略 π 1 ∗ \pi_1^* π1∗ 相应的状态值 必然大于 其它策略的
f ( v 2 ) = max π ( r π + γ P π v 2 ) = r π 2 ∗ + γ P π 2 ∗ v 2 ≥ r π 1 ∗ + γ P π 1 ∗ v 2 f(\bm v_2)=\max\limits_\pi(\bm r_\pi+\gamma\bm P_\pi\bm v_2)=\bm r_{\pi_2^*}+\gamma\bm P_{\pi_2^*}\bm v_2\geq \bm r_{\pi_1^*}+\gamma\bm P_{\pi_1^*}\bm v_2~~~~~ f(v2)=πmax(rπ+γPπv2)=rπ2∗+γPπ2∗v2≥rπ1∗+γPπ1∗v2
≥ \geq ≥ 是 元素级的。
f ( v 1 ) − f ( v 2 ) = r π 1 ∗ + γ P π 1 ∗ v 1 − ( r π 2 ∗ + γ P π 2 ∗ v 2 ) ≤ r π 1 ∗ + γ P π 1 ∗ v 1 − ( r π 1 ∗ + γ P π 1 ∗ v 2 ) = γ P π 1 ∗ ( v 1 − v 2 ) \begin{aligned}f(\bm v_1)-f(\bm v_2)&=\bm r_{\pi_1^*}+\gamma\bm P_{\pi_1^*}\bm v_1-(\bm r_{\pi_2^*}+\gamma\bm P_{\pi_2^*}\bm v_2)\\ &\leq \bm r_{\pi_1^*}+\gamma\bm P_{\pi_1^*}\bm v_1-(\bm r_{\pi_1^*}+\gamma\bm P_{\pi_1^*}\bm v_2)\\ &=\gamma\bm P_{\pi_1^*}(\bm v_1-\bm v_2)\end{aligned} f(v1)−f(v2)=rπ1∗+γPπ1∗v1−(rπ2∗+γPπ2∗v2)≤rπ1∗+γPπ1∗v1−(rπ1∗+γPπ1∗v2)=γPπ1∗(v1−v2)
f ( v 2 ) − f ( v 1 ) = r π 2 ∗ + γ P π 2 ∗ v 2 − ( r π 1 ∗ + γ P π 1 ∗ v 1 ) ≤ r π 2 ∗ + γ P π 2 ∗ v 2 − ( r π 2 ∗ + γ P π 2 ∗ v 1 ) = γ P π 2 ∗ ( v 2 − v 1 ) \begin{aligned}f(\bm v_2)-f(\bm v_1)&=\bm r_{\pi_2^*}+\gamma\bm P_{\pi_2^*}\bm v_2-(\bm r_{\pi_1^*}+\gamma\bm P_{\pi_1^*}\bm v_1)\\ &\leq \bm r_{\pi_2^*}+\gamma\bm P_{\pi_2^*}\bm v_2-(\bm r_{\pi_2^*}+\gamma\bm P_{\pi_2^*}\bm v_1)\\ &=\gamma\bm P_{\pi_2^*}(\bm v_2-\bm v_1)\end{aligned} f(v2)−f(v1)=rπ2∗+γPπ2∗v2−(rπ1∗+γPπ1∗v1)≤rπ2∗+γPπ2∗v2−(rπ2∗+γPπ2∗v1)=γPπ2∗(v2−v1)
γ P π 2 ∗ ( v 1 − v 2 ) ≤ f ( v 1 ) − f ( v 2 ) ≤ γ P π 1 ∗ ( v 1 − v 2 ) \gamma\bm P_{\pi_2^*}(\bm v_1-\bm v_2)\leq f(\bm v_1)-f(\bm v_2)\leq \gamma\bm P_{\pi_1^*}(\bm v_1-\bm v_2) γPπ2∗(v1−v2)≤f(v1)−f(v2)≤γPπ1∗(v1−v2)
令 z = ˙ max { ∣ γ P π 2 ∗ ( v 1 − v 2 ) ∣ , ∣ γ P π 1 ∗ ( v 1 − v 2 ) ∣ } ∈ R ∣ S ∣ z\dot=\max~\{|\gamma\bm P_{\pi_2^*}(\bm v_1-\bm v_2)|, |\gamma\bm P_{\pi_1^*}(\bm v_1-\bm v_2)|\}\in\mathbb R^{|\cal S|} z=˙max {∣γPπ2∗(v1−v2)∣,∣γPπ1∗(v1−v2)∣}∈R∣S∣
z ≥ 0 z\geq0 z≥0
− z ≤ γ P π 2 ∗ ( v 1 − v 2 ) ≤ f ( v 1 ) − f ( v 2 ) ≤ γ P π 1 ∗ ( v 1 − v 2 ) ≤ z -z\leq\gamma\bm P_{\pi_2^*}(\bm v_1-\bm v_2)\leq f(\bm v_1)-f(\bm v_2)\leq \gamma\bm P_{\pi_1^*}(\bm v_1-\bm v_2)\leq z −z≤γPπ2∗(v1−v2)≤f(v1)−f(v2)≤γPπ1∗(v1−v2)≤z
∣ f ( v 1 ) − f ( v 2 ) ∣ ≤ z |f(\bm v_1)-f(\bm v_2)|\leq z ∣f(v1)−f(v2)∣≤z
最大模 ∣ ∣ f ( v 1 ) − f ( v 2 ) ∣ ∣ ∞ ≤ ∣ ∣ z ∣ ∣ ∞ ||f(\bm v_1)-f(\bm v_2)||_\infty\leq ||z||_\infty ∣∣f(v1)−f(v2)∣∣∞≤∣∣z∣∣∞
p i T p_i^T piT, q i T q_i^T qiT 分别为 P π 1 ∗ \bm P_{\pi_1^*} Pπ1∗ 和 P π 2 ∗ \bm P_{\pi_2^*} Pπ2∗ 的 第 i i i 行。
z i = max { γ ∣ p i T ( v 1 − v 2 ) ∣ , γ ∣ q i T ( v 1 − v 2 ) ∣ } z_i=\max~\{\gamma |p_i^T(\bm v_1-\bm v_2)|, \gamma|q_i^T(\bm v_1-\bm v_2)|\} zi=max {γ∣piT(v1−v2)∣,γ∣qiT(v1−v2)∣}
p i p_i pi 是一个包含所有非负元素的向量并且所有元素的和等于 1。
∣ p i T ( v 1 − v 2 ) ∣ ≤ p i T ∣ v 1 − v 2 ∣ ≤ ∣ ∣ v 1 − v 2 ∣ ∣ ∞ |p_i^T(\bm v_1-\bm v_2)|\leq p_i^T|\bm v_1-\bm v_2|\leq||\bm v_1-\bm v_2||_\infty ∣piT(v1−v2)∣≤piT∣v1−v2∣≤∣∣v1−v2∣∣∞
类似地 , ∣ q i T ( v 1 − v 2 ) ∣ ≤ ∣ ∣ v 1 − v 2 ∣ ∣ ∞ |q_i^T(\bm v_1-\bm v_2)|\leq||\bm v_1-\bm v_2||_\infty ∣qiT(v1−v2)∣≤∣∣v1−v2∣∣∞
z i ≤ γ ∣ ∣ v 1 − v 2 ∣ ∣ ∞ z_i\leq\gamma||\bm v_1-\bm v_2||_\infty zi≤γ∣∣v1−v2∣∣∞
∣ ∣ z ∣ ∣ ∞ = max i ∣ z i ∣ ≤ γ ∣ ∣ v 1 − v 2 ∣ ∣ ∞ ||z||_\infty=\max\limits_i|z_i|\leq\gamma||\bm v_1-\bm v_2||_\infty ∣∣z∣∣∞=imax∣zi∣≤γ∣∣v1−v2∣∣∞
即 ∣ ∣ f ( v 1 ) − f ( v 2 ) ∣ ∣ ∞ ≤ γ ∣ ∣ v 1 − v 2 ∣ ∣ ∞ ||f(\bm v_1)-f(\bm v_2)||_\infty\leq \gamma||\bm v_1-\bm v_2||_\infty ∣∣f(v1)−f(v2)∣∣∞≤γ∣∣v1−v2∣∣∞
证毕。
证明 3: 贝尔曼最优方程的解对应 最大状态值 和 最优策略

P58
对于 任意 策略 π \pi π, 满足 贝尔曼方程为 v π = r π + γ P π v π v_\pi=r_\pi+\gamma P_\pi v_\pi vπ=rπ+γPπvπ
由于 最优策略 v ∗ = max π ( r π + γ P π v ∗ ) = r π ∗ + γ P π ∗ v ∗ ≥ r π + γ P π v ∗ v^*=\max\limits_\pi(r_\pi+\gamma P_\pi v^*)=r_{\pi^*}+\gamma P_{\pi^*} v^*\geq r_\pi+\gamma P_\pi v^* v∗=πmax(rπ+γPπv∗)=rπ∗+γPπ∗v∗≥rπ+γPπv∗
v ∗ − v π ≥ r π ∗ + γ P π ∗ v ∗ − ( r π + γ P π v π ) = γ P π ( v ∗ − v π ) v^*-v_\pi\geq r_{\pi^*}+\gamma P_{\pi^*} v^*-(r_\pi+\gamma P_\pi v_\pi)=\gamma P_\pi (v^*-v_\pi) v∗−vπ≥rπ∗+γPπ∗v∗−(rπ+γPπvπ)=γPπ(v∗−vπ)
重复应用上述不等式:
v ∗ − v π ≥ γ P π ( v ∗ − v π ) ≥ γ 2 P π 2 ( v ∗ − v π ) ≥ ⋯ ≥ γ n P π n ( v ∗ − v π ) v^*-v_\pi\geq\gamma P_\pi (v^*-v_\pi)\geq\gamma^2 P^2_\pi (v^*-v_\pi)\geq\cdots\geq\gamma^n P^n_\pi (v^*-v_\pi) v∗−vπ≥γPπ(v∗−vπ)≥γ2Pπ2(v∗−vπ)≥⋯≥γnPπn(v∗−vπ)
v ∗ − v π ≤ lim n → ∞ γ n P π n ( v ∗ − v π ) = 0 v^*-v_\pi\leq\lim\limits_{n\to\infty}\gamma^n P^n_\pi (v^*-v_\pi)=0 v∗−vπ≤n→∞limγnPπn(v∗−vπ)=0
由于 γ < 1 \gamma<1 γ<1 且 P π n P^n_\pi Pπn 是 元素均小于或等于 1 的非负矩阵 P π n 1 = 1 P^n_\pi \bm1=\bm1 Pπn1=1
因此 v ∗ ≥ v π v^*\geq v_\pi v∗≥vπ 对于任意 π \pi π 均成立。
证明 4: 对所有 reward 统一进行 仿射变换, 最优策略 不变

最优策略不变性
最优策略 v ∗ = max π ( r π + γ P π v ∗ ) \bm v^*=\max\limits_\pi(\bm r_\pi+\gamma \bm P_\pi \bm v^*) v∗=πmax(rπ+γPπv∗)
对 其中的 每个奖励值 r r r 都进行 仿射变换 α r + β \alpha r + \beta αr+β
则相应的 最优 状态值 v ′ = α v ∗ + β 1 − γ [ 1 1 . . . 1 1 ] \bm v^\prime=\alpha \bm v^*+\frac{\beta}{1-\gamma}\begin{bmatrix}1\\1\\...\\1\\1\end{bmatrix} v′=αv∗+1−γβ 11...11
其中 折扣率 γ ∈ ( 0 , 1 ) \gamma \in (0, 1) γ∈(0,1)
由 v ′ \bm v^\prime v′ 得到的最优策略 对于奖励值的仿射变换是不变的。
————————————————————————
P62 -
证明:
对 任意 策略 π \pi π, 令 r π = [ ⋯ , r π ( s ) , ⋯ ] T r_\pi=[\cdots,r_\pi(s), \cdots]^T rπ=[⋯,rπ(s),⋯]T
r π ( s ) = ∑ a ∈ A π ( a ∣ s ) ∑ r ∈ R p ( r ∣ s , a ) r , s ∈ S r_\pi(s)= \sum\limits_{a\in\cal A}\pi(a|s)\sum\limits_{r\in\cal R}p(r|s, a)r,~~~~~s\in\cal S rπ(s)=a∈A∑π(a∣s)r∈R∑p(r∣s,a)r, s∈S
如果 r → α r + β r\to\alpha r+\beta r→αr+β, 则 r π ( s ) → α r π ( s ) + β r_\pi(s)\to\alpha r_\pi(s)+\beta rπ(s)→αrπ(s)+β
r π → α r π + β 1 r_\pi\to\alpha r_\pi+\beta{\bf1} rπ→αrπ+β1, 其中 1 = [ 1 , ⋯ , 1 ] T \bm 1=[1, \cdots,1]^T 1=[1,⋯,1]T
此时, 贝尔曼最优公式 变成:
v ′ = max π ( α r π + β 1 + γ P π v ′ ) ( 3.9 ) \bm v^\prime=\max\limits_\pi(\alpha\bm r_\pi+\beta \bm1+\gamma\bm P_\pi\bm v^\prime)~~~~~~~~~~~~~~(3.9) v′=πmax(αrπ+β1+γPπv′) (3.9)
设 v ′ = α v ∗ + c 1 \bm v^\prime=\alpha \bm v^*+c\bm 1 v′=αv∗+c1 是 上述 式 (3.9) 的解
将 v ′ = α v ∗ + c 1 \bm v^\prime=\alpha \bm v^*+c\bm 1 v′=αv∗+c1 代入 (3.9)
α v ∗ + c 1 = max π ( α r π + β 1 + γ P π ( α v ∗ + c 1 ) ) = max π ( α r π + β 1 + γ α P π v ∗ + γ c 1 ) \alpha \bm v^*+c\bm 1=\max\limits_\pi\Big(\alpha\bm r_\pi+\beta \bm1+\gamma\bm P_\pi(\alpha \bm v^*+c\bm 1)\Big)=\max\limits_\pi (\alpha\bm r_\pi+\beta \bm1+\gamma\alpha\bm P_\pi \bm v^*+\gamma c\bm 1 ) αv∗+c1=πmax(αrπ+β1+γPπ(αv∗+c1))=πmax(αrπ+β1+γαPπv∗+γc1)
注意 P π 1 = 1 \bm P_\pi\bm 1=\bm1 Pπ1=1
α v ∗ = max π ( α r π + γ α P π v ∗ ) ⏟ α v ∗ + β 1 + + γ c 1 − c 1 \alpha\bm v^*=\underbrace{\max\limits_\pi (\alpha\bm r_\pi+ \gamma\alpha\bm P_\pi \bm v^*)}_{\alpha\bm v^*}+\beta \bm1++\gamma c\bm 1-c\bm1 αv∗=αv∗ πmax(αrπ+γαPπv∗)+β1++γc1−c1
即 β 1 + + γ c 1 − c 1 = 0 \beta \bm1++\gamma c\bm 1-c\bm1=0 β1++γc1−c1=0
c = β 1 − γ c=\frac{\beta}{1-\gamma} c=1−γβ
说明 v ′ = α v ∗ + c 1 \bm v^\prime=\alpha \bm v^*+c\bm 1 v′=αv∗+c1 是 式 (3.9) 的解,其中 c = β 1 − γ c=\frac{\beta}{1-\gamma} c=1−γβ。
又因为 式 (3.9) 也是 贝尔曼最优公式, v ′ v^\prime v′ 就是唯一解。
由于 v ′ v^\prime v′ 是 v ∗ v^* v∗ 的 仿射变换,状态值 之间的 相对关系 保持不变。
因此, 根据 v ′ v^\prime v′ 得到的贪心最优策略 和 v ∗ v^* v∗ 的一样。
相关文章:

⭐ ▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch3 贝尔曼最优公式 【压缩映射定理】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍 1、视频 学堂在线 习题 2、过 电子书,补充 【下载:本章 PDF 电子书 GitHub 界面链接】 [又看了一遍视频] 3、总体 MOOC 过一遍 习题 学堂在线 课程页面链接 中国大学MOOC 课程页面链接 B 站 视频链…...

Pikachu上的CSRF以及NSSCTF上的[NISACTF 2022]bingdundun~、 [SWPUCTF 2022 新生赛]xff
目录 一、CSRF CSRF(get) login CSRF(post) CSRF Token 二、CSRF的相关知识点 (1)什么是CSRF? (2)工作原理 (3)CSRF漏洞形成的条件 1、用户要在登录状态(即浏览器保存了该…...

大数据分析-二手车用户数据可视化分析
项目背景 在当今的大数据时代,数据可视化扮演着至关重要的角色。随着信息的爆炸式增长,我们面临着前所未有的数据挑战。这些数据可能来自社交媒体、商业交易、科学研究、医疗记录等各个领域,它们庞大而复杂,难以通过传统的数据处…...
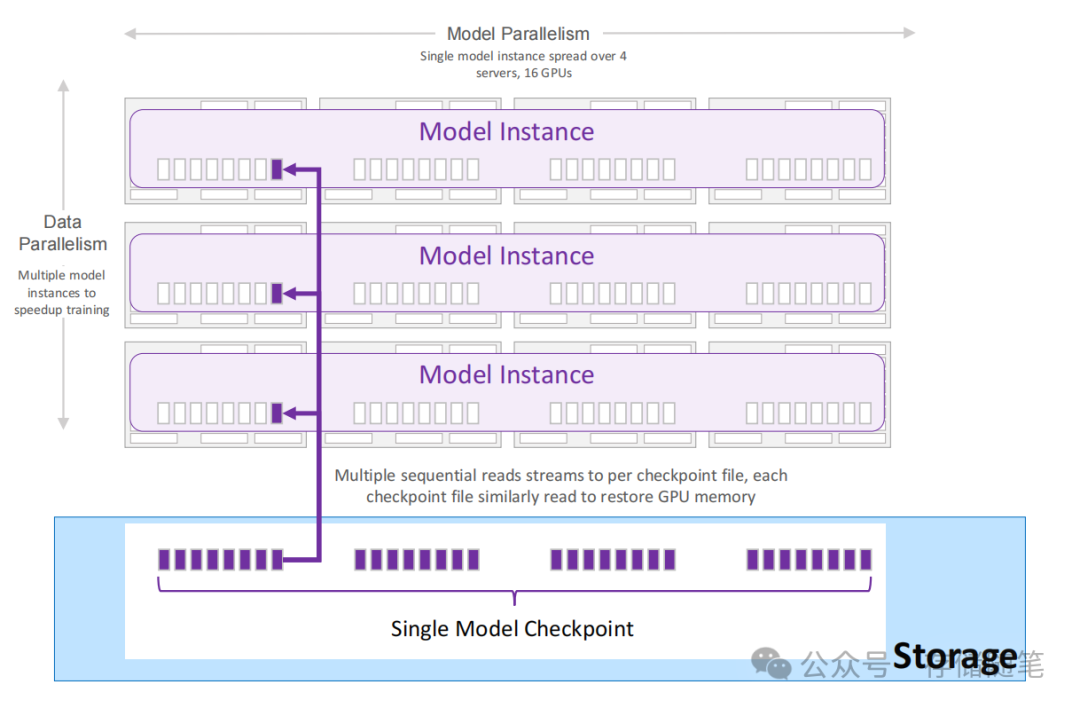
AI训练Checkpoint对存储的影响
检查点(Checkpoints)是机器学习和深度学习训练过程中的一个重要机制,旨在定期保存训练状态,以便在训练过程中遇到失败或中断时能够从中断处恢复训练,而无需从头开始。 随着模型参数量的剧增,Checkpoint文件…...

Python笔记 - 正则表达式
正则表达式(Regular Expression,简称regex)是一种强大的工具,用于匹配字符串模式。在Python中,正则表达式通过re模块提供。本文将带你深入了解Python中的正则表达式,从基础概念到高级用法。 1. 什么是正则…...

安卓网络通信(多线程、HTTP访问、图片加载、即时通信)
本章介绍App开发常用的以下网络通信技术,主要包括:如何以官方推荐的方式使用多线程技术,如何通过okhttp实现常见的HTTP接口访问操作,如何使用Dlide框架加载网络图片,如何分别运用SocketIO和WebSocket实现及时通信功能等…...

Virtual Memory Primitives for User Program翻译
Virtual Memory Primitives for User Program 安德鲁阿普尔(Andrew Appel)和李凯(Kai Li) 普林斯顿大学计算机科学系 摘要 传统上,内存管理单元(MMUS)被操作系统用于实现磁盘分页的虚拟内存…...
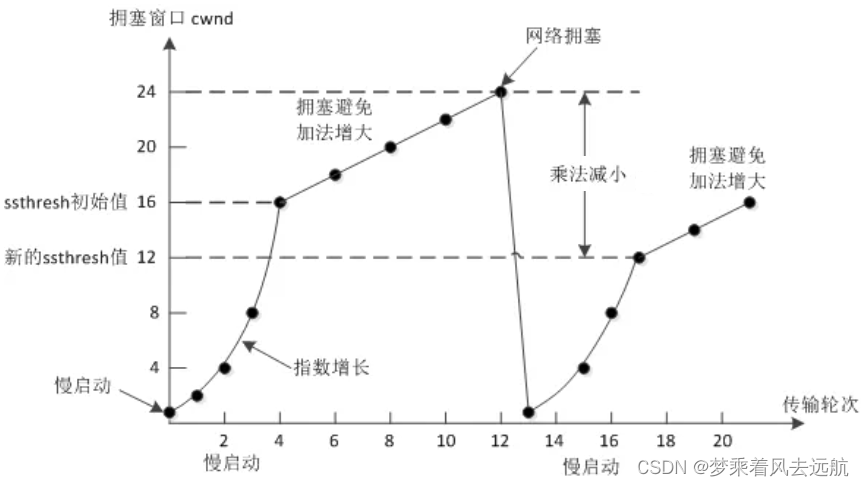
网络基础2
目录 应用层HTTP协议认识URLurlencode和urldecode HTTP协议格式http请求格式http响应格式 HTTP的方法GET与POST的区别 HTTP的状态码HTTP常见HeaderCookie与Session 传输层在谈端口号端口号范围划分认识知名端口号netstatpidof UDP协议UDP协议端格式UDP的特点面向数据报UDP的缓冲…...

C# 下载文件2
从服务下载压缩包 过程 发起请求 HttpWebRequest 断点续传 HttpWebRequest.AddRange() 获取服务资源的响应 HttpWebResponse 设置下载进度条 解压压缩包 ZipFile using System; using System.IO; using System.IO.Compression; using System.Net;namespace Test01 {clas…...

Unity | Tilemap系统
目录 一、准备工作 1.插件导入 2.资源导入 二、相关组件介绍 1.Grid组件 2.Tilemap组件 3.Tile 4.Tile Palette 5.Brushes 三、动态创建地图 四、其他功能 1.移动网格上物体 2.拖拽缩放地图 Unity Tilemap系统为2D游戏开发提供了一个直观且功能强大的平台ÿ…...

CSS选择符和可继承属性
属性选择符: 示例:a[target"_blank"] { text-decoration: none; }(选择所有target"_blank"的<a>元素) /* 选择所有具有class属性的h1元素 */ h1[class] { color: silver; } /* 选择所有具有hre…...

C++升级软件时删除老版本软件的桌面快捷方式(附源码)
删除桌面快捷方式其实是删除桌面上的快捷方式文件,那我们如何去删除桌面快捷方式文件呢?软件可能已经发布过多个版本,其中的一些版本的快捷方式文件名称可能做了多次改动,程序中不可能记录每个版本的快捷方式名称,没法直接去删除快捷方式文件。本文就给出一种有效的处理办…...
github国内加速访问有效方法
这里只介绍实测最有效的一种方法,修改主机的Hosts文件,如果访问github网站慢或者根本无法访问的时候可以采用下面方法进行解决。 1、搜索一个IP查询网站 首先百度搜索选择一个IP查询的网站,这里我用下面这个网站(如果该网站失效…...

如何处理JavaScript中的浮点数精度问题
在开发过程中,特别是涉及到金额计算或需要精确比较的场景,浮点数精度问题是一个常见而重要的挑战。本文将介绍在JavaScript中如何识别、理解和解决这些问题,并提供一些实用的技巧和建议。 1. 问题背景 JavaScript中的浮点数采用IEEE 754标准…...

ASPICE标准与ASPICE认证:提升汽车软件开发质量与效率的关键途径
在当今日新月异的科技时代,软件产品的质量和可靠性成为了企业赢得市场的关键。而ASPICE(Automotive SPICE)标准,作为汽车行业中软件过程评估的国际通用标准,正逐渐引起行业的广泛关注。那么,ASPICE标准究竟…...
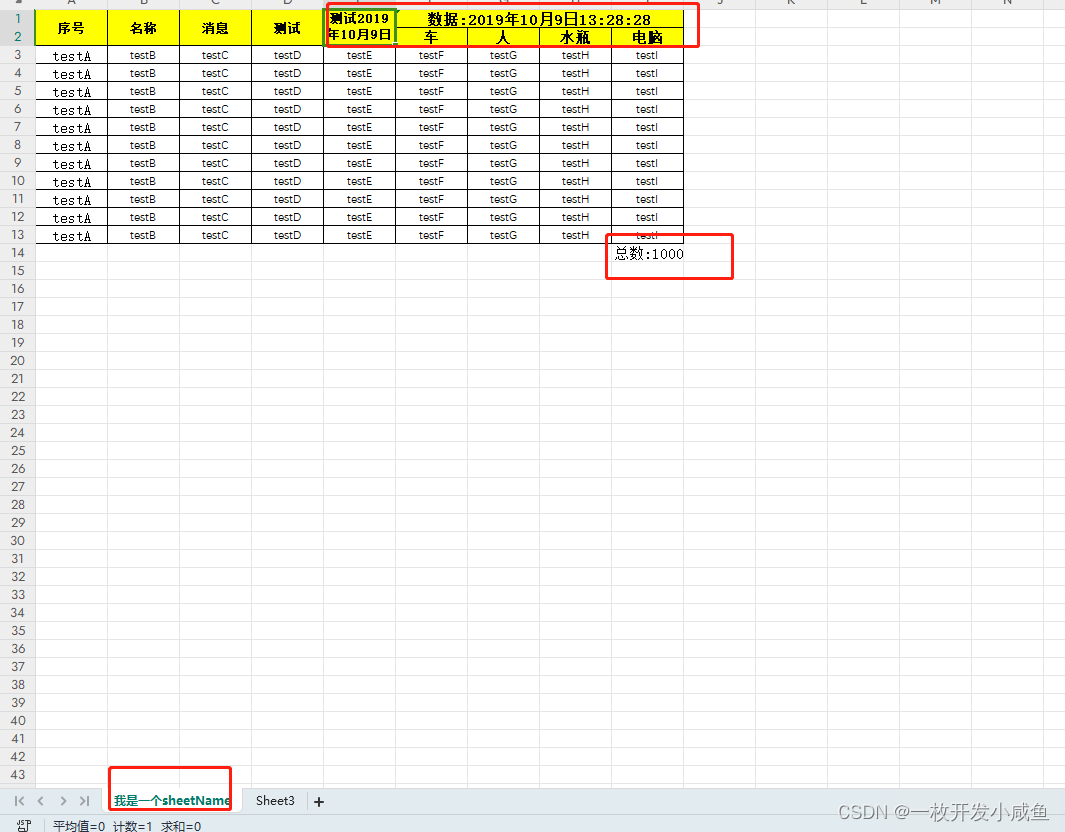
easyexcel的简单使用(execl模板导出)
模板支持功能点 支持列表支持自定义头名称支持自定义fileName支持汇总 模板示例 操作 pom引入 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>${easyexcel.version}</version></dep…...

代码随想录算法训练营第39天|● 62.不同路径 ●63. 不同路径 II
不同路径 62. 不同路径 - 力扣(LeetCode) 1.确定dp数组(dp table)以及下标的含义 dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。 2.确定递推公式 …...

【DevOps】 什么是容器 - 一种全新的软件部署方式
目录 引言 一、什么是容器 二、容器的工作原理 三、容器的主要特性 四、容器技术带来的变革 五、容器技术的主要应用场景 六、容器技术的主要挑战 七、容器技术的发展趋势 引言 在过去的几十年里,软件行业经历了飞速的发展。从最初的大型机时代,到后来的个人电脑时代,…...
使用pnpm创建vue3项目
https://pnpm.io/zh/ 全局安装: npm install -g pnpm 检查版本: pnpm -v 创建vue3项目: pnpm create vuelatest 项目装包: pnpm install 运行项目: pnpm dev 命令行: https://pnpm.io/zh/pnpm-cli pnpm …...

【软件测试】43个功能测试点总结
🍅 视频学习:文末有免费的配套视频可观看 🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 功能测试就是对产品的各功能进行验证,根据功能测试用例,逐项测试…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
