Part 4.2 背包动态规划
->背包模型模板(0/1,分组,完全,多重)<-
[NOIP2018 提高组] 货币系统
题目背景
NOIP2018 提高组 D1T2
题目描述
在网友的国度中共有 n n n 种不同面额的货币,第 i i i 种货币的面额为 a [ i ] a[i] a[i],你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 n n n、面额数组为 a [ 1.. n ] a[1..n] a[1..n] 的货币系统记作 ( n , a ) (n,a) (n,a)。
在一个完善的货币系统中,每一个非负整数的金额 x x x 都应该可以被表示出,即对每一个非负整数 x x x,都存在 n n n 个非负整数 t [ i ] t[i] t[i] 满足 a [ i ] × t [ i ] a[i] \times t[i] a[i]×t[i] 的和为 x x x。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 x x x 不能被该货币系统表示出。例如在货币系统 n = 3 n=3 n=3, a = [ 2 , 5 , 9 ] a=[2,5,9] a=[2,5,9] 中,金额 1 , 3 1,3 1,3 就无法被表示出来。
两个货币系统 ( n , a ) (n,a) (n,a) 和 ( m , b ) (m,b) (m,b) 是等价的,当且仅当对于任意非负整数 x x x,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 ( m , b ) (m,b) (m,b),满足 ( m , b ) (m,b) (m,b) 与原来的货币系统 ( n , a ) (n,a) (n,a) 等价,且 m m m 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 m m m。
输入格式
输入文件的第一行包含一个整数 T T T,表示数据的组数。
接下来按照如下格式分别给出 T T T 组数据。 每组数据的第一行包含一个正整数 n n n。接下来一行包含 n n n 个由空格隔开的正整数 a [ i ] a[i] a[i]。
输出格式
输出文件共有 T T T 行,对于每组数据,输出一行一个正整数,表示所有与 ( n , a ) (n,a) (n,a) 等价的货币系统 ( m , b ) (m,b) (m,b) 中,最小的 m m m。
样例 #1
样例输入 #1
2
4
3 19 10 6
5
11 29 13 19 17
样例输出 #1
2
5
提示
在第一组数据中,货币系统 ( 2 , [ 3 , 10 ] ) (2, [3,10]) (2,[3,10]) 和给出的货币系统 ( n , a ) (n, a) (n,a) 等价,并可以验证不存在 m < 2 m < 2 m<2 的等价的货币系统,因此答案为 2 2 2。 在第二组数据中,可以验证不存在 m < n m < n m<n 的等价的货币系统,因此答案为 5 5 5。
【数据范围与约定】

对于 100 % 100\% 100% 的数据,满足 1 ≤ T ≤ 20 , n , a [ i ] ≥ 1 1 ≤ T ≤ 20, n,a[i] ≥ 1 1≤T≤20,n,a[i]≥1。
解题思路
vis[i]=(vis[i-money[j]]>1)?2:0
vis[i]的值为0,说明不可得到值为i的数,1表示本来就存在值为i的面值,2表示可以拼凑得到值为i的面值,2可以覆盖1,从而达成减少种类的目的。
代码实现
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int t;
#define MAX_N 100
#define MAX_A 25000
int money[MAX_N+5];
int vis[MAX_A+5];
void solve()
{memset(vis,0,sizeof vis);int n;cin>>n;for(int i=1;i<=n;i++){cin>>money[i];vis[money[i]]=1;}sort(money+1,money+1+n);for(int i=1;i<=money[n];i++){for(int j=1;j<n;j++){if(money[j]>=i)break;if(!vis[i-money[j]])continue;vis[i]=2;}}int ans=0;for(int i=1;i<=money[n];i++)if(vis[i]==1)ans++;cout<<ans<<endl;
}
int main()
{cin>>t;while(t--)solve();return 0;
} 通天之分组背包
题目背景
直达通天路·小 A 历险记第二篇
题目描述
自 01 01 01 背包问世之后,小 A 对此深感兴趣。一天,小 A 去远游,却发现他的背包不同于 01 01 01 背包,他的物品大致可分为 k k k 组,每组中的物品相互冲突,现在,他想知道最大的利用价值是多少。
输入格式
两个数 m , n m,n m,n,表示一共有 n n n 件物品,总重量为 m m m。
接下来 n n n 行,每行 3 3 3 个数 a i , b i , c i a_i,b_i,c_i ai,bi,ci,表示物品的重量,利用价值,所属组数。
输出格式
一个数,最大的利用价值。
样例 #1
样例输入 #1
45 3
10 10 1
10 5 1
50 400 2
样例输出 #1
10
提示
0 ≤ m ≤ 1000 0 \leq m \leq 1000 0≤m≤1000, 1 ≤ n ≤ 1000 1 \leq n \leq 1000 1≤n≤1000, 1 ≤ k ≤ 100 1\leq k\leq 100 1≤k≤100, a i , b i , c i a_i, b_i, c_i ai,bi,ci 在 int 范围内。
解题思路
dp[i][j]:前i个分组在容量为觉得情况下的最大价值
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v]+w)
代码实现1
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX_N 1000
struct Data{int a,b,c;
}item[MAX_N+5];
int dp[MAX_N+5][MAX_N+5];//此处为前i个物品,容量为j的情况下的最大价值
bool cmp(Data a,Data b)
{return a.c<b.c;
}
int main()
{int m,n;cin>>m>>n;for(int i=1;i<=n;i++){cin>>item[i].a>>item[i].b>>item[i].c;}sort(item+1,item+n+1,cmp);int cnt=1;for(int i=1;i<=n;i++){if(item[i].c==item[i-1].c)cnt++;else cnt=1;for(int j=1;j<=m;j++){dp[i][j]=dp[i-1][j];if(j>=item[i].a)dp[i][j]=max(dp[i][j],dp[i-cnt][j-item[i].a]+item[i].b);}}cout<<dp[n][m];return 0;
}
代码实现2
#include<bits/stdc++.h>
using namespace std;
int v,n,t;
int x;
int g[205][205];
int i,j,k;
int w[10001],z[10001];
int b[10001];
int dp[10001];
int main(){cin>>v>>n;for(i=1;i<=n;i++){cin>>w[i]>>z[i]>>x;t=max(t,x);b[x]++;g[x][b[x]]=i;}for(i=1;i<=t;i++){for(j=v;j>=0;j--){for(k=1;k<=b[i];k++){if(j>=w[g[i][k]]){dp[j]=max(dp[j],dp[j-w[g[i][k]]]+z[g[i][k]]);}}}}cout<<dp[v];return 0;
}
[USACO09MAR] Cow Frisbee Team S
题目描述
老唐最近迷上了飞盘,约翰想和他一起玩,于是打算从他家的 N N N 头奶牛中选出一支队伍。
每只奶牛的能力为整数,第 i i i 头奶牛的能力为 R i R_i Ri。飞盘队的队员数量不能少于 1 1 1、大于 N N N。一支队伍的总能力就是所有队员能力的总和。
约翰比较迷信,他的幸运数字是 F F F,所以他要求队伍的总能力必须是 F F F 的倍数。请帮他算一下,符合这个要求的队伍组合有多少?由于这个数字很大,只要输出答案对 1 0 8 10^8 108 取模的值。
输入格式
第一行:两个用空格分开的整数: N N N 和 F F F。
第二行到 N + 1 N+1 N+1 行:第 i + 1 i+1 i+1 行有一个整数 R i R_i Ri,表示第 i i i 头奶牛的能力。
输出格式
第一行:单个整数,表示方案数对 1 0 8 10^8 108 取模的值。
样例 #1
样例输入 #1
4 5
1
2
8
2
样例输出 #1
3
提示
对于 100 % 100\% 100% 的数据, 1 ≤ N ≤ 2000 1 \le N \le 2000 1≤N≤2000, 1 ≤ F ≤ 1000 1 \le F \le 1000 1≤F≤1000, 1 ≤ R i ≤ 1 0 5 1 \le R_i \le 10^5 1≤Ri≤105。
解题思路
状态定义:dp[i][j]:前i头牛对f取模为j的方案总数
转移方程:dp[i][j]=dp[i-1][j]+dp[i-1][(j-val[i]%f+f)%f]
特别注意,对于每一个val[i]%f都要在dp[i][val[i]%f]的位置上加上一个1
代码实现
#include<iostream>
using namespace std;
#define MAX_N 2000
#define MAX_F 1000
#define MOD 100000000
int dp[2][MAX_F+5];
int val[MAX_N+5];
int n,f;
int main()
{cin>>n>>f;for(int i=1;i<=n;i++){cin>>val[i];val[i]%=f;}int now=0;for(int i=1;i<=n;i++){for(int j=0;j<f;j++){dp[now][j]=(dp[now^1][j]+dp[now^1][(j-val[i]+f)%f])%MOD;}dp[now][val[i]]+=1;now^=1;}cout<<dp[now^1][0];return 0;} 垃圾陷阱
题目描述
卡门――农夫约翰极其珍视的一条 Holsteins 奶牛――已经落了到 “垃圾井” 中。“垃圾井” 是农夫们扔垃圾的地方,它的深度为 D D D( 2 ≤ D ≤ 100 2 \le D \le 100 2≤D≤100)英尺。
卡门想把垃圾堆起来,等到堆得与井深同样高或比井深更高(即,垃圾高度总和 ≥ D \geq D ≥D)时,她就能逃出井外了。另外,卡门可以通过吃一些垃圾来维持自己的生命。
每个垃圾都可以用来吃或堆放,并且堆放垃圾不用花费卡门的时间。
假设卡门预先知道了每个垃圾扔下的时间 t t t( 1 ≤ t ≤ 1000 1 \le t \le 1000 1≤t≤1000),以及每个垃圾堆放的高度 h h h( 1 ≤ h ≤ 25 1 \le h \le 25 1≤h≤25)和吃进该垃圾能增加维持生命的时间 f f f( 1 ≤ f ≤ 30 1 \le f \le 30 1≤f≤30),要求出卡门最早能逃出井外的时间,假设卡门当前体内有足够持续 10 10 10 小时的能量,如果卡门 10 10 10 小时内(不含 10 10 10 小时,维持生命的时间同)没有进食,卡门就将饿死。特别地,若体力值为 0 0 0 时吃下垃圾或逃出井外也不会饿死。
输入格式
第一行为两个整数, D D D 和 G G G( 1 ≤ G ≤ 100 1 \le G \le 100 1≤G≤100), G G G 为被投入井的垃圾的数量。
第二到第 G + 1 G+1 G+1 行每行包括三个整数: T T T( 1 ≤ T ≤ 1000 1 \le T \le 1000 1≤T≤1000),表示垃圾被投进井中的时间; F F F( 1 ≤ F ≤ 30 1 \le F \le 30 1≤F≤30),表示该垃圾能维持卡门生命的时间;和 H H H( 1 ≤ H ≤ 25 1 \le H \le 25 1≤H≤25),该垃圾能垫高的高度。
输出格式
如果卡门可以爬出陷阱,输出一个整数,表示最早什么时候可以爬出;否则输出卡门最长可以存活多长时间。
样例 #1
样例输入 #1
20 4
5 4 9
9 3 2
12 6 10
13 1 1
样例输出 #1
13
提示
【样例说明】
卡门堆放她收到的第一个垃圾: h e i g h t = 9 \mathrm{height}=9 height=9;
卡门吃掉她收到的第 2 2 2 个垃圾,使她的生命从 10 10 10 小时延伸到 13 13 13 小时;
卡门堆放第 3 3 3 个垃圾, h e i g h t = 19 \mathrm{height}=19 height=19;
卡门堆放第 4 4 4 个垃圾, h e i g h t = 20 \mathrm{height}=20 height=20。
解题思路
状态定义:dp[i][j]表示前i个垃圾在能量为j的情况下的最大高度
转移方程:dp[i][j]=max(dp[i-1][j],dp[i-1][j-f]+h)
代码实现
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX_D 100
#define MAX_G 100
int d,g;
struct Data{int t,f,h;
}rubbish[MAX_G+5];
int dp[MAX_G+5][3010];
int vis[MAX_G+5][3010];
bool cmp(Data a,Data b)
{return a.t<b.t;
}
int main()
{cin>>d>>g;int max_t=0,sum_f=10;for(int i=1;i<=g;i++){cin>>rubbish[i].t>>rubbish[i].f>>rubbish[i].h;max_t=max(max_t,rubbish[i].t);sum_f+=rubbish[i].f;}sort(rubbish+1,rubbish+1+g,cmp);if(rubbish[1].t<=10){dp[1][10]=rubbish[1].h;if(rubbish[1].t!=10)vis[1][10]=1;vis[1][10+rubbish[1].f]=1;if(rubbish[1].h>=d){cout<<rubbish[1].t;return 0;}}for(int i=2;i<=g;i++){for(int j=10;j<=sum_f;j++){if(j<rubbish[i].t)continue;if((j-rubbish[i].f)>=rubbish[i].t&&vis[i-1][j-rubbish[i].f])//可以由dp[i-1][j-f]转移说明 j-f本身就要大于当前时间 dp[i][j]=dp[i-1][j-rubbish[i].f],vis[i][j]=1;if(vis[i-1][j])dp[i][j]=max(dp[i][j],dp[i-1][j]+rubbish[i].h),vis[i][j]=1;if(dp[i][j]>=d){cout<<rubbish[i].t;return 0;}}}int last=10;for(int i=1;i<=g;i++){if(last>=rubbish[i].t)last+=rubbish[i].f;else{cout<<last;return 0;}}cout<<last;return 0;} [BJOI2019] 排兵布阵
题目描述
小 C 正在玩一款排兵布阵的游戏。在游戏中有 n n n 座城堡,每局对战由两名玩家来争夺这些城堡。每名玩家有 m m m 名士兵,可以向第 i i i 座城堡派遣 a i a_i ai 名士兵去争夺这个城堡,使得总士兵数不超过 m m m。
如果一名玩家向第 i i i 座城堡派遣的士兵数严格大于对手派遣士兵数的两倍,那么这名玩家就占领了这座城堡,获得 i i i 分。
现在小 C 即将和其他 s s s 名玩家两两对战,这 s s s 场对决的派遣士兵方案必须相同。小 C 通过某些途径得知了其他 s s s 名玩家即将使用的策略,他想知道他应该使用什么策略来最大化自己的总分。
由于答案可能不唯一,你只需要输出小 C 总分的最大值。
输入格式
输入第一行包含三个正整数 s , n , m s,n,m s,n,m,分别表示除了小 C 以外的玩家人数、城堡数和每名玩家拥有的士兵数。
接下来 s s s 行,每行 n n n 个非负整数,表示一名玩家的策略,其中第 i i i 个数 a i a_i ai 表示这名玩家向第 i i i 座城堡派遣的士兵数。
输出格式
输出一行一个非负整数,表示小 C 获得的最大得分。
样例 #1
样例输入 #1
1 3 10
2 2 6
样例输出 #1
3
样例 #2
样例输入 #2
2 3 10
2 2 6
0 0 0
样例输出 #2
8
提示
样例1解释:
小 C 的最佳策略为向第 1 1 1 座城堡和第 2 2 2 座城堡各派遣 5 5 5 名士兵。
样例2解释:
小 C 的最佳策略之一为向第 1 1 1 座城堡派遣 2 2 2 名士兵,向第 2 2 2 座城堡派遣 5 5 5 名士兵,向第 3 3 3 座城堡派遣 1 1 1 名士兵。
数据范围:
对于 10 % 10\% 10% 的数据: s = 1 , n ≤ 3 , m ≤ 10 s=1,n \le 3,m \le 10 s=1,n≤3,m≤10
对于 20 % 20\% 20% 的数据: s = 1 , n ≤ 10 , m ≤ 100 s=1,n \le 10,m \le 100 s=1,n≤10,m≤100
对于 40 % 40\% 40% 的数据: n ≤ 10 , m ≤ 100 n\le 10,m\le 100 n≤10,m≤100
对于另外 20 % 20\% 20% 的数据: s = 1 s=1 s=1
对于 100 % 100\% 100% 的数据:
1 ≤ s ≤ 100 1\le s \le 100 1≤s≤100
1 ≤ n ≤ 100 1\le n \le 100 1≤n≤100
1 ≤ m ≤ 20000 1\le m \le 20000 1≤m≤20000
对于每名玩家 a i ≥ 0 a_i \ge 0 ai≥0, ∑ i = 1 n a i ≤ m \sum\limits_{i=1}^n a_i \le m i=1∑nai≤m
解题思路
状态定义:dp[i][j]表示前i个城堡派遣j个士兵的最大得分
转移方程:dp[i][j]=max(dp[i-1][j],dp[i-1][j-n]+i*k) (n表示士兵人数,具体值可变,k表示可占领的城堡得数量,n和k的对应关系单独处理)
代码实现
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
#define MAX_S 100
#define MAX_N 100
#define MAX_M 20000
int bing[MAX_S+5][MAX_N+5];
int dp[MAX_N+5][MAX_M+5];
vector<pair<int,int>>g[MAX_N+5];
int s,n,m;
int main()
{cin>>s>>n>>m;for(int i=1;i<=s;i++){for(int j=1;j<=n;j++){cin>>bing[j][i];}}for(int i=1;i<=n;i++)sort(bing[i]+1,bing[i]+1+s);for(int i=1;i<=n;i++){for(int j=1;j<=s;j++){if(bing[i][j]==bing[i][j+1])continue;if(bing[i][j]*2>m)break;g[i].push_back(make_pair(bing[i][j]*2+1,j));}if(bing[i][s]==0)g[i].push_back(make_pair(1,s));}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){dp[i][j]=dp[i-1][j];for(auto k:g[i])if(j>=k.first)dp[i][j]=max(dp[i][j],dp[i-1][j-k.first]+i*k.second);}}cout<<dp[n][m];return 0;
}
总结:背包问题的一般形式为在若干个物品中按照一定的逻辑选择若干个,或者对于每一个物品选择其某一个属性(t4),或者对于某一个物品使用多大的代价选择其多大的部分(t5)等等,以求最后效益最大。
相关文章:

Part 4.2 背包动态规划
->背包模型模板(0/1,分组,完全,多重)<- [NOIP2018 提高组] 货币系统 题目背景 NOIP2018 提高组 D1T2 题目描述 在网友的国度中共有 n n n 种不同面额的货币,第 i i i 种货币的面额为 a [ i ] a[i] a[i],你可以假设每…...
Elasticsearch-使用Logstash同步Mysql
1.安装logstash es服务器版本必须和logstash版本一致 7.9.2 在/usr/local/src/下新建logstash文件夹,解压 下载logstash后查看是否安装成功,在logstash的bin目录下输入指令: ./logstash -e input { stdin { } } output { stdout {} }2.my…...

6.17作业
升级优化自己应用程序的登录界面。 要求: 1. qss实现 2. 需要有图层的叠加 (QFrame) 3. 设置纯净窗口后,有关闭等窗口功能。 4. 如果账号密码正确,则实现登录界面关闭,另一个应用界面显示。 //发送端头文件…...

算法思想个人总结(结合生活理解)
主要思想: 结合生活和游戏理解思想,先知道什么场景用什么算法,然后再理解就能记住 遇到问题可以考虑选择使用,这样才是学活了 https://www.yuque.com/yuqueyonghu5znoyv/ifb5ga/nfcvg3ft9ryuqeem?singleDoc# 《元启发式算法》...

openh264 帧间预测编码过程源码分析
openh264 OpenH264 是一个开源的 H.264 编码和解码器,由思科系统开发并维护。它专为实时应用程序如 WebRTC 设计,提供了从基础到高级特性的广泛支持。OpenH264 的编码器支持从 Constrained Baseline Profile 到 5.2 级别,允许任意分辨率的编…...
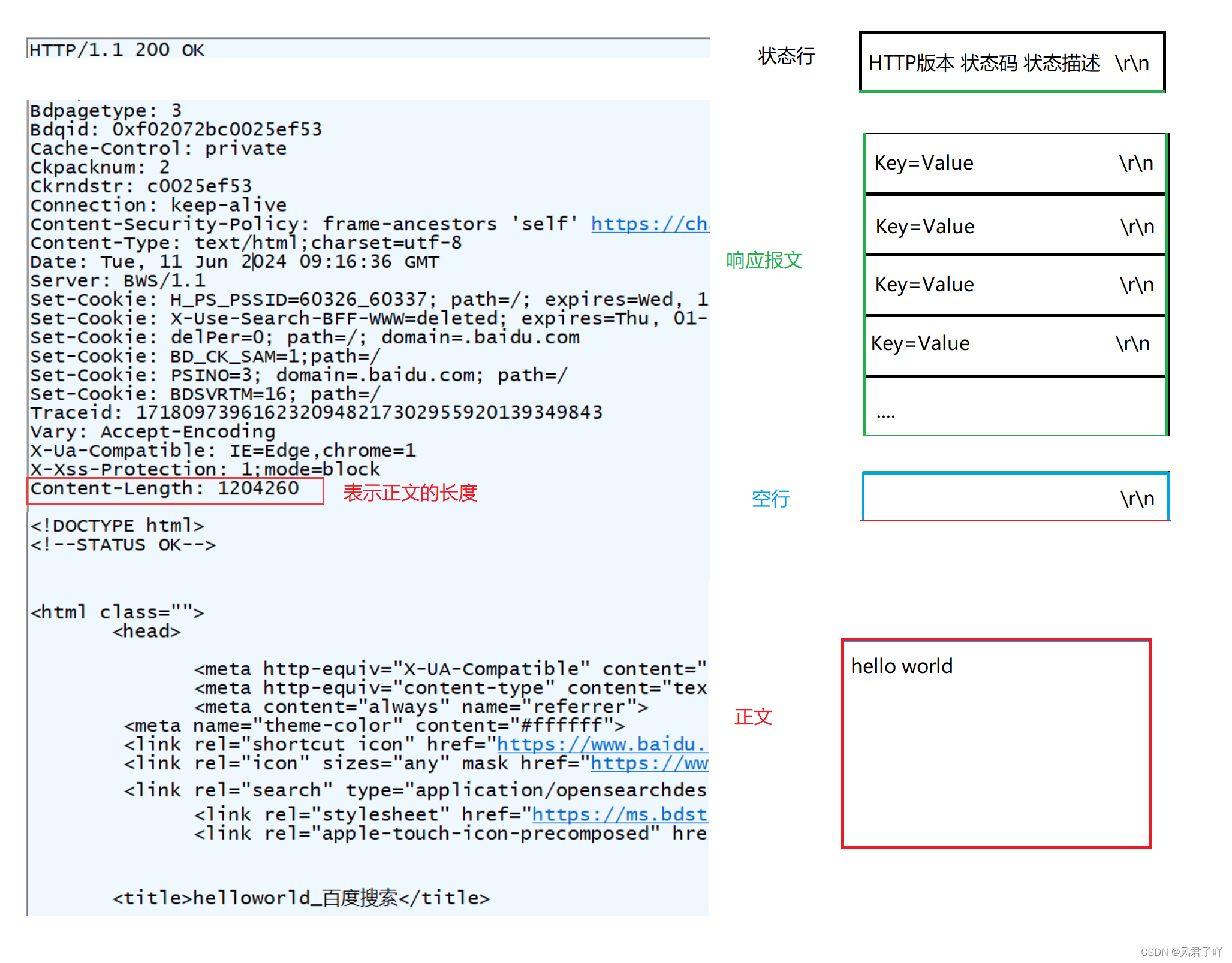
Linux网络 - HTTP协议
文章目录 前言一、HTTP协议1.urlurl特殊字符 requestrespond 总结 前言 上一章内容我们讲了在应用层制定了我们自己自定义的协议、序列化和反序列化。 协议的制定相对来讲还是比较麻烦的,不过既然应用层的协议制定是必要的,那么肯定已经有许多计算机大佬…...

面试题——Nginx
1.Nginx是什么? 是一个高性能的Web服务器和反向代理服务器,也可以作为静态文件的缓存服务器,也能够进行负载均衡。 2.Nginx的作用? 1.反向代理:将多台服务器代理为一台服务器。客户端不了解底层服务端。 2.负载均衡…...
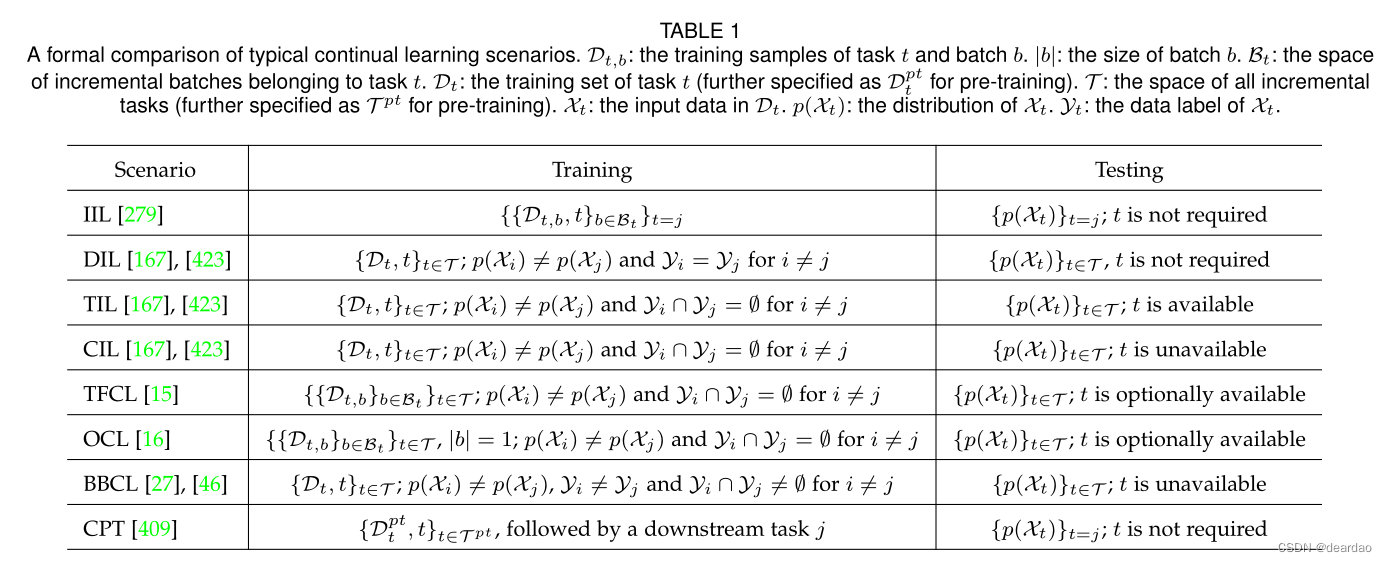
持续学习的综述: 理论、方法与应用
摘要 为了应对现实世界的动态,智能系统需要在其整个生命周期中增量地获取、更新、积累和利用知识。这种能力被称为持续学习,为人工智能系统自适应发展提供了基础。从一般意义上讲,持续学习明显受到灾难性遗忘的限制,在这种情况下…...
问题与解决方案)
跨域资源共享(CORS)问题与解决方案
跨域资源共享(CORS,Cross-Origin Resource Sharing)是现代web开发中常见且重要的一个概念。它涉及到浏览器的同源策略(Same-Origin Policy),该策略用于防止恶意网站从不同来源窃取数据。然而,在…...

实用软件分享-----一款免费的人工智能替换face的神器
专栏介绍:本专栏主要分享一些实用的软件(Po Jie版); 声明1:软件不保证时效性;只能保证在写本文时,该软件是可用的;不保证后续时间该软件能一直正常运行;不保证没有bug;如果软件不可用了,我知道后会第一时间在题目上注明(已失效)。介意者请勿订阅。 声明2:本专栏的…...

不可思议!这款 Python 库竟然能自动生成GUI界面:MagicGUI
目录 什么是MagicGUI? 编辑 MagicGUI的工作原理 安装MagicGUI 创建你的第一个GUI 编辑 其他案例 输入值对话框 大家好,今天我们来聊一聊一个非常有趣且实用的Python库——MagicGUI。这个库可以让你用最少的代码,快速创建图形用户…...
论文发表CN期刊《高考》是什么级别的刊物?
论文发表CN期刊《高考》是什么级别的刊物? 《高考》是由吉林省长春出版社主管并主办的省级教育类期刊,期刊以科教兴国战略为服务宗旨,专门反映和探索国内外教育教学和科研实践的最新成果。该期刊致力于为广大教育工作者提供一个高质量的学术…...

离散数学复习
1.关系的介绍和性质 (1)序偶和笛卡尔积 两个元素按照一定的顺序组成的二元组就是序偶,使用尖括号进行表示,尖括号里面的元素一般都是有顺序的; 笛卡尔积就是有两个集合,从第一个集合里面选择一个元素&am…...

华为网络设备高频命令
1.system-view • 用法:在用户视图下执行 system-view 命令。 • 作用:进入系统视图,以便进行配置性的操作。 • 场景:当需要对设备进行系统级的配置时。 2.sysname XXX • 用法:执行 [Huawei]sysname XXX 命令。…...

信友队:南风的收集
C. [202406C]楠枫的收集 文件操作 时间限制: 1000ms 空间限制: 262144KB 输入文件名: 202406C.in 输出文件名: 202406C.out Accepted 100 分 题目描述 一年四季,寒暑交替,楠枫总是会收集每一个季节的树叶,并把它们制作成标本收集起来。当…...
)
找工作小项目:day16-重构核心库、使用智能指针(3)
day16-重构核心库、使用智能指针(3) 最后将使用这个库的方式进行展示。 1、客户端 在while ((o getopt(argc, argv, optstring)) ! -1)所有的操作都是获取参数的操作,threads 、msgs 和wait 分别指线程数、消息长度以及等待时间。 创建一…...
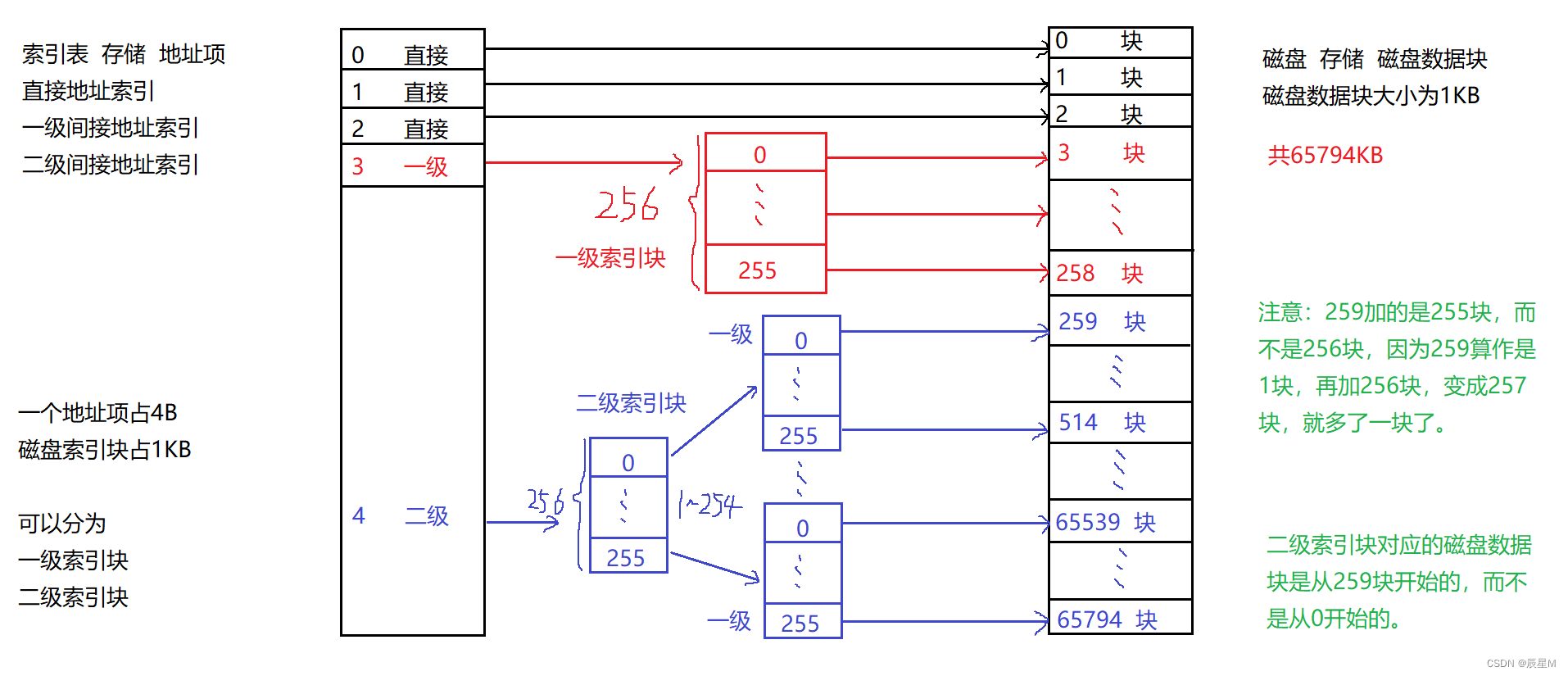
软考中级|软件设计师-知识点整理
目录 计算机网络概论 计算机系统基础知识 中央处理单元 数据表示 校验码 计算机体系结构 计算机体系结构的发展 存储系统 输入/输出技术 安全性、可靠性与系统性能评测基础知识 加密技术和认证技术 计算机可靠性 程序设计语言基础知识 程序设计语言概述 程序设计…...

HTML5基础
1 HTML基础概念(难点) WWW(World Wide Web,万维网)是一种建立在 Internet 上的信息资源网络。 WWW 有 3 个基本组成部分,分别是 URL:Universal Resource Locators,统一资源定位器 HT…...

python,ipython 和 jupyter notebook 之间的关系
python,ipython 和 jupyter notebook 之间的关系 文章目录 python,ipython 和 jupyter notebook 之间的关系1. Python2. IPython3. Jupyter Notebook启动 Jupyter Notebook 关系总结 Python、IPython 和 Jupyter Notebook 是相互关联但具有不同功能的工具…...
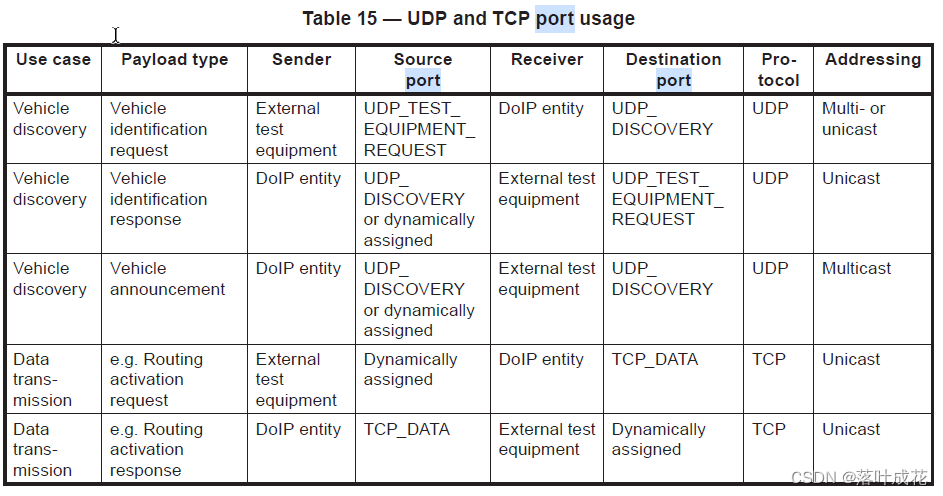
聊聊DoIP吧(三)-端口号port
DoIP在UDP和TCP建立连接和发送诊断报文的过程中使用的端口定义如下:...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
