人工智能实验一:使用搜索算法实现罗马尼亚问题的求解
1.任务描述
本关任务:
- 了解有信息搜索策略的算法思想;
- 能够运用计算机语言实现搜索算法;
- 应用
A*搜索算法解决罗马尼亚问题;
2.相关知识
A*搜索
- 算法介绍
A*算法常用于 二维地图路径规划,算法所采用的启发式搜索可以利用实际问题所具备的启发式信息来指导搜索,从而减少搜索范围,控制搜索规模,降低实际问题的复杂度。
- 算法原理:
A*算法的原理是设计一个代价估计函数:其中 **评估函数F(n)**是从起始节点通过节点n的到达目标节点的最小代价路径的估计值,函数G(n)是从起始节点到n节点的已走过路径的实际代价,函数H(n)是从n节点到目标节点可能的最优路径的估计代价 。
函数 H(n)表明了算法使用的启发信息,它来源于人们对路径规划问题的认识,依赖某种经验估计。根据 F(n)可以计算出当前节点的代价,并可以对下一次能够到达的节点进行评估。
采用每次搜索都找到代价值最小的点再继续往外搜索的过程,一步一步找到最优路径。
3.编程要求
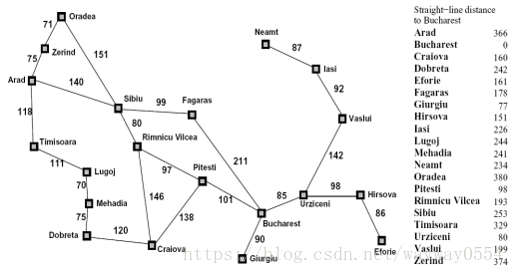
罗马尼亚问题:agent在罗马尼亚度假,目前位于 Arad 城市。agent明天有航班从Bucharest 起飞,不能改签退票。
现在你需要寻找到 Bucharest 的最短路径,在右侧编辑器补充void A_star(int goal,node &src,Graph &graph)函数,使用编写的搜索算法代码求解罗马尼亚问题:
4.测试说明
平台会对你编写的代码进行测试:
预期输出:
solution: 0-> 15-> 14-> 13-> 1-> end
cost:418
5.实验过程
下面是关于非补充部分的代码解释:
1.宏定义每个城市名和编号
#define A 0
#define B 1
#define C 2
#define D 3
#define E 4
#define F 5
#define G 6
#define H 7
#define I 8
#define L 9
#define M 10
#define N 11
#define O 12
#define P 13
#define R 14
#define S 15
#define T 16
#define U 17
#define V 18
#define Z 19
2.记录启发函数h数组,即从n节点到目标节点可能的最优路径的估计代价
int h[20] =//从n节点到目标节点可能的最优路径的估计代价
{ 366,0,160,242,161,
178,77,151,226,244,
241,234,380,98,193,
253,329,80,199,374 };
3.定义城市节点的结构体
struct node
{int g; //从起始节点到n节点的已走过路径的实际代价int h; //从n节点到目标节点可能的最优路径的估计代价int f; //代价估计函数int name;node(int name, int g, int h) { //构造函数this->name = name;this->g = g;this->h = h;this->f = g + h;};//重载运算符bool operator <(const node& a)const { return f < a.f; }
};
4.定义图结构,记录图中各节点和边的信息
class Graph //图结构
{
public:Graph() {memset(graph, -1, sizeof(graph)); //图初始化为-1,代表无边}int getEdge(int from, int to) { //获取边的开销return graph[from][to];}void addEdge(int from, int to, int cost) { //新增一条边及其开销if (from >= 20 || from < 0 || to >= 20 || to < 0)return;graph[from][to] = cost;}void init() { //图初始化addEdge(O, Z, 71);addEdge(Z, O, 71);addEdge(O, S, 151);addEdge(S, O, 151);addEdge(Z, A, 75);addEdge(A, Z, 75);addEdge(A, S, 140);addEdge(S, A, 140);addEdge(A, T, 118);addEdge(T, A, 118);addEdge(T, L, 111);addEdge(L, T, 111);addEdge(L, M, 70);addEdge(M, L, 70);addEdge(M, D, 75);addEdge(D, M, 75);addEdge(D, C, 120);addEdge(C, D, 120);addEdge(C, R, 146);addEdge(R, C, 146);addEdge(S, R, 80);addEdge(R, S, 80);addEdge(S, F, 99);addEdge(F, S, 99);addEdge(F, B, 211);addEdge(B, F, 211);addEdge(P, C, 138);addEdge(C, P, 138);addEdge(R, P, 97);addEdge(P, R, 97);addEdge(P, B, 101);addEdge(B, P, 101);addEdge(B, G, 90);addEdge(G, B, 90);addEdge(B, U, 85);addEdge(U, B, 85);addEdge(U, H, 98);addEdge(H, U, 98);addEdge(H, E, 86);addEdge(E, H, 86);addEdge(U, V, 142);addEdge(V, U, 142);addEdge(I, V, 92);addEdge(V, I, 92);addEdge(I, N, 87);addEdge(N, I, 87);}private:int graph[20][20]; //图数组,用来保存图信息,最多有20个节点
};
5.一些数据结构的定义
bool list[20]; //用于记录节点i是否在openList集合中
vector<node> openList; //扩展节点集合
bool closeList[20]; //已访问节点集合
stack<int> road; //路径
int parent[20]; //父节点,用于回溯构造路径
1.补充void A_star(int goal, node& src, Graph& graph)函数
主要思想是利用一个估价函数f(n)来评估每个节点n的优先级,f(n)由两部分组成:g(n)表示从起点到节点n的实际代价,h(n)表示从节点n到终点的预估代价。A*算法每次选择f(n)最小的节点进行扩展,直到找到终点或者没有可扩展的节点为止
代码如下:
void A_star(int goal, node& src, Graph& graph)//A*搜索算法
{openList.push_back(src); //扩展集合加入起始节点sort(openList.begin(), openList.end()); //排序扩展集合的节点,以取出代价最小的节点while (!openList.empty()){/********** Begin **********/node curNode = openList[0]; //取出扩展集合第一个节点,即代价最小的节点if (curNode.name == goal) { //如果当前节点就是目标节点,则退出return;}openList.erase(openList.begin()); //将当前节点从扩展列表中删除closeList[curNode.name] = true; //将当前节点加入已访问节点list[curNode.name] = false; //标记当前节点已不在扩展集合中for (int i = 0; i < 20; i++) { //开始扩展当前节点,即找到其邻居节点if (graph.getEdge(i, curNode.name) == -1) { //若不是当前节点的邻居节点,跳到下一个节点continue;}if (closeList[i]) { //若此节点已加入已访问集合closeList,也跳到下一个节点continue;}int g1 = curNode.g + graph.getEdge(i, curNode.name); //计算起始节点到当前节点i的g值int h1 = h[i]; //获得当前节点i的h值if (list[i]) { //如果节点i在openList中for (int j = 0; j < openList.size(); j++) {if (i == openList[j].name) { //首先找到节点i的位置,即jif (g1 < openList[j].g) { //如果新的路径的花销更小,则更新openList[j].g = g1;openList[j].f = g1 + openList[j].h;parent[i] = curNode.name; //记录父节点break;}}}}else { //如果节点i不在openList,则将其加入其中(因为扩展时访问了它)node newNode(i, g1, h1); //创建新节点,其参数已知openList.push_back(newNode); //新节点加入openList中parent[i] = curNode.name; //记录父节点list[i] = true; //记录节点i加入了openList}}sort(openList.begin(), openList.end()); //扩展完当前节点后要对openList重新排序/********** End **********/}
}
首先扩展起始节点,将扩展集合中的节点按照优先级进行排序。接着按照优先级不断扩展扩展集合中的节点,直到找到终点或者没有可扩展的节点为止。
每次扩展首先取出扩展集合第一个节点,判断其是否为目标节点,若是则退出。扩展该节点后需要将其加入已访问集合,并从扩展集合中删除,同时用list数组标记其已扩展。
接着扩展该节点,即寻找其邻居节点。
如果邻居节点在扩展集合中,则查看其更新后代价是否比原本的代价更优,优则更新它。同时记录父节点以用于回溯生成路径
如果邻居节点不在扩展集合中,则将其加入扩展集合中,记录父节点,并用list数组标记为在扩展集合中
每次扩展完节点后都要对扩展集合里的节点进行一次优先级的排序,用于下一个循环来取出当前优先级最高的节点
6.void print_result(Graph& graph)函数
用于打印路径和开销
void print_result(Graph& graph) //用于打印路径和开销
{int p = openList[0].name; //p即为目标节点int lastNodeNum;road.push(p); //目标节点压入栈中,之后最后才输出while (parent[p] != -1) //不断回溯获得一条完整路径{road.push(parent[p]);p = parent[p];}lastNodeNum = road.top(); //起始节点int cost = 0; //总开销cout << "solution: ";while (!road.empty()) //栈不为空就继续循环{cout << road.top() << "-> ";if (road.top() != lastNodeNum) //如果栈顶元素不是终点{cost += graph.getEdge(lastNodeNum, road.top()); //添加花销lastNodeNum = road.top(); //更新栈顶元素}road.pop(); //弹出栈顶元素}cout << "end" << endl;cout << "cost:" << cost;
}
6.完整代码
#include<iostream>
#include<vector>
#include<memory.h>
#include<stack>
#include<algorithm>#define A 0
#define B 1
#define C 2
#define D 3
#define E 4
#define F 5
#define G 6
#define H 7
#define I 8
#define L 9
#define M 10
#define N 11
#define O 12
#define P 13
#define R 14
#define S 15
#define T 16
#define U 17
#define V 18
#define Z 19using namespace std;int h[20] =//从n节点到目标节点可能的最优路径的估计代价
{ 366,0,160,242,161,
178,77,151,226,244,
241,234,380,98,193,
253,329,80,199,374 };/*
*一个节点结构,node
*/
struct node
{int g; //从起始节点到n节点的已走过路径的实际代价int h; //从n节点到目标节点可能的最优路径的估计代价int f; //代价估计函数int name;node(int name, int g, int h) { //构造函数this->name = name;this->g = g;this->h = h;this->f = g + h;};//重载运算符bool operator <(const node& a)const { return f < a.f; }
};class Graph //图结构
{
public:Graph() {memset(graph, -1, sizeof(graph)); //图初始化为-1,代表无边}int getEdge(int from, int to) { //获取边的开销return graph[from][to];}void addEdge(int from, int to, int cost) { //新增一条边及其开销if (from >= 20 || from < 0 || to >= 20 || to < 0)return;graph[from][to] = cost;}void init() { //图初始化addEdge(O, Z, 71);addEdge(Z, O, 71);addEdge(O, S, 151);addEdge(S, O, 151);addEdge(Z, A, 75);addEdge(A, Z, 75);addEdge(A, S, 140);addEdge(S, A, 140);addEdge(A, T, 118);addEdge(T, A, 118);addEdge(T, L, 111);addEdge(L, T, 111);addEdge(L, M, 70);addEdge(M, L, 70);addEdge(M, D, 75);addEdge(D, M, 75);addEdge(D, C, 120);addEdge(C, D, 120);addEdge(C, R, 146);addEdge(R, C, 146);addEdge(S, R, 80);addEdge(R, S, 80);addEdge(S, F, 99);addEdge(F, S, 99);addEdge(F, B, 211);addEdge(B, F, 211);addEdge(P, C, 138);addEdge(C, P, 138);addEdge(R, P, 97);addEdge(P, R, 97);addEdge(P, B, 101);addEdge(B, P, 101);addEdge(B, G, 90);addEdge(G, B, 90);addEdge(B, U, 85);addEdge(U, B, 85);addEdge(U, H, 98);addEdge(H, U, 98);addEdge(H, E, 86);addEdge(E, H, 86);addEdge(U, V, 142);addEdge(V, U, 142);addEdge(I, V, 92);addEdge(V, I, 92);addEdge(I, N, 87);addEdge(N, I, 87);}private:int graph[20][20]; //图数组,用来保存图信息,最多有20个节点
};bool list[20]; //用于记录节点i是否在openList集合中
vector<node> openList; //扩展节点集合
bool closeList[20]; //已访问节点集合
stack<int> road; //路径
int parent[20]; //父节点,用于回溯构造路径void A_star(int goal, node& src, Graph& graph)//A*搜索算法
{openList.push_back(src); //扩展集合加入起始节点sort(openList.begin(), openList.end()); //排序扩展集合的节点,以取出代价最小的节点while (!openList.empty()){/********** Begin **********/node curNode = openList[0]; //取出扩展集合第一个节点,即代价最小的节点if (curNode.name == goal) { //如果当前节点就是目标节点,则退出return;}openList.erase(openList.begin()); //将当前节点从扩展列表中删除closeList[curNode.name] = true; //将当前节点加入已访问节点list[curNode.name] = false; //标记当前节点已不在扩展集合中for (int i = 0; i < 20; i++) { //开始扩展当前节点,即找到其邻居节点if (graph.getEdge(i, curNode.name) == -1) { //若不是当前节点的邻居节点,跳到下一个节点continue;}if (closeList[i]) { //若此节点已加入已访问集合closeList,也跳到下一个节点continue;}int g1 = curNode.g + graph.getEdge(i, curNode.name); //计算起始节点到当前节点i的g值int h1 = h[i]; //获得当前节点i的h值if (list[i]) { //如果节点i在openList中for (int j = 0; j < openList.size(); j++) {if (i == openList[j].name) { //首先找到节点i的位置,即jif (g1 < openList[j].g) { //如果新的路径的花销更小,则更新openList[j].g = g1;openList[j].f = g1 + openList[j].h;parent[i] = curNode.name; //记录父节点break;}}}}else { //如果节点i不在openList,则将其加入其中(因为扩展时访问了它)node newNode(i, g1, h1); //创建新节点,其参数已知openList.push_back(newNode); //新节点加入openList中parent[i] = curNode.name; //记录父节点list[i] = true; //记录节点i加入了openList}}sort(openList.begin(), openList.end()); //扩展完当前节点后要对openList重新排序/********** End **********/}
}void print_result(Graph& graph) //用于打印路径和开销
{int p = openList[0].name; //p即为目标节点int lastNodeNum;road.push(p); //目标节点压入栈中,之后最后才输出while (parent[p] != -1) //不断回溯获得一条完整路径{road.push(parent[p]);p = parent[p];}lastNodeNum = road.top(); //起始节点int cost = 0; //总开销cout << "solution: ";while (!road.empty()) //栈不为空就继续循环{cout << road.top() << "-> ";if (road.top() != lastNodeNum) //如果栈顶元素不是终点{cost += graph.getEdge(lastNodeNum, road.top()); //添加花销lastNodeNum = road.top(); //更新栈顶元素}road.pop(); //弹出栈顶元素}cout << "end" << endl;cout << "cost:" << cost;
}int main()
{Graph graph;graph.init();int goal = B; //目标节点Bnode src(A, 0, h[A]); //起始节点Alist[A] = true;memset(parent, -1, sizeof(parent)); //初始化parentmemset(list, false, sizeof(list)); //初始化listA_star(goal, src, graph);print_result(graph);return 0;
}
运行结果:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ukaYZTHr-1678452048946)(C:\Users\86159\AppData\Roaming\Typora\typora-user-images\1678451967482.png)]](https://img-blog.csdnimg.cn/e733b49ffd4b40f4822b78a1c69c29f9.png)
相关文章:

人工智能实验一:使用搜索算法实现罗马尼亚问题的求解
1.任务描述 本关任务: 了解有信息搜索策略的算法思想;能够运用计算机语言实现搜索算法;应用A*搜索算法解决罗马尼亚问题; 2.相关知识 A*搜索 算法介绍 A*算法常用于 二维地图路径规划,算法所采用的启发式搜索可以…...

Spring Security基础入门
基础概念 什么是认证 认证:用户认证就是判断一个用户的身份身份合法的过程,用户去访问系统资源的时候系统要求验证用户的身份信息,身份合法方可继续访问,不合法则拒绝访问。常见的用户身份认证方式有:用户密码登录&am…...

dnsresolver-limit
文件OperationLimiter.h功能DnsResolver是andnroid中提供DNS能力的小型DNS解析器,limit是其中的一个小模块,支持全局、基于key(UID)的DNS请求限制。DnsResolver是多线程模型,单个DNS请求最多启动3个线程(传统DNS)。在网…...

使用 YoctoProject集成Qt6
By Toradex胡珊逢在嵌入式领域中Qt 作为普遍选择的 UI 方案目前已经发布 Qt6 版本。本文将介绍如何为 Toradex 的计算机模块使用 Yocto Project 将 Qt6 集成到镜像里。首先根据这里的说明,准备好Yocto Project 的编译环境。这里我们选择 Toradex 最新的 Linux BSP V…...

「媒体邀约」如何选择适合的媒体公关,媒体服务供应商
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 每天胡老师也会接到大量关于媒体方面的询问,胡老师也都一一的很耐心的进行了解答,也都很详细的做了媒体规划和媒体传播方案,但有的朋友还是很犹豫&…...

html2canvas和jspdf导出pdf,每个页面模块占一页,在pdf中垂直居中显示
需求:html页面转换pdf,页面有多个模块,页面中有文本、echarts、表格等模块,一个模块占一页,因为模块高度不够,所以需要垂直居中 通过html2canvas和jspdf实现,html2canvas用于将页面元素生成canv…...
)
数学小课堂:集合论的公理化过程(用构建公理化体系的思路来构建自然数)
文章目录 引言I 数的理论1.1 构建自然数1.2 定义整数/有理数/实数/虚数/复数II 自然数和集合的关系1.3 集合1.2 构建自然数III 线性规划问题(线性代数+最优化)3.1 题目3.2 答案引言 数学是一个公理化的体系,是数学对其它知识体系有启发的地方。 数学的思维方式: 不轻易相信…...

3.10多线程
一.常见锁策略1.悲观锁 vs乐观锁体现在处理锁冲突的态度①悲观锁:预期锁冲突的概率高所以做的工作更多,付出的成本更多,更低效②乐观锁:预期锁冲突的概率低所以做的工作少,付出的成本更低,更搞笑2.读写锁 vs 普通的互斥锁①普通的互斥锁,只有两个操作 加锁和解锁只有两个线程针…...

缓存双写一致性之更新策略探讨
问题由来 数据redis和MySQL都要有一份,如何保证两边的一致性。 如果redis中有数据:需要和数据库中的值相同如果redis中没有数据:数据库中的值是最新值,且准备会写redis 缓存操作分类 自读缓存读写缓存: ࿰…...

scala高级函数快速掌握
scala高级函数一.函数至简原则二.匿名的简化原则三.高阶函数四.柯里化和闭包五.递归六.抽象控制七.惰性加载🔥函数对于scala(函数式编程语言)来说非常重要,大家一定要学明白,加油!!!…...
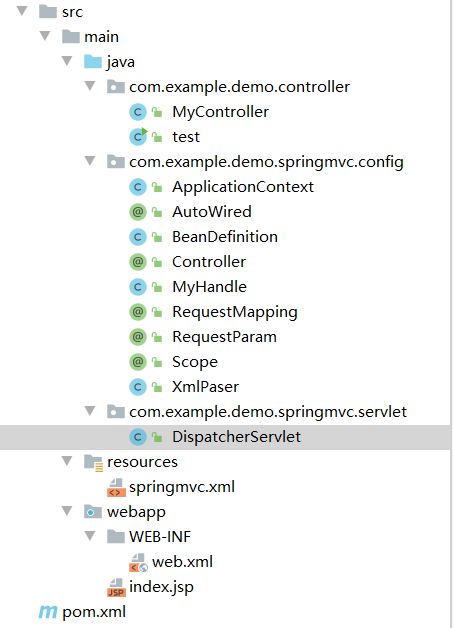
手写模拟SpringMvc源码
MVC框架MVC是一种设计模式(设计模式就是日常开发中编写代码的一种好的方法和经验的总结)。模型(model)-视图(view)-控制器(controller),三层架构的设计模式。用于实现前端…...
五分钟了解JumpServer V2.* 与 v3 的区别
一、升级注意项 1、梳理数据。JumpServer V3 去除了系统用户功能,将资产与资产直接绑定。当一个资产名下有多个同名账号,例如两个root用户时,升级后会自动合并最后一个root,不会同步其他root用户。升级前需保证每一个资产只拥有一…...

用友开发者中心应用构建实践指引!
基于 iuap 技术底座,用友开发者中心致力于为企业和开发者提供一站式技术服务,让人人都能轻松构建企业级应用。 本文以人力资源领域常用的应聘人员信息登记与分析功能为例,详细介绍如何在用友开发者中心使用 YonBuilder 进行应用构建。 功能…...
snap使用interface:content的基础例子
snap做包还在学习阶段,官网文档可查看:The content interface | Snapcraft documentation该例子由publiser和consumer两部分组成,一个提供一个只读的数据区,一个来进行读取其中的信息,这样就完成了content的交互。publ…...

蓝桥杯刷题第七天
第一题:三角回文数问题描述对于正整数 n, 如果存在正整数 k 使得2n123⋯k2k(k1), 则 n 称为三角数。例如, 66066 是一个三角数, 因为 66066123⋯363。如果一个整数从左到右读出所有数位上的数字, 与从右到左读出所有数位 上的数字是一样的, 则称这个数为回文数。例如…...

FinOps首次超越安全成为企业头等大事|云计算趋势报告
随着云计算在过去十年中的广泛应用,云计算用户所面临的一个持续不变的趋势是:安全一直是用户面临的首要挑战。然而,这种情况正在发生转变。 知名IT软件企业 Flexera 对云计算决策者进行年度调研已经持续12年,而今年安全问题首次…...
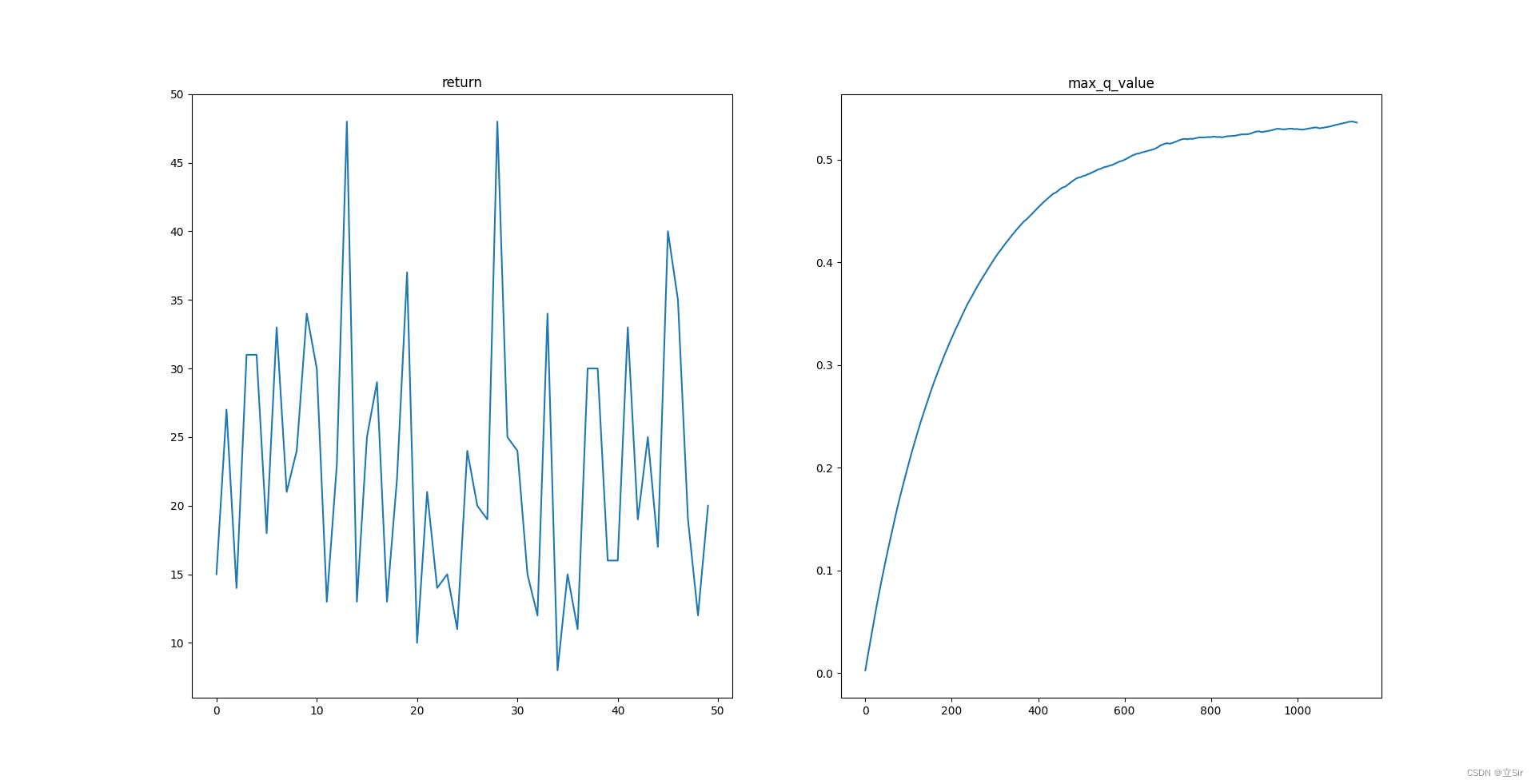
【深度强化学习】(3) Policy Gradients 模型解析,附Pytorch完整代码
大家好,今天和各位分享一下基于策略的深度强化学习方法,策略梯度法是对策略进行建模,然后通过梯度上升更新策略网络的参数。我们使用了 OpenAI 的 gym 库,基于策略梯度法完成了一个小游戏。完整代码可以从我的 GitHub 中获得&…...
Windows基于Nginx搭建RTMP流媒体服务器(附带所有组件下载地址及验证方法)
RTMP服务时常用于直播时提供拉流推流传输数据的一种服务。前段时间由于朋友想搭建一套直播时提供稳定数据传输的服务器,所以就研究了一下如何搭建及使用。 1、下载nginx 首先我们要知道一般nginx不能直接配置rtmp服务,在Windows系统上需要特殊nginx版本…...
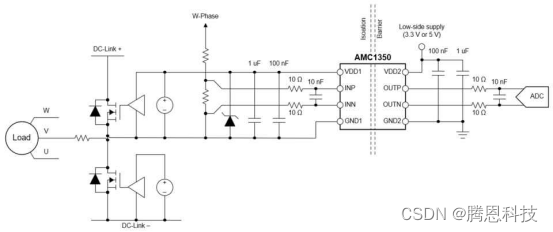
交流电机驱动器中的隔离电压感应
汽车和工业终端设备,如电机驱动器、串式逆变器和机载充电器,在高电压下运行,不能安全地与人直接互动。隔离电压测量通过保护人类免受高压电路执行一个功能的影响,有助于优化操作和确保使用的安全性。 设计用于高性能,隔…...

爬取知乎问题答案
参考博客:基于Python知乎回答爬虫 jieba关键字统计可视化_知乎爬虫搜索关键词_菠萝柚王子的博客-CSDN博客 1、安装依赖包 import numpy import requests import certifi from PIL import Image from lxml import etree import jieba from wordcloud import WordClo…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
