manacher算法详解
例题
- 求一个字符串的最长回文子串的长度
O(N2)O(N^2)O(N2)的解法很容易想,就是从每个字符位置向左右同时拓展,然后检查当前是不是回文,更新长度,可以简单写一下代码
int solve(string &ss){int ans = 0;int n = ss.length();string s;s.resize(2 * n + 1);int l = 0;s[l++] = '$';s[l++] = '#';for(int i=0;i<n;i++){s[l++] = ss[i];s[l++] = '#';}for(int i=0;i<l;i++){int p = 0;while(i - p >= 0 && i + p < l && s[i + p] == s[i - p]){p += 1;}ans = max(ans, p - 1);}return ans;
}
- 这里注意一个小技巧,一个字符串有两种情况,分别是长度为奇数和长度为偶数,如何将这两种情况归一化呢?考虑在字符串前面加一个$,在每两个字符之间放一个#,不一定非得是$和#,只要不会在字符串中出现即可,容易计算得到这样做得到的字符串长度一定是奇数
- 考虑优化,容易想到如果计算已经得到了前面的回文半径(以某个字符为中心的回文串长度的一半),那么对称的两个点中尚未计算的那个点的回文半径的最小值也就是已经计算得到的那个点的回文半径

- 观察上面的字符串,第一个红色的b的回文半径容易求出是2,后面的c的回文半径容易求出是6,那么我们如何根据它求出后面的红色的b的回文半径呢?显然因为c的回文半径范围覆盖了第一个红色的b,所以第二个红色的b的回文半径的最小值是第一个红色的b的回文半径(这里同时因为c的回文半径也覆盖了第二个红色的b的回文半径区域,因为如果第二个红色的b之后没有足够的字符也是到不了第一个红色的b的回文半径的),这样我们就得到了第二个b的回文半径的最小值,然后暴力拓展,就为之后的字符串也做好了铺垫,可以证明总的时间复杂度是O(n)O(n)O(n)的
- 上面是我对manacher算法的个人理解,接下来从代码的角度来说一下,首先需要两个变量
r和c,因为有一个问题,怎么判断某个字符是不是在某个回文区间之内,我们可以从左边递推找到一个右端点最远的回文区域,这样记录一下中心端点c和右端点r,在从左到右计算的过程中更新最大的r,这样就找到了回文半径和回文中心 - 然后使用一个数组
P[i]记录以i为中心的回文半径,具体代码如下
int manacher(string &ss){int n = ss.length();string s;s.resize(2 * n + 1);int l = 0;s[l++] = '$';s[l++] = '#';for(int i=0;i<n;i++){s[l++] = ss[i];s[l++] = '#';}vector<int> P(l);int r, c;r = c = 0;int ans = 0;for(int i=0;i<l;i++){int &p = P[i];// 用r - i约束的原因上面已经说过p = (i + p < r ? min(r - i, P[2 * c - i]) : 1);// 2 * c - i是对称位置的字符while(s[i + p] == s[i - p]) p += 1;if(i + p > r){r = i + p;c = i;}ans = max(ans, p - 1);}return ans;
}
例题
https://www.luogu.com.cn/problem/P4287
在一个字符串里面找前后两个长度相等的子串都是回文串的字符串的最大长度
- 考虑manacher,如果计算出了一个回文串,因为它的前面已经计算好了,比如现在回文半径右端点最远在rrr,那么从iii到rrr这一段是回文串的一半我们是知道的,现在考虑它前面一段,怎么考虑呢?根据对称性,设j≥rj\geq rj≥r,对称到左边就是i−j−i2i-\frac{j-i}{2}i−2j−i同时还需要满足(j−i)%4=0(j-i)\%4=0(j−i)%4=0,这里的iii是右侧字符串的回文中心,jjj是左侧字符串关于ccc对称的回文中心
- 因为要求这样的回文串长度必须是偶数,所以根据我们的回文串构造方法,每次枚举的iii必须是奇数
#include <bits/stdc++.h>using namespace std;int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n;string ss;cin >> n >> ss;string s;s.resize(2 * n + 1);int l = 0;s[l++] = '$';s[l++] = '#';for(int i=0;i<n;i++){s[l++] = ss[i];s[l++] = '#';}vector<int> P(l);int r, c;r = c = 0;int ans = 0;for(int i=0;i<l;i++){int &p = P[i];p = (i + p < r ? min(P[2 * c - i], r - i) : 1);while(s[i + p] == s[i - p]) p += 1;if(i + p > r){if(i & 1){for(int j=max(r, i + 4);j<=i+p;j++){if((j - i) % 4 == 0 && P[i - (j - i) / 2] >= (j - i) / 2){ans = max(ans, j - i);}}}r = i + p;c = i;}}cout << ans << '\n';return 0;
}
相关文章:

manacher算法详解
例题 求一个字符串的最长回文子串的长度 O(N2)O(N^2)O(N2)的解法很容易想,就是从每个字符位置向左右同时拓展,然后检查当前是不是回文,更新长度,可以简单写一下代码 int solve(string &ss){int ans 0;int n ss.length();s…...

要做一个关于DDD的内部技术分享,记录下用到的资源,学习笔记(未完)
最后更新于2023年3月10日 14:28:08 问题建模》软件分层》具体结构,是层层递进的关系。有了问题建模,才能进行具体的软件分层的讨论,再有了分层,才能讨论在domain里面应该怎么实现具体结构。 1、问题建模:Domain、Mod…...

KDZD互感器二次负载测试仪
一、概述 电能计量综合误差过大是电能计量中普遍存在的一个关键问题。电压互感器二次回路压降引起的计量误差往往是影响电能计量综合误差的因素。所谓电压互感器二次压降引起的误差,就是指电压互感器二次端子和负载端子之间电压的幅值差相对于二次实际电压的百分数…...
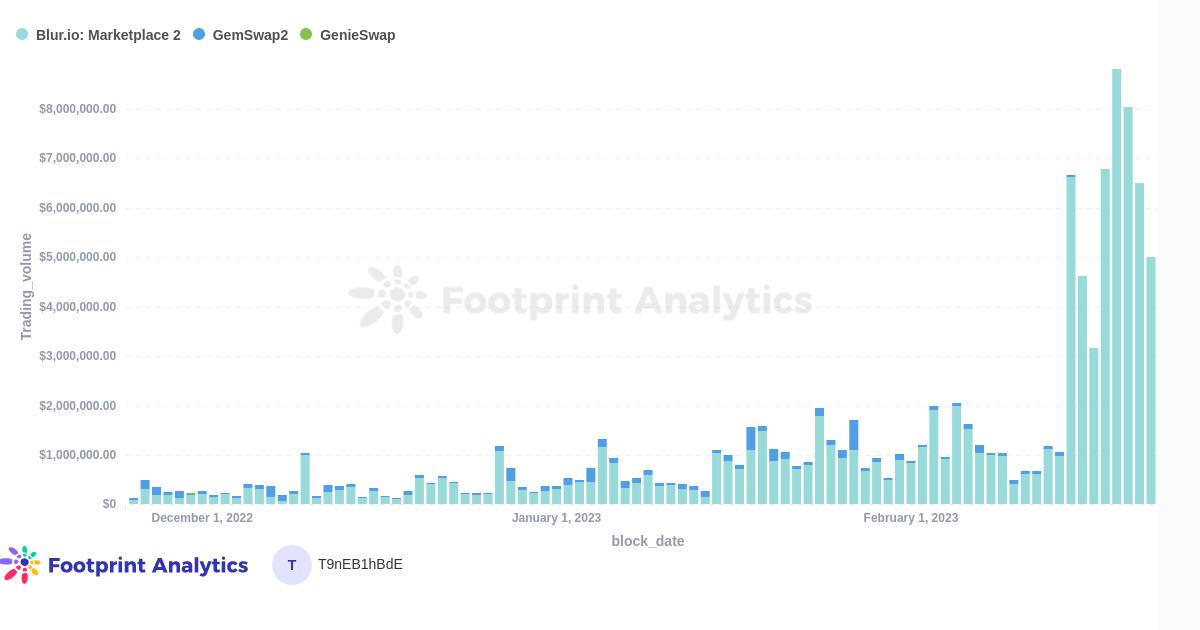
在空投之后,Blur能否颠覆OpenSea的主导地位?
Mar. 2023, Daniel数据源: NFT Aggregators Overview & Aggregator Statistics Overview & Blur Airdrop一年前,通过聚合器进行的NFT交易量开始像滚雪球一样增长,有时甚至超过了直接通过市场平台的交易量。虽然聚合器的使用量从10月到…...
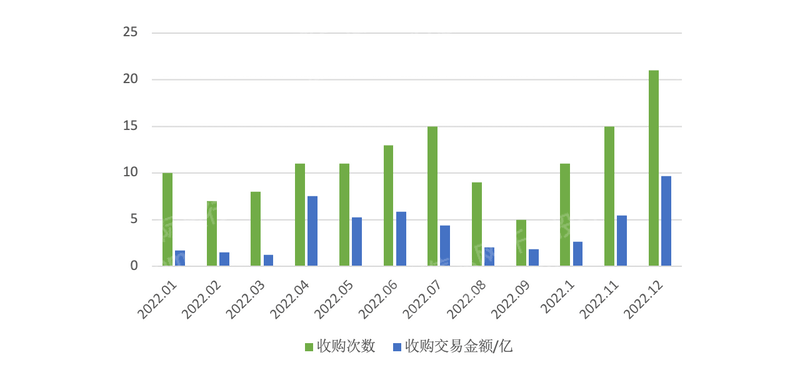
2023年新三板产品及服务研究报告
第一章 概述 全国中小企业股份转让系统(英语:National Equities Exchange and Quotations,缩写NEEQ),简称股转系统,是第三家全国性证券交易场所,因挂牌企业均为高科技企业而不同于原转让系统内…...
张力控制之开环模式
张力控制的相关知识也可以参看专栏的其它文章,链接如下: 张力闭环控制之传感器篇(精密调节气阀应用)_RXXW_Dor的博客-CSDN博客跳舞轮对应张力调节范围,我们可以通过改变气缸的气压方式间接改变,张力跳舞轮在收放卷闭环控制上的详细应用,可以参看下面的文章链接,这里我…...

python的django框架从入门到熟练【保姆式教学】第二篇
在上一篇博客中,我们介绍了Django的基础知识,并创建了一个简单的Web应用程序。在本篇教程中,我们将深入探讨Django的模型层(Model),它是Django应用程序的核心组件之一。 模型层 Django的模型层是一个对象…...
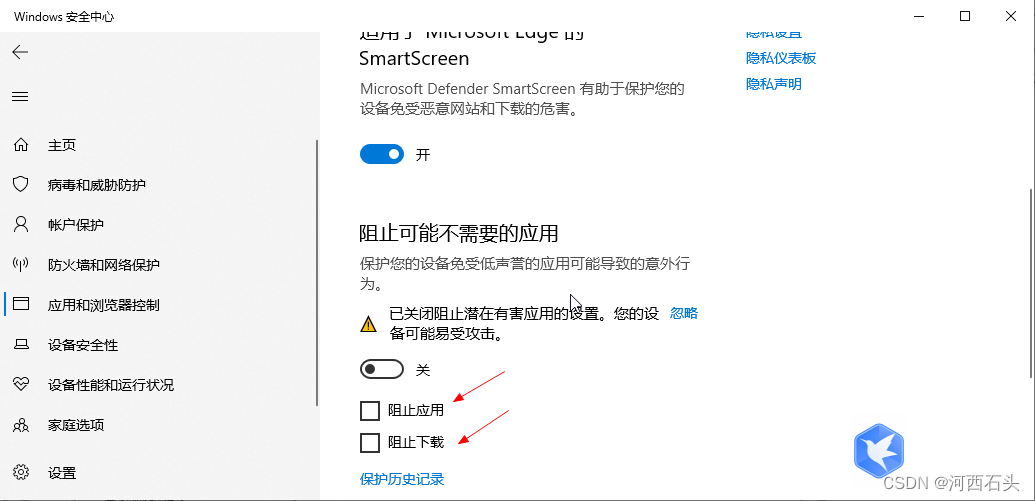
解决win10的过度保护导致文件下载不了程序不能打开运行
win7看来大概是要离我们远去了,虽然我们还能看见她的背影,但大势所趋,我们也只能慢慢的接受win10进入到我们的日常生活。但win10很多时候过度的保护却给我们带来了不便。这里列举两个最常见的问题,当然我这里也给出了解决方案。 文…...

扬帆优配|业务量大突破,这个行业发展明显向好
近期上市的新股,大都在招股阐明书里公布了本年第一季度成绩预告。 我国快递事务量本年已达200亿件 国家邮政局监测数据显现,到3月8日,本年我国快递事务量已到达200.9亿件,比2019年到达200亿件提前了72天,比2022年提前…...
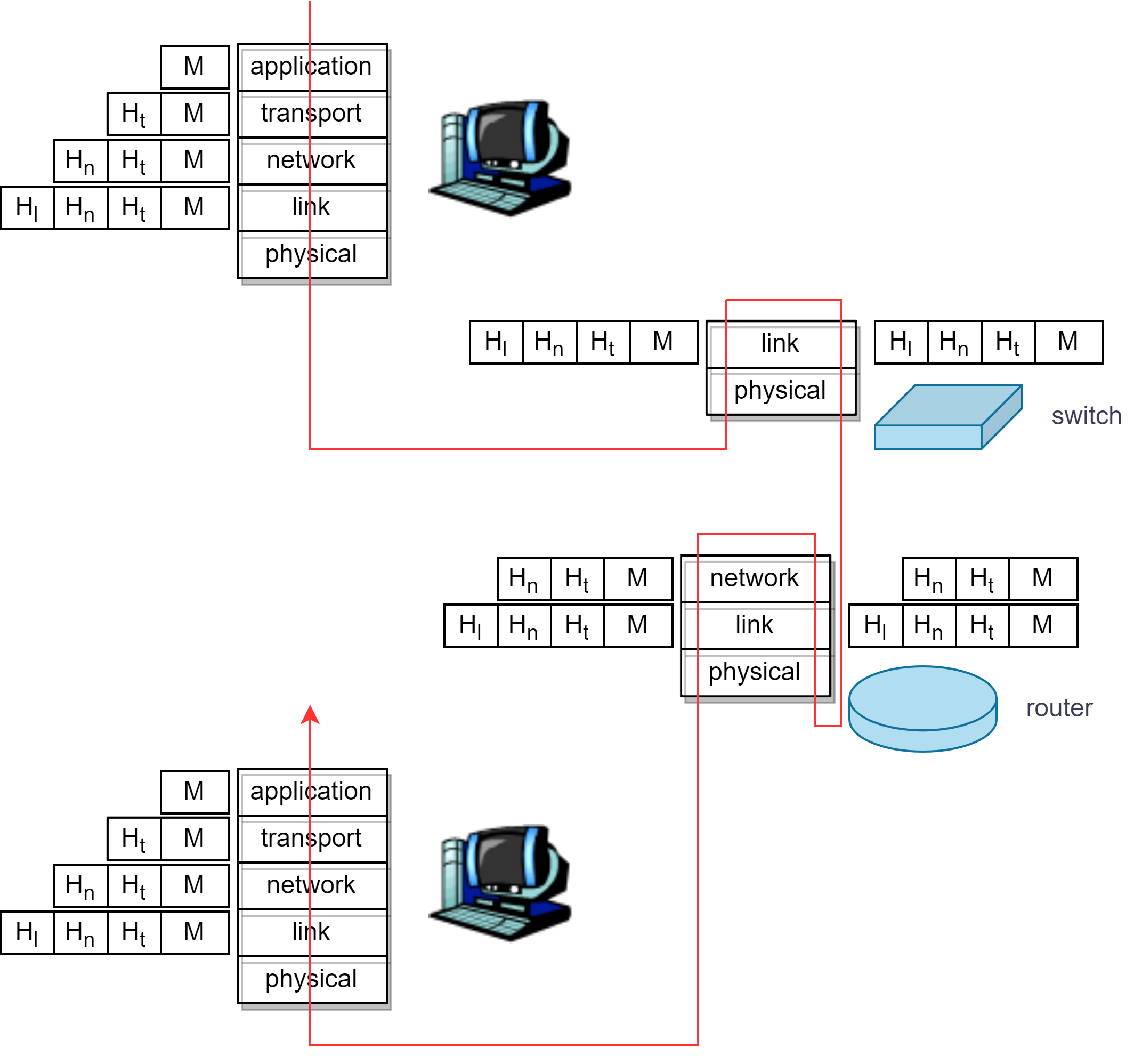
DJ1-4 计算机网络和因特网
目录 一、协议层及其服务模型 ISO/OSI 七层参考模型 TCP/IP 参考模型 1. 网际协议栈(protocol stack) 2. 分层:逻辑通信 3. 协议分层与数据 二、攻击威胁下的网络 1. 植入恶意软件 2. 攻击服务器和网络基础设施 3. 嗅探分组 4. 伪…...

Nginx根据$host及请求的URI规则重定向rewrite
项目背景: 将域名请求从默认的80端口转发到443 ssl。本项目特殊之处是一个端口监听多个域名,某些域名还有跳转到特定的地址。 普通情况: server { listen 80; #默认的80端口,非…...

人工智能实验一:使用搜索算法实现罗马尼亚问题的求解
1.任务描述 本关任务: 了解有信息搜索策略的算法思想;能够运用计算机语言实现搜索算法;应用A*搜索算法解决罗马尼亚问题; 2.相关知识 A*搜索 算法介绍 A*算法常用于 二维地图路径规划,算法所采用的启发式搜索可以…...

Spring Security基础入门
基础概念 什么是认证 认证:用户认证就是判断一个用户的身份身份合法的过程,用户去访问系统资源的时候系统要求验证用户的身份信息,身份合法方可继续访问,不合法则拒绝访问。常见的用户身份认证方式有:用户密码登录&am…...

dnsresolver-limit
文件OperationLimiter.h功能DnsResolver是andnroid中提供DNS能力的小型DNS解析器,limit是其中的一个小模块,支持全局、基于key(UID)的DNS请求限制。DnsResolver是多线程模型,单个DNS请求最多启动3个线程(传统DNS)。在网…...

使用 YoctoProject集成Qt6
By Toradex胡珊逢在嵌入式领域中Qt 作为普遍选择的 UI 方案目前已经发布 Qt6 版本。本文将介绍如何为 Toradex 的计算机模块使用 Yocto Project 将 Qt6 集成到镜像里。首先根据这里的说明,准备好Yocto Project 的编译环境。这里我们选择 Toradex 最新的 Linux BSP V…...

「媒体邀约」如何选择适合的媒体公关,媒体服务供应商
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 每天胡老师也会接到大量关于媒体方面的询问,胡老师也都一一的很耐心的进行了解答,也都很详细的做了媒体规划和媒体传播方案,但有的朋友还是很犹豫&…...

html2canvas和jspdf导出pdf,每个页面模块占一页,在pdf中垂直居中显示
需求:html页面转换pdf,页面有多个模块,页面中有文本、echarts、表格等模块,一个模块占一页,因为模块高度不够,所以需要垂直居中 通过html2canvas和jspdf实现,html2canvas用于将页面元素生成canv…...
)
数学小课堂:集合论的公理化过程(用构建公理化体系的思路来构建自然数)
文章目录 引言I 数的理论1.1 构建自然数1.2 定义整数/有理数/实数/虚数/复数II 自然数和集合的关系1.3 集合1.2 构建自然数III 线性规划问题(线性代数+最优化)3.1 题目3.2 答案引言 数学是一个公理化的体系,是数学对其它知识体系有启发的地方。 数学的思维方式: 不轻易相信…...

3.10多线程
一.常见锁策略1.悲观锁 vs乐观锁体现在处理锁冲突的态度①悲观锁:预期锁冲突的概率高所以做的工作更多,付出的成本更多,更低效②乐观锁:预期锁冲突的概率低所以做的工作少,付出的成本更低,更搞笑2.读写锁 vs 普通的互斥锁①普通的互斥锁,只有两个操作 加锁和解锁只有两个线程针…...

缓存双写一致性之更新策略探讨
问题由来 数据redis和MySQL都要有一份,如何保证两边的一致性。 如果redis中有数据:需要和数据库中的值相同如果redis中没有数据:数据库中的值是最新值,且准备会写redis 缓存操作分类 自读缓存读写缓存: ࿰…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

Linux【5】-----编译和烧写Linux系统镜像(RK3568)
参考:讯为 1、文件系统 不同的文件系统组成了:debian、ubuntu、buildroot、qt等系统 每个文件系统的uboot和kernel是一样的 2、源码目录介绍 目录 3、正式编译 编译脚本build.sh 帮助内容如下: Available options: uboot …...

安全领域新突破:可视化让隐患无处遁形
在安全领域,隐患就像暗处的 “幽灵”,随时可能引发严重事故。传统安全排查手段,常常难以将它们一网打尽。你是否好奇,究竟是什么神奇力量,能让这些潜藏的隐患无所遁形?没错,就是可视化技术。它如…...

2025年全国I卷数学压轴题解答
第19题第3问: b b b 使得存在 t t t, 对于任意的 x x x, 5 cos x − cos ( 5 x t ) < b 5\cos x-\cos(5xt)<b 5cosx−cos(5xt)<b, 求 b b b 的最小值. 解: b b b 的最小值 b m i n min t max x g ( x , t ) b_{min}\min_{t} \max_{x} g(x,t) bmi…...
