6、while循环 - 习题解析
目录
- 解析部分:
- 分支练习
- 1244. 请问一个正整数能够整除几次2
- 问题描述
- 解题思路
- 代码实现
- 代码解析
- 1062. 求落地次数
- 问题描述
- 解题思路
- 代码实现
- 代码解析
- 1254. 求车速
- 问题描述
- 解题思路
- 代码实现
- 代码解析
- 1261. 韩信点兵
- 问题描述
- 解题思路
- 代码实现
- 代码解析
解析部分:
分支练习
1244. 请问一个正整数能够整除几次2
问题描述
请问一个正整数 𝑛n 能够整除几次 2?
比如: 4 可以整除 2 次 2 ,100 可以整除 50次 2 , 9 可以整除 0 次 2 。
解题思路
- 读入数据: 从标准输入读取一个正整数 𝑛n。
- 计算整除次数:
- 初始化计数器
count为 0。 - 当 𝑛n 为偶数时,重复以下步骤:
- 计数器
count加 1。 - 𝑛n 除以 2,更新 𝑛n 的值。
- 计数器
- 初始化计数器
- 输出结果: 输出计数器
count的值,表示 𝑛n 能够被 2 整除的次数。
代码实现
#include <iostream>
using namespace std;
int main() {int n; // 定义一个整型变量来存储输入的数cin >> n; // 通过标准输入读取这个数int count = 0; // 初始化计数器为0while (n % 2 == 0) { // 当n为偶数时,重复以下步骤count++; // 计数器加1n /= 2; // n除以2,更新n的值}cout << count << endl; // 输出计数器的值,表示n能够被2整除的次数return 0; // 程序结束
}
代码解析
- 使用
cin从标准输入读取一个整数n。 - 初始化计数器
count为0。 - 使用
while循环,当n为偶数时(n % 2 == 0),重复以下步骤:- 计数器
count加1。 n除以2,更新n的值。
- 计数器
- 使用
cout输出计数器count的值,表示n能够被2整除的次数。
问题描述中的例子也进行了修正:
- 4 可以整除 2 次 2
- 100 可以整除 2 次 2
- 9 可以整除 0 次 2
1062. 求落地次数
问题描述
小球从 100 米高处自由落下,着地后又弹回高度的一半再落下。
经过多少次落地后,小球弹起的高度才会低于 0.5 米?
解题思路
- 初始化高度: 将初始高度
height设为 100。 - 计算落地次数:
- 初始化计数器
count为 0。 - 当高度
height大于等于 0.5 时,重复以下步骤:- 计数器
count加 1。 - 高度
height除以 2,更新高度的值。
- 计数器
- 初始化计数器
- 输出结果: 输出计数器
count的值,表示小球落地的次数。
代码实现
#include <iostream>
using namespace std;
int main() {double height = 100; // 初始化高度为100int count = 0; // 初始化计数器为0while (height >= 0.5) { // 当高度大于等于0.5时,重复以下步骤count++; // 计数器加1height /= 2; // 高度除以2,更新高度的值}cout << count << endl; // 输出计数器的值,表示小球落地的次数return 0; // 程序结束
}
代码解析
- 初始化高度
height为100。 - 初始化计数器
count为0。 - 使用
while循环,当高度height大于等于0.5时,重复以下步骤:- 计数器
count加1。 - 高度
height除以2,更新高度的值。
- 计数器
- 使用
cout输出计数器count的值,表示小球落地的次数。
1254. 求车速
问题描述
一辆以固定速度行驶的汽车,司机在上午 10 点看到里程表上的读数是一个对称数(即这个数从左向右读和从右向左读是完全一样的),为 95859 。
两小时后里程表上出现了一个新的对称数。
问该车的速度是多少?新的对称数是多少?
输入
无。
输出
输出两行,第一行是车速,第二行是新的里程数(两个都是整数)。
解题思路
- 确定初始里程: 根据题目描述,初始里程为 95859。
- 寻找下一个对称数:
- 从初始里程开始,依次递增里程数。
- 对于每个里程数,判断它是否为对称数:
- 取出里程数的万位、千位、十位、个位。
- 判断万位与个位是否相等,千位与十位是否相等。
- 当找到下一个对称数时,停止寻找。
- 计算车速:
- 下一个对称数与初始里程的差值即为两小时内行驶的里程。
- 将里程差除以 2,得到车速(单位为千米/小时)。
- 输出结果: 输出两行,第一行为车速,第二行为新的对称数里程。
代码实现
#include<iostream>
#include<iomanip>
using namespace std;
int main()
{ int n = 95859; // 初始里程int n2 = 95859; // 保存初始里程的副本while(true) // 无限循环,直到找到下一个对称数{n++; // 里程数加1int g = n%10; // 取个位int s = n/10%10; // 取十位int q = n/1000%10; // 取千位int w = n/10000%10; // 取万位if(w==g && q==s) // 如果万位与个位相等,千位与十位相等,则为对称数{break; // 跳出循环}}cout<<(n-n2)/2<<endl; // 输出车速cout<<n<<endl; // 输出新的对称数里程return 0;
}
代码解析
- 初始化初始里程
n为95859,并复制一份到n2。 - 使用无限循环
while(true),直到找到下一个对称数为止。 - 里程数
n加1,继续寻找。 - 取出里程数的个位
g、十位s、千位q、万位w。 - 判断万位
w与个位g是否相等,千位q与十位s是否相等,如果都相等,则为对称数,跳出循环。 - 计算车速,为
(n-n2)/2,即新里程与初始里程的差值除以2。 - 输出车速和新的对称数里程
n。
1261. 韩信点兵
问题描述
韩信有一队士兵,他想知道有多少人,他就让士兵报数,如果按照 1 到 5 报数,最末一个士兵报的数为 1 。
按照 1到 6 报数,最末一个士兵报的数为 5 。
按照 1 到 7 报数,最末一个士兵报的数为 4 。
最后再按 1 到11 报数,最末一个士兵报的数为 10 。
请问韩信这队士兵最少有多少人?
解题思路
我们可以从1开始依次递增,对每个数分别模5、6、7、11,判断是否满足题目要求的条件。
- 初始化变量
num为1,表示当前检查的数。 - 使用while循环,条件为
true,即无限循环。 - 在循环内,判断
num是否满足以下条件:num模5的余数为1。num模6的余数为5。num模7的余数为4。num模11的余数为10。
- 如果
num满足所有条件,跳出循环。 - 如果
num不满足条件,将num加1,继续下一轮循环。 - 输出满足条件的
num值。
代码实现
#include <iostream>
using namespace std;
int main() {int num = 1; // 初始化num为1while (true) { // 无限循环if (num % 5 == 1 && num % 6 == 5 && num % 7 == 4 && num % 11 == 10) {break; // 如果num满足所有条件,跳出循环}num++; // 如果num不满足条件,num加1,继续下一轮循环}cout << num << endl; // 输出满足条件的num值return 0;
}
代码解析
- 初始化变量
num为1,表示当前检查的数。 - 使用while循环,条件为
true,即无限循环。 - 在循环内,判断
num是否满足以下条件:num % 5 == 1:num模5的余数为1。num % 6 == 5:num模6的余数为5。num % 7 == 4:num模7的余数为4。num % 11 == 10:num模11的余数为10。
- 如果
num满足所有条件,使用break语句跳出循环。 - 如果
num不满足条件,将num加1,继续下一轮循环。 - 输出满足条件的
num值。
相关文章:

6、while循环 - 习题解析
目录 解析部分:分支练习1244. 请问一个正整数能够整除几次2问题描述解题思路代码实现代码解析 1062. 求落地次数问题描述解题思路代码实现代码解析 1254. 求车速问题描述解题思路代码实现代码解析 1261. 韩信点兵问题描述解题思路代码实现代码解析 解析部分…...

ReentrantLock可重入锁
可重⼊锁,这个锁可以被线程多次重复进⼊进⾏获取操作。 ReentantLock继承接⼝Lock并实现了接⼝中定义的⽅法,除了能完成synchronized所能完成的所有⼯作 外,还提供了诸如可响应中断锁、可轮询锁请求、定时锁等避免多线程死锁的⽅法。 在并发量…...

如何秒杀系统架构设计
原文路径:https://learn.lianglianglee.com/%e4%b8%93%e6%a0%8f/%e5%a6%82%e4%bd%95%e8%ae%be%e8%ae%a1%e4%b8%80%e4%b8%aa%e7%a7%92%e6%9d%80%e7%b3%bb%e7%bb%9f/00%20%e5%bc%80%e7%af%87%e8%af%8d%20%e7%a7%92%e6%9d%80%e7%b3%bb%e7%bb%9f%e6%9e%b6%e6%9e%84%e8%ae%be%e8%ae%…...
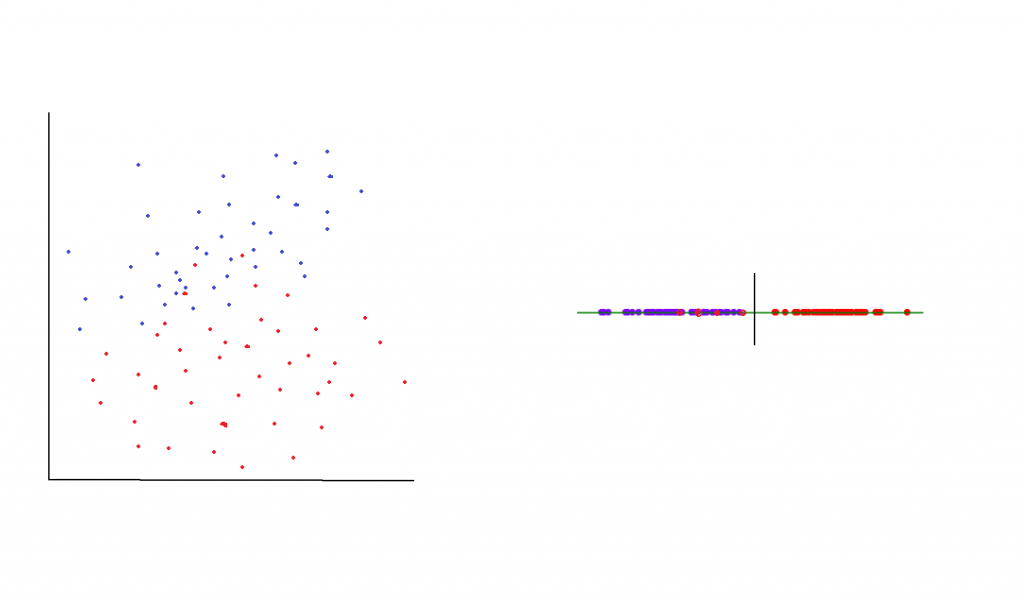
深度神经网络——什么是降维?
引言 什么是降维? 降维是用于降低数据集维度的过程,采用许多特征并将它们表示为更少的特征。 例如,降维可用于将二十个特征的数据集减少到仅有几个特征。 降维通常用于无监督学习任务 降维是一个用于降低数据集维度的过程,采用许…...

SpringMVC—RequestMapping注解
一、RequestMapping注解 RequestMapping注解:是Spring MVC框架中的一个控制器映射注解,用于将请求映射到相应的处理方法上,具体来说,他可以将指定URL的请求绑定到一个特定的方法或类上,从而实现对请求的处理和响应。 …...

Java线程池基本概念
全局和局部线程池 全局线程池 在Spring框架中,全局线程池如ThreadPoolTaskExecutor通常是作为Spring Bean存在的,它们的生命周期由Spring容器管理。当Spring容器关闭时,这些线程池也会被适当地清理和关闭。因此,开发者通常不需要手…...

智能车联网安全发展形势、挑战
一、技术演进加速车联网安全环境复杂变化 当前,5G、大数据、大算力、大模型等技术正加速在车联网领域实现融合应用。车联网的网络通信能力、感知计算水平以及创新业务应用都在快速发展,与此同时,车联网的网络安全环境也在随之演进变化&#…...

AWS概述
AWS概述EMR Serverless Aamzon Web Services提供了一系列全球范围的云产品,包括计算、存储、数据库、分析、网络、移动、开发工具、管理工具、IoT、安全和企业应用:按需交付、及时可用、采用随用随付的定价模式。你可以畅享200多种服务,从数据…...
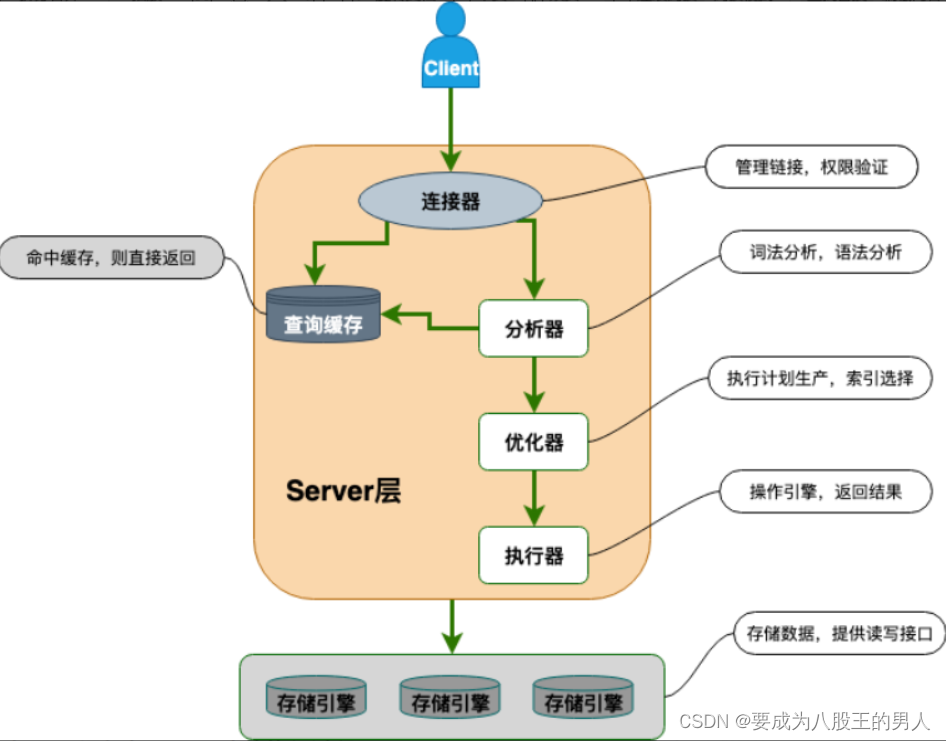
MySQL常见面试题自测
文章目录 MySQL基础架构一、说说 MySQL 的架构?二、一条 SQL语句在MySQL中的执行过程 MySQL存储引擎一、MySQL 提供了哪些存储引擎?二、MySQL 存储引擎架构了解吗?三、MyISAM 和 InnoDB 的区别? MySQL 事务一、何谓事务࿱…...

c语言回顾-函数递归
1.递归的介绍 1.1什么是递归 递归是指在一个函数的定义中调用自身的过程。简单来说,递归是一种通过重复调用自身来解决问题的方法。 递归包括两个关键要素:基本情况和递归情况。基本情况是指当问题达到某个特定条件时,不再需要递归调用&am…...
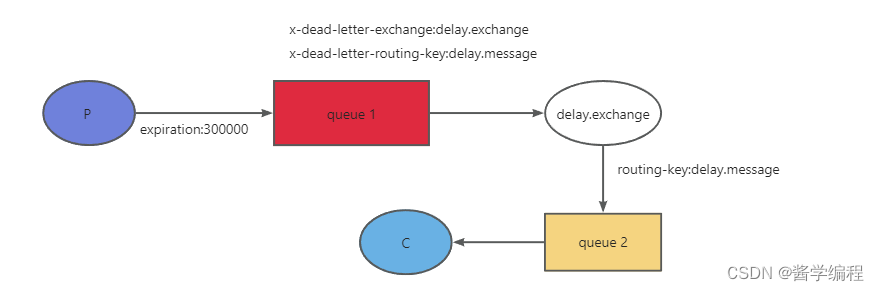
消息队列-RabbitMQ-延时队列实现
死信队列 DLX,全称为Dead-Letter-Exchange,死信交换机,死信邮箱。当消息在一个队列中变成死信之后,它能重新发送到另外一个交换器中,这个交换器就是DLX,绑定DLX的队列就称为死信队列。 导致死信的几种原因: ● 消息…...

【热门开源项目推荐】满足不同程序员的需求与关注点
目录 前言一、热门开源项目介绍二、使用开源热门项目的优势(一)经济方面(二)技术方面(三)社区支持及协作方面 三、程序员选择项目模型建议(一)关键步骤(二)示…...
)
一文理清GO语言日志库实现开发项目中的日志功能(rotatelogs/zap分析)
一文理清GO语言日志库实现开发项目中的日志功能(rotatelogs/zap分析) rotatelogs rotatelogs 是一个用于管理日志文件的 Go 语言库,它提供了自动轮换、压缩和删除旧日志文件的功能。这个库可以帮助你更好地管理和维护你的应用程序日志。要使…...
【Go语言精进之路】构建高效Go程序:了解string实现原理并高效使用
🔥 个人主页:空白诗 🔥 热门专栏:【Go语言精进之路】 文章目录 引言一、Go语言的字符串类型1.1 字符串的定义1.2 字符串的零值可用1.3 字符串的不可变性1.4 字符串的拼接1.5 字符串的常用方法1.6 实际使用示例 二、字符串的内部表…...

HDFS 常见命令
在HDFS创建文件夹:hdfs dfs -mkdir /test 复制本地文件到HDFS中某个目录下:hdfs dfs -put /本地路径 /hdfs 路径 查看文件内容:hdfs dfs -cat /test.txt 查看当前文件夹目录:hdfs dfs -ls / 查看文件夹中的文件数:…...

示例:WPF中应用Grid的SharedSizeGroup设置整齐的布局
一、目的:应用Grid的SharedSizeGroup设置整齐的布局 二、实现 <ItemsControl ItemsSource"{local:GetStudents Count5}"><ItemsControl.ItemTemplate><DataTemplate><Grid ShowGridLines"True"><Grid.ColumnDefinit…...

React的form表单自定义校验规则
使用antd开发的过程中,必定会遇到需要对form表单进行必填校验的处理,正常情况下,我们都会一个空的必填校验,如下:一般我们只需要简单配置rules即可 <FormItem label"管理员姓名" {...itemLayout.wholeLi…...
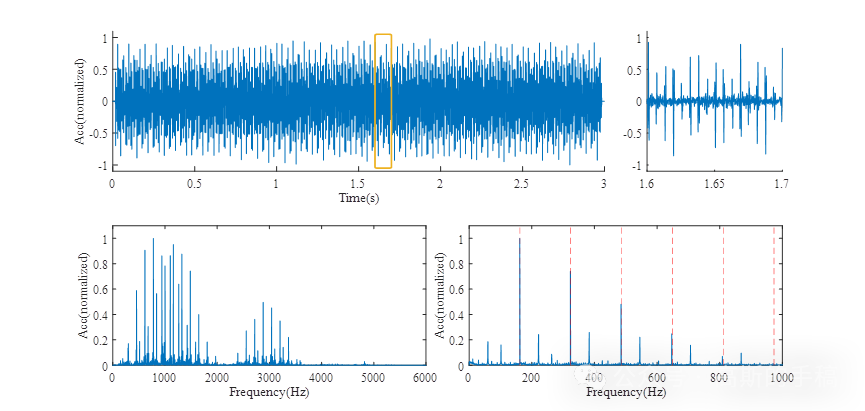
一种新的一维时间序列信号盲解卷积算法(以旋转机械故障诊断为例,MATLAB环境)
一种新的一维时间序列信号盲解卷积算法(以旋转机械故障诊断为例,MATLAB环境),可作为深度学习信号前处理过程,水个SCI不是问题。 机械设备的状态信号中往往蕴含着大量的设备异常信息。如何从繁多的机械状态信号中提取足…...
618电商是社区网站入局的好时机吗?
近日,随着618大促的临近,许多内容平台像B站、小红书等纷纷被电商活动所充斥,让用户感觉仿佛被电商绑架一般。这种用户体验的极度不佳让人开始思考,难道这就是互联网社区的未来发展方向吗? 在所有平台性质的社区中&…...

不知道密码,一样能卸载瑞星esm防病毒终端安全防护系统
离开单位后试图卸载瑞星的时候却发现还需要密码,真是烦死了。研究了几分钟后找到了完美卸载方法。 首先,让我们请出老流氓360安全卫士,下载好它,让右键菜单出现使用 360强力删除这一选项。 之后,进入安全模式&#x…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
