【BFS算法】广度搜索·由起点开始逐层向周围扩散求得最短路径(算法框架+题目)
0、前言
深度优先搜索是DFS(Depth Frst Search),其实就是前面所讲过的回溯算法,它的特点和它的名字一样,首先在一条路径上不断往下(深度)遍历,获得答案之后再返回,再继续往下遍历。这也是递归的思想,所以这也是为什么回溯算法通常都是用递归来写,而下面的BFS由于不是这种思路从而没有用递归。
广度优先算法(Breath First Search)其实和深度优先算法是一对兄弟,因为它们的解空间都是树形解空间,并且都是在求解过程中 动态生成树形解空间。广度优先算法在于,它在动态生成解空间从而获得答案时,是从一层一层(广度的)取构建并搜索答案。
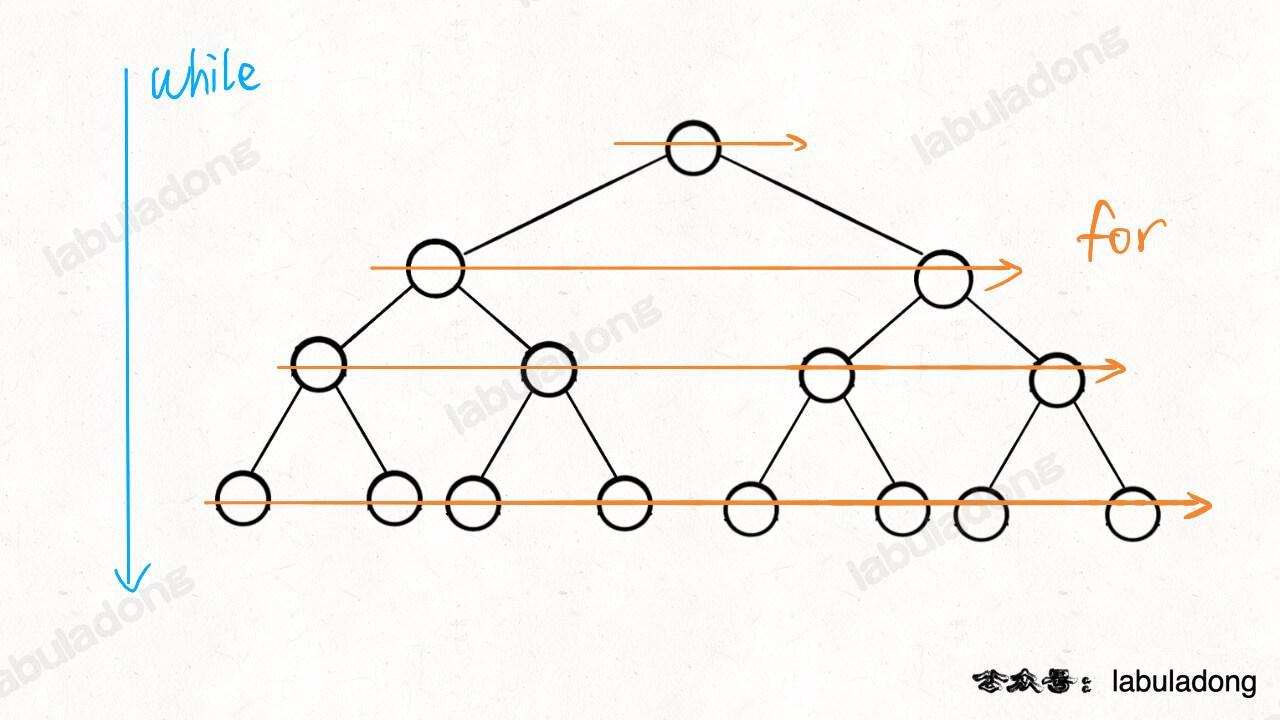
它的核心思想是:把问题的求解抽象为一个图,从一个起点开始,向四周去扩散,不断扩散直至求得答案。
BFS和DFS的主要区别在于:
- 在查找路径问题上,BFS查找出来的路径是最短的
- BFS的空间复杂度要比DFS高(这也是BFS的代价)
一、算法框架
知道它的核心思想之后,其实我们就可以写出它的算法框架,本质就是遍历图:
//计算起点start到终点target的最短距离
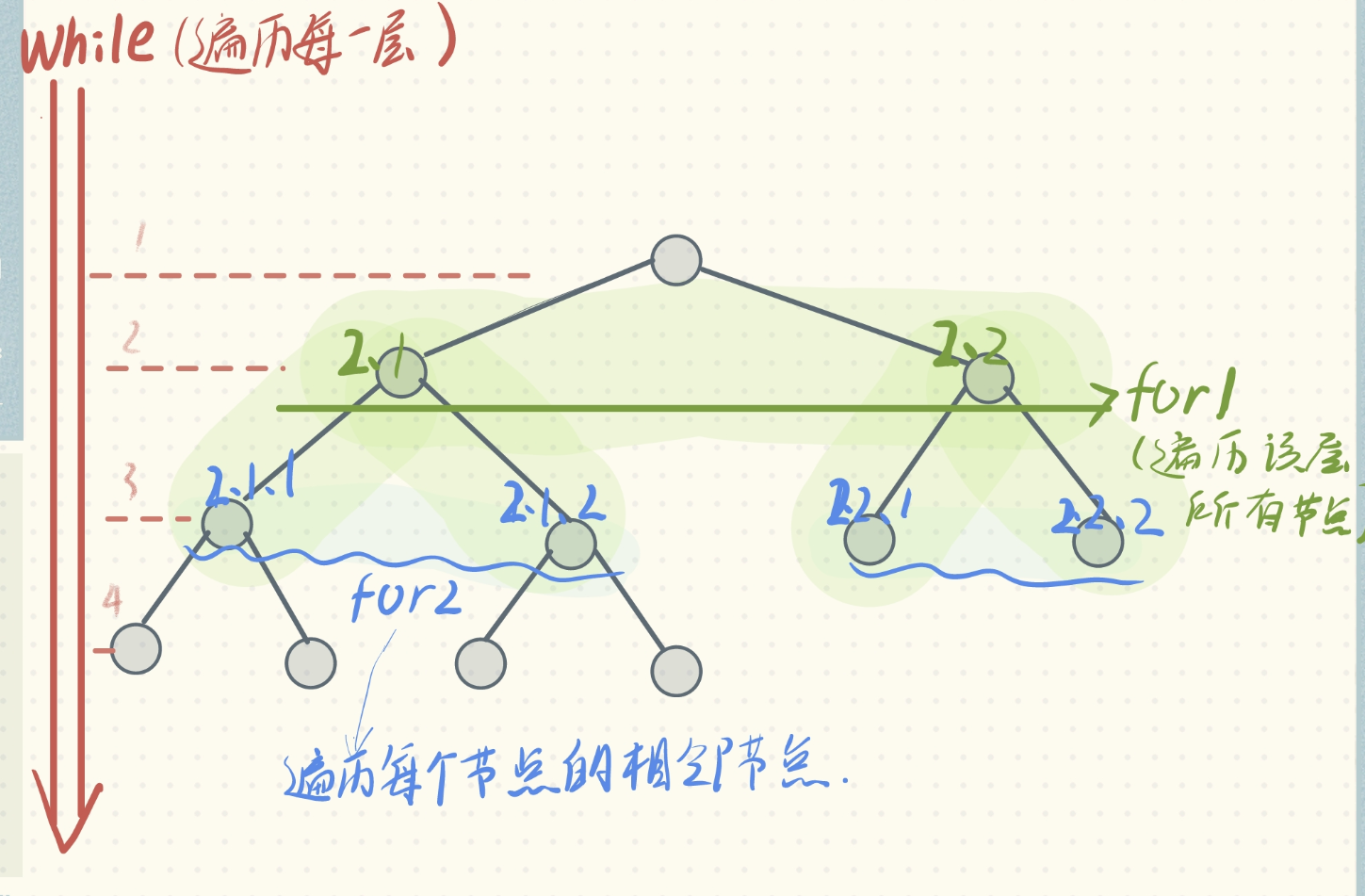
int BFS(Node start, Node target) {queue<Node> q; //核心数据结构set<Node> visited; //避免走回头路q.push(start); //将起点加入队列visited.insert(start);//走完一次完整的下面1,2,3循环,代表以当前层节点完整的依次向外扩散了一层//循环1:从起点开始,不断将当前队列中所有节点向四周扩散while (!q.empty()) {int sz = q.size();//2:循环2:队列中所有节点依次往外扩散一层for (int i = 0; i < sz; i++) {Node cur = q.front();q.pop();if (cur == target)return step;//循环3:把当前层的队列节点往外扩散一层,并把扩散得到的加入队列for (Node x : cur.adj()) {if (visited.count(x) == 0) {q.push(x);visited.insert(x);}}}}// 如果走到这里,说明在图中没有找到目标节点
}- 其中
Queue<Node> q是队列,存储当前遍历层和即将遍历层的节点,是BFS的核心数据结构; cur.adj()泛指与当前遍历到的这个节点cur相邻的节点(也就是与cur相连的下一层的节点,不如二维数组中cur上下左右四个位置就是相邻节点);visited的作用防止走回头路;(但是对于二叉树这种结构,没有子节点到父节点的指针,不会走回头路也就不需要visited)
二、题目
2.1:二叉树的最小高度
1.题目
🔗111. 二叉树的最小深度
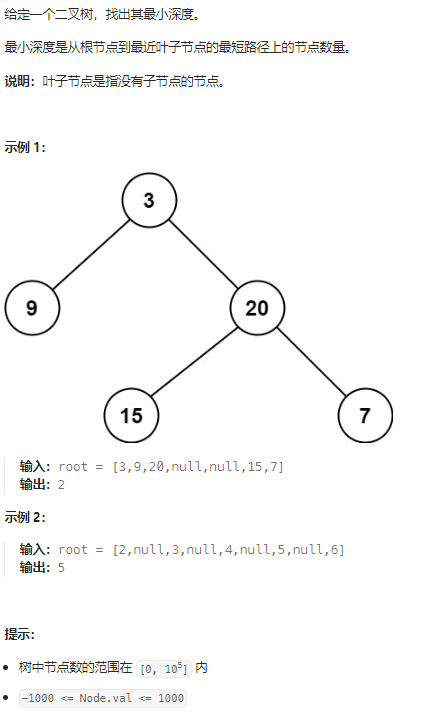
2.思路
这道题就是非常典型和简单的BFS算法,我们只需要把上面算法框架中的cur == target找到目标答案的位置改成找到叶子节点:cur.left == null && cur.right == null即可
3.代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {if(root == nullptr) return 0;queue<TreeNode*> q; //核心数据结构,用来存储当前节点int depth = 0; //记录当前层的深度//将第一层输入队列:即起点q.push(root);//从当前层逐层扩散和遍历:循环1:遍历层while(!q.empty()){//获取当前层所以节点数量int sz = q.size();depth++;//循环2:遍历当前层的所有节点for(int i = 0; i < sz; i++){TreeNode* cur = q.front();q.pop();//判断当前遍历到的这个节点释放符合答案需求if(cur->left == nullptr && cur->right == nullptr)return depth;//循环3:以当前层的当前节点往外再扩一层,并把扩散得到的下一层节点加入队列//这里就已经确定了是左右孩子两个相邻节点,就不写循环了if(cur->left!=nullptr) q.push(cur->left);if(cur->right!=nullptr) q.push(cur->right);}}return 0;}
};
2.2:解开密码锁的最少次数
1.题目
🔗752. 打开转盘锁

2.思路
- 分析:题目要求我们从
0000开始,根据旋转规则,每次只能向上或向下旋转一次四个数位的其中一位,通过不断的旋转直到四位数字为最终答案target。 - 关键:把问题抽象成一张图,当前4位数字密码为节点,通过当前密码状态选择一个数位向上或向下旋转一次得到下一个四位数(节点),每个节点可以实现
2x2x2x2 = 8种选择得到下一个节点;即:该问题抽象为一张图,每个节点有8个相邻节点,我们需要从起始节点"0000"以最短路径寻找到我们的目标节点target(注意还有限制条件)
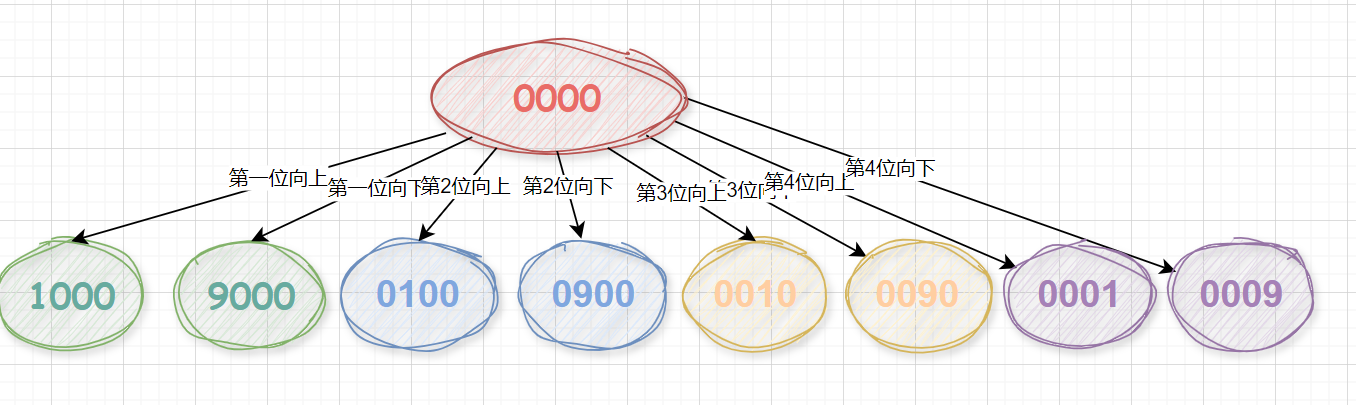
有了上述分析后,大概有对这个题有了一个这个题的把握和认识,但是其实还有很多细节没有分析到。当然,一下子其实分析不到所有的细节是很正常,我们一步一步来,慢慢完善。
- 首先,我们先不考虑【死亡密码】的限制,想一想,从
"0000"出发,穷举出所有密码的可能,我们需要怎么做;也就是说,从"0000"出发,每个节点有8个相邻,我们以BFS遍历出所有密码
//BFS框架,打印出所有可能的密码
void BFS(string target){queue<string> q;q.push("0000");while(!q.empty()){int sz = q.size();//将当前层(也就是当前队列)中节点向下一层(周围)扩散for(int i = 0; i < sz; i++){//获取当前节点string cur = q.front(); q.pop();//判断是否达到终点cout << cur << endl;//将当前节点相邻的周围节点(也就是下一层的)加入到队列for(int j = 0; j < 4; j++){//当前位向上拨string up = plusOne(cur, j);q.push(up);//当前位向下拨string down = minusOne(cur, j);q.push(down);}}//在这里增加步数}
}
上面代码中的plusOne和minusOne函数的代码如下:
string plusOne(string s, int j) {if (s[j] == '9') s[j] = '0';else s[j] += 1;return s;
}string minusOne(string s, int j) {if (s[j] == '0') s[j] = '9';else s[j] -= 1;return s;
}
- 当然,上述代码还有很多问题
- 首先,会走回头路,比如从
"0000"到"1000"但是"1000"的8个相邻点里面又有"0000"这样下去会产生死循环。这个时候就需要额外加一个集合数据结构visited,记录下来已经走过的节点,在往下扩散的时候(也就是往队列里面加元素的时候)进行判断,是否已经遍历过。 - 没有终止条件,这个其实挺好改的,只需要在遍历到那个具体的节点的时候加一个判断条件,遇到
target结束循环并返回即可。 - 没有对限制条件(不能出现死亡密码)的处理
3.代码
class Solution {
public:string plusOne(string s, int j) {if (s[j] == '9') s[j] = '0';else s[j] += 1;return s;
}string minusOne(string s, int j) {if (s[j] == '0') s[j] = '9';else s[j] -= 1;return s;
}int openLock(vector<string>& deadends, string target) {unordered_set<string> deads; //记录限制条件:需要跳过的死亡密码for(string s : deadends){deads.insert(s);}//记录已经穷举过的密码,防止走回头路unordered_set<string> visited;queue<string> q;int step = 0;//从起点开始进行BFSq.push("0000");visited.insert("0000");while(!q.empty()){int sz = q.size();for(int i = 0; i < sz; i++){string cur = q.front();q.pop();if(deads.count(cur)) continue; //分支限界,在遍历到这个节点的时候限制就行//判断是否达到终止条件if(cur == target) return step;for(int j = 0; j < 4; j++){string left = plusOne(cur,j);if(!visited.count(left) ){q.push(left);visited.insert(left);}string right = minusOne(cur,j);if(!visited.count(right)) {q.push(right);visited.insert(right);}}}step++;}return -1;}
};
2.3:布线问题
1.题目
印刷电路板将布线区域划分成n*m个方格阵列,精确的电路布线问题要求确定连接方格a的中点到方格b的中点的最短布线问题。在布线时,电路只能沿着直线或直角布线。为了避免线路相交,已布了线的方格做了封锁标记,其他线路不允许穿过被封锁的方格。
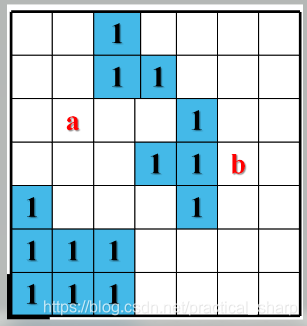
2.思路
- 分析:其实这个题就是有障碍物的迷宫问题。本质上也是抽象为图问题,格子上每一个点的坐标位置就是一个节点,一个节点可以往上下左右4个方向行走到达其他位置(节点);注意限制条件:不能在障碍物(也就是题目所说的封锁方格)处进行遍历,所以遇到该限制条件就跳过且不扩展该样的节点。
- 关键:
- 用一个队列来进行BFS搜索,找到起点位置到终点位置的最短路径
- 用一个二维布尔数组
visited来存储对应位置处方格是否被访问过(避免走回头路) - 用一个二维数组来记录封锁方格(其实就是存储初始棋盘
grid[][]) - 如果需要记录最终得到的那个最短路径,可以设置一个以
pair<int, int>为元素的二维数组,记录(x,y)位置是由parent[x][y]得来的(记录路径,能从目标节点反推回去完整路径)
3.代码
#include <iostream>
#include <vector>
#include <queue>
#include <tuple>using namespace std;//定义节点可以扩展的四个方向:上下左右{x,y}
vector< pair<int, int> > dirs ={{-1,0}, {1,0}, {0,-1}, {0, 1}};/*辅助函数,判断该节点是否合法1. 不能超过整个迷宫(电线板)边界2. 不能被访问过(不能走回头路)3. 不能是封锁节点(即迷宫里的障碍物
*/
bool isValid(int x, int y, int n, int m, vector<vector<int>>& grid, vector <vector<bool>>& visited){return x >= 0 && x <n && y>=0 && y < m && grid[x][y] != -1 && !visited[x][y];
}//BFS算法求解最短路径并标记路径节点
vector <vector<int>> shortestPath(vector<vector<int>>& grid, pair<int, int> Start, pair<int, int> End){int n = grid.size();int m = grid[0].size();//队列,存储当前坐标和部署queue<tuple<int, int, int>> q;//已经访问节点的存储vector<vector<bool>> visited(n, vector<bool>(m, false));//记录当前节点是由哪个节点得来(记录路径)vector<vector<pair<int, int>>> parent(n, vector<pair<int, int>>(m, make_pair(-1, -1)));//将起点加入队列q.push(make_tuple(Start.first, Start.second, 0));visited[Start.first][Start.second] = true;bool found = false; //标记是否找到,一旦找到,路径最短, 退出while(!q.empty()){int sz = q.size();//遍历该层for(int i = 0; i < sz; i++){//先拿出当前节点auto [cur_x, cur_y, steps] = q.front();q.pop();//可选:判断当前节点是否合理(其实没必要,起点肯定一般都是合理,保证在下面扩展的时候不添加不合理的即可//判断是否达到终点if( cur_x == End.first && cur_y == End.second){found = true;break;}//扩展四个方向for(auto [dx, dy] : dirs){int newX = cur_x + dx;int newY = cur_y + dy;//判断合法if(isValid(newX, newY, n, m, grid, visited)){q.push(make_tuple(newX, newY, steps+1));visited[newX][newY] = true;//记录父节点parent[newX][newY] = make_pair(cur_x, cur_y);}}}}if(found){int x = End.first;int y = End.second;while(!(x == Start.first && y == Start.second)){grid[x][y] = 1;tie(x,y) = parent[x][y];}grid[Start.first][Start.second] = 1; //标记起点}return grid;
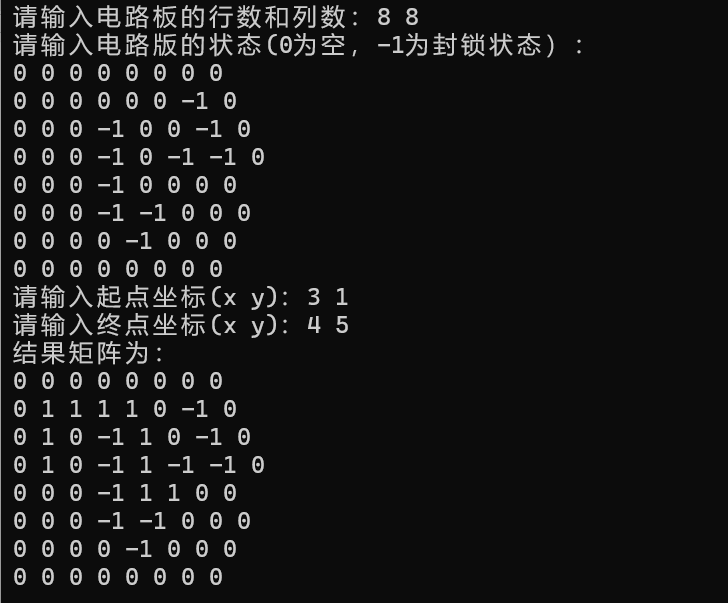
}int main(){//输入int n, m;cout << "请输入电路板的行数和列数:";cin >> n >> m;vector <vector<int>> grid (n, vector<int>(m, 0));cout << "请输入电路版的状态(0为空,-1为封锁状态):"<<endl;for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){cin >> grid[i][j];}}int startX, startY, endX, endY;cout << "请输入起点坐标(x y):";cin >> startX >> startY;cout << "请输入终点坐标(x y):";cin >> endX >> endY;//BFS遍历vector< vector<int> > res = shortestPath(grid, {startX, startY}, {endX, endY});//输出结果cout << "结果矩阵为:"<< endl;for(const auto& row : res){for(int cell : row){cout << cell << " ";}cout << endl;}return 0;
}
end:本文参考
🔗labuladongBFS算法解题套路框架
🔗布线问题分支界限法求解
相关文章:

【BFS算法】广度搜索·由起点开始逐层向周围扩散求得最短路径(算法框架+题目)
0、前言 深度优先搜索是DFS(Depth Frst Search),其实就是前面所讲过的回溯算法,它的特点和它的名字一样,首先在一条路径上不断往下(深度)遍历,获得答案之后再返回,再继续往下遍历。…...

微信小程序---登录
手机号登录 手机号快速验证和手机号实时验证区别 手机号快速验证组件,平台会对号码进行验证,但不保证是实时验证;收费0.0.3元手机号实时验证组件,在每次请求时,平台均会对用户选择的手机号进行实时验证。收费0.0.4元…...

IPython大师课:提升数据科学工作效率的终极工具
IPython是一个增强的Python交互式shell,它提供了丰富的功能和易用性改进,特别适合进行数据分析、科学计算和一般的Python开发。本文将全面介绍IPython的基本概念、使用方法、主要作用以及注意事项。 一、IPython简介 1. IPython的起源 IPython最初由Fe…...
抖音素材网站平台有哪些?素材下载网站库分享
在这个视觉信息充斥的时代,抖音已经成为众多自媒体人展示才华的舞台。要在众多创作者中脱颖而出,不仅需要独特的创意,还需要优质的素材来支持你的内容制作。今天,我将介绍几个为抖音视频提供高品质素材的网站,包括国内…...

MODBUS TCP协议实例数据帧详细分析
MODBUS TCP协议实例数据帧详细分析 1.简介 2.ModbusTCP数据帧 2.1.报文头MBAP 2.2.帧结构PDU 3.ADU详细结构 3.1. 0x01:读线圈 3.2. 0x02:读离散量输入 3.3. 0x03:读保持寄存器 3.4. 0x04:读输入寄存器 3.5. 0x05:写单…...

Spring Boot启动与运行机制详解:初学者友好版
Spring Boot启动与运行机制详解:初学者友好版 随着微服务的兴起和容器化部署的流行,Spring Boot以其快速搭建、简单配置和自动化部署的特性,成为了众多开发者的首选。对于初学者而言,理解Spring Boot的启动与运行机制是掌握其精髓…...
Ubuntu 22.04 解决 firefox 中文界面乱码
问题复现 在为Ubuntu 22.04 Server安装完整的GNOME 42.01桌面后,将桌面语言设置为中文时,打开Firefox可能会出现中文乱码的问题。经过网上调查发现,这个问题是由Snap软件包引起的。 解决方案 为了避免在Ubuntu 22.04中文模式下的乱码问题…...

前端面试题日常练-day77 【面试题】
题目 希望这些选择题能够帮助您进行前端面试的准备,答案在文末 在Sass中,以下哪个功能用于将样式规则应用于多个选择器? a) extend b) mixin c) import d) include Sass中的嵌套规则(Nested Rules)有助于实现以下哪个…...
团队协同渗透测试报告输入输出平台部署
目录 简介 文章来源 部署环境 文件下载 开始安装 系统初始化 免责声明 结语 简介 因应监管部需求,国内访问Docker源pull镜像开始变得复杂且困难起来了,大佬github给的在线/离线安装脚本跑了很久也无法拉取到镜像,所以将以前的镜像打…...

vue3-父子通信
一个简单的vue3子组件调用父组件方法的demo <template> <div> <h2>Parent Component父组件</h2> <ChildComponent notify-parent"handleParentMethod" /> </div> </template> <script> import { ref } fr…...

微信小程序—页面滑动,获取可视区域数据
需求:页面有一列表,获取可视区域的数据;滑动过程中不处理,停止滑动后才获取。 实现原理:获取列表中每个条目的位置信息(元素顶部距可视区域顶部的距离),和可视区域比较,…...
—委托)
C#语言进阶(一)—委托
总目录 C# 语法总目录 委托 委托1. 基本用法2.委托作为方法参数3.多播委托4.实例对象方法、静态方法与委托之间的关系5. 委托类型参数为泛型6. System空间下的 Func 委托和 Action 委托 委托 委托类似于CPP中的函数指针。它定义了一个方法类型,这个方法类型有返回类…...
VST3音频插件技术介绍
一.概述 1.VST3介绍 VST3(Virtual Studio Technology 3)是一种音频插件格式,由Steinberg公司开发,用于在数字音频工作站(DAW)中使用。VST3插件可以是模拟合成器、鼓机、混响器、压缩器等多种类型的音频处理…...

MySQL数据库管理 二
1、数据表高级操作 (1)克隆表 方法一: create table 新表名 like 旧表名; #克隆表结构 insert into 新表名 select * from 旧表名; #克隆表数据 #此方法能保证 新表的表结构、表数据 跟旧表都是一致的 方法二&#x…...

android system UI 基础的基础
Android 系统中的 SystemUI 是一种特殊的应用程序,它负责管理和显示设备的用户界面组件,例如状态栏、导航栏和最近任务列表等。SystemUI 是在 Android 启动过程中由 Zygote 进程启动的。以下是 SystemUI 启动过程的详细步骤: SystemUI 启动过…...

ARM32开发——GD32F4定时器查询
🎬 秋野酱:《个人主页》 🔥 个人专栏:《Java专栏》《Python专栏》 ⛺️心若有所向往,何惧道阻且长 文章目录...
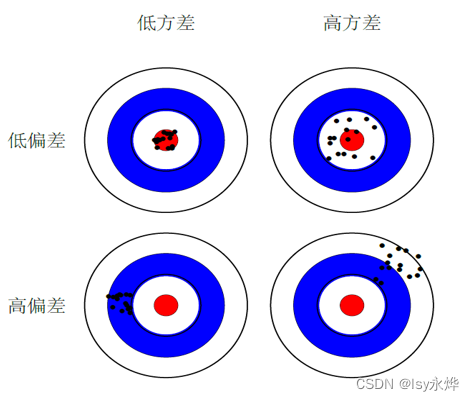
【机器学习】第7章 集成学习(小重点,混之前章节出题但小题)
一、概念 1.集成学习,顾名思义,不是一个玩意,而是一堆玩意混合到一块。 (1)基本思想是先 生成一定数量基学习器,再采用集成策略 将这堆基学习器的预测结果组合起来,从而形成最终结论。 &#x…...

代码随想录——子集Ⅱ(Leecode 90)
题目链接 回溯 class Solution {List<List<Integer>> res new ArrayList<List<Integer>>();List<Integer> list new ArrayList<Integer>();boolean[] used; public List<List<Integer>> subsetsWithDup(int[] nums) {use…...
)
vue关闭页面时触发的函数(ai生成)
在Vue中,可以通过监听浏览器的beforeunload事件来在关闭页面前触发函数。这里是一个简单的示例: new Vue({el: #app,methods: {handleBeforeUnload(event) {// 设置returnValue属性以显示确认对话框event.returnValue 你确定要离开吗?;// 在…...

马尔可夫性质与Q学习在强化学习中的结合
马尔可夫性质是强化学习(RL)算法的基础,特别是在Q学习中。马尔可夫性质指出,系统的未来状态只依赖于当前状态,而与之前的状态序列无关。这一性质简化了学习最优策略的问题,因为它减少了状态转移的复杂性。 …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
