马尔可夫性质与Q学习在强化学习中的结合
马尔可夫性质是强化学习(RL)算法的基础,特别是在Q学习中。马尔可夫性质指出,系统的未来状态只依赖于当前状态,而与之前的状态序列无关。这一性质简化了学习最优策略的问题,因为它减少了状态转移的复杂性。
马尔可夫性质
形式上,对于一个过程 {Xt}\{X_t\}{Xt},如果在任意时间 ttt 和状态 x0,x1,…,xt,xt+1x_0, x_1, \ldots, x_t, x_{t+1}x0,x1,…,xt,xt+1 下,以下等式成立,则该过程具有马尔可夫性质:
P(Xt+1=xt+1∣Xt=xt,Xt−1=xt−1,…,X0=x0)=P(Xt+1=xt+1∣Xt=xt)P(X_{t+1} = x_{t+1} | X_t = x_t, X_{t-1} = x_{t-1}, \ldots, X_0 = x_0) = P(X_{t+1} = x_{t+1} | X_t = x_t)P(Xt+1=xt+1∣Xt=xt,Xt−1=xt−1,…,X0=x0)=P(Xt+1=xt+1∣Xt=xt)
这意味着给定当前状态,过程的未来演变与过去的历史状态无关。
Q学习中的马尔可夫性质
Q学习是一种无模型强化学习算法,旨在通过估计状态-动作对的价值(即Q值)来学习最优策略。马尔可夫性质对于Q学习至关重要,因为它确保了Q值可以根据当前状态和动作进行迭代更新,而无需考虑整个历史状态和动作序列。
Q学习算法使用以下公式更新给定状态-动作对的Q值:
Q(s,a)←Q(s,a)+α(r+γmaxa′Q(s′,a′)−Q(s,a))Q(s, a) \leftarrow Q(s, a) + \alpha \left( r + \gamma \max_{a'} Q(s', a') - Q(s, a) \right)Q(s,a)←Q(s,a)+α(r+γmaxa′Q(s′,a′)−Q(s,a))
其中:
- sss 是当前状态,
- aaa 是执行的动作,
- rrr 是收到的奖励,
- s′s's′ 是下一个状态,
- α\alphaα 是学习率,
- γ\gammaγ 是折扣因子,
- maxa′Q(s′,a′)\max_{a'} Q(s', a')maxa′Q(s′,a′) 是下一个状态 s′s's′ 的最大估计未来奖励。
马尔可夫性质在Q学习中的作用
-
状态-动作独立性:给定当前状态 sss 和动作 aaa,下一个状态 s′s's′ 和奖励 rrr 独立于之前的状态和动作。这简化了Q学习的更新规则,因为它只需要当前状态和动作来更新Q值。
-
转移概率:转移概率 P(s′∣s,a)P(s'|s, a)P(s′∣s,a) 仅依赖于当前状态和动作,而与之前的状态无关。这使得状态转移和奖励的计算更为简便,从而提高了学习效率。
相关文章:

马尔可夫性质与Q学习在强化学习中的结合
马尔可夫性质是强化学习(RL)算法的基础,特别是在Q学习中。马尔可夫性质指出,系统的未来状态只依赖于当前状态,而与之前的状态序列无关。这一性质简化了学习最优策略的问题,因为它减少了状态转移的复杂性。 …...

【LeetCode 5.】 最长回文子串
一道题能否使用动态规划就在于判断最优结构是否是通过最优子结构推导得到?如果显然具备这个特性,那么就应该朝动态规划思考。如果令dp[i][j]表示串s[i:j1]是否是回文子串,那么判断dp[i][j] 是否是回文子串,相当于判断s[i] 与 s[j]…...

联邦学习周记|第四周
论文:Active Federated Learning 链接 将主动学习引入FL,每次随机抽几个Client拿来train,把置信值低的Client概率调大,就能少跑几次。 论文:Active learning based federated learning for waste and natural disast…...
机器学习课程复习——逻辑回归
1. 激活函数 Q:激活函数有哪些? SigmoidS型函数Tanh 双曲正切函数...
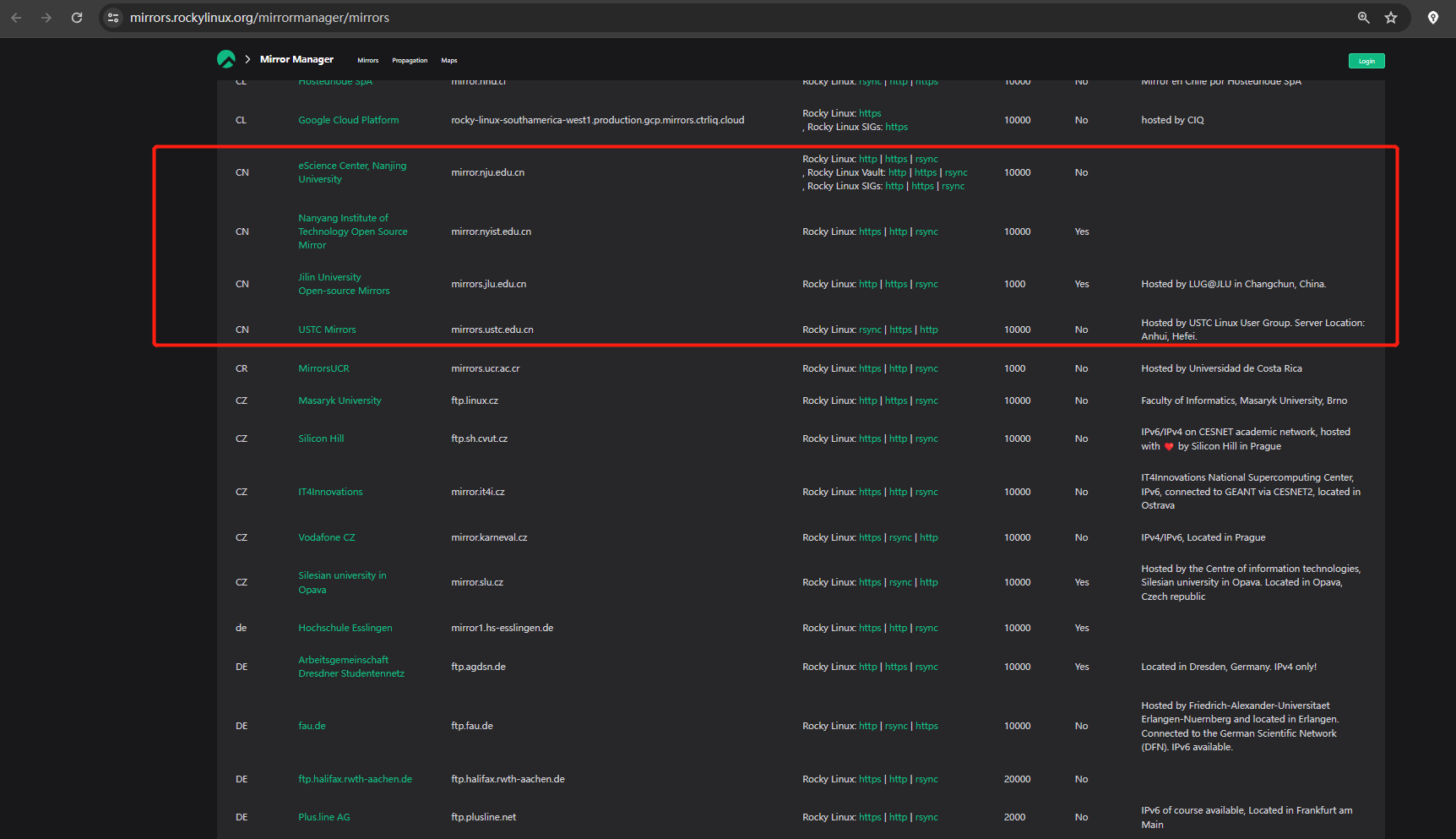
Rocky Linux 更换CN镜像地址
官方镜像列表,下拉查找 官方镜像列表:https://mirrors.rockylinux.org/mirrormanager/mirrorsCN 开头的站点。 一键更改镜像地址脚本 以下是更改从默认更改到阿里云地址 cat <<EOF>>/RackyLinux_Update_repo.sh #!/bin/bash # -*- codin…...

Linux rm命令由于要删的文件太多报-bash: /usr/bin/rm:参数列表过长,无法删除的解决办法
银河麒麟系统,在使用rm命令删除文件时报了如下错误,删不掉: 查了一下,原因就是要删除的文件太多了,例如我当前要删的文件共有这么多: 查到了解决办法,记录在此。需要使用xargs命令来解决参数列表…...
【包管理】Node.JS与Ptyhon安装
文章目录 Node.JSPtyhon Node.JS Node.js的安装通常包括以下几个步骤: 访问Node.js官网: 打开Node.js的官方网站(如:https://nodejs.org/zh-cn/download/)。 下载安装包: 根据你的操作系统选择对应的Node…...

SpringMVC系列四: Rest-优雅的url请求风格
Rest请求 💞Rest基本介绍💞Rest风格的url-完成增删改查需求说明代码实现HiddenHttpMethodFilter机制注意事项和细节 💞课后作业 上一讲, 我们学习的是SpringMVC系列三: Postman(接口测试工具) 现在打开springmvc项目 💞Rest基本介…...

Hexo 搭建个人博客(ubuntu20.04)
1 安装 Nodejs 和 npm 首先登录NodeSource官网: Nodesource Node.js DEB 按照提示安装最新的 Node.js 及其配套版本的 npm。 (1)以 sudo 用户身份运行下面的命令,下载并执行 NodeSource 安装脚本: sudo curl -fsSL…...

【论文阅读】-- Attribute-Aware RBFs:使用 RT Core 范围查询交互式可视化时间序列颗粒体积
Attribute-Aware RBFs: Interactive Visualization of Time Series Particle Volumes Using RT Core Range Queries 摘要1 引言2 相关工作2.1 粒子体渲染2.2 RT核心方法 3 渲染彩色时间序列粒子体积3.1 场重构3.1.1 密度场 Φ3.1.2 属性字段 θ3.1.3 优化场重建 3.2 树结构构建…...

A类IP介绍
1)A类ip给谁用: 给广域网用,公网ip使用A类地址,作为公网ip时,Ip地址是全球唯一的。 2)基本介绍 ip地址范围 - 理论范围 0.0.0.0 ~127.255.255.255:00000000 00000000 00000000 00000000 ~ 0111…...

HTML5基本语法
文章目录 HTML5基本语法一、基础标签1、分级标题2、段标签3、换行及水平线标签4、文本格式标签 二、图片标签1、格式2、属性介绍 三、音频标签1、格式2、属性介绍 四、视频标签1、格式2、属性介绍 五、链接标签1、格式2、显示特点3、属性介绍4、补充(空链接…...

正则表达式常用表示
视频教程:10分钟快速掌握正则表达式 正则表达式在线测试工具(亲测好用):测试工具 正则表达式常用表示 限定符 a*:a出现0次或多次a:a出现1次或多次a?:a出现0次或1次a{6}:a出现6次a…...

【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】007 - evb-rk3568_defconfig 配置编译全过程
【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】007 - evb-rk3568_defconfig 配置编译全过程 一、编译后目录列表二、make distclean三、生成.config文件:make V=1 ARCH=arm64 CROSS_COMPILE=aarch64-linux-gnu- evb-rk3568_defconfig四、开始编译:CROSS_COMPILE=aarch64-…...

11.1 Go 标准库的组成
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...
【UG\NX二次开发】UF 调用Grip例子(实现Grip调用目标dll)(UF_call_grip)
此例子是对:【UG\NX二次开发】UF 加载调用与卸载目标dll(UF_load_library、UF_unload_library)_ug二次开发dll自动加载-CSDN博客的补充。 ①创建txt文本,编写以下内容(功能:接收路径,调用该路径的dll)。改后缀为Grip文件(.grs)。…...

[算法刷题积累] 两数之和以及进阶引用
两数之和很经典,通常对于首先想到的就是暴力的求解,当然这没有问题,但是我们如果想要追求更优秀算法,就需要去实现更加简便的复杂度。 这里就要提到我们的哈希表法: 我们可以使用unordered_map去实现,也可以根据题目&a…...

pytest+parametrize+yaml实例
# 一、yaml格式 # # yaml是一种数据类型,可以和json之间灵活的切换,支持注释、换行、字符串等。可以用于配置文件或编写测试用例。 # # 数据结构:一般是键值对的方式出现。注意编写时值前面必须有空格,键:(…...
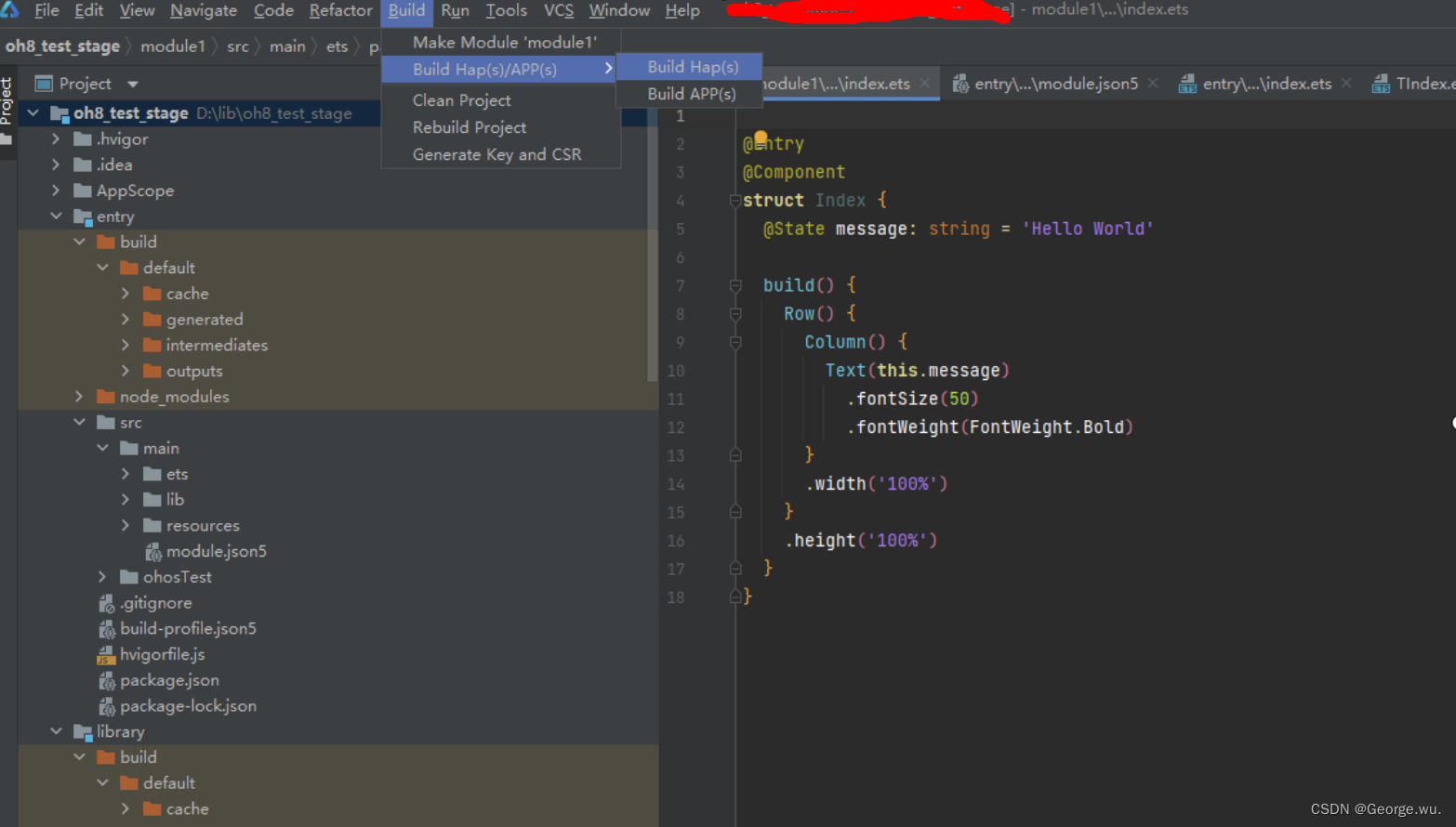
【HarmonyOS】鸿蒙应用模块化实现
【HarmonyOS】鸿蒙应用模块化实现 一、Module的概念 Module是HarmonyOS应用的基本功能单元,包含了源代码、资源文件、第三方库及应用清单文件,每一个Module都可以独立进行编译和运行。一个HarmonyOS应用通常会包含一个或多个Module,因此&am…...

深入Node.js:实现网易云音乐数据自动化抓取
随着互联网技术的飞速发展,数据已成为企业和个人获取信息、洞察市场趋势的重要资源。音频数据,尤其是来自流行音乐平台如网易云音乐的数据,因其丰富的用户交互和内容多样性,成为研究用户行为和市场动态的宝贵资料。本文将深入探讨…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
