九、数据结构(并查集)
文章目录
- 1.并查集操作的简单实现
- 2.解决问题
- 3. 并查集优化
- 3.1 合并的优化
- 3.2查询优化
- 3.3查询优化2
通常用“帮派”的例子来说明并查集的应用背景:在一个城市中有 n ( n < 1 0 6 ) n(n < 10^6) n(n<106)个人,他们分成不同的帮派,给出一些人的关系,例如: 1 1 1号、 2 2 2号是朋友; 1 1 1号、 3 3 3号也是朋友,那么他们都属于一个帮派。在分析完所有的朋友关系之后,问有多少帮派,每人属于哪个帮派。
这个数据量应该是不能用暴力的办法求解,那我们应该怎么办呢?
由此,我们引出一种新的数据结构:并查集
1.并查集操作的简单实现
- 初始化:
定义数组 i n t s [ ] int\ s[\ ] int s[ ] 是以结点 i i i 为元素的并查集,在开始的时候还没有处理点与点之间的朋友关系,所以每个点属于独立的集,并且以元素 i i i 的值表示它的集 s [ i ] s[ i ] s[i],例如元素 1 1 1的集 s [ 1 ] = 1 s[1]=1 s[1]=1。所示为图解,左边给出了元素与集合的值,右边画出了逻辑关系。为了便于讲解,左边区分了结点 i i i 和集 s s s (把集的编号加上了下画线);右边用圆圈表示集,方块表示元素。

- 合并(1):
例如加入第 1 个朋友关系 ( 1 , 2 ) (1,2) (1,2),如下图所示。在并查集s中,把结点 1 合
并到结点 2,也就是把结点 1 的集 1 改成结点 2 的集 2 。
- 合并(2):
加入第 2 2 2 个朋友关系 ( 1 , 3 ) (1,3) (1,3),如下图所示。查找结点 1 1 1 的集是 2 2 2 ,再递归查找元素 2 2 2 的集是 2 2 2 ,然后把元素 2 2 2 的集 2 2 2 合并到结点 3 3 3 的集 3 3 3 。此时,结点 1 1 1、 2 2 2、 3 3 3属于一个集。在图中,为了简化图示,把元素 2 2 2 和集 2 2 2 画在了一起。

- 合并(3):
加入第 3 3 3 个朋友关系 ( 2 , 4 ) (2,4) (2,4), 如图所示。

- 查找:
在上面步骤中已经有查找操作。查找元素的集是一个递归的过程,直到元素的值和它的集相等就找到了根结点的集。从上面的图中可以看到,这棵搜索树的高度可能很大,复杂度是 O ( n ) O_{(n)} O(n)的,变成了一个链表,出现了树的“退化”现象。 - 统计有多少个集:
如果 s [ i ] = i s[ i ] = i s[i]=i,这是一个根结点,是它所在的集的代表。统计根结点的数量,就是集的数量。
2.解决问题
有 n n n 个人一起吃饭,有些人互相认识。认识的人想坐在一起,不想跟陌生人坐。例如 A A A 认识 B B B, B B B 认识 C C C,那么 A A A、 B B B、 C C C会坐在一张桌子上。给出认识的人的关系,问需要多少张桌子。
我们可以根据上文的描述,得到如下并查集代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1007;
int f[N]; //并查集void init(){ //初始化for(int i = 1; i <= N; i++){f[i] = i;}
}int find_father(int x){ //找自己的集if(f[x] == x)return x;else return find_father(f[x]);
}void union_set(int x, int y){ //合并x = find_father(x);y = find_father(y);if(x != y)f[x] = f[y];
}
int main(){init();int n, m, x, y;cin >> n >> m;for(int i = 1; i <= m; i++){cin >> x >> y;union_set(x, y);}int cnt = 0; //记录集的数量for(int i = 1; i <= n; i++){if(f[i] == i){cnt ++;}}cout << cnt;return 0;
}
在上述程序中,查找、合并、的搜索深度是树的长度,复杂度都是 O ( n ) O_{(n)} O(n),性能比较差。下面介绍合并和查找的优化方法,优化之后,查找和合并的复杂度都小于 O ( l o g 2 n ) O(log_2n) O(log2n)。
3. 并查集优化
3.1 合并的优化
在合并元素 x x x和 y y y时先搜到它们的根结点,然后再合并这两个根结点,即把一个根结点的集改成另一个根结点。这两个根结点的高度不同,如果把高度较小的集合并到较大的集上,能减少树的高度。下面是优化后的代码,在初始化时用 h e i g h t [ i ] height[i] height[i] 定义元素 i i i 的高度,在合并时一同更改。
int high[N];
void init(){ //初始化for(int i = 1; i <= N; i++){f[i] = i;high[i] = 0;}
}
void union_set(int x, int y){ //优化合并x = find_father(x);y = find_father(y);if(high[x] == high[y]){high[x]++;f[y] = x;}else{if(high[x] < high[y]){f[x] = y;}else{f[y] = x;}}
}
3.2查询优化
在上面的查询程序 f i n d f a t h e r ( ) find_father() findfather() 中,查询元素 i i i 所属的集需要搜索路径找到根结点,返回
的结果是根结点。这条搜索路径可能很长。如果在返回的时候顺便把 i i i 所属的集改成根结
点,如图所示,那么下次再搜的时候就能在 O ( 1 ) O_{(1)} O(1) 的时间内得到结果。
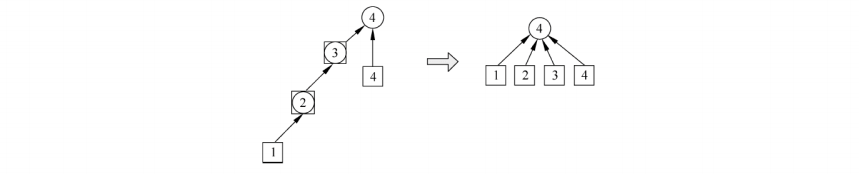
int find_father(int x){ //优化的查询 if(f[x] != x)f[x] = find_father(f[x]); return f[x];
}
这个方法称为路径压缩,因为在递归过程中,整个搜索路径上的元素(从元素 i i i 到根结点的所有元素)所属的集都被改为根结点。路径压缩不仅优化了下次查询,而且优化了合并,因为在合并时也用到了查询。
3.3查询优化2
上面的代码用递归实现,如果数据规模太大,担心爆栈,可以用下面的非递归代码:
int find_father(int x) {int r = x;while (f[r] != r)r = f[r]; //找到根的位置int i = x, j;while(i != r){j = f[i];f[i] = r; //把路径的根统一i = j;}return r;
}
相关文章:

九、数据结构(并查集)
文章目录 1.并查集操作的简单实现2.解决问题3. 并查集优化3.1 合并的优化3.2查询优化3.3查询优化2 通常用“帮派”的例子来说明并查集的应用背景:在一个城市中有 n ( n < 1 0 6 ) n(n < 10^6) n(n<106)个人,他们分成不同的帮派,给出…...

大模型开发技术基础
大模型(Large Model)的开发涉及多个技术基础和领域,涵盖了机器学习、深度学习、自然语言处理(NLP)、计算机视觉(CV)、数据工程等方面。以下是一些关键的技术基础: 1. 机器学习和深度…...

芯片验证分享9 —— 芯片调试
大家好,我是谷公子,之前的课程给大家讲了验证原则、激励设计和代码审查,今天我们来讲芯片调试。 芯片调试是执行一次成功的验证之后要进行的工作。记住,所谓成功的验证,是指它可以证明芯片没有实现预期的功能。调试主…...

java 面试题--基础
文章目录 基础java SE 、 EE 、 ME 的区别jdk 和 jre 区别?java 的日志级别基本数据类型 特性关键字finalabstractsuperswitchfortry catch 接口和抽象类的区别接口抽象类适用场景 类的加载循序静态代码块 传参问题访问修饰符运算符 反射java 里的应用为什么反射的性…...

必看!!! 2024 最新 PG 硬核干货大盘点(上)
PGConf.dev(原名PGCon,从2007年至2023年)首次在风景如画的加拿大温哥华市举办。此次重新定位的会议带来了全新的视角和多项新的内容,参会体验再次升级。尽管 PGCon 历来更侧重于开发者,吸引来自世界各地的资深开发者、…...
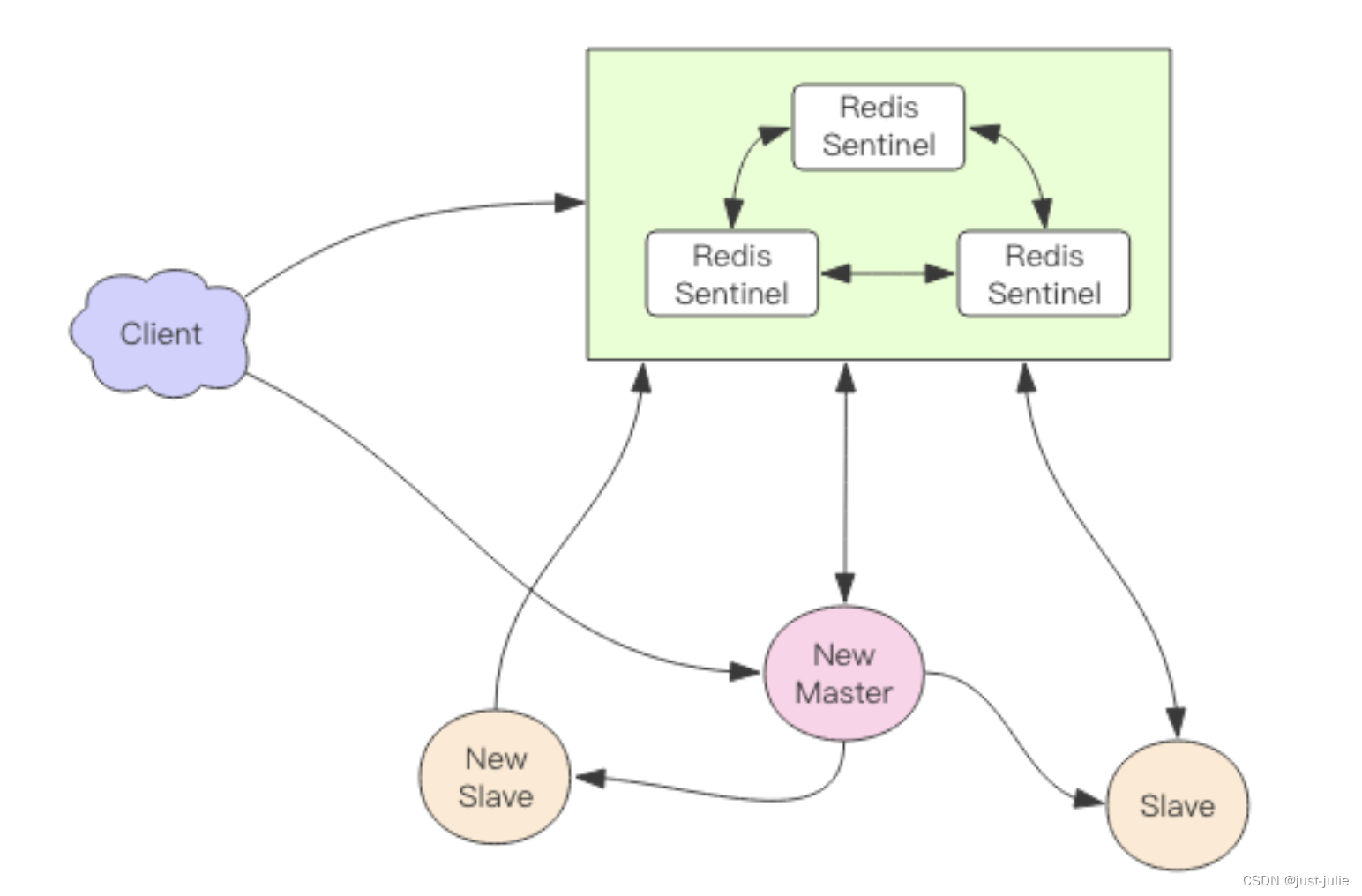
Redis 高可用 sentinel
简介 Sentinel提供了一种高可用方案来抵抗节点故障,当故障发生时Redis集群可以自动进行主从切换,程序可以不用重启。 Redis Sentinel集群可以看成是一个Zookeeper集群,他是Redis集群高可用的心脏,一般由3-5个节点组成࿰…...

【数据结构】练习集
数据的逻辑结构说明数据元素之间的顺序关系,它依赖于计算机的存储结构。(F) 在顺序表中逻辑上相邻的元素,其对应的物理位置也是相邻的。(T) 若一个栈的输入序列为{1, 2, 3, 4, 5},则不可能得到…...

驱动开发(四):Linux内核中断
驱动开发系列文章: 驱动开发(一):驱动代码的基本框架 驱动开发(二):创建字符设备驱动 驱动开发(三):内核层控制硬件层 驱动开发(四…...

btrace:binder_transaction+eBPF+Golang实现通用的Android APP动态行为追踪工具
一、简介: 在进行Android恶意APP检测时,需要进行自动化的行为分析,一般至少包括行为采集和行为分析两个模块。其中,行为分析有基于规则、基于机器学习、基于深度学习甚至基于大模型的方案,各有各的优缺点,不…...

C# OCCT Winform 界面搭建
目录 1.创建一个WInform项目 2.代码总览 代码解析 3.添加模型到场景 4.鼠标交互 1.创建一个WInform项目 2.代码总览 using Macad.Occt.Helper; using Macad.Occt; using System; using System.Collections.Generic; using System.Linq; using System.Runtime.Remoting.Co…...
System.Dynamic.ExpandoObject的使用说明
官方文档 ExpandoObject 类 (System.Dynamic) | Microsoft Learn https://learn.microsoft.com/zh-cn/dotnet/api/system.dynamic.expandoobject?viewnet-8.0 System.Dynamic.ExpandoObject 类 - .NET | Microsoft Learn https://learn.microsoft.com/zh-cn/dotnet/fundame…...

adb之ps命令用法
目录 前言一、命令参数二、输出结果含义 前言 在adb shell终端,输入 ps,可查看手机当前所有的进程状态,其中ps的英文全称是Process Status。 ps命令对于分析系统异常情况时都是必备的技能,需要通过这个简单命令来查看系统真实的状…...
Ubuntu-24.04-live-server-amd64安装界面中文版
系列文章目录 Ubuntu安装qemu-guest-agent Ubuntu-24.04-live-server-amd64启用ssh Ubuntu乌班图安装VIM文本编辑器工具 文章目录 系列文章目录前言一、准备工作二、开始安装三、测试效果总结 前言 Centos结束,转战Ubuntu。我之所以写这篇文章,是因为我…...
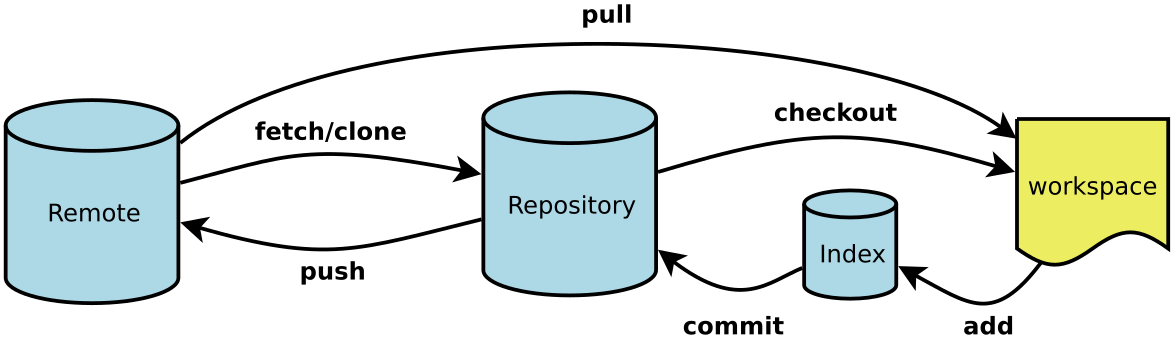
Git的3个主要区域
一般来说,日常使用只要记住下图6个命令,就可以了。但是熟练使用,恐怕要记住60~100个命令。 下面是我整理的常用 Git 命令清单。几个专用名词的译名如下。 Workspace:工作区 Index / Stage:暂存区 Reposito…...
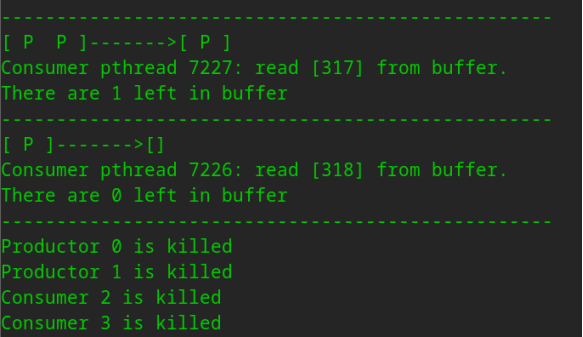
【操作系统】操作系统实验02-生产者消费者程序改进
1. 说明文档中原有程序实现的功能、实现方法。(用语言、程序流程图、为原有程序添加注释等方式均可) 1.//const.h 2.//定义宏变量 3.#ifndef CONST_H 4.#define CONST_H 5. 6.#define TRUE 1 7.#define FALSE 0 8.#define ERROR 0 9.#define OVERFLOW -…...

TCP协议是安全的吗?
不安全 虽然 TCP 提供了一种可靠且高效的数据传输方式,但它不提供任何加密或身份验证机制来保护数据。因此,传输的数据可能会被未经授权的用户拦截和读取,而且其真实性无法验证。 因此,为了确保 TCP 通信的安全,必须…...

c语言回顾-结构体(2)
前言 前面讲了结构体的概念,定义,赋值,访问等知识,本节内容小编将讲解结构体的内存大小的计算以及通过结构体实现位段,话不多说,直接上干货!!! 1.结构体内存对齐 说到计…...
Prometheus常见exporter安装部署
Prometheus常见exporter安装部署 在稳定性环境的监控当中需要收集各种各样的数据,这样的数据收集是通过各种exporter进行的,在这里我们进行最常用稳定性数据的收集exporter安装部署介绍。 node_exporter安装部署 node_exporter主要监控服务器本身的一…...
DGit的使用
将Remix连接到远程Git仓库 1.指定克隆的分支和深度 2.清理,如果您不在工作区上工作,请将其删除或推送至 GitHub 或 IPFS 以确保安全。 为了进行推送和拉取,你需要一个 PAT — 个人访问令牌 当使用 dGIT 插件在 GitHub 上推送、拉取、访问私…...
ElasticSearch学习篇13_《检索技术核心20讲》进阶篇之LSM树
背景 学习极客实践课程《检索技术核心20讲》https://time.geekbang.org/column/article/215243,文档形式记录笔记。 内容 磁盘和内存数据读取特点 工业界中数据量往往很庞大,比如数据无法全部加载进内存,无法支持索引的高效实时更新&…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
