「动态规划」如何求粉刷房子的最少花费?
LCR 091. 粉刷房子![]() https://leetcode.cn/problems/JEj789/description/
https://leetcode.cn/problems/JEj789/description/
假如有一排房子,共n个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。当然,因为市场上不同颜色油漆的价格不同,所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个n x 3的正整数矩阵costs来表示的。例如,costs[0][0]表示第0号房子粉刷成红色的成本花费;costs[1][2]表示第1号房子粉刷成绿色的花费,以此类推。请计算出粉刷完所有房子最少的花费成本。
- 输入:costs = [[17,2,17],[16,16,5],[14,3,19]],输出:10,解释:将0号房子粉刷成蓝色,1号房子粉刷成绿色,2号房子粉刷成蓝色。最少花费:2 + 5 + 3 = 10。
- 输入:costs = [[7,6,2]],输出:2
提示:costs.length == n,costs[i].length == 3,1 <= n <= 100,1 <= costs[i][j] <= 20。
我们用动态规划的思想来解决这个问题。
确定状态表示:根据经验和题目要求,我们用dp[i]表示粉刷完i位置的房子后,此时的最少花费。这可以细分为:
- 用dp[i][0]表示:将i位置的房子粉刷成红色之后的最少花费。
- 用dp[i][1]表示:将i位置的房子粉刷成蓝色之后的最少花费。
- 用dp[i][2]表示:将i位置的房子粉刷成绿色之后的最少花费。
简单来说,在dp[i][j]中,i表示最后一个粉刷的房子的编号;j表示最后一个粉刷的房子中,粉刷的颜色的编号;dp[i][j]表示此时的最少花费。
推导状态转移方程:我们考虑最近的一步,即粉刷完i - 1位置的房子之后的情况。
- 考虑dp[i][0]。把i位置的房子粉刷成红色,所以只能把i - 1位置的房子粉刷成蓝色或者绿色。那么,把i位置的房子粉刷成红色之后的最少花费,就应该是把i - 1位置的房子粉刷成蓝色或者绿色之后的最少花费,两种情况的较小值,再加上把i位置粉刷成红色的花费。即dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0]。
- 同理,dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1],dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i][2]。
综上所述:dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i][0],dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i][1],dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i][2]。
初始化:根据状态转移方程,在计算dp[0][j],其中j的范围是[0, 2]时,会发生越界访问,所以要进行相应的初始化。
- dp[0][0]表示把0位置的房子粉刷成红色后,此时的最少花费,显然dp[0][0] = costs[0][0]。
- 同理dp[0][1] = costs[0][1],dp[0][2] = costs[0][2]。
综上所述:dp[0][0] = costs[0][0],dp[0][1] = costs[0][1],dp[0][2] = costs[0][2]。
当然,我们可以在最前面添加一个辅助结点dp[0][j] = 0,其中j的范围是[0, 2]。这样,根据状态转移方程,以dp[i][0]为例,此时min(dp[0][1], dp[0][2]) = 0,辅助结点的值不影响结果,符合预期。
填表顺序:根据状态转移方程,对于dp[i][j]只依赖于dp[i - 1][j],j的范围是[0, 2]。那么,我们只需要沿着i增大的方向填表。
返回值:由于不确定把最后一个房子粉刷成什么颜色,根据状态表示,最终应返回把最后一个房子粉刷成红色、蓝色或者绿色这3种情况中,最少花费的最小值,即dp[n][j]的最小值,其中j的范围是[0, 2]。
细节问题:由于新增了一个辅助结点,此时dp表的规模就不是n x 3,而是(n + 1) x 3。同时需注意下标的映射关系,dp[i][j]对应的是costs[i - 1][j]。
时间复杂度:O(N),空间复杂度:O(N)。
class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();// 创建dp表vector<vector<int>> dp(n + 1, vector<int>(3));// 填表for (int i = 1; i <= n; i++) {dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2];}// 返回结果return min(dp[n][0], min(dp[n][1], dp[n][2]));}
};相关文章:
「动态规划」如何求粉刷房子的最少花费?
LCR 091. 粉刷房子https://leetcode.cn/problems/JEj789/description/ 假如有一排房子,共n个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。当然,因为市…...

代码随想录算法训练营DAY41|背包问题 二维 、背包问题 一维、416. 分割等和子集
背包问题 二维 题目链接:背包问题 二维 def bag_weight_problem(n,space,weight,value):dp [[0 for i in range(space1)]for j in range(n)]for i in range(weight[0], space1):dp[0][i]value[0]for j in range(1, n):for k in range(space1):if weight[j]>k:…...
gitlab2024最新版安装
系统:redhat9.0 gitlab版本:gitlab-ce-16.10.7-ce.0.el9.x86_64.rpm 安装组件&包依赖:https://packages.gitlab.com/gitlab/gitlab-ce/packages/ol/9/gitlab-ce-16.10.7-ce.0.el9.x86_64.rpm 参考: 前提: 下载gitl…...

2022C语言二级真题
目录 数组逆序重放 题目描述 样例 最长最短单词 题目描述 样例 统计误差范围内的数 题目描述 样例 有趣的跳跃 题目描述 样例 数字放大 题目描述 样例 内部元素之和 题目描述 样例 满足条件的数的累加 题目描述 样例 偶数降序输出 题目描述 样例 字符统…...

智慧购房:链家网上海在售楼盘数据解析与模型构建
1.项目背景 随着中国经济的快速发展,上海作为国际化大都市,其房地产市场一直备受关注,购房者在面对庞大且复杂的楼盘信息时,往往感到困惑和不知所措,为了帮助购房者更好地了解市场行情,做出明智的购房决策,本项目选择了链家网上海市在售楼盘数据,进行了全面的数据分析…...
二进制数转字符串
题目链接 二进制数转字符串 题目描述 注意点 32位包括输出中的 “0.” 这两位题目保证输入用例的小数位数最多只有 6 位 解答思路 将小数转为二进制的思路是将小数乘2,如果整数部分为1,则说明第i位是1(第i位则乘了2的几次方)…...

WINDOWS系统jdk和maven明明安装了cmd里却无法使用相关命令
今天当了回s b 新电脑jdk和maven装是装了,系统变量也配置了,但没配置完,javahome和mavenhome没配置,结果cmdjdk和maven版本都查不到,我真s b啊 配置 JAVA_HOME 环境变量: 右键点击“此电脑”或者“我的电…...
基于EasyAnimate模型的视频生成最佳实践
EasyAnimate是阿里云PAI平台自主研发的DiT的视频生成框架,它提供了完整的高清长视频生成解决方案,包括视频数据预处理、VAE训练、DiT训练、模型推理和模型评测等。本文为您介绍如何在PAI平台集成EasyAnimate并一键完成模型推理、微调及部署的实践流程。 …...
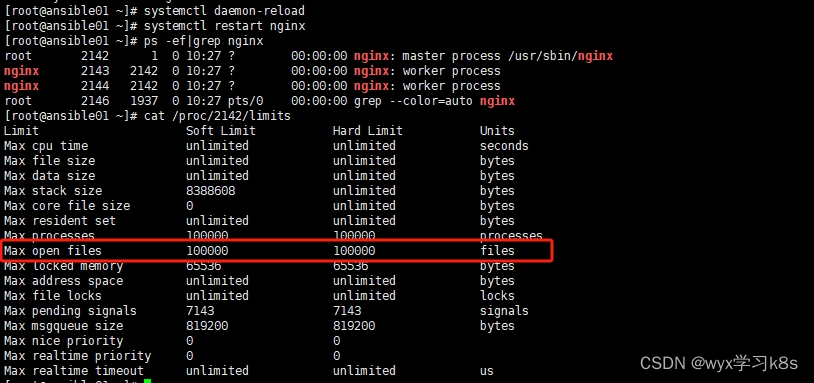
linux最大线程数限制及打开最大文件数
1.root用户下执行 ulimit -a 然后查看 max user processes 这个值通常是系统最大线程数的一半 max user processes:当前用户同时打开的进程(包括线程)的最大个数为 2.普通用户下 ulimit -a 出现的max user processes的值 默认是 /etc/security/limits.d/20-nproc.co…...

MyBatis系列七: 一级缓存,二级缓存,EnCache缓存
缓存-提高检索效率的利器 官方文档 一级缓存基本介绍快速入门Debug一级缓存执行流程一级缓存失效分析 二级缓存基本介绍快速入门Debug二级缓存执行流程注意事项和使用细节 mybatis的一级缓存和二级缓存执行顺序小实验细节说明 EnCache缓存基本介绍配置和使用EhCache细节说明 My…...

C++迈向精通:函数指针对象与函数对象
C:指针对象 C语言中的函数指针 在C语言中,我们见过如下的函数指针: int add(int a, int b) {return a b; }int main() {int a, b;int (*p)(int, int) add;scanf("%d%d", &a, &b);p(a, b);return 0; } 为了适应C中面向…...

类和对象知识点
面向对象概念回顾 万物皆对象 用程序来抽象(形容)对象 用面向对象的思想来编程 什么是类 基本概念 具有相同特征,具有相同行为,一类事物的抽象。 类是对象的模板,可以通过类创建出对象,类的关键词—…...

【FAS】《Survey on face anti-spoofing in face recognition》
文章目录 原文基于手工设计特征表达的人脸活体检测方法基于深度学习的人脸活体检测方法基于融合策略的人脸活体检测方法人脸检测活体数据库点评 原文 邓雄,王洪春,赵立军等.人脸识别活体检测研究方法综述[J].计算机应用研究,2020,37(09):2579-2585.DOI:10.19734/j.issn.1001-3…...

【Unity】RPG2D龙城纷争(一)搭建项目、导入框架、前期开发准备
更新日期:2024年6月12日。 项目源码:后续章节发布 免责声明:【RPG2D龙城纷争】使用的图片、音频等所有素材均有可能来自互联网,本专栏所有文章仅做学习和教程目的,不会将任何素材用于任何商业用途。 索引 【系列简介】…...

多目标跟踪中检测器和跟踪器如何协同工作的
多目标跟踪中检测器和跟踪器如何协同工作的 flyfish 主要是两者 接口间的交互 假设 原始图像尺寸:1920(宽)x 1080(高) 模型输入尺寸:640(宽)x 640(高) 检…...

kali系统几个开机启动项的区别
1、Live system (amd64) 简单的模式 ,启动系统,直接进入 Kali,在系统中的所有的操作和设置都会在下次重启时失效。 Kali 中保存/编辑的所有东西都会重启丢失。 2、Live system (amd64 fail-safe mode) 这种模式与 Live (amd64) 类似…...

【自撰写】【国际象棋入门】第5课 常见开局战术组合(一)
第5课 常见开局战术组合(一) 本次课中,我们简要介绍几种常见的开局战术组合。开局当中,理想的情况是,己方的两只(或以上)轻子相互配合,或者与己方的兵配合,在完成布局的…...

高考志愿填报选专业,女孩就业率最好的专业有哪些?
高考志愿填报选专业, 大家都会关心:将来怎么就业? 按照目前的环境来说,女孩的就业是不乐观的,在职场上,绝大部分岗位都是男性优先的,至少短期内可能还无法改变,这样就要求我们在大学…...

yolov5模型训练早停模型变大
目录 1. 背景2. 原因分析2.1 train代码分析2.2 strip_optimizer函数分析 3. 验证 1. 背景 最近使用tph-yolov5训练yolov5l-tph-plus模型时,发现模型收敛的差不多了,就果断的停止了训练,结果发现last.pt和best.pt竟然488M,而正常训…...

next是什么???
大家都知道最近出了一个很火的框架,Next.js框架。很多大公司(例如:Tencent腾讯,docker,Uber)的项目都在使用这个Next.js框架。那Next.js到底是一个什么框架呢?Next.js有什么优点呢?今…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
