【C语言】数据结构-二叉树
主页:114514的代码大冒险
qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ )
Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com
引入
我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树
望文生义,这个数据结构肯定与现实中的树, 有着一定的联系,如图:
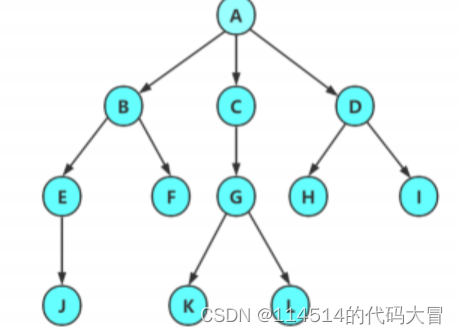

数据结构中的树它看起来像树枝,也想树的根部
树的概念

树的相关概念
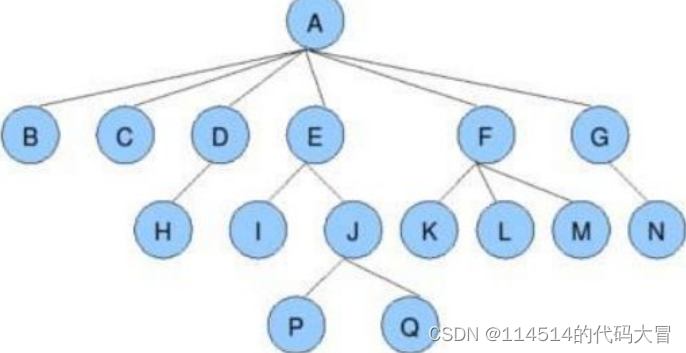
节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的为6叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I...等节点为叶节点非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G...等节点为分支节点双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点树的度:一棵树中,最大的节点的度称为树的度;如上图:树的度为6节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;树的高度或深度:树中节点的最大层次;如上图:树的高度为4堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙森林:由m(m>0)棵互不相交的树的集合称为森林;
树的表示
概念图:

树在实际中的运用(表示文件系统的目录树结构)
文件目录:

公司内部功能安排
二叉树(特殊的树)
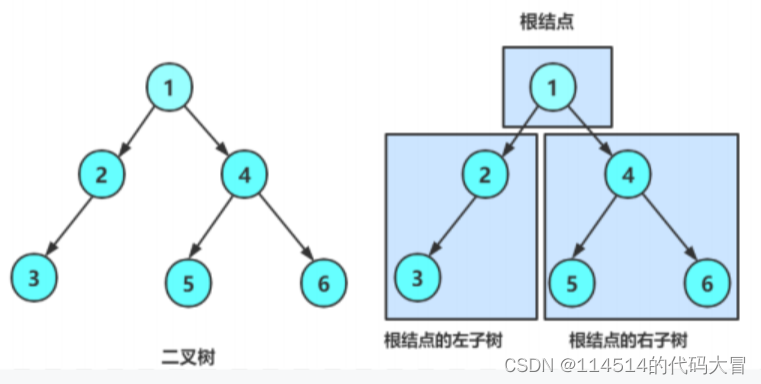

这些都不重要
你只需要知道二叉树的每个节点最多两个孩子
可以没有孩子,也可以只有一个孩子
另外在二叉树中
左孩子和右孩子是有差异的
现实中的二叉树


1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k-1,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
说人话:
就是说如果除了最底下那一排(所谓的叶子节点)其他的节点都有两个孩子
我们就称之为满二叉树

那么什么是完全二叉树呢
就是除了树的倒数第二排之外,其他节点都有两个孩子
如图: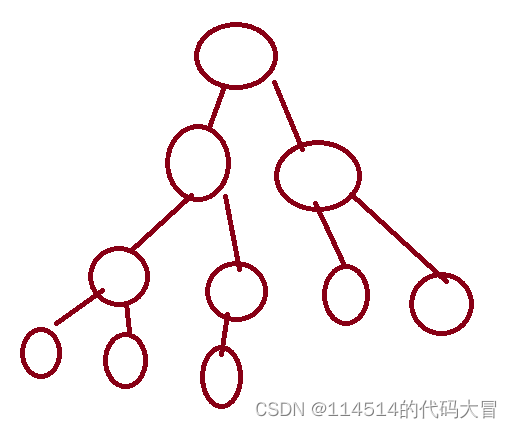
二叉树的性质


说了一大堆,能看懂多少算多少
我来说几个比较可能用到的点
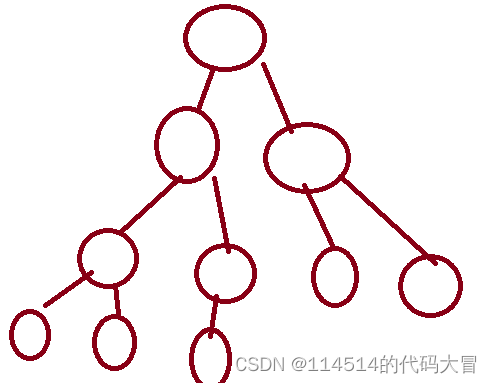 只要是树,有两个孩子的节点始终比没有孩子的节点的数量少一
只要是树,有两个孩子的节点始终比没有孩子的节点的数量少一
完全二叉树的坐标规律如右图所示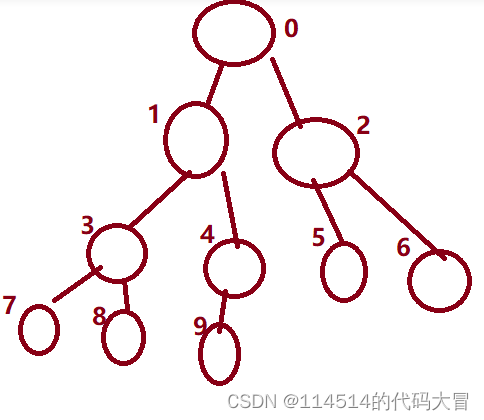
(完全二叉树中) 我们假使某节点这个下标为i,那么它的父亲就是
(i-1)/2 ,左孩子(如果有的话)为2*i+1,右孩子为左孩子坐标加1
另外还有就是这个完全二叉树的层数问题
除开最后一层外,第一层节点的数量为2^0,第二次为2^1第三次为2^2
第n层为2^(n-1),
如此满二叉树的节点数量为2^n - 1个
hhh,非满二叉树的节点数量则为前n-1层的节点数量+最后一层的节点数
我想,这个时候,在知道二叉树的节点的数量前提下
求出二叉树的深度,也就是层数不是什么困难的事情了
总结
这就是今天的树的概念讲解
这部分内容不需要太过焦虑
这些概念现在只是稍微有个大概就可以
我们在接下来的学习中会反复提到
相关文章:

【C语言】数据结构-二叉树
主页:114514的代码大冒险 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 引入 我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树 树是一种非线性的…...

c++中std::condition_variable最全用法归纳
前言 建议阅读以下文章前需先对建立 std::thread 多线程与std::mutex 锁有一定程度的熟悉 std::thread最全用法归纳 std::mutex最全用法归纳 概括 使用 std::condition_variable 的 wait 会把目前的线程 thread 停下来并且等候事件通知,而在另一个线程中可以使用…...

Python数据可视化:数据关系图表可视化
目录 1、散点图 1.1、趋势显示的二维散点图 1.2、分布显示的二维散点图 1.3、散点曲线图...

Urho3D约定
Urho3D使用以下约定和原则: 左手坐标系。正X、Y和Z轴指向右侧、上方和前方,正旋转为顺时针。度用于角度。顺时针顶点定义正面。音频音量指定为0.0(静音)到1.0(全音量)路径名使用斜杠而不是反斜杠。调用操作…...

python数据结构-列表,元组
列表 列表是Python中最通用的数据类型,可以写成方括号之间的逗号分隔值(项目)列表。 使用列表的重要事项是,列表中的项目不必是相同的类型。也就是说一个列表中的项目(元素)可以是数字,字符串,数组,字典等甚至是列表类…...
Properties类读配置文件、修改配置文件
Properties类简介(1)Properties类是专门用于读写配置文件的集合类(2)配置文件的后缀名为.properties,内容格式为:# 可以用“#”作为注释 键值 键值**注意:**键值对不需要有空格,值不需要用引号一起来。默认类型是String。键、值不可以是null(3)Properties类的方法可查找api文档…...
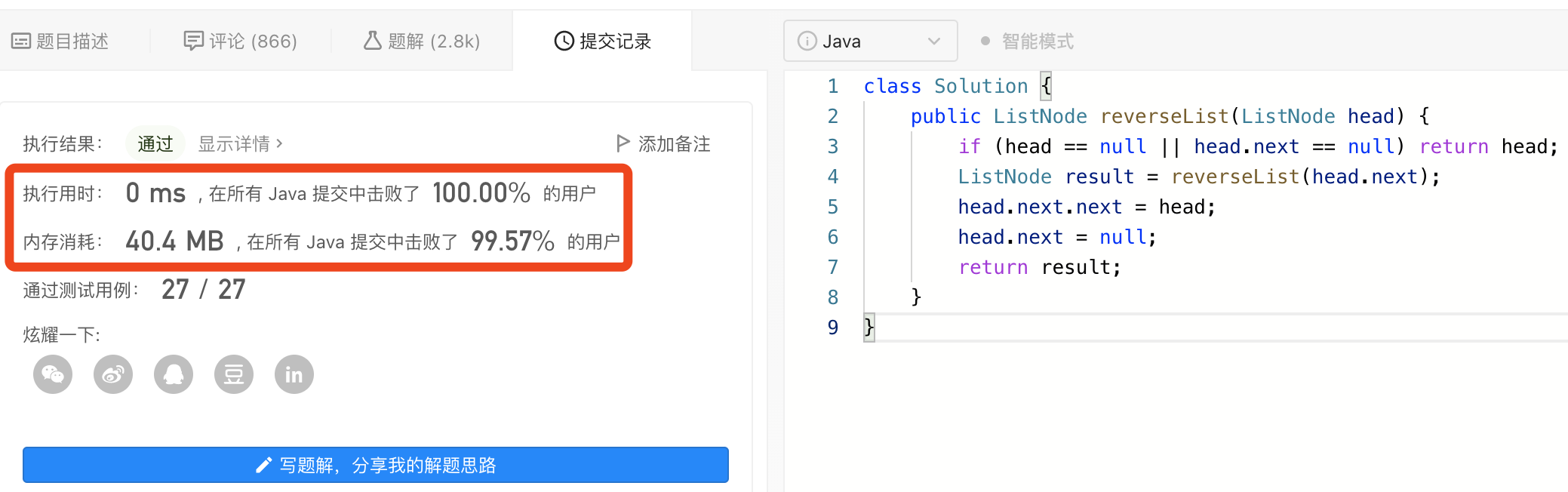
图解LeetCode——剑指 Offer 24. 反转链表
一、题目 定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。 二、示例 示例: 【输入】 1->2->3->4->5->NULL 【输出】 5->4->3->2->1->NULL 限制: 0 < 节点个数 < 5000 三、…...

【C语言】“指针的运算”、“指针与数组”
文章目录一、指针运算1.指针 - 整数2.指针-指针3.指针关系运算二、指针与数组三、二级指针四、指针数组完结一、指针运算 指针可以进行整数,指针-指针,还有关系运算,其他的运算会被编译器阻止。 1.指针 - 整数 对指针进行的时候一定要注意不…...
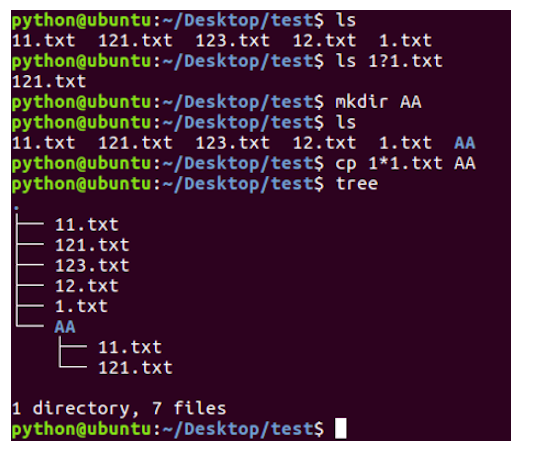
Linux高级命令之查找文件命令
查找文件命令学习目标能够说出查找文件使用的命令1. find命令及选项的使用命令说明find在指定目录下查找文件(包括目录)find命令选项:选项说明-name根据文件名(包括目录名)字查找find命令及选项的效果图:2. find命令结合通配符的使用通配符:是一种特殊语句,主要有星…...

PyCharm+Docker:打造最舒适的深度学习炼丹炉
九、PyCharmDocker:打造最舒适的深度学习炼丹炉 安装docker: 如何在 Ubuntu 22.04 LTS 中安装 Docker 和 Docker Compose https://zhuanlan.zhihu.com/p/547169542 修改Linux硬盘卷标: ntfs文件系统:https://blog.csdn.net/n…...
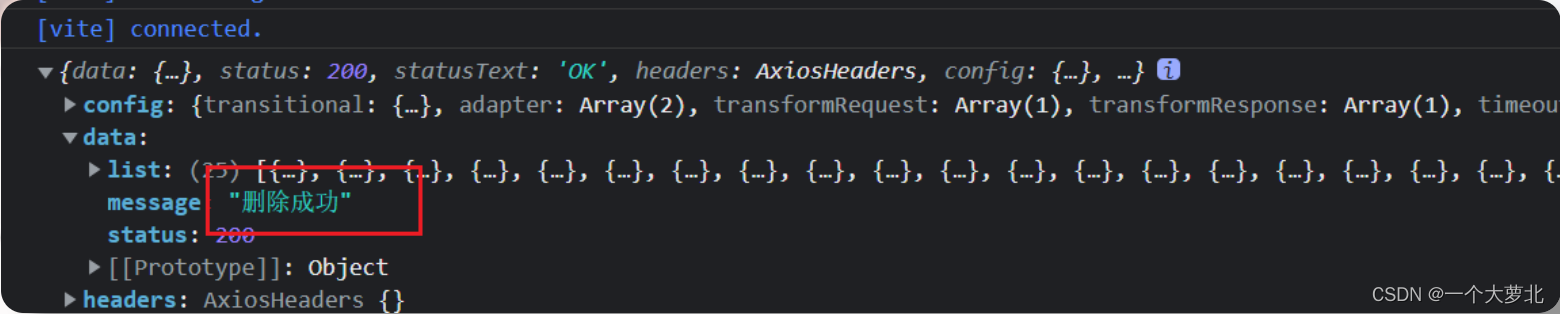
【mock】手把手带你用mock写自定义接口+mock常用语法
mock自定义接口完整流程 官网语法规范:https://github.com/nuysoft/Mock/wiki/Syntax-Specification 首先: 要有一个项目,我这里是vue3项目,以下从vue3项目搭建开始,已搭建好的请直接看2 1.空目录下新建vue3项目 运行创建项目命令: 在bash中:(文件路径处输入cm…...

2023 年腾讯云服务器CVM快速配置购买教程,新手上云必备!
腾讯云服务器快速配置购买教程是新手必备的上云教程。主机教程网在本文中以腾讯云服务器为例,给大家带来一个完整的、手把手教学的服务器购买流程。助力快速完成服务器的购买、配置、以及网站的搭建,给新手节省宝贵的时间,避免采坑࿰…...

opencv显示图像
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

C++:类和对象(中)
文章目录1 类的6个默认成员函数2 构造函数2.1 概念2.2 特性3 析构函数3.1 概念3.2 特性4 拷贝构造函数4.1 概念4.2 特性5 赋值运算符重载5.1 运算符重载5.2 赋值运算符重载5.3 前置重载和后置重载6 日期类的实现7 const成员8 取地址及const取地址操作符重载1 类的6个默认成员函…...
53. 最大子数组和
文章目录题目描述暴力法动态规划法分治法参考文献题目描述 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入&…...

基于Java+SpringBoot+SpringCloud+Vue前后端分离医院管理系统设计与实现
博主介绍:✌全网粉丝3W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建、毕业项目实战、项目定制✌ 博主作品:《微服务实战》专栏是本人的实战经验总结,《S…...

QT基础入门【环境配置篇】linux桌面QT开发环境的构建以及问题解决
目录 一、下载QT的安装包 二、安装 1.执行以下命令开始安装 2.选择配置 三、启动...

Linux系统之部署企业内部静态导航页
Linux系统之部署企业内部静态导航页 一、本次实践目的二、检查本地系统环境1.检查系统版本2.检查内核版本三、下载静态导航页资源包1.创建下载目录2.下载资源包四、安装apache服务1.安装httpd2.复制网页文件3.重启httpd服务4.检查httpd服务状态五、访问导航页六、修改导航页网站…...
)
2023备战金三银四,Python自动化软件测试面试宝典合集(四)
接上篇:11、点击塞钱进红包,选择使用新卡付款,按照流程添加新卡,此时同样需要考虑金额>新卡余额,金额<新卡余额,金额新卡余额三种情况12、使用指纹确认付款(正确的/不正确的指纹)13、使用密码确认付款…...

算法训练营 day43 动态规划 不同路径 不同路径 II
算法训练营 day43 动态规划 不同路径 不同路径 II 不同路径 62. 不同路径 - 力扣(LeetCode) 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

