C++回溯算法(2)
棋盘问题
#include<bits/stdc++.h>
using namespace std;
void func(int,int);
bool tf(int,int);
void c();
int n,k;
char a[110][110];
int cnt2=0;
int main()
{cin>>n>>k;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>a[i][j];}}func(0,0);cout<<"----------"<<endl;cout<<cnt2;return 0;
}
void func(int x,int cnt)
{if(cnt==k){c();cnt2++;return;}if(x==n){return;}for(int i=0;i<n;i++){if(tf(x,i)==true&&a[x][i]!='.'){a[x][i]='o';func(x+1,cnt+1);a[x][i]='.';}}func(x+1,cnt);
}
bool tf(int x,int y)
{for(int i=0;i<x;i++){if(a[i][y]=='o'){return false;}}return true;
}
void c()
{cout<<"----------"<<endl;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cout<<a[i][j];}cout<<endl;}
}相关文章:

C++回溯算法(2)
棋盘问题 #include<bits/stdc.h> using namespace std; void func(int,int); bool tf(int,int); void c(); int n,k; char a[110][110]; int cnt20; int main() {cin>>n>>k;for(int i0;i<n;i){for(int j0;j<n;j){cin>>a[i][j];}}func(0,0);cout…...

流量有限、日活低的APP适合对接广告变现吗?
APP广告变现,总用户数和日活用户(DUA)是衡量APP价值和影响力的重要指标之一。 APP DUA过万,尤其是大几万时,通常具备了商业化价值,适合接入广告变现。日活1W意味着每天有1万名用户在使用这款应用ÿ…...

Shell 学习笔记 - 变量的类型 + 变量的赋值
1.6 Shell 变量的类型 Shell 变量分为四类,分别是 自定义变量环境变量位置变量预定义变量 根据工作要求临时定义的变量称为自定义变量; 环境变量一般是指用 export 内置命令导出的变量,用于定义 Shell 的运行环境,保证 Shell …...

vue播放flv格式的直播流
在ios无法播放,安卓可以 安装 npm install flv.js --save页面 <template><div><videoref"videoElement"style"width: 100%; height: 100%"autoplayplaysinlinemuted></video></div> </template><scr…...

Qt入门小项目 | 实现一个图片查看器
文章目录 一、实现一个图片查看软件 一、实现一个图片查看软件 需要实现的功能: 打开目录选择图片显示图片的名字显示图片 在以上功能的基础上进行优化,需要解决如下问题: 如何记住上次打开的路径? 将路径保存到配置文件中&#x…...
qt仿制qq登录界面
#include "mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent) {// 设置窗口大小this->resize(window_width, window_heigth);// 固定窗口大小this->setFixedSize(window_width, window_heigth);// 设置窗口图标this->se…...

HashMap详解(含动画演示)
目录 HashMap1、HashMap的继承体系2、HashMap底层数据结构3、HashMap的构造函数①、无参构造②、有参构造1 和 有参构造2 (可以自定义初始容量和负载因子)③、有参构造3(接受一个Map参数)JDK 8之前版本的哈希方法:JDK 8版本的哈希方法 4、拉链法解决哈希冲突什么是拉…...

TVS的原理及选型
目录 案例描述 TVS管的功能与作用: TVS选型注意事项: 高速TVS管选型 最近项目中遇到TVS管选型错误的问题。在此对TVS的功能及选型做一个分享。 案例描述 项目中保护指标应为4-14V,而选型的TVS管位SMJ40CA,其保护电压为40V未…...

【机器学习】无监督学习:探索数据背后的隐藏模式
在机器学习的广阔领域中,监督学习因其直观的训练方式和广泛的应用场景,往往受到更多的关注。然而,随着数据量和数据类型的不断增长,无监督学习的重要性日益凸显。本文将详细介绍无监督学习的理论基础、常用算法及其在实际中的应用…...

使用Elasticsearch在同一索引中区分不同类型的文档
在使用Elasticsearch时,有时我们需要在同一个索引中存放不同类型的文档,并且这些文档的字段可能不一致。在早期版本中,我们可以使用types来实现,但在Elasticsearch 7.x及更高版本中,types概念已被弃用。本文将介绍如何…...
驾校在线考试系统源码 手机+PC+平板自适应
Thinkphp在线考题源码 驾校在线考试系统 手机PC平板 自适应,机动车驾驶培训学校驾校类网站源码带手机端 运行环境:phpmysql 内附安装说明 驾校在线考试系统源码 手机PC平板自适应...

c++的多态,继承,抽象类,虚函数表,虚函数等题目+分析
目录 题目 代码题 分析 主观题 题目 代码题 class A { public:virtual void func(int val 1) {std::cout << "A->" << val << std::endl;}virtual void test() { func(); } };class B : public A { public:void func(int val 0) { std…...

利用 Qwen-VL 进行私有化部署第一个 AI 多模态大模型
Hi~!这里是奋斗的小羊,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~ 💥💥个人主页:奋斗的小羊 💥💥所属专栏:C语言 🚀本系列文章为个人学习…...

王思聪隐形女儿曝光
王思聪"隐形"女儿曝光!黄一鸣独自面对怀孕风波,坚持生下爱情结晶近日,娱乐圈掀起了一场惊天波澜!前王思聪绯闻女友黄一鸣在接受专访时,大胆揭露了她与王思聪之间的爱恨纠葛,并首度公开承认&#…...
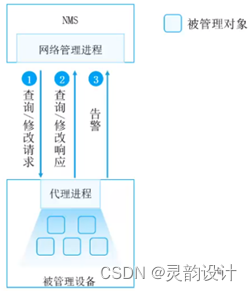
学习笔记——网络管理与运维——SNMP(SNMP原理)
四、SNMP原理 SNMP的工作原理基于客户端-服务器模型。其中,网络管理系统是客户端,而网络设备是服务器。客户端向服务器发送请求消息(即"Get"或"Set"命令)来获取或修改服务器的信息。服务器收到请求消息后,会返回相应的响…...
基于STM32和人工智能的自动驾驶小车系统
目录 引言环境准备自动驾驶小车系统基础代码实现:实现自动驾驶小车系统 4.1 数据采集模块4.2 数据处理与分析4.3 控制系统4.4 用户界面与数据可视化应用场景:自动驾驶应用与优化问题解决方案与优化收尾与总结 1. 引言 随着人工智能和嵌入式系统技术的…...
简单介绍vim
文章目录 前言一、Vim的特点二、安装Vim三、设置Vim配置文件的位置:编辑配置文件:添加配置选项:保存并退出编辑器:快速配置验证设置: 总结 前言 Vim是一款强大的文本编辑器,被广泛用于各种编程和文本编辑任…...

使用本地数据对transformers模型进行微调训练
模型 transformers模型是使用比较多的模型,奈何各个都是体积大,找了一个使用人多不是很大的模型进行训练。 需要魔法 bert-base-uncased模型仓库地址 huggingface下的所有仓库都是git的,也就意味着你可以使用 git clone 可以下载仓库内所有的…...

Java面试题:讨论何时需要创建自定义异常类,并展示如何实现一个自定义异常
在Java中,创建自定义异常类的目的是为了更加清晰和有意义地表示特定的错误情况,增强代码的可读性和可维护性。以下是一些需要创建自定义异常类的常见场景以及如何实现一个自定义异常。 何时需要创建自定义异常类 特定业务逻辑错误: 当业务逻…...

什么是进程
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 在了解进程之前,我们需要知道多任务的概念。多任务,顾名思义,就是指操作系统能够执行多个任务。例如,…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
