【LeetCode最详尽解答】11-盛最多水的容器 Container-With-Most-Water
欢迎收藏Star我的Machine Learning Blog:https://github.com/purepisces/Wenqing-Machine_Learning_Blog。如果收藏star, 有问题可以随时与我交流, 谢谢大家!
链接:
- 11-盛最多水的容器
直觉
这个问题可以通过可视化图表来理解和解决。
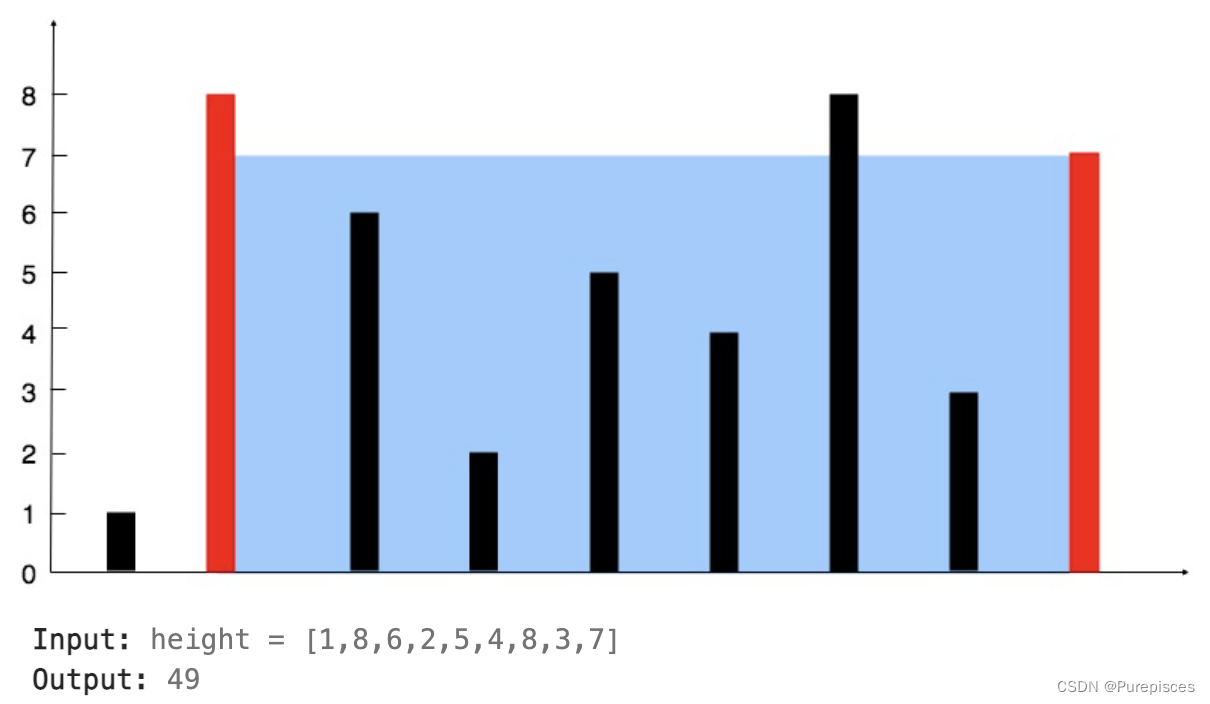
通过图形化这个问题,可以简化解决过程。我们可以使用双指针技术来解决它。起初,左指针设置在数组的起点,右指针设置在数组的终点。目标是找到最大的可能面积,这个面积受指针指向的较短高度的限制。面积可以通过公式 min(height[left], height[right]) * (right - left) 计算。容器的高度受较短的两个高度之一限制。
为了最大化面积,我们应该移动指向较短高度的指针。这是因为移动指向较高高度的指针不会有助于找到更大的面积,因为容器的高度仍然会受较短高度的限制。具体来说,新高度将是 min(height[left], height[new_right]),它将小于或等于之前的较短高度,并且间隔距离也会缩小。因此,如果左指针指向较短高度,我们将其向右移动。相反,如果右指针指向较短高度,我们将其向左移动。
方法
- 初始化两个指针:左指针在数组起点,右指针在数组终点。
- 初始化一个变量
res来存储最大面积。 - 使用公式
res = max(res, min(height[left], height[right]) * (right - left))来计算面积并更新res。 - 移动指向较短高度的指针以尝试找到更大的面积。
- 设置提前停止条件:设
h为数组中的最大高度。如果(right - left) * h小于res,则意味着不可能找到更大的面积,因此我们可以跳出循环。
复杂度
- 时间复杂度:
O ( n ) O(n) O(n)- 我们只用两个指针遍历数组一次,时间复杂度为线性。
- 空间复杂度:
O ( 1 ) O(1) O(1)- 无论输入大小如何,我们只使用了常量空间。
代码
class Solution(object):def maxArea(self, height):""":type height: List[int]:rtype: int"""l = 0r = len(height) -1h = max(height)res = 0while l < r:if (r-l) * h <= res:breakres = max(res, min(height[l],height[r]) * (r-l))if height[l] <= height[r]:l+=1elif height[l] > height[r]:r-=1return res
相关文章:

【LeetCode最详尽解答】11-盛最多水的容器 Container-With-Most-Water
欢迎收藏Star我的Machine Learning Blog:https://github.com/purepisces/Wenqing-Machine_Learning_Blog。如果收藏star, 有问题可以随时与我交流, 谢谢大家! 链接: 11-盛最多水的容器 直觉 这个问题可以通过可视化图表来理解和解决。 通过图形化这个…...

redis 缓存jwt令牌设置更新时间 BUG修复
大家好,今天我又又又来了,hhhhh。 上文中 我们永redis缓存了token 但是我们发现了 一个bug ,redis中缓存的token 是单用户才能实现的。 就是 我 redis中存储的键 名 为token 值 是jwt令牌 ,但是如果 用户a 登录 之后 创建一个…...

nginx精准禁止特定国家或者地区IP访问
1、安装依赖 dnf -y install gcc-c libtool gd-devel pcre pcre-devel openssl openssl-devel zlib zlib-devel libmaxminddb-devel pcre-devel zlib-devel gcc gcc-c make git2、获取NGINX安装包并安装 wget https://nginx.org/download/nginx-1.26.1.tar.gz git clone http…...

单片机课设-基于单片机的电子时钟设计(仿真+代码+报告)
基于单片机的电子时钟设计 前言一、课设任务是什么?二、系统总体方案硬件设计2.1 系统硬件总体设计2.2 键盘电路设计2.3 DS1302实时时钟芯片电路设计2.4 复位电路2.5 LCD电路设计 三、软件设计3.1 主程序流程图3.2 主要程序设计代码3.3 修改时间函数3.4 扫描键盘函数 四、仿真…...

.net 6 api 修改URL为小写
我们创建的api项目,url是[Route(“[controller]”)],类似这样子定义的。我们的controller命名是大写字母开头的,显示在url很明显不是很好看(url不区分大小写)。转换方式: var builder WebApplication.Crea…...
Windows电脑部署Jellyfin服务端并进行远程访问配置详细教程
文章目录 前言1. Jellyfin服务网站搭建1.1 Jellyfin下载和安装1.2 Jellyfin网页测试 2.本地网页发布2.1 cpolar的安装和注册2.2 Cpolar云端设置2.3 Cpolar本地设置 3.公网访问测试4. 结语 前言 本文主要分享如何使用Windows电脑本地部署Jellyfin影音服务并结合cpolar内网穿透工…...

rsync同步目录脚本
假设有两台服务器的示例 IP 地址为: Server A: 192.168.1.100Server B: 192.168.1.200 现在来解释如何使用这个脚本进行服务器之间文件夹内容的同步,保留路径和服务器信息的抽象化。 1. 脚本文件位置和权限 假设脚本文件位于 /root/script.sh&#x…...

LeetCode 6. Z 字形变换
LeetCode 6. Z 字形变换 将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。 比如输入字符串为 “PAYPALISHIRING” 行数为 3 时,排列如下: 之后,你的输出需要从左往右逐行读取,产生…...

RTC实时时钟
一、Unix时间戳 1、Unix 时间戳 (1)Unix 时间戳(Unix Timestamp)定义为从UTC/GMT的1970年1月1日0时0分0秒开始所经过的秒数,不考虑闰秒 (2)时间戳存储在一个秒计数器中,秒计数器为…...
)
WHAT - React 学习系列(一)
官方文档 If you have a lot of HTML to port to JSX, you can use an online converter. You’ll get two things from useState: the current state (count), and the function that lets you update it (setCount). To “remember” things, components use state.To mak…...
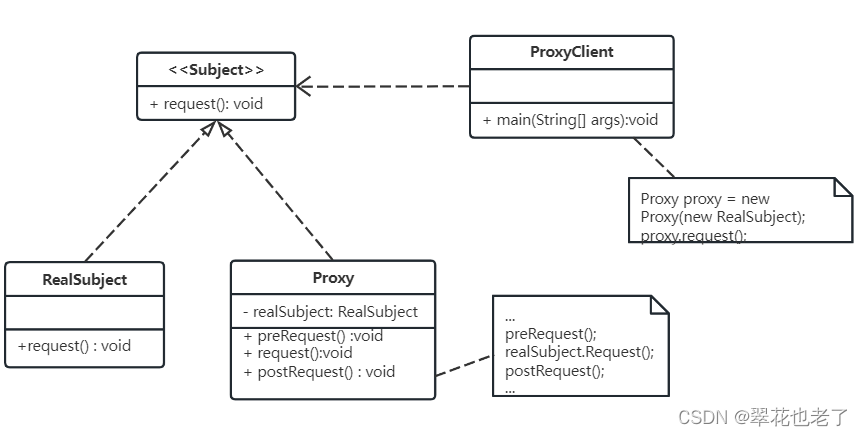
代理模式(静态代理/动态代理)
代理模式(Proxy Pattern) 一 定义 为其他对象提供一种代理,以控制对这个对象的访问。 代理对象在客户端和目标对象之间起到了中介作用,起到保护或增强目标对象的作用。 属于结构型设计模式。 代理模式分为静态代理和动态代理。…...
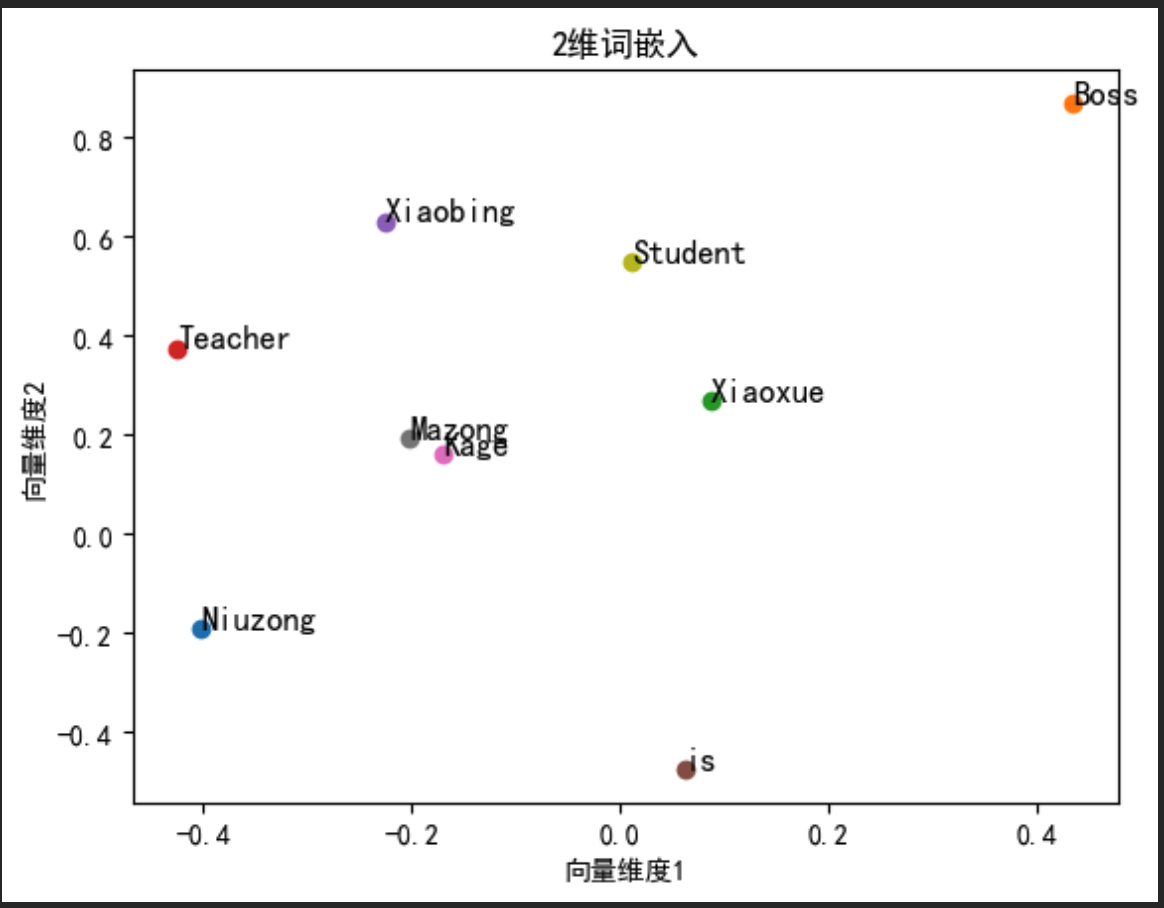
Word2Vec基本实践
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目…...
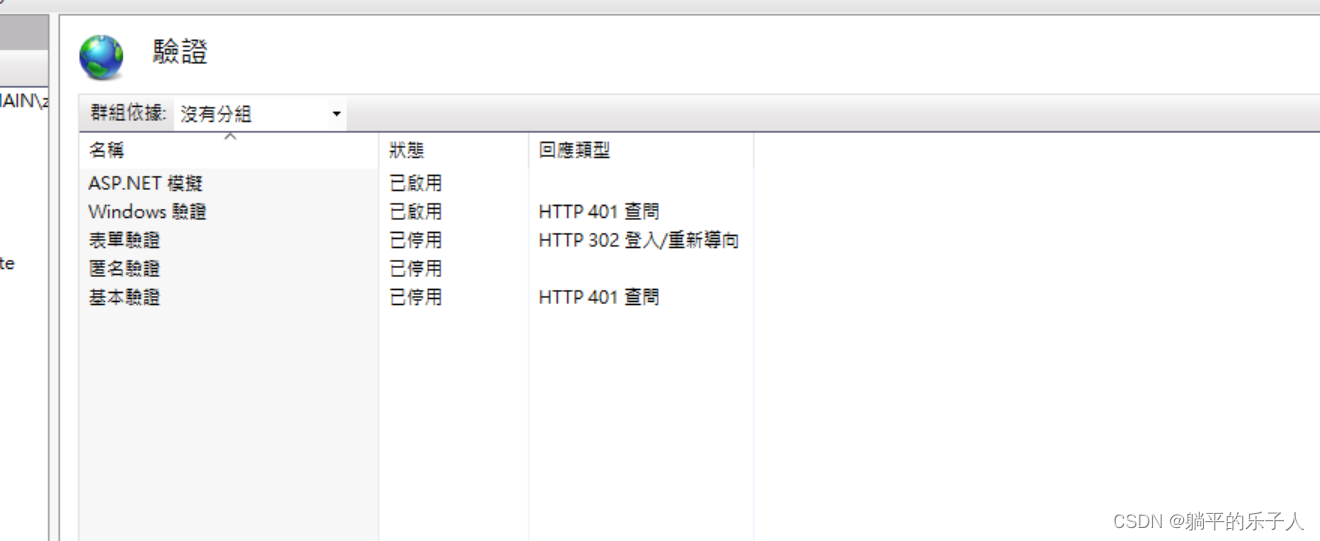
IIS配置網站登錄驗證,禁止匿名登陸
需要維護一個以前的舊系統,這個系統在內網運行,需要抓取電腦的登陸賬號,作為權限管理的一部分因此需要在IIS配置一下...

抖音矩阵系统搭建,AI剪辑短视频,一键管理矩阵账号
目录 前言: 一、抖音矩阵系统有哪些功能? 1.AI智能文案 2.多平台账号授权 3.多种剪辑模式 4. 矩阵一键发布,智能发布 5.抖音爆店码功能 6.私信实时互动 7.去水印及外链 二、抖音矩阵系统可以解决哪些问题? 总结ÿ…...

山东大学软件学院创新项目实训开发日志——收尾篇
山东大学软件学院创新项目实训开发日志——收尾篇 项目名称:ModuFusion Visionary:实现跨模态文本与视觉的相关推荐 -------项目目标: 本项目旨在开发一款跨模态交互式应用,用户可以上传图片或视频,并使用文本、点、…...

vue2.7支持组合式API,但是对应的vue-router3并不支持useRoute、useRouter。
最近在做一个项目,因为目标用户浏览器版本并不确定,可能会有较旧版本,于是采用vue2.7而不是vue3,最近一年多使用vue3开发的项目都碰到了很多chrome 63-73版本,而对应UI 库 element plus又问题很多。 为了不碰到这些问…...
摊位纠纷演变肢体冲突,倒赔了500:残疾夫妇与摊主谁之过?
在一个小商贩密集的街区,一起由摊位纠纷引发的肢体冲突事件在当地社区和网络上引起了热议。涉事双方为一名摊主和一对残疾夫妇,他们的争执源自对一个摊位的使用权。本是口头上的争吵,却由于双方情绪激动,迅速升级为肢体冲突&#…...
深入理解和实现Windows进程间通信(消息队列)
常见的进程间通信方法 常见的进程间通信方法有: 管道(Pipe)消息队列共享内存信号量套接字 下面,我们将详细介绍消息队列的原理以及具体实现。 什么是消息队列? Windows操作系统使用消息机制来促进应用程序与操作系…...

Web网页前端教程免费:引领您踏入编程的奇幻世界
Web网页前端教程免费:引领您踏入编程的奇幻世界 在当今数字化时代,Web前端技术已成为互联网发展的重要驱动力。想要踏入这一领域,掌握相关技能,却苦于找不到合适的教程?别担心,本文将为您带来一份免费的We…...

北斗短报文终端在应急消防通信场景中的应用
在应对自然灾害和紧急情况时,北斗三号短报文终端以其全球覆盖、实时通信和精准定位的能力,成为应急消防通信的得力助手。它不仅能够在地面通信中断的极端条件下保障信息传递的畅通,还能提供精准的位置信息,为救援行动提供有力支持…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
