【数学建模】——【新手小白到国奖选手】——【学习路线】

专栏:数学建模学习笔记
目录
编辑
第一阶段:基础知识和工具
1.Python基础
1.学习内容
1.基本语法
2.函数和模块
3.面向对象编程
4.文件操作
2.推荐资源
书籍:
在线课程:
在线教程:
2.数学基础
1.学习内容
1.高等数学
2.线性代数
3.概率论与数理统计
2.推荐教材
2.常用Python库
1.学习内容
1.NumPy
2.Pandas
3.Matplotlib和Seaborn
2.推荐资源
书籍:
在线课程:
在线教程:
第二阶段:数学建模基础
数学建模入门
学习内容
数学建模概念
经典数学模型
推荐书籍和课程
书籍:
在线课程:
2.编程实现
学习内容
实践练习
第三阶段:进阶学习
优化方法
学习内容
推荐书籍
机器学习基础
学习内容
推荐资源
书籍:
在线课程:
项目实践
实践内容
实践平台
第四阶段:专业提升
高级算法和模型
学习内容
推荐资源
科学计算和仿真
学习内容
推荐书籍
学术研究
学习内容
推荐资源
实践经验和竞赛
竞赛内容
竞赛准备
总结
第一阶段:基础知识和工具
第二阶段:数学建模基础
第三阶段:进阶学习
第四阶段:专业提升
实践经验和竞赛
第一阶段:基础知识和工具
1.Python基础
掌握Python基础是进行数学建模的第一步。Python的易用性和丰富的库使其成为数据科学和数学建模的理想选择。
1.学习内容
1.基本语法
变量和数据类型:学习如何声明变量以及不同的数据类型(整数int,浮点数float,字符串str,列表list,元组tuple,字典dict,集合set)。
a = 10 # 整数
b = 3.14 # 浮点数
c = "Hello, World!" # 字符串
d = [1, 2, 3] # 列表
e = (1, 2, 3) # 元组
f = {"name": "Alice", "age": 25} # 字典
g = {1, 2, 3} # 集合
运算符:熟悉算术运算符(+,-,*,/),比较运算符(==,!=,>,<,>=,<=),逻辑运算符(and,or,not)。
# 算术运算符
print(a + b) # 13.14
print(a * b) # 31.4# 比较运算符
print(a == b) # False
print(a > b) # True# 逻辑运算符
print(a > 5 and b < 5) # True
print(not (a > 5)) # False
控制结构:掌握条件语句(if,elif,else)和循环语句(for,while)。
if a > b:print("a is greater than b")
else:print("a is not greater than b")for i in range(5):print(i)count = 0
while count < 5:print(count)count += 1
2.函数和模块
-
自定义函数:学会定义函数,传递参数和返回值。
def add(x, y):return x + yresult = add(10, 5) print(result) # 15内置函数:使用Python提供的内置函数,如
len(),sum(),max(),min()等。my_list = [1, 2, 3, 4, 5] print(len(my_list)) # 5 print(sum(my_list)) # 15 print(max(my_list)) # 5 print(min(my_list)) # 1模块的导入和使用:学习如何导入和使用模块,例如
math模块。import math print(math.sqrt(16)) # 4.0 print(math.pi) # 3.1415926535897933.面向对象编程
-
类和对象:学习如何定义类和创建对象。
class Person:def __init__(self, name, age):self.name = nameself.age = agedef greet(self):print(f"Hello, my name is {self.name} and I am {self.age} years old.")person = Person("Alice", 25) person.greet() # Hello, my name is Alice and I am 25 years old.继承和多态:理解类的继承机制和多态性。
class Animal:def __init__(self, name):self.name = namedef speak(self):passclass Dog(Animal):def speak(self):return "Woof"class Cat(Animal):def speak(self):return "Meow"animals = [Dog("Fido"), Cat("Whiskers")] for animal in animals:print(f"{animal.name} says {animal.speak()}") # Fido says Woof # Whiskers says Meow4.文件操作
-
文件的读写:学习如何读取和写入文本文件及CSV文件。
# 写入文件 with open("example.txt", "w") as file:file.write("Hello, World!")# 读取文件 with open("example.txt", "r") as file:content = file.read()print(content) # Hello, World!异常处理:掌握如何处理程序运行中的异常。
try:result = 10 / 0 except ZeroDivisionError:print("Cannot divide by zero") finally:print("Execution finished")2.推荐资源
-
书籍:
- 《Python编程:从入门到实践》:这本书由Eric Matthes编写,覆盖了Python编程的基础知识和实际项目,非常适合初学者。
- 《Python基础教程》:Mark Lutz编写的这本书详细介绍了Python的核心概念和编程实践。
-
在线课程:
- Codecademy的Python课程:提供交互式的编程练习,适合零基础入门。
- Coursera上的“Python for Everybody”系列课程:由密歇根大学提供,讲师Charles Severance详细讲解了Python基础。
-
在线教程:
- W3Schools的Python教程:提供简洁明了的Python语法和示例。
- GeeksforGeeks的Python教程:涵盖了从基础到高级的Python编程知识,适合系统学习。
2.数学基础
扎实的数学基础是进行数学建模的基石。以下是需要掌握的数学知识:
1.学习内容
1.高等数学
微积分:
微分:学习导数的定义、求导法则、函数的微分应用(如极值问题、最速下降法)。
import sympy as sp
x = sp.symbols('x')
f = x**3 + 2*x**2 + x
f_prime = sp.diff(f, x)
print(f_prime) # 3*x**2 + 4*x + 1
积分:理解定积分和不定积分的概念,以及如何进行积分运算。
F = sp.integrate(f, x)
print(F) # x**4/4 + 2*x**3/3 + x**2/2
函数和极限:
- 学习函数的定义和各种类型的函数(如多项式函数、指数函数、对数函数)。
- 理解极限的概念及其在分析中的应用
limit_value = sp.limit(f/x, x, sp.oo) print(limit_value) # 1函数和极限:
- 学习函数的定义和各种类型的函数(如多项式函数、指数函数、对数函数)。
- 理解极限的概念及其在分析中的应用。
limit_value = sp.limit(f/x, x, sp.oo) print(limit_value) # 1数列和级数:
- 学习数列的定义及其基本性质。
- 理解级数的概念,特别是收敛和发散。
n = sp.symbols('n') series_sum = sp.Sum(1/n**2, (n, 1, sp.oo)).doit() print(series_sum) # pi**2/62.线性代数
b = sp.Matrix([5, 11]) x = A.LUsolve(b) print(x) # Matrix([[1], [2]])
矩阵和向量:
- 学习矩阵和向量的基本运算(如加法、乘法、转置)。
- 理解矩阵的逆、行列式和特征值。
A = sp.Matrix([[1, 2], [3, 4]]) A_inv = A.inv() print(A_inv) # Matrix([[-2, 1], [3/2, -1/2]])线性方程组:
- 学习如何使用矩阵求解线性方程组。
b = sp.Matrix([5, 11]) x = A.LUsolve(b) print(x) # Matrix([[1], [2]])特征值和特征向量:
- 理解特征值和特征向量的定义及其计算方法。
eigenvals = A.eigenvals() eigenvects = A.eigenvects() print(eigenvals) # {5: 1, -1: 1} print(eigenvects)3.概率论与数理统计
概率基础:
学习概率的基本概念和规则(如概率分布、条件概率、独立性)
from sympy import FiniteSet
outcomes = FiniteSet(1, 2, 3, 4, 5, 6)
event = FiniteSet(2, 4, 6)
probability = len(event) / len(outcomes)
print(probability) # 0.5
随机变量和分布:
理解随机变量的概念和常见的概率分布(如正态分布、二项分布)。
from scipy.stats import norm
mean, std_dev = 0, 1
probability = norm.cdf(1) - norm.cdf(-1)
print(probability) # 0.6826894921370859
统计推断:
- 学习假设检验、置信区间等统计推断方法。
import numpy as np data = np.random.normal(mean, std_dev, 100) conf_interval = np.percentile(data, [2.5, 97.5]) print(conf_interval)2.推荐教材
- 《高等数学》:教材详细介绍了微积分和高等数学的基本概念和应用。
- 《线性代数》:涵盖了矩阵、向量和线性方程组的基础知识。
- 《概率论与数理统计》:提供了概率论和统计推断的基本理论和应用。
2.常用Python库
熟练使用Python中的几个重要库可以大大简化数值计算、数据处理和可视化的过程。
1.学习内容
1.NumPy
-
数组和矩阵操作:
- 学习如何创建和操作NumPy数组和矩阵。
import numpy as np a = np.array([1, 2, 3]) b = np.array([[1, 2], [3, 4]]) print(a + 1) # [2 3 4] print(b.T) # [[1 3] [2 4]]数学函数和随机数生成:
- 使用NumPy进行常用的数学运算和生成随机数。
c = np.sin(a) d = np.random.normal(0, 1, 1000) print(c) print(d.mean(), d.std())线性代数运算:
- 进行矩阵乘法、求逆、特征值计算等线性代数运算。
e = np.linalg.inv(b) f = np.dot(b, e) print(f) # [[1 0] [0 1]]2.Pandas
-
数据结构:
- 学习Pandas中的基本数据结构:Series和DataFrame。
import pandas as pd s = pd.Series([1, 2, 3]) df = pd.DataFrame({'A': [1, 2, 3], 'B': [4, 5, 6]}) print(s) print(df)数据导入和导出:
- 学习如何读取和写入CSV文件及其他格式的数据文件。
df.to_csv('example.csv', index=False) df_read = pd.read_csv('example.csv') print(df_read)数据清洗和处理:
- 使用Pandas进行数据清洗和处理操作,如缺失值处理、数据筛选和排序。
df['C'] = df['A'] + df['B'] df_cleaned = df.dropna() df_sorted = df.sort_values(by='C') print(df_cleaned) print(df_sorted)3.Matplotlib和Seaborn
-
基本图形绘制:
- 使用Matplotlib绘制基本图形,如折线图、柱状图、散点图。
import matplotlib.pyplot as plt plt.plot(a) plt.bar(range(len(a)), a) plt.scatter(a, c) plt.show()高级绘图:
- 使用Seaborn进行高级数据可视化,如热力图、分布图。
import seaborn as sns sns.heatmap(df.corr(), annot=True) sns.distplot(d) plt.show()2.推荐资源
-
书籍:
- 《Python数据分析》:Wes McKinney编写,详细介绍了Pandas的使用。
- 《利用Python进行数据分析》:Wes McKinney编写,涵盖了Pandas和NumPy的基础和进阶使用。
-
在线课程:
- Coursera的“Data Analysis with Python”课程:提供全面的数据分析教程。
- edX的“Analyzing Data with Python”课程:深入讲解数据分析的各个方面。
-
在线教程:
- 官方文档:NumPy、Pandas、Matplotlib和Seaborn的官方文档是学习这些库的最佳资源。
- GeeksforGeeks:提供了从基础到高级的详细教程。
- 使用Matplotlib绘制基本图形,如折线图、柱状图、散点图。
- 学习Pandas中的基本数据结构:Series和DataFrame。
- 学习如何创建和操作NumPy数组和矩阵。
第二阶段:数学建模基础
数学建模入门
在具备了基本的编程和数学知识后,可以开始接触数学建模的基本概念和方法。
学习内容
数学建模概念
什么是数学建模:
数学建模是利用数学工具和方法对实际问题进行描述、分析和求解的过程。
数学模型通过对实际问题进行抽象和简化,建立数学表达式或方程来描述问题。
数学建模的基本步骤:
- 问题描述:明确要解决的问题,收集相关信息和数据。
- 假设条件:对实际问题进行合理的简化和假设,以便建立模型。
- 模型构建:根据假设条件,建立数学模型,如方程、函数、关系式等。
- 求解模型:利用数学方法或计算工具求解模型,得到结果。
- 模型验证:将模型结果与实际情况进行比较,验证模型的有效性。
- 模型改进:根据验证结果,修正假设和模型,进一步优化模型。
经典数学模型
优化问题:
线性规划:求解线性约束条件下的最优化问题。
from scipy.optimize import linprog
c = [-1, -2]
A = [[2, 1], [1, 2]]
b = [20, 20]
x0_bounds = (0, None)
x1_bounds = (0, None)
result = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds])
print(result)
整数规划:线性规划的整数解形式,常用于资源分配和调度问题。
from scipy.optimize import linprog
c = [-1, -2]
A = [[2, 1], [1, 2]]
b = [20, 20]
x0_bounds = (0, None)
x1_bounds = (0, None)
result = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='simplex')
print(result)
回归分析:
线性回归:用于预测连续型变量,假设因变量与自变量之间存在线性关系。
import numpy as np
from sklearn.linear_model import LinearRegression
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([1, 3, 5, 7, 9])
model = LinearRegression().fit(X, y)
predictions = model.predict(X)
print(predictions)
多项式回归:适用于因变量与自变量之间存在非线性关系的情况。
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
model_poly = LinearRegression().fit(X_poly, y)
predictions_poly = model_poly.predict(X_poly)
print(predictions_poly)
时间序列分析:
- ARIMA模型:用于预测时间序列数据,结合了自回归、差分和移动平均成分
from statsmodels.tsa.arima.model import ARIMA model_arima = ARIMA(y, order=(1, 1, 1)) result_arima = model_arima.fit() predictions_arima = result_arima.forecast(steps=5) print(predictions_arima)推荐书籍和课程
-
书籍:
- 《数学建模(原书第5版)》:Steven C. Chapra和Raymond P. Canale编写,详细介绍了数学建模的基本原理和应用。
- 《运筹学》:涵盖了线性规划、整数规划等优化方法。
-
在线课程:
- Coursera的“Mathematical Modeling Basics”课程:由荷兰代尔夫特理工大学提供,介绍了数学建模的基础知识。
- edX的“Introduction to Mathematical Modeling”课程:由麻省理工学院提供,详细讲解了数学建模的基本方法。
2.编程实现
用Python实现简单的数学模型是从理论到实践的重要一步。
学习内容
线性回归模型
数据预处理:
对数据进行预处理,包括数据清洗、特征选择和数据标准化。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
模型训练和预测:
使用线性回归模型进行训练和预测。
model = LinearRegression().fit(X_scaled, y)
predictions = model.predict(X_scaled)
模型评估:
使用均方误差(MSE)、决定系数(R^2)等指标评估模型性能。
from sklearn.metrics import mean_squared_error, r2_score
mse = mean_squared_error(y, predictions)
r2 = r2_score(y, predictions)
print(f"MSE: {mse}, R^2: {r2}")
多项式回归模型
多项式特征生成:
使用PolynomialFeatures生成多项式特征。
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
模型训练和预测:
- 使用多项式回归模型进行训练和预测。
model_poly = LinearRegression().fit(X_poly, y) predictions_poly = model_poly.predict(X_poly)模型评估和选择:
- 比较多项式回归模型与线性回归模型的性能,选择最佳模型。
mse_poly = mean_squared_error(y, predictions_poly) r2_poly = r2_score(y, predictions_poly) print(f"Polynomial Regression - MSE: {mse_poly}, R^2: {r2_poly}")实践练习
利用Python库实现上述模型:
使用scikit-learn库实现线性回归和多项式回归模型,掌握从数据导入、清洗、建模到结果分析的完整流程。
第三阶段:进阶学习

优化方法
优化方法是数学建模的重要工具,涉及如何找到最优解或最优策略。
学习内容
线性规划
-
线性规划的基本概念和标准形式:
- 理解线性规划问题的定义、目标函数、约束条件。
- 学习如何将实际问题转化为线性规划问题。
-
单纯形法和对偶理论:
- 学习单纯形法的基本原理和算法步骤。
- 理解对偶理论及其在求解线性规划问题中的应用。
-
非线性规划
-
非线性规划的基本概念:
- 理解非线性规划问题的定义、目标函数、约束条件。
- 学习常见的非线性规划问题及其应用场景。
-
常用算法:
-
梯度下降法:用于求解无约束优化问题,通过迭代逼近最优解。
import numpy as np def gradient_descent(f, grad_f, x0, learning_rate, max_iter):x = x0for _ in range(max_iter):x = x - learning_rate * grad_f(x)return x牛顿法:用于求解无约束优化问题,通过二阶导数加速收敛。
def newton_method(f, grad_f, hessian_f, x0, max_iter):x = x0for _ in range(max_iter):H_inv = np.linalg.inv(hessian_f(x))x = x - H_inv @ grad_f(x)return x推荐书籍
- 《运筹学》:详细介绍了线性规划、非线性规划等优化方法及其应用。
- 《线性规划与网络流》:深入讲解了线性规划和网络流问题的理论和算法。
-
-
机器学习基础
机器学习是数学建模的一个重要方向,尤其在数据驱动的建模中,机器学习方法发挥了巨大作用。
学习内容
监督学习
回归算法:
线性回归:学习线性回归的原理和实现方法。
from sklearn.linear_model import LinearRegression
model = LinearRegression().fit(X, y)
predictions = model.predict(X)
岭回归:学习如何通过正则化防止过拟合。
from sklearn.linear_model import Ridge
model_ridge = Ridge(alpha=1.0).fit(X, y)
predictions_ridge = model_ridge.predict(X)
Lasso回归:学习Lasso回归的原理和实现方法。
from sklearn.linear_model import Lasso
model_lasso = Lasso(alpha=0.1).fit(X, y)
predictions_lasso = model_lasso.predict(X)
分类算法:
-
决策树:学习决策树算法的原理和实现方法。
from sklearn.tree import DecisionTreeClassifier model_tree = DecisionTreeClassifier().fit(X, y) predictions_tree = model_tree.predict(X)支持向量机:学习SVM算法的原理和实现方法。
from sklearn.svm import SVC model_svm = SVC(kernel='linear').fit(X, y) predictions_svm = model_svm.predict(X)K近邻:学习KNN算法的原理和实现方法。
from sklearn.neighbors import KNeighborsClassifier model_knn = KNeighborsClassifier(n_neighbors=3).fit(X, y) predictions_knn = model_knn.predict(X)无监督学习
-
聚类算法:
-
K均值聚类:学习K-means算法的原理和实现方法。
from sklearn.cluster import KMeans model_kmeans = KMeans(n_clusters=3).fit(X) predictions_kmeans = model_kmeans.predict(X)层次聚类:学习层次聚类算法的原理和实现方法。
from scipy.cluster.hierarchy import dendrogram, linkage Z = linkage(X, 'ward') dendrogram(Z) plt.show()降维方法:
-
主成分分析(PCA):学习PCA的原理和实现方法。
from sklearn.decomposition import PCA model_pca = PCA(n_components=2).fit(X) X_pca = model_pca.transform(X)t-SNE:学习t-SNE的原理和实现方法。
from sklearn.manifold import TSNE X_tsne = TSNE(n_components=2).fit_transform(X)推荐资源
-
书籍:
- 《统计学习方法》:李航编写,系统介绍了机器学习的基本算法和理论。
- 《机器学习实战》:Peter Harrington编写,提供了丰富的实际案例和代码示例。
-
在线课程:
- Coursera的“Machine Learning”课程:由斯坦福大学提供,Andrew Ng教授讲解,覆盖了机器学习的核心内容。
- Udacity的“Intro to Machine Learning”课程:提供了丰富的实践练习和项目。
-
项目实践
项目实践是将所学知识应用到实际问题中的重要环节。通过项目可以锻炼解决实际问题的能力。
实践内容
-
选择实际问题
- 预测股市价格:利用历史数据构建模型,预测未来的股市价格。
- 优化生产调度:利用线性规划和整数规划优化生产计划,提高效率。
- 分析社交网络:利用图论和机器学习分析社交网络中的用户行为和关系。
-
项目流程
- 问题描述和数据收集:明确问题和目标,收集相关数据。
- 数据预处理和特征工程:对数据进行清洗、处理和特征提取。
- 模型选择和训练:选择合适的模型,进行训练和调参。
- 模型评估和优化:使用各种指标评估模型性能,并进行优化。
- 结果分析和报告撰写:分析模型结果,撰写详细的项目报告。
-
实践平台
- Kaggle:数据科学竞赛平台,提供丰富的数据集和竞赛题目。
- 天池:阿里云的人工智能竞赛平台,有很多有趣的竞赛和项目。
-
第四阶段:专业提升
-
高级算法和模型
掌握高级算法和模型是迈向专家级别的必经之路。这些方法通常应用于复杂问题和前沿研究。
学习内容
-
深度学习
-
深度神经网络(DNN):
- 学习DNN的基本结构和原理。
- 了解常见的激活函数(如ReLU、Sigmoid、Tanh)和损失函数。
from keras.models import Sequential from keras.layers import Dense model_dnn = Sequential() model_dnn.add(Dense(units=64, activation='relu', input_dim=100)) model_dnn.add(Dense(units=10, activation='softmax')) model_dnn.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])卷积神经网络(CNN):
- 学习CNN的基本结构和原理,了解卷积层、池化层和全连接层。
from keras.layers import Conv2D, MaxPooling2D, Flatten model_cnn = Sequential() model_cnn.add(Conv2D(32, (3, 3), activation='relu', input_shape=(64, 64, 3))) model_cnn.add(MaxPooling2D(pool_size=(2, 2))) model_cnn.add(Flatten()) model_cnn.add(Dense(units=128, activation='relu')) model_cnn.add(Dense(units=1, activation='sigmoid')) model_cnn.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])循环神经网络(RNN):
- 学习RNN的基本结构和原理,了解LSTM和GRU等变体。
from keras.layers import SimpleRNN, LSTM model_rnn = Sequential() model_rnn.add(LSTM(units=50, return_sequences=True, input_shape=(10, 1))) model_rnn.add(LSTM(units=50)) model_rnn.add(Dense(units=1)) model_rnn.compile(optimizer='adam', loss='mean_squared_error')强化学习
-
基本概念:
- 理解强化学习的基本概念,如马尔可夫决策过程(MDP)、状态、动作、奖励、价值函数。
- 学习强化学习的框架和工作流程。
-
算法:
-
Q-learning:学习Q-learning算法的原理和实现方法。
import numpy as np def q_learning(env, num_episodes, alpha, gamma, epsilon):Q = np.zeros((env.observation_space.n, env.action_space.n))for i in range(num_episodes):state = env.reset()done = Falsewhile not done:if np.random.rand() < epsilon:action = env.action_space.sample()else:action = np.argmax(Q[state, :])next_state, reward, done, _ = env.step(action)Q[state, action] = Q[state, action] + alpha * (reward + gamma * np.max(Q[next_state, :]) - Q[state, action])state = next_statereturn Q深度Q网络(DQN):学习DQN的原理和实现方法,结合深度学习进行策略优化。
import keras from keras.models import Sequential from keras.layers import Dense model_dqn = Sequential() model_dqn.add(Dense(units=24, activation='relu', input_dim=env.observation_space.shape[0])) model_dqn.add(Dense(units=24, activation='relu')) model_dqn.add(Dense(units=env.action_space.n, activation='linear')) model_dqn.compile(loss='mse', optimizer=keras.optimizers.Adam(lr=0.001))推荐资源
- 书籍:
- 《深度学习(Goodfellow)》:Ian Goodfellow编写,全面介绍了深度学习的基础理论和实践方法。
- 《强化学习(Sutton)》:Richard S. Sutton和Andrew G. Barto编写,详细讲解了强化学习的基本原理和算法。
-
-
科学计算和仿真
科学计算和仿真是解决复杂问题的重要工具,常用于物理、工程和经济等领域。
学习内容
-
蒙特卡洛仿真
- 基本原理:理解蒙特卡洛仿真的基本思想,通过随机数生成和概率统计模拟复杂系统
import numpy as np def monte_carlo_simulation(num_simulations, num_steps):results = []for _ in range(num_simulations):position = 0for _ in range(num_steps):position += np.random.choice([-1, 1])results.append(position)return np.mean(results), np.std(results) mean, std = monte_carlo_simulation(1000, 100) print(mean, std)元胞自动机
- 基本原理:学习元胞自动机的定义和基本规则,理解其在复杂系统建模中的应用。
import numpy as np def game_of_life(initial_state, num_generations):state = np.copy(initial_state)for _ in range(num_generations):new_state = np.copy(state)for i in range(1, state.shape[0] - 1):for j in range(1, state.shape[1] - 1):num_neighbors = np.sum(state[i-1:i+2, j-1:j+2]) - state[i, j]if state[i, j] == 1 and (num_neighbors < 2 or num_neighbors > 3):new_state[i, j] = 0elif state[i, j] == 0 and num_neighbors == 3:new_state[i, j] = 1state = new_statereturn state数值方法
- 微分方程数值解:学习常微分方程和偏微分方程的数值解法,如欧拉法、龙格-库塔法。
from scipy.integrate import odeint def model(y, t):dydt = -0.5 * yreturn dydt y0 = 5 t = np.linspace(0, 10, 100) y = odeint(model, y0, t) plt.plot(t, y) plt.xlabel('time') plt.ylabel('y(t)') plt.show()推荐书籍
- 《科学计算与仿真》:介绍了科学计算的基本方法和仿真技术。
- 《数值分析》:详细讲解了数值方法及其在科学计算中的应用。
- 基本原理:理解蒙特卡洛仿真的基本思想,通过随机数生成和概率统计模拟复杂系统
学术研究
学术研究是深入理解数学建模和优化方法的重要途径,通过阅读和撰写学术论文可以了解领域的最新进展。
学习内容
-
阅读学术论文
- 选择合适的论文:在Google Scholar、arXiv等平台上查找相关领域的学术论文。
- 批判性阅读:阅读论文时,重点关注问题的提出、方法的应用、结果的分析和结论的提炼。
-
撰写学术论文
- 选题和文献综述:选择研究方向,进行相关文献的综述。
- 研究方法和实验设计:详细描述研究方法和实验设计,包括数据收集、模型构建和结果分析。
- 论文写作和发表:按照学术规范撰写论文,选择合适的期刊或会议进行投稿。
推荐资源
- Google Scholar:学术搜索引擎,提供丰富的学术论文资源。
- arXiv:预印本论文存档,涵盖了物理、数学、计算机科学等多个领域。
实践经验和竞赛
多参加数学建模竞赛,如全国大学生数学建模竞赛、美赛等,通过竞赛积累经验,提升实战能力。
竞赛内容
-
全国大学生数学建模竞赛
- 竞赛形式:每年9月举行,持续3天,参赛队伍需要在规定时间内完成数学建模论文。
- 竞赛题目:题目涉及实际问题,要求参赛队伍运用数学建模方法进行分析和求解。
-
美赛(Mathematical Contest in Modeling, MCM)
- 竞赛形式:每年2月举行,持续4天,参赛队伍需要在规定时间内完成数学建模论文。
- 竞赛题目:题目涉及实际问题,要求参赛队伍运用数学建模方法进行分析和求解。
竞赛准备
- 团队组建:选择合适的队友,分工明确,充分发挥团队优势。
- 题目选择:根据自身优势和兴趣选择竞赛题目,合理分配时间和任务。
- 文献查找:利用各种资源查找相关文献,了解问题背景和现有研究成果。
- 模型构建和求解:运用所学知识构建模型,利用编程工具进行求解和验证。
- 论文撰写和修改:按照竞赛要求撰写论文,重点突出模型的创新点和实际应用价值,反复修改和润色。
总结
通过详细的学习和实践路线,初学者可以逐步提升Python数学建模的能力,最终在相关竞赛中取得优异成绩。整个过程可以分为以下四个阶段:
第一阶段:基础知识和工具
- Python基础:掌握Python的基本语法、数据类型、控制结构、函数和模块、面向对象编程、文件操作等内容。推荐学习资源包括《Python编程:从入门到实践》和Codecademy的Python课程。
- 数学基础:复习高等数学、线性代数、概率论与数理统计等课程。推荐教材有《高等数学》、《线性代数》和《概率论与数理统计》。
- 常用Python库:熟练使用NumPy、Pandas、Matplotlib和Seaborn等库进行数值计算、数据处理和可视化。推荐学习资源包括《Python数据分析》和官方文档。
第二阶段:数学建模基础
- 数学建模入门:了解数学建模的基本概念和步骤,学习经典数学模型如优化问题(线性规划、整数规划)、回归分析(线性回归、多项式回归)和时间序列分析(ARIMA模型)。推荐书籍包括《数学建模(原书第5版)》和《运筹学》。
- 编程实现:用Python实现简单的数学模型,如线性回归和多项式回归。通过数据预处理、模型训练、预测和评估,掌握从理论到实践的完整流程。
第三阶段:进阶学习
- 优化方法:学习线性规划和非线性规划的基本概念和常用算法,如单纯形法、梯度下降法和牛顿法。推荐书籍有《运筹学》和《线性规划与网络流》。
- 机器学习基础:掌握监督学习和无监督学习的基本算法,如线性回归、决策树、支持向量机、K均值聚类和主成分分析。推荐学习资源包括《统计学习方法》和Coursera的“Machine Learning”课程。
- 项目实践:选择实际问题进行建模,通过项目锻炼解决实际问题的能力。推荐实践平台包括Kaggle和天池。
第四阶段:专业提升
- 高级算法和模型:学习深度学习(如DNN、CNN、RNN)和强化学习(如Q-learning、DQN)的原理和实现方法。推荐书籍有《深度学习(Goodfellow)》和《强化学习(Sutton)》。
- 科学计算和仿真:掌握蒙特卡洛仿真、元胞自动机和数值方法的基本原理和应用。推荐书籍有《科学计算与仿真》和《数值分析》。
- 学术研究:通过阅读和撰写学术论文,了解数学建模领域的最新进展和研究方向。推荐资源包括Google Scholar和arXiv。
实践经验和竞赛
多参加数学建模竞赛,如全国大学生数学建模竞赛和美赛,通过竞赛积累经验,提升实战能力。竞赛准备包括团队组建、题目选择、文献查找、模型构建和求解、论文撰写和修改等步骤。
通过系统的学习和实践,你可以逐步提升数学建模能力,最终在相关竞赛中取得优异成绩,实现从初学者到专家的飞跃。
相关文章:

【数学建模】——【新手小白到国奖选手】——【学习路线】
专栏:数学建模学习笔记 目录 编辑 第一阶段:基础知识和工具 1.Python基础 1.学习内容 1.基本语法 2.函数和模块 3.面向对象编程 4.文件操作 2.推荐资源 书籍: 在线课程: 在线教程: 2.数学基础 1.学习内…...
CSS文本超限后使用省略号代替
方案一: 只显示一行,超限后使用省略号代替 .detail {overflow: hidden;text-overflow: ellipsis;white-space: nowrap; }方案二: 显示多行,到最后一行还没有显示完,则最后一行多出来的部分使用省略号代替。 .detai…...

多线程下JVM内存模型 和 volatile关键字
1、线程的概念 线程(thread)是操作系统能够进行运算调度的最小单位。它被包含在进程之中,是进程中的实际运作单位。一条线程指的是进程中一个单一顺序的控制流,一个进程中可以并发多个线程,每条线程并行执行不同的任务…...

Uniapp实现页面滚动Tab吸顶,点击tab内容滚动到对应tab内容位置
思路:运用uniapp原生提供方法uni.createSelectorQuery()获取滚动对应节点的信息,即节点距离页面顶部的距离,再通过uniapp原生监听页面滚动事件onPageScroll,获取页面内容滚动的高度,二者相加即定位到对应节点的滚动距离…...

在Elasticsearch中-SpaceJam一个全文搜索的实例
在Elasticsearch中进行全文搜索通常涉及几个步骤:创建索引、定义映射、索引文档、执行搜索查询。下面我将通过一个名为"SpaceJam"的虚构实例来演示如何进行全文搜索。 ### 步骤 1: 创建索引 首先,我们需要创建一个索引。在这个例子中&#x…...
Microsoft Edge浏览器安装crx拓展插件教程
1、首先打开edge浏览器,点击顶部地址栏。 2、在地址栏中输入"edge://flags/#extensions-on-edge-urls"并按下回车。2、在地址栏中输入"edge://flags/#extensions-on-edge-urls"并按下回车。 3、进入后,将图示选项改为“已禁用”。 …...

陈晓婚前婚后大变样
陈晓婚前婚后大变样?陈妍希揭秘甜蜜与现实的碰撞在娱乐圈的星光璀璨中,有一对夫妻总是津津乐道,那就是陈晓和陈妍希。他们的爱情故事,从荧幕到现实,一直备受关注。然而,近日陈妍希在节目中透露,…...

Linux sudo -i取消密码的方法
直接修改 /etc/sudoers 文件来实现 sudo -i 无需密码的配置。以下是具体步骤: 步骤 打开终端并使用 visudo 命令编辑 /etc/sudoers 文件 使用 visudo 编辑 sudoers 文件是推荐的方法,因为它会在保存前进行语法检查,防止出现配置错误。 sudo …...
PMP考试多少分才算合格通过?
PMP是美国颁发的专业资格认证,其考试采用的是国外的评分体系。考试内容被划分为3大部分:人、过程和商业环境,每个部分所占的权重不同。考试形式为180个单选和多选题,其中有25题不计分。考试可能会抽到错误或未回答的题目,也可能抽到正确答题的题目。最终根据NBTA的4个等级进行综…...

原生js写数据自动纵向滚动,鼠标移入后停止滚动可手动滚动,鼠标移出转自动
<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>滚动页面</title><link rel"styleshee…...

板凳----Linux/Unix 系统编程手册 25章 进程的终止
25.1 进程的终止:_exit()和exit() 440 1. _exit(int status), status 定义了终止状态,父进程可调用 wait 获取。仅低8位可用,调用 _exit() 总是成功的。 2.程序一般不会调用 _exit(), 而是调用库函数 exit()。exit() …...
若依Ruoyi-vue和element admin的区别,该如何选择。
提到中后台的前端框架,每个人都能列举出很多,这其中提及率比较高的就是Ruoyi和element admin两款,很多小伙伴分不清二者,本文为大家详细讲解一下。 一、若依Ruoyi-vue是什么? 若依Ruoyi-Vue是一款基于 Vue.js 开发的…...
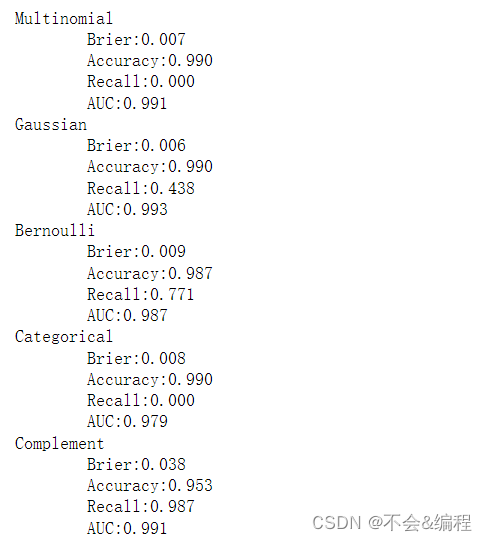
Sklearn之朴素贝叶斯应用
目录 sklearn中的贝叶斯分类器 前言 1 分类器介绍 2 高斯朴素贝叶斯GaussianNB 2.1 认识高斯朴素贝叶斯 2.2 高斯朴素贝叶斯建模案例 2.3 高斯朴素贝叶斯擅长的数据集 2.3.1 三种数据集介绍 2.3.2 构建三种数据 2.3.3 数据标准化 2.3.4 朴素贝叶斯处理数据 2.4 高斯…...
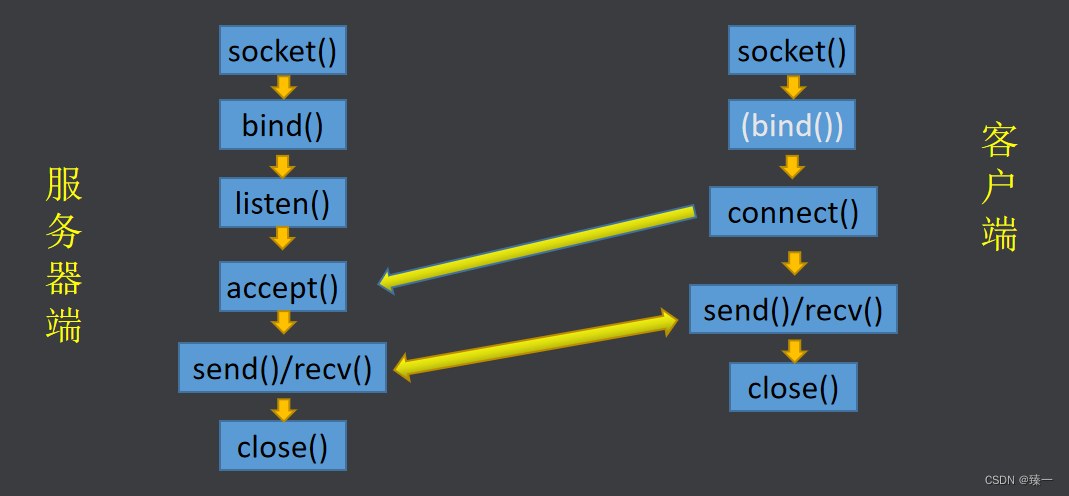
网络编程(二)TCP编程 TCP粘包问题
文章目录 一、TCP网络编程(一)流程(二)相关函数1. socket2. bind3. listen4. accept5. connect 二、收发函数(一)send函数(二)recv函数 三、TCP粘包问题(一)将…...
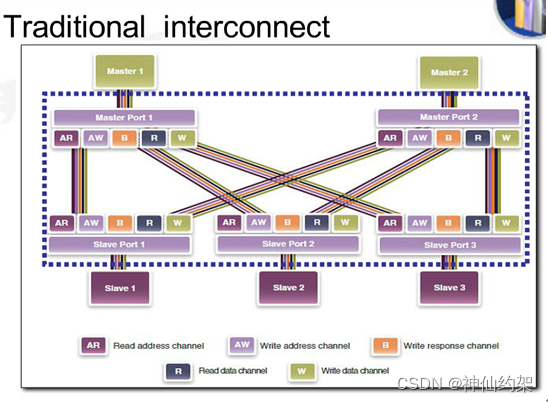
【总线】AXI总线:FPGA设计中的通信骨干
目录 AXI4:高性能地址映射通信的基石 AXI4-Lite:轻量级但功能强大的通信接口 AXI4-Stream:高速流数据传输的利器 结语:AXI总线在FPGA设计中的重要性 大家好,欢迎来到今天的总线学习时间!如果你对电子设计、特别是FPGA和SoC设计…...
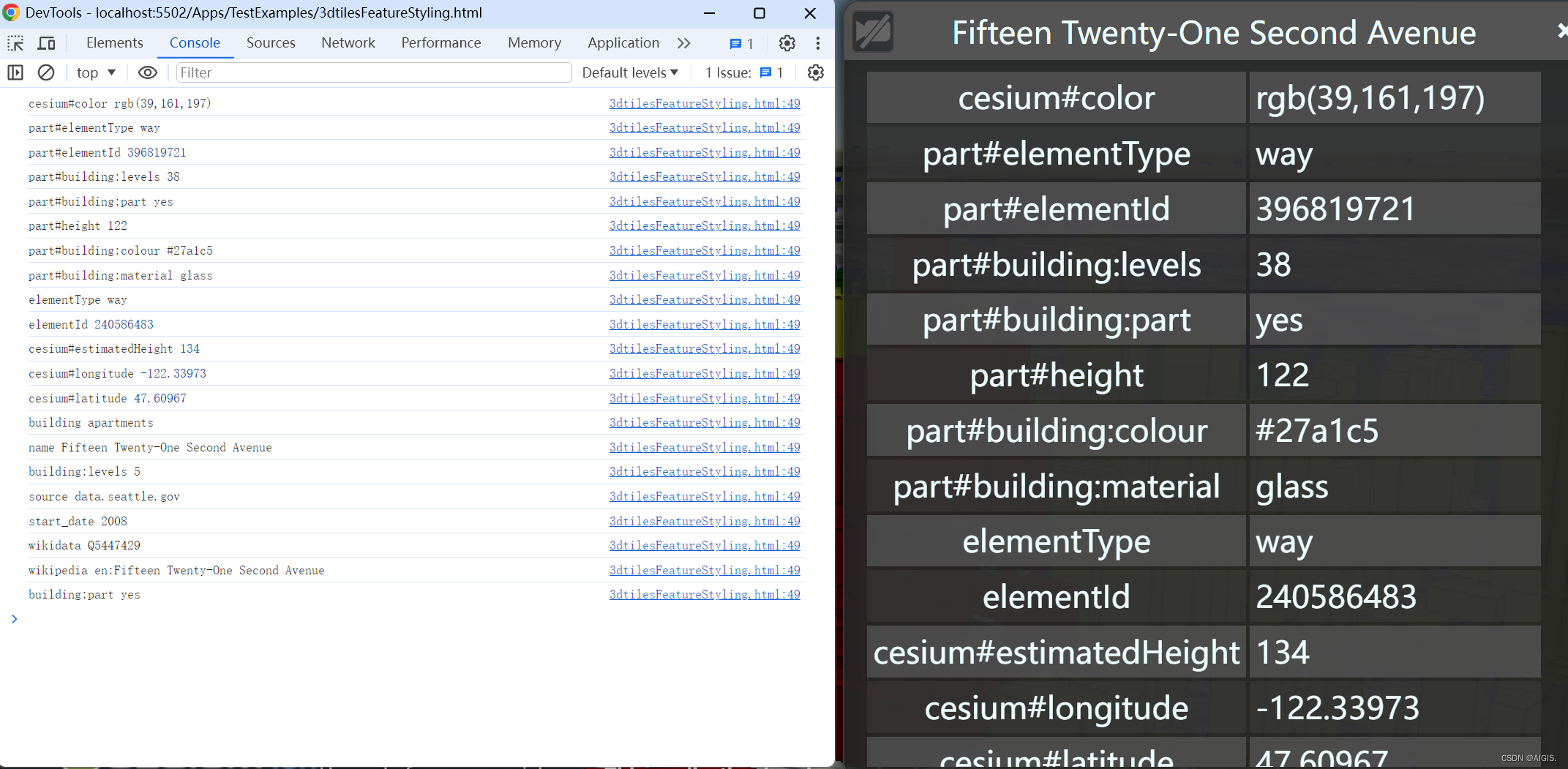
Cesium源码解析六(3dtiles属性获取、建筑物距离计算、建筑物着色及其原理分析)
快速导航 Cesium源码解析一(搭建开发环境) Cesium源码解析二(terrain文件的加载、解析与渲染全过程梳理) Cesium源码解析三(metadataAvailability的含义) Cesium源码解析四(metadata元数据拓展…...
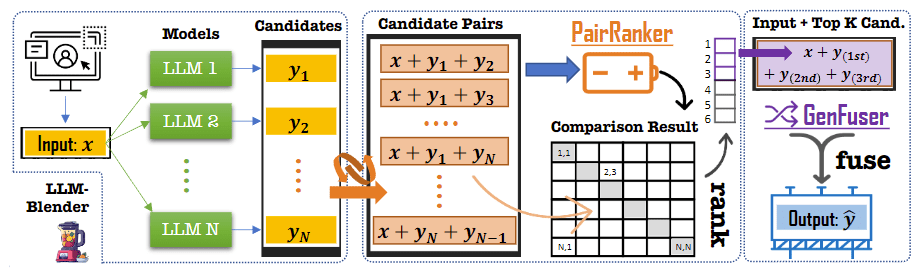
AI 情感聊天机器人之旅 —— 相关论文调研
开放域闲聊场景 Prompted LLMs as Chatbot Modules for Long Open-domain Conversation 发布日期:2023-05-01 简要介绍:作者提出了 MPC(模块化提示聊天机器人),这是一种无需微调即可创建高质量对话代理的新方法&…...
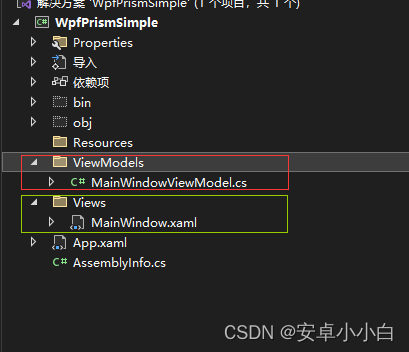
WPF Prism框架搭建
WPF Prism框架搭建 1.引入Prism框架 在Nuget包管理器中搜索Prism,并添加到项目中 2.在项目中使用prism框架 2.1 修改app.xaml 删除项目中自带的StartupUri 修改Application节点为prism:PrismApplication 引入prism命名空间 <prism:PrismApplication x:C…...
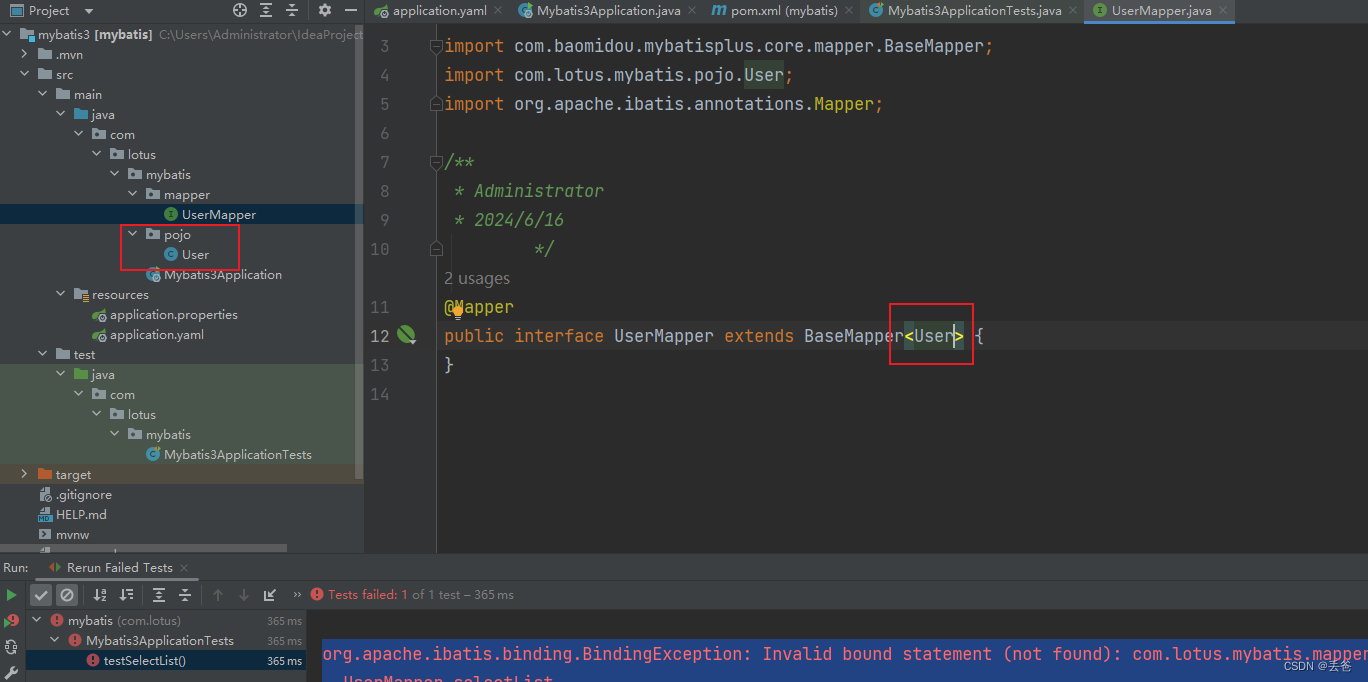
MyBatisplus使用报错--Invalid bound statement
报错如下 org.apache.ibatis.binding.BindingException: Invalid bound statement (not found): com.lotus.mybatis.mapper.UserMapper.selectListat org.apache.ibatis.binding.MapperMethod$SqlCommand.<init>(MapperMethod.java:235)at com.baomidou.mybatisplus.cor…...
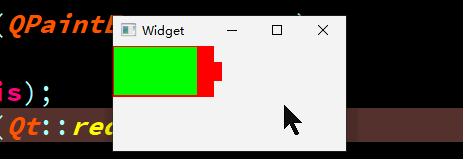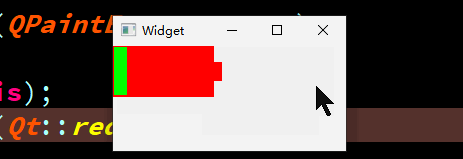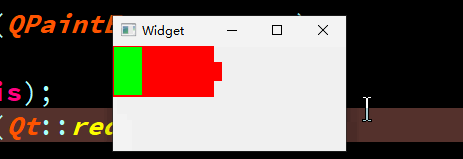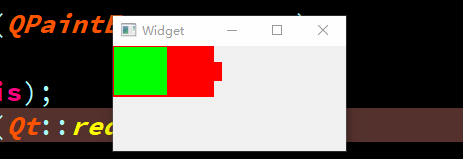
QT-QPainter实现一个动态充电的电池
1、效果 2、核心代码 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTimer>...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

【汇编逆向系列】六、函数调用包含多个参数之多个整型-参数压栈顺序,rcx,rdx,r8,r9寄存器
从本章节开始,进入到函数有多个参数的情况,前面几个章节中介绍了整型和浮点型使用了不同的寄存器在进行函数传参,ECX是整型的第一个参数的寄存器,那么多个参数的情况下函数如何传参,下面展开介绍参数为整型时候的几种情…...

