扩散模型详细推导过程——编码与解码
符号表
| 符号 | 含义 |
|---|---|
| x ( i ) = z 0 ( i ) \boldsymbol{x}^{(i)}=\boldsymbol{z}_0^{(i)} x(i)=z0(i) | 第 i i i个训练数据,其为长度为 d d d的向量 |
| z t ( i ) \boldsymbol{z}_t^{(i)} zt(i) | 第 i i i个训练数据在第 t t t时刻的加噪版本 |
| ϵ t ( i ) \boldsymbol{\epsilon}_t^{(i)} ϵt(i) | 第 i i i个训练数据在第 t t t时刻所添加的高斯噪声 |
| β t \beta_t βt | 噪声计划(noise schedule),范围为[0,1] |
| α t \alpha_t αt | α t = ∏ s = 1 t ( 1 − β s ) \alpha_t=\prod_{s=1}^t (1-\beta_s) αt=∏s=1t(1−βs) |
| N ( μ , σ 2 I ) N(\boldsymbol{\mu},\sigma^2\boldsymbol{I}) N(μ,σ2I) | 均值为 μ \boldsymbol{\mu} μ,标准差为 σ \sigma σ的高斯分布 |
| q ( ⋅ ) q\left(·\right) q(⋅) | 正向过程的转移核 |
| p ( ⋅ ) p(·) p(⋅) | 反向过程的转移核 |
| p ( ⋅ ∣ θ ) p\left(·|\theta\right) p(⋅∣θ) | 受参数 θ \theta θ影响,用于拟合反向过程的真实概率密度函数 |
| f t f_t ft | 反向过程中 t t t时刻对应的神经网络 |
| g t g_t gt | 反向过程中 t t t时刻对应的神经网络 |
| θ t \theta_t θt | 神经网络 f t f_t ft或 g t g_t gt的参数 |
| θ 1 : T \theta_{1:T} θ1:T | θ 1 , θ 2 , ⋯ , θ T \theta_1,\theta_2,\cdots,\theta_T θ1,θ2,⋯,θT |
| d z 1 : T d\boldsymbol{z}_{1:T} dz1:T | d z 1 d z 2 ⋯ d z T d\boldsymbol{z}_1d\boldsymbol{z}_2\cdots d\boldsymbol{z}_T dz1dz2⋯dzT |
| 注: | 如没有上标 ( i ) ^{(i)} (i),则表明在此语境下不特别指明对应某个样本 |
扩散模型的扩散过程(编码器)
扩散模型的编码器所做的工作如下:
设有原数据 x \boldsymbol{x} x,经过如下的逐步编码(添加噪声)过程可以得到一个符合标准高斯分布的噪声
z t = 1 − β t z t − 1 + β t ϵ t , t = 1 , 2 , ⋯ , T \begin{equation}\boldsymbol{z}_t=\sqrt{1-\beta_t}\boldsymbol{z}_{t-1}+\sqrt{\beta_t}\boldsymbol{\epsilon}_t, t=1,2,\cdots,T\end{equation} zt=1−βtzt−1+βtϵt,t=1,2,⋯,T
其中 z 0 = x \boldsymbol{z}_0=\boldsymbol{x} z0=x, ϵ 1 , ϵ 2 , ⋯ , ϵ t ∼ N ( 0 , I ) \boldsymbol{\epsilon}_1, \boldsymbol{\epsilon}_2,\cdots,\boldsymbol{\epsilon}_t\sim N(\boldsymbol{0}, \boldsymbol{I}) ϵ1,ϵ2,⋯,ϵt∼N(0,I), β 1 , β 2 , ⋯ , β t ∈ [ 0 , 1 ] \beta_1,\beta_2,\cdots,\beta_t\in [0,1] β1,β2,⋯,βt∈[0,1]为噪声计划(noise schedule),一般逐级递增。当 T → ∞ T\rightarrow \infty T→∞, z T \boldsymbol{z}_T zT将服从高斯分布,该推导在下面会涉及。
由于每一步的扩散结果 z t \boldsymbol{z}_t zt仅依赖于上一个扩散结果 z t − 1 \boldsymbol{z}_{t-1} zt−1,也即只要已知 z t − 1 \boldsymbol{z}_{t-1} zt−1(不需要再知道 z 1 , z 2 , ⋯ , z t − 2 \boldsymbol{z}_{1},\boldsymbol{z}_{2},\cdots,\boldsymbol{z}_{t-2} z1,z2,⋯,zt−2),再经过计算便可以得到 z t \boldsymbol{z}_{t} zt。该扩散特点符合马尔科夫链的性质,即每一时刻的状态仅依赖于上一时刻的状态,而与之前的状态无关。
现在用一个马尔科夫链表达该扩散过程。在 z t − 1 \boldsymbol{z}_{t-1} zt−1是已知的情况下, z t \boldsymbol{z}_t zt的均值
E [ z t ] = E [ 1 − β t z t − 1 ] + E [ β t ϵ t ] = 1 − β t z t − 1 + 0 = 1 − β t z t − 1 \begin{align}E[\boldsymbol{z}_t]&=E[\sqrt{1-\beta_t}\boldsymbol{z}_{t-1}]+E[\sqrt{\beta_t}\boldsymbol{\epsilon}_t]\\&=\sqrt{1-\beta_t}\boldsymbol{z}_{t-1}+\boldsymbol{0}\\&=\sqrt{1-\beta_t}\boldsymbol{z}_{t-1}\end{align} E[zt]=E[1−βtzt−1]+E[βtϵt]=1−βtzt−1+0=1−βtzt−1
z t \boldsymbol{z}_t zt的方差
C o v [ z t ] = C o v [ 1 − β t z t − 1 ] + C o v [ β t ϵ t ] = 0 + ( β t ) 2 I = β t I \begin{align}Cov[\boldsymbol{z}_t]&=Cov[\sqrt{1-\beta_t}\boldsymbol{z}_{t-1}]+Cov[\sqrt{\beta_t}\boldsymbol{\epsilon}_t]\\ &= \boldsymbol{0}+(\sqrt{\beta_t})^2\boldsymbol{I}\\ &= \beta_t\boldsymbol{I}\end{align} Cov[zt]=Cov[1−βtzt−1]+Cov[βtϵt]=0+(βt)2I=βtI
以上推导源自于:① z t − 1 \boldsymbol{z}_{t-1} zt−1是已知的,它不是分布,而是常量② ϵ t \boldsymbol{\epsilon}_t ϵt是标准的高斯分布③若 x ∼ N ( m x , Σ x ) \boldsymbol{x}\sim N(\boldsymbol{m}_{x},\boldsymbol{\Sigma}_{x}) x∼N(mx,Σx), y ∼ N ( m y , Σ y ) \boldsymbol{y}\sim N(\boldsymbol{m}_y,\boldsymbol{\Sigma}_y) y∼N(my,Σy),则 A x + B y + c ∼ N ( A m x + B m y + c , A Σ x A T + B Σ y B T ) \boldsymbol{Ax}+\boldsymbol{By}+\boldsymbol{c}\sim N(\boldsymbol{Am}_x+\boldsymbol{Bm}_y+\boldsymbol{c},\boldsymbol{A\Sigma_{x}A}^T+\boldsymbol{B\Sigma_{y}B}^T) Ax+By+c∼N(Amx+Bmy+c,AΣxAT+BΣyBT)
根据前面的分析,在已知 z t − 1 \boldsymbol{z}_{t-1} zt−1的情况下, z t \boldsymbol{z}_t zt的概率分布,即转移核的表达式如下:
q ( z t ∣ z t − 1 ) = N ( 1 − β t z t − 1 , β t I ) = 1 ( 2 π ) d 2 β t exp ( − ( z t − 1 − β t z t − 1 ) 2 2 β t ) \begin{equation}q(\boldsymbol{z}_t|\boldsymbol{z}_{t-1})=N(\sqrt{1-\beta_t}\boldsymbol{z}_{t-1},\beta_t\boldsymbol{I})=\frac{1}{(2\pi)^{\frac{d}{2}}\sqrt{\beta_t}}\exp{\left(-\frac{(\boldsymbol{z}_{t}-\sqrt{1-\beta_t}\boldsymbol{z}_{t-1})^2}{2\beta_t}\right)}\end{equation} q(zt∣zt−1)=N(1−βtzt−1,βtI)=(2π)2dβt1exp(−2βt(zt−1−βtzt−1)2)
该表达式使用了多元高斯分布的定义,即若随机变量 X = [ X 1 ⋯ X n ] T X=\begin{bmatrix}X_1\cdots X_n\end{bmatrix}^T X=[X1⋯Xn]T 服从均值为 μ ∈ R n \boldsymbol{\mu}\in\mathbb{R}^n μ∈Rn ,协方差为 Σ ∈ S + + n \boldsymbol{\Sigma}\in\mathbb{S}_{++}^n Σ∈S++n 的多元高斯分布,则其概率密度函数为:
1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) . \begin{aligned}\frac{1}{(2\pi)^{n/2}|\boldsymbol{\Sigma}|^{1/2}}\exp\left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right).\end{aligned} (2π)n/2∣Σ∣1/21exp(−21(x−μ)TΣ−1(x−μ)).
因此,在已知 x \boldsymbol{x} x的情况下,将通过 q ( z 1 ∣ x ) q(\boldsymbol{z}_1|\boldsymbol{x}) q(z1∣x)采样得到 z 1 \boldsymbol{z}_1 z1;则 z 1 \boldsymbol{z}_1 z1变为已知,再通过 q ( z 2 ∣ z 1 ) q(\boldsymbol{z}_2|\boldsymbol{z}_1) q(z2∣z1)采样得到 z 2 \boldsymbol{z}_2 z2,类似地递推,最后得到 x T \boldsymbol{x}_T xT。当 T T T非常大的时候,该过程十分耗时,但可以将 z t \boldsymbol{z}_t zt中的 z t − 1 \boldsymbol{z}_{t-1} zt−1逐层次替换为 x \boldsymbol{x} x的表达式,得到
z t = 1 − β t z t − 1 + β t ϵ t = 1 − β t ( 1 − β t − 1 z t − 2 + β t − 1 ϵ t − 1 ) + β t ϵ t = ( 1 − β t ) ( 1 − β t − 1 ) z t − 2 + 1 − β t − ( 1 − β t ) ( 1 − β t − 1 ) ϵ t − 1 + β t ϵ t \begin{aligned} \boldsymbol{z}_{t}& =\sqrt{1-\beta_t}\boldsymbol{z}_{t-1}+\sqrt{\beta_t}\boldsymbol{\epsilon}_{t} \\ &=\sqrt{1-\beta_t}\left(\sqrt{1-\beta_{t-1}}\boldsymbol{z}_{t-2}+\sqrt{\beta_{t-1}}\boldsymbol{\epsilon}_{t-1}\right)+\sqrt{\beta_t}\boldsymbol{\epsilon}_{t} \\ &=\sqrt{(1-\beta_t)(1-\beta_{t-1})}\boldsymbol{z}_{t-2}+\sqrt{1-\beta_t-(1-\beta_t)(1-\beta_{t-1})}\boldsymbol{\epsilon}_{t-1}+\sqrt{\beta_t}\boldsymbol{\epsilon}_{t} \end{aligned} zt=1−βtzt−1+βtϵt=1−βt(1−βt−1zt−2+βt−1ϵt−1)+βtϵt=(1−βt)(1−βt−1)zt−2+1−βt−(1−βt)(1−βt−1)ϵt−1+βtϵt
再根据高斯分布的混合公式,将 ϵ t − 1 \boldsymbol{\epsilon_{t-1}} ϵt−1和 ϵ t \boldsymbol{\epsilon}_{t} ϵt的项混合为 ϵ \boldsymbol{\epsilon} ϵ的分布,得到
z t = ( 1 − β t ) ( 1 − β t − 1 ) z t − 2 + ( 1 − β t ) − ( 1 − β t ) ( 1 − β t − 1 ) 2 + β t 2 ϵ = ( 1 − β t ) ( 1 − β t − 1 ) z t − 2 + 1 − β t − ( 1 − β t ) ( 1 − β t − 1 ) + β t ϵ = ( 1 − β t ) ( 1 − β t − 1 ) z t − 2 + 1 − ( 1 − β t ) ( 1 − β t − 1 ) ϵ = … = ∏ i = 1 t ( 1 − β i ) x + 1 − ∏ i = 1 t ( 1 − β i ) ϵ = α t x + 1 − α t ϵ , t = 1 , 2 , ⋯ , T \begin{align*} \boldsymbol{z}_{t}&=\sqrt{(1-\beta_t)(1-\beta_{t-1})}\boldsymbol{z}_{t-2}+\sqrt{\sqrt{(1-\beta_t)-(1-\beta_t)(1-\beta_{t-1})}^2+\sqrt{\beta_t}^2}\boldsymbol{\epsilon} \\ &=\sqrt{(1-\beta_t)(1-\beta_{t-1})}\boldsymbol{z}_{t-2}+\sqrt{1-\beta_t-(1-\beta_t)(1-\beta_{t-1})+\beta_t}\boldsymbol{\epsilon} \\ &=\sqrt{(1-\beta_t)(1-\beta_{t-1})}\boldsymbol{z}_{t-2}+\sqrt{1-(1-\beta_t)(1-\beta_{t-1})}\boldsymbol{\epsilon} \\ &=\ldots \\ &=\sqrt{\prod_{i=1}^t(1-\beta_i)}\boldsymbol{x}+\sqrt{1-\prod_{i=1}^t(1-\beta_i)}\boldsymbol{\epsilon} \\ &=\sqrt{\alpha_t}\boldsymbol{x}+\sqrt{1-\alpha_t}\boldsymbol{\epsilon},t=1,2,\cdots,T \end{align*} zt=(1−βt)(1−βt−1)zt−2+(1−βt)−(1−βt)(1−βt−1)2+βt2ϵ=(1−βt)(1−βt−1)zt−2+1−βt−(1−βt)(1−βt−1)+βtϵ=(1−βt)(1−βt−1)zt−2+1−(1−βt)(1−βt−1)ϵ=…=i=1∏t(1−βi)x+1−i=1∏t(1−βi)ϵ=αtx+1−αtϵ,t=1,2,⋯,T
为了区分不同时刻所对应的噪声,对 ϵ \boldsymbol{\epsilon} ϵ添加下标 t t t,可得
z t = α t x + 1 − α t ϵ t , t = 1 , 2 , ⋯ , T \begin{equation}\boldsymbol{z}_t=\sqrt{\alpha_t}\boldsymbol{x}+\sqrt{1-\alpha_t}\boldsymbol{\epsilon}_t, t=1,2,\cdots,T\end{equation} zt=αtx+1−αtϵt,t=1,2,⋯,T
其中, α t = ∏ s = 1 t ( 1 − β s ) \alpha_t=\prod_{s=1}^t (1-\beta_s) αt=∏s=1t(1−βs), ϵ ∼ N ( 0 , I ) \boldsymbol{\epsilon}\sim N(\boldsymbol{0}, \boldsymbol{I}) ϵ∼N(0,I)。
所以,一旦已知 x \boldsymbol{x} x,便可以得到 z t \boldsymbol{z}_t zt的分布,故:
q ( z t ∣ x ) = N ( α t x , ( 1 − α t ) I ) = 1 ( 2 π ) d 2 ( 1 − α t ) exp ( − ( z t − α t x ) 2 1 − α t ) \begin{equation}q(\boldsymbol{z}_t|\boldsymbol{x})=N(\sqrt{\alpha_t}\boldsymbol{\boldsymbol{x}},(1-\alpha_t)\boldsymbol{I})=\frac{1}{(2\pi)^{\frac{d}{2}}\sqrt{(1-\alpha_t)}}\exp{\left(-\frac{(\boldsymbol{z}_{t}-\sqrt{\alpha_t}\boldsymbol{x})^2}{1-\alpha_t}\right)}\end{equation} q(zt∣x)=N(αtx,(1−αt)I)=(2π)2d(1−αt)1exp(−1−αt(zt−αtx)2)
因此, z t \boldsymbol{z}_t zt可以通过先从标准的高斯分布中采样 ϵ \boldsymbol{\epsilon} ϵ,然后和 z 0 \boldsymbol{z}_0 z0进行混合得到。另外可以观察到,因为 β t \beta_t βt在 t t t很大的时候近似为 1 1 1,那么 α t \alpha_t αt在 t t t很大的时候近似等于0,此时 q ( z t ∣ x ) q(\boldsymbol{z}_t|\boldsymbol{x}) q(zt∣x)近似为一个标准的高斯分布。
扩散模型的去噪过程(解码器)
扩散模型的解码器是为了反转编码过程。如果知道逆向转移核 p ( z t − 1 ∣ z t ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t}) p(zt−1∣zt),那么就可以先从 p ( z T ) = N ( 0 , I ) p(\boldsymbol{z}_T)=N(\boldsymbol{0},\boldsymbol{I}) p(zT)=N(0,I)采样出 z T \boldsymbol{z}_T zT,再通过 p ( z T − 1 ∣ z T ) p(\boldsymbol{z}_{T-1}|\boldsymbol{z}_{T}) p(zT−1∣zT)采样出 z T − 1 \boldsymbol{z}_{T-1} zT−1,依次类推,直到采样出 z 0 \boldsymbol{z}_{0} z0,即 x \boldsymbol{x} x。
贝叶斯公式给出了根据 q ( z t ∣ z t − 1 ) q(\boldsymbol{z}_{t}|\boldsymbol{z}_{t-1}) q(zt∣zt−1)求出 p ( z t − 1 ∣ z t ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t}) p(zt−1∣zt)的方法,即
p ( z t − 1 ∣ z t ) = q ( z t ∣ z t − 1 ) q ( z t − 1 ) q ( z t ) \begin{equation}p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t})=\frac{q(\boldsymbol{z}_{t}|\boldsymbol{z}_{t-1})q(\boldsymbol{z}_{t-1})}{q(\boldsymbol{z}_t)}\end{equation} p(zt−1∣zt)=q(zt)q(zt∣zt−1)q(zt−1)
观察该式可知,由于 q ( z t − 1 ) / q ( z t ) q(\boldsymbol{z}_{t-1})/q(\boldsymbol{z}_{t}) q(zt−1)/q(zt)是未知的,所以求不出任何结果,而且实际上该逆向转移核不一定是高斯分布。
但是,如果给定额外条件 x \boldsymbol{x} x,由(15),可以得到
p ( z t − 1 ∣ z t , x ) = q ( z t ∣ z t − 1 , x ) q ( z t − 1 ∣ x ) q ( z t ∣ x ) \begin{equation}p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\boldsymbol{x})=\frac{q(\boldsymbol{z}_{t}|\boldsymbol{z}_{t-1},\boldsymbol{x})q(\boldsymbol{z}_{t-1}|\boldsymbol{x})}{q(\boldsymbol{z}_t|\boldsymbol{x})}\end{equation} p(zt−1∣zt,x)=q(zt∣x)q(zt∣zt−1,x)q(zt−1∣x)
根据马尔科夫链的性质 q ( z t ∣ z t − 1 , x ) = q ( z t ∣ z t − 1 ) q(\boldsymbol{z}_{t}|\boldsymbol{z}_{t-1},\boldsymbol{x})=q(\boldsymbol{z}_{t}|\boldsymbol{z}_{t-1}) q(zt∣zt−1,x)=q(zt∣zt−1),结合公式(8)和(10),经过很复杂的一段化简(省略过程)得到:
p ( z t − 1 ∣ z t , x ) = q ( z t ∣ z t − 1 ) q ( z t − 1 ∣ x ) q ( z t ∣ x ) ∝ q ( z t ∣ z t − 1 ) q ( z t − 1 ∣ x ) = N z t ( 1 − β t ⋅ z t − 1 , β t I ) N z t − 1 ( α t − 1 ⋅ x , ( 1 − α t − 1 ) I ) \begin{aligned} p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\boldsymbol{x})& =\quad\frac{q(\boldsymbol{z}_t|\boldsymbol{z}_{t-1})q(\boldsymbol{z}_{t-1}|\boldsymbol{x})}{q(\boldsymbol{z}_t|\boldsymbol{x})} \\ &\propto\quad q(\boldsymbol{z}_t|\boldsymbol{z}_{t-1})q(\boldsymbol{z}_{t-1}|\boldsymbol{x}) \\ &=\quad N_{\boldsymbol{z}_t}\left(\sqrt{1-\beta_t}\cdot\boldsymbol{z}_{t-1},\beta_t\boldsymbol{I}\right)N_{\boldsymbol{z}_{t-1}}\left(\sqrt{\alpha_{t-1}}\cdot\boldsymbol{x},(1-\alpha_{t-1})\boldsymbol{I}\right) \\\end{aligned} p(zt−1∣zt,x)=q(zt∣x)q(zt∣zt−1)q(zt−1∣x)∝q(zt∣zt−1)q(zt−1∣x)=Nzt(1−βt⋅zt−1,βtI)Nzt−1(αt−1⋅x,(1−αt−1)I)
根据高斯随机变量的变量替换定理,即
N v [ A w , B ] ∝ N w [ ( A T B − 1 A ) − 1 A T B − 1 v , ( A T B − 1 A ) − 1 ] N_{\boldsymbol{v}}\left[\boldsymbol{A}\boldsymbol{w},\boldsymbol{B}\right]\propto N_{\boldsymbol{w}}\left[\left(\boldsymbol{A}^T\boldsymbol{B}^{-1}\boldsymbol{A}\right)^{-1}\boldsymbol{A}^T\boldsymbol{B}^{-1}\boldsymbol{v},\left(\boldsymbol{A}^T\boldsymbol{B}^{-1}\boldsymbol{A}\right)^{-1}\right] Nv[Aw,B]∝Nw[(ATB−1A)−1ATB−1v,(ATB−1A)−1]
可得,
N z t ( 1 − β t ⋅ z t − 1 , β t I ) N z t − 1 ( α t − 1 ⋅ x , ( 1 − α t − 1 ) I ) ∝ N z t − 1 ( 1 1 − β t z t , β t 1 − β t I ) N z t − 1 ( α t − 1 ⋅ x , ( 1 − α t − 1 ) I ) \quad N_{\boldsymbol{z}_t}\left(\sqrt{1-\beta_t}\cdot\boldsymbol{z}_{t-1},\beta_t\boldsymbol{I}\right)N_{\boldsymbol{z}_{t-1}}\left(\sqrt{\alpha_{t-1}}\cdot\boldsymbol{x},(1-\alpha_{t-1})\boldsymbol{I}\right)\propto N_{\boldsymbol{z}_{t-1}}\left(\frac{1}{\sqrt{1-\beta_t}}\boldsymbol{z}_t,\frac{\beta_t}{1-\beta_t}\boldsymbol{I}\right)N_{\boldsymbol{z}_{t-1}}\left(\sqrt{\alpha_{t-1}}\cdot\boldsymbol{x},(1-\alpha_{t-1})\boldsymbol{I}\right) Nzt(1−βt⋅zt−1,βtI)Nzt−1(αt−1⋅x,(1−αt−1)I)∝Nzt−1(1−βt1zt,1−βtβtI)Nzt−1(αt−1⋅x,(1−αt−1)I)
再根据
N w [ a , A ] ⋅ N w [ b , B ] ∝ N w [ ( A − 1 + B − 1 ) − 1 ( A − 1 a + B − 1 b ) , ( A − 1 + B − 1 ) − 1 ] \begin{aligned}N_{\boldsymbol{w}}[\boldsymbol{a},\boldsymbol{A}]\cdot N_{\boldsymbol{w}}[\boldsymbol{b},\boldsymbol{B}]\propto N_{\boldsymbol{w}}&\left[\left(\boldsymbol{A}^{-1}+\boldsymbol{B}^{-1}\right)^{-1}(\boldsymbol{A}^{-1}\boldsymbol{a}+\boldsymbol{B}^{-1}\boldsymbol{b}),\left(\boldsymbol{A}^{-1}+\boldsymbol{B}^{-1}\right)^{-1}\right]\end{aligned} Nw[a,A]⋅Nw[b,B]∝Nw[(A−1+B−1)−1(A−1a+B−1b),(A−1+B−1)−1]
最终得到
p ( z t − 1 ∣ z t , x ) = N z t − 1 [ ( 1 − α t − 1 ) 1 − α t 1 − β t z t + α t − 1 β t 1 − α t x , β t ( 1 − α t − 1 ) 1 − α t I ] p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_t,\boldsymbol{x})=N_{\boldsymbol{z}_{t-1}}\left[\frac{(1-\alpha_{t-1})}{1-\alpha_t}\sqrt{1-\beta_t}\boldsymbol{z}_t+\frac{\sqrt{\alpha_{t-1}}\beta_t}{1-\alpha_t}\boldsymbol{x},\frac{\beta_t(1-\alpha_{t-1})}{1-\alpha_t}\boldsymbol{I}\right] p(zt−1∣zt,x)=Nzt−1[1−αt(1−αt−1)1−βtzt+1−αtαt−1βtx,1−αtβt(1−αt−1)I]
由此可知 p ( z t − 1 ∣ z t , x ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\boldsymbol{x}) p(zt−1∣zt,x)是一个高斯分布。
因此,尽管 p ( z t − 1 ∣ z t ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t}) p(zt−1∣zt)不是高斯分布,但给定条件 x \boldsymbol{x} x后得到的 p ( z t − 1 ∣ z t , x ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\boldsymbol{x}) p(zt−1∣zt,x)是高斯分布。另外,如果 p ( z t − 1 ∣ z t , x ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\boldsymbol{x}) p(zt−1∣zt,x)的均值和方差被确定,那么进一步可以写出从中采样的公式,得到 z t − 1 \boldsymbol{z}_{t-1} zt−1。因此,可以考虑用神经网络来近似 p ( z t − 1 ∣ z t , x ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\boldsymbol{x}) p(zt−1∣zt,x)(在后续训练目标的推导中可以看出网络的目标实际上是近似 p ( z t − 1 ∣ z t , x ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\boldsymbol{x}) p(zt−1∣zt,x)),记作 p ( z t − 1 ∣ z t , θ t ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\theta_t) p(zt−1∣zt,θt)。为了简化该分布,将其方差设为固定值,神经网络仅仅估计其均值。
p ( z t − 1 ∣ z t , θ t ) = N ( f t ( z t , θ t ) , σ t 2 I ) \begin{equation}p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\theta_t)=N(f_t(\boldsymbol{z}_t,\theta_t),\sigma_t^2\boldsymbol{I})\end{equation} p(zt−1∣zt,θt)=N(ft(zt,θt),σt2I)
其中 f t f_t ft为神经网络,其接受输入 z t \boldsymbol{z}_t zt并输出一个估计的均值, θ t \theta_t θt为该网络的参数, σ t \sigma_t σt为人为设定的标准差。
如果能训练出使得原数据 z 0 \boldsymbol{z}_0 z0总体出现概率最大的神经网络 f t ( z t , θ t ) f_t(\boldsymbol{z}_t,\theta_t) ft(zt,θt),进而得到 p ( z t − 1 ∣ z t , θ t ) p(\boldsymbol{z}_{t-1}|\boldsymbol{z}_{t},\theta_t) p(zt−1∣zt,θt),那么就可以先从 N ( 0 , I ) N(\boldsymbol{0},\boldsymbol{I}) N(0,I)采样出 z T \boldsymbol{z}_T zT,再通过 p ( z T − 1 ∣ z T , θ t ) p(\boldsymbol{z}_{T-1}|\boldsymbol{z}_{T},\theta_t) p(zT−1∣zT,θt)采样出 z T − 1 \boldsymbol{z}_{T-1} zT−1,依次类推,直到采样出 x \boldsymbol{x} x,即 z 0 \boldsymbol{z}_{0} z0。
相关文章:

扩散模型详细推导过程——编码与解码
符号表 符号含义 x ( i ) z 0 ( i ) \boldsymbol{x}^{(i)}\boldsymbol{z}_0^{(i)} x(i)z0(i)第 i i i个训练数据,其为长度为 d d d的向量 z t ( i ) \boldsymbol{z}_t^{(i)} zt(i)第 i i i个训练数据在第 t t t时刻的加噪版本 ϵ t ( i ) \boldsymbol{\epsilo…...

js如何实现开屏弹窗
开屏弹窗是什么,其实就是第一次登录后进入页面给你的一种公告提示,此后再回到当前这个页面时弹窗是不会再出现的。也就是说这个弹窗只会出现一次。 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>…...

C#——文件读取Directory类详情
文件读取Directory类 Durectory提供了目录以及子目录进行创建移动和列举操作方法 Directory和Directorylnfo类(主要操作文件目录属性列如文件是否隐藏的 或者只读等这些属性) Directory对目录进行复制、移动、重命名、创建和删除等操作DirectoryInfo用于对目录属性执行操作 …...

Ruby on Rails Post项目设置网站初始界面
在构建了Ruby的Web服务器后,第三步就可以去掉框架的官方页面,设置自己的网页初始页了。 Linux系统安装Ruby语言-CSDN博客 、在Ubuntu中创建Ruby on Rails项目并搭建数据库-CSDN博客、 Ruby语言建立Web服务器-CSDN博客 了解Ruby onRails项目中的主要文件…...

03-QTWebEngine中使用qtvirtualkeyboard
qt提供了 virtualKeyboard 虚拟键盘模块,只需要在在main函数中最开始加入这样一句就可以了 qputenv("QT_IM_MODULE", QByteArray("qtvirtualkeyboard")); 但是在使用的时候遇到了一些问题: 1、中文输入的时候没有输入提示 Qvirt…...
)
leetcode3无重复字符的最长字串(重点讲滑动窗口)
本文主要讲解无重复字符的最长字串的要点与细节,根据步骤一步步走更方便理解 c与java代码如下,末尾 具体要点: 1. 区分一下子串和子序列 子串:要求元素在母串中是连续地出现 子序列:不要求连续 2. 题目中有两个核心…...
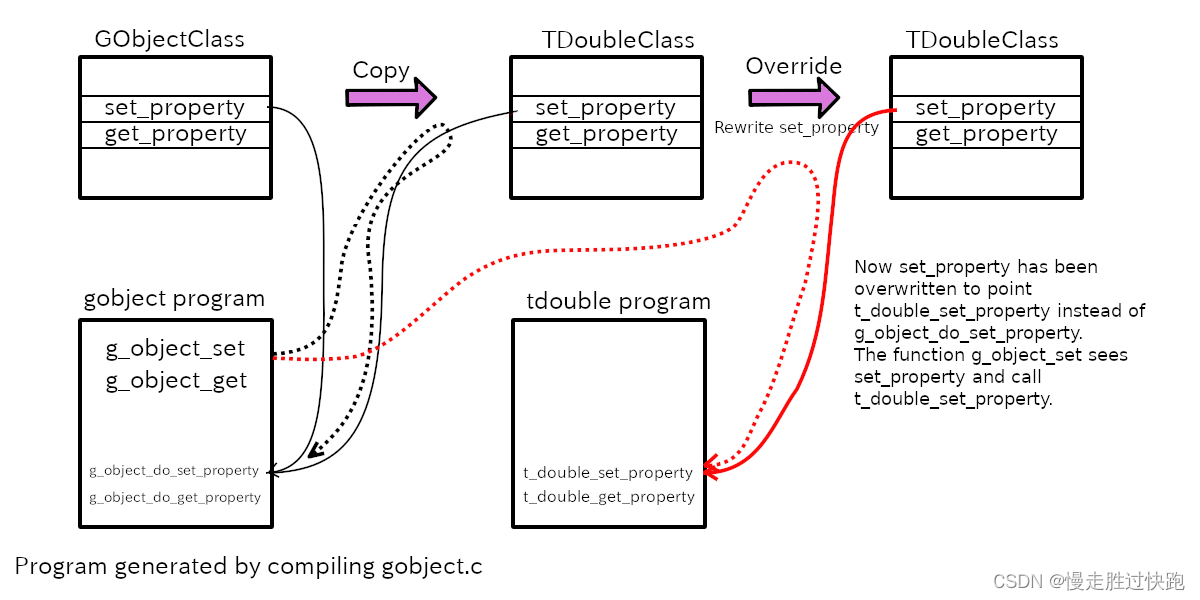
Gobject tutorial 八
The GObject base class Object memory management Gobject的内存管理相关的API很复杂,但其目标是提供一个基于引用计数的灵活的内存管理模式。 下面我们来介绍一下,与管理引用计数相关的函数。 Reference Count 函数g_object_ref和g_object_unref的…...

DDMA信号处理以及数据处理的流程---cfar检测
Hello,大家好,我是Xiaojie,好久不见,欢迎大家能够和Xiaojie一起学习毫米波雷达知识,Xiaojie准备连载一个系列的文章—DDMA信号处理以及数据处理的流程,本系列文章将从目标生成、信号仿真、测距、测速、cfar检测、测角、目标聚类、目标跟踪这几个模块逐步介绍,这个系列的…...
【机器学习】从理论到实践:决策树算法在机器学习中的应用与实现
📝个人主页:哈__ 期待您的关注 目录 📕引言 ⛓决策树的基本原理 1. 决策树的结构 2. 信息增益 熵的计算公式 信息增益的计算公式 3. 基尼指数 4. 决策树的构建 🤖决策树的代码实现 1. 数据准备 2. 决策树模型训练 3.…...

Zookeeper 集群节点故障剔除、切换、恢复原理
Zookeeper 集群节点故障剔除、切换、恢复原理 zookeeper 集群节点故障时,如何剔除节点,如果为领导节点如何处理,如何进行故障恢 复的,实现原理? 在 Zookeeper 集群中,当节点故障时,集群需要自动剔除故障节点并进行故障恢复,确保集群的高 可用性和一致性。具体来说,…...

解决帝国cms栏目管理拼音乱码的问题
帝国CMS7.5版本utf-8版网站后台增加栏目生成乱码的问题怎么解决 1、需要改一个函数,并且增加一个处理文件,方法如下: 修改e/class/connect.php文件,找到ReturnPinyinFun函数,如未修改文件在4533-4547行,将…...

Git快速入门
一 快速使用 1.1 初始化 什么是版本库呢?版本库又名仓库,可以简单理解成一个目录,这个目录里面的所有文件都可以被Git管理起来,每个文件的修改、删除,Git都能跟踪,以便任何时刻都可以追踪历史࿰…...

【18.0】JavaScript---事件案例
【18.0】JavaScript—事件案例 【一】开关灯事件 【介绍】设置一个按钮,按下按钮触发事件,来回切换圆形图片的颜色 【分析】 图片设置:设置成圆形的图片背景颜色:设置红绿两个颜色,来回切换按钮设置:点击…...
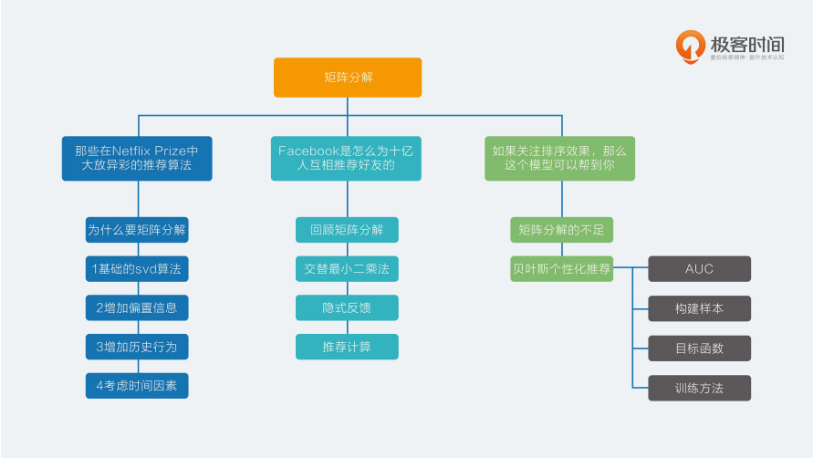
推荐系统三十六式学习笔记:原理篇.矩阵分解12|如果关注排序效果,那么这个模型可以帮到你
目录 矩阵分解的不足贝叶斯个性化排序AUC构造样本目标函数训练方法 总结 矩阵分解在推荐系统中的地位非常崇高。它既有协同过滤的血统,又有机器学习的基因,可以说是非常优秀了;但即便如此,传统的矩阵分解无论是在处理显式反馈&…...

Kafka之ISR机制的理解
文章目录 Kafka的基本概念什么是ISRISR的维护机制ISR的作用ISR相关配置参数同步过程示例代码总结 Kafka中的ISR(In-Sync Replicas同步副本)机制是确保数据高可用性和一致性的核心组件。 Kafka的基本概念 在Kafka中,数据被组织成主题…...
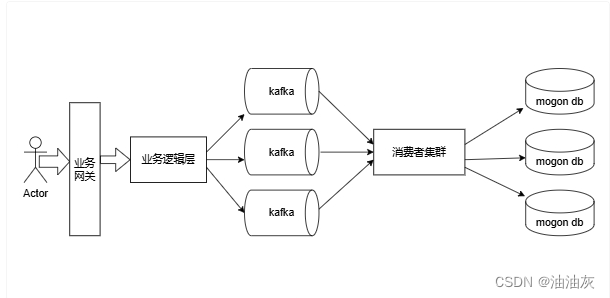
如何设计一个点赞系统
首先我们定义出一个点赞系统需要对外提供哪些接口: 1.用户对特定的消息进行点赞; 2.用户查看自己发布的某条消息点赞数量以及被哪些人赞过; 3.用户查看自己给哪些消息点赞过; 这里假设每条消息都有一个message_id, 每一个用户都…...

对象存储测试工具-s3cmd
一、环境安装 官网:https://s3tools.org/s3cmd 下载安装包:https://s3tools.org/download GitHub:https://github.com/s3tools/s3cmd/releases 本文安装包:https://github.com/s3tools/s3cmd/releases/download/v2.0.2/s3cmd-2.0…...

OpenCV--图像色彩空间及转换
图像色彩空间及转换 python代码和笔记 python代码和笔记 import cv2 色彩空间,基础:RGB或BGR OpenCV中: 一、HSV(HSB):用的最多, Hue:色相-色彩(0-360),红色:0,绿色&…...

RIP解决不连续子网问题
#交换设备 RIP解决不连续子网问题 一、不连续子网的概念 相同主网下的子网,被另一个主网分割,例如下面实验拓扑在某公司的网络整改项目中,原先R1 和RS 属于同一主网络 10.0.0.0/8,现被 R2、R3、R4 分离,整网采用了 …...

动态轮换代理IP是什么?有什么用?
如果您要处理多个在线帐户,选择正确的代理类型对于实现流畅的性能至关重要。但最适合这项工作的代理类型是什么? 为了更好地管理不同平台上的多个账户并优化成本,动态住宅代理IP通常作用在此。 一、什么是轮换代理? 轮换代理充当…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...
