C++进阶之AVL树
个人主页:点我进入主页
专栏分类:C语言初阶 C语言进阶 数据结构初阶 Linux C++初阶 C++进阶 算法
欢迎大家点赞,评论,收藏。
一起努力,一起奔赴大厂
目录
一.前言
二.插入
三.旋转
3.1右旋
3.2左旋
3.3左右双旋
3.4右左双旋
四.测试
一.前言
在看这篇博客之前需要了解二叉搜索树的相关内容,可以看这篇博客二叉搜索树,AVL树可以看成为了解决二叉搜索树的问题,它保证了左右子树高度差不超过1。本次的内容的重点就是对AVL树的旋转。
二.插入
AVL树的插入规则和二叉搜索树的插入规则类似,左子树都小于父节点,右子树都大于父节点,在这里我们引入了一个平衡因子,我们先插入后然后进行调节平衡因子,平衡因子的计算=右子树的高度-左子树的高度,插入的新节点的平衡因子为0,当插入的节点在父节点的右边,父节点的平衡因子+1,当插入的节点在父节点的左边,父节点的平衡因子-1,当整后父节点的平衡因子为0时直接结束,不需要继续调整,当调整后父节点的平衡因子为+1或者-1时需要继续向上进行调整,当调整后父节点的平衡因子为+2或-2时需要进行旋转。我们看下面的代码实现:
bool insert(const pair<K, V>& kv)
{Node* newnode = new Node(kv);if (_root == nullptr) _root = newnode;else{Node* cur = _root, * parent = nullptr;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first) {parent = cur;cur = cur->_right;}else return false;}if (kv.first < parent->_kv.first) parent->_left = newnode;else parent->_right = newnode;newnode->_parent = parent;//调整平衡因子while (parent){if (newnode == parent->_left) parent->_bf--;else parent->_bf++;if (parent->_bf == 0) break;else if (parent->_bf == 1 || parent->_bf == -1){newnode = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && newnode->_bf == 1){RatoteL(parent);}else if (parent->_bf == -2 && newnode->_bf == -1){RatoteR(parent);}else if (parent->_bf == 2 && newnode->_bf == -1){RatoteRL(parent);}else if (parent->_bf == -2 && newnode->_bf == 1){RatoteLR(parent);}else{assert(false);}break;}else{assert(false);}}}return true;
}三.旋转
旋转有4种方式:向右旋转,向左旋转,左右双旋,右左双旋这四种
3.1右旋
看下面的抽象图

当n=0时全图为
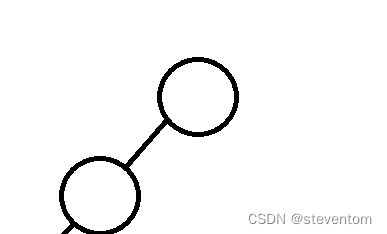
当n=1时全图为

当n=2时我们有3种,但是在a的位置能放第3种,因为别的会自动进行旋转,b和c这三种都可以
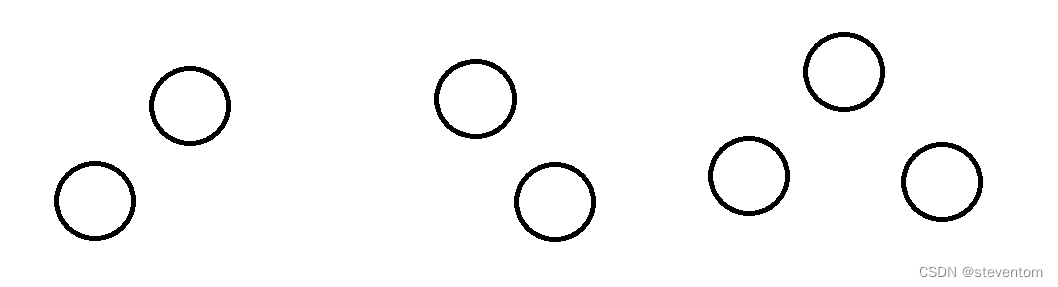
当n=3时就会更多,所以这是列举不完的,针对右旋我们以下面这张图为例:

我们经过右旋后转化成下面的样子,针对的主要就是这几个节点
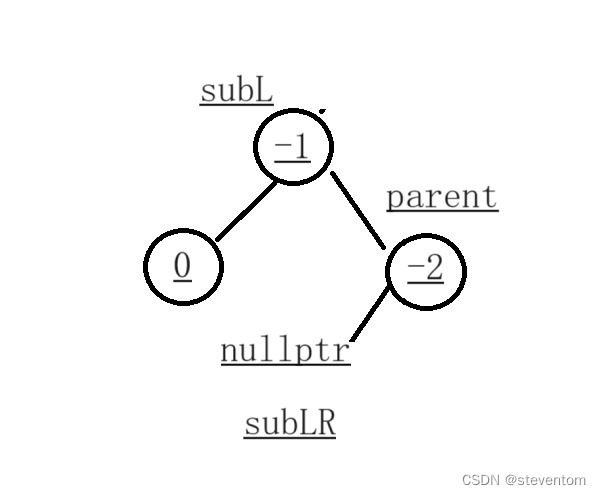
在旋转的过程中需要注意的是,parent节点是不是根节点,注意调整后subL节点的的父节点的调整,还有一点就是subLR是否为空节点,调整后需要将subL节点和parent节点的bf值改为0,我们看下面的代码:
void RatoteR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;Node* ppNode = parent->_parent;subL->_parent = parent->_parent;parent->_parent = subL;if (subLR)subLR->_parent = parent;if (parent == _root){_root = subL;}else{if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;}subL->_bf = parent->_bf = 0;}3.2左旋
左旋的代码和右旋的类似,不过需要调节的平衡因子为2和1,我们看下面的图片
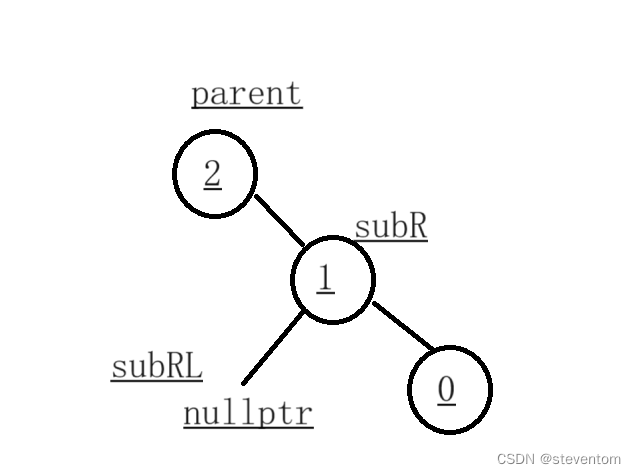
我们直接上代码:
void RatoteL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subR;subR->_left = parent;subR->_parent = ppNode;if (parent == _root){_root = subR;}else{if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;}subR->_bf = parent->_bf = 0;
}
void RatoteRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RatoteR(subR);RatoteL(parent);if (bf == 1){parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;}}3.3左右双旋
左右双旋的图片可以看为下面的抽象图:

当我们在b位置插入后再旋转,可以得到:

当我们插入到c位置后再经过旋转,可以得到:
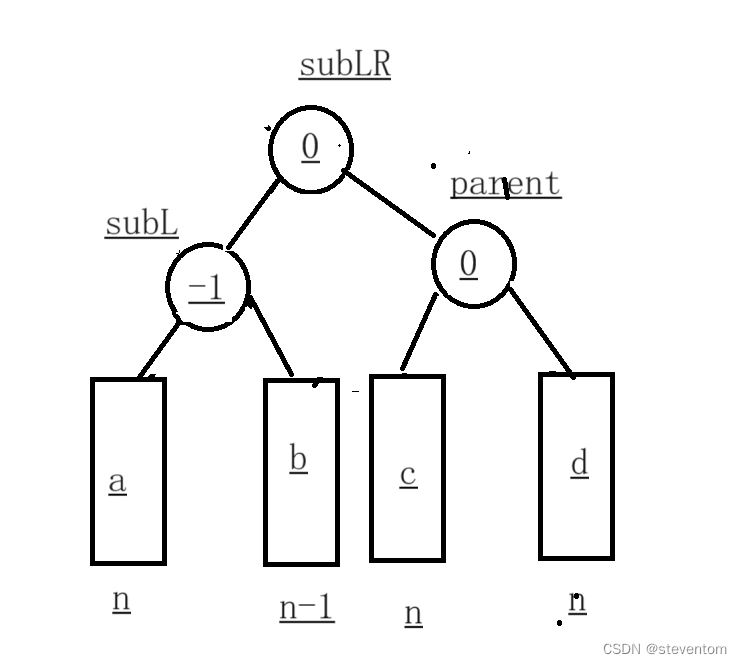
当只旋转一次就会做一次镜像旋转,我们先让subL节点左旋,然后让parent右旋,然后进行调节平衡因子,我们看代码:
void RatoteLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RatoteL(subL);RatoteR(parent);if (bf == 1){subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;}
}3.4右左双旋
这个和左右双旋类似,我们直接看代码:
void RatoteRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RatoteR(subR);RatoteL(parent);if (bf == 1){parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;}}四.测试
我们直接上代码:
public: void InOrder(){_InOrder(_root);}bool IsBalance(){return _IsBalance(_root);}
private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << "->" << root->_kv.second << endl;int left = _height(root->_left);int right = _height(root->_right);int sub = abs(left - right);cout << "bf-> " << sub<<endl;if (sub >= 2) cout<<"key-> "<< root->_kv.first << endl;_InOrder(root->_right);}int _height(Node* root){if (root == nullptr)return 0;int x = 1 + _height(root->_left);int y = 1 + _height(root->_right);return max(x , y);}bool _IsBalance(Node* root){ if (root == nullptr) return true;int left = _height(root->_left);int right = _height(root->_right);if (abs(right - left) >= 2){return false;}return _IsBalance(root->_left) && _IsBalance(root->_right);}测试代码:
int main()
{srand(0);AVLTree<int, int> a;vector<int> v;for (int i = 0; i < 1000000; i++){int num = rand() + i;v.push_back(num);}cout << a.IsBalance() << endl;return 0;
}运行可以看到:

相关文章:

C++进阶之AVL树
个人主页:点我进入主页 专栏分类:C语言初阶 C语言进阶 数据结构初阶 Linux C初阶 C进阶 算法 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂 目录 一.前言 二.插入 三.旋转 3.1右旋 …...

sizeof 和 strlen 比较
sizeof 和 strlen 在 C 语言中都是用于获取某种“大小”的,但它们之间有着显著的区别。 sizeof sizeof 是一个运算符,用于计算数据类型或对象在内存中的大小(以字节为单位)。它可以在编译时确定结果,因为它计算的是类…...

音视频开发—FFmpeg 打开摄像头进行RTMP推流
实验平台:Ubuntu20.04 摄像头:普通USB摄像头,输出格式为YUV422 1.配置RTMP服务器推流平台 使用Nginx 配置1935端口即可,贴上教程地址 ubuntu20.04搭建Nginxrtmp服务器) 2.配置FFmpeg开发环境 过程较为简单,这里不…...
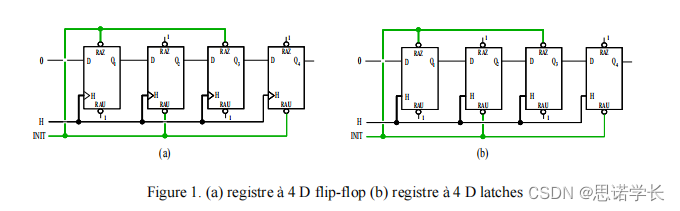
D触发器(D Flip-Flop)与D锁存器(D Latch)
1 基础概念 我们先来简单回顾一下D触发器(D flip-flop)和D锁存器(D latch)的概念,以及它们在数字电路中的作用。 1.1 D触发器(D Flip-Flop) D触发器是一种数字存储器件,它在时钟信号…...
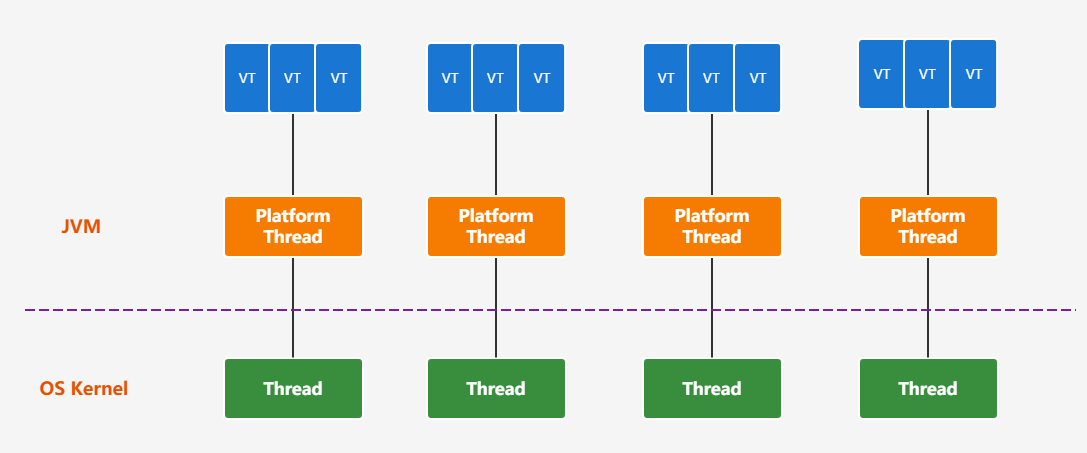
JDK19特性
JDK19特性 一、JAVA19概述 JDK 19 2022 年 9 月 20 日正式发布以供生产使用,非长期支持版本。不过,JDK 19 中有一些比较重要的新特性值得关注。 JDK 19 只有 7 个新特性: JEP 405: Record Patterns(记录模式)[1] (预览)JEP 422: Linux/RISC-V Port[2]JEP 424: Foreign …...

sql语句中常用的函数有那些
1、字符串函数 CONCAT(string1, string2, ...): 连接两个或多个字符串。 UPPER(string): 将字符串转换为大写。 LOWER(string): 将字符串转换为小写。 TRIM(string): 去除字符串两端的空格。 LENGTH(string): 返回字符串的长度。 SUBSTRING(string, start, length): 从字符串中…...

odoo17 小变更3 Warning、 “attrs “和 “states “不再用
odoo17 小变更 1、Warning from odoo.exceptions import ValidationError,Warning ImportError: cannot import name Warning from odoo.exceptions (D:\od172406\odoo\exceptions.py) 2、自 17.0 版起,不再使用 "attrs "和 "states "属性。 …...

Unity3d 游戏暂停(timeScale=0)引起的deltaTime关联的系列问题解决
问题描述 游戏暂停的功能是通过设置timeScale0实现的,不过在暂停游戏的时候,需要对角色进行预览和设置,为了实现这个功能,是通过鼠标控制相机的操作,为了使相机的操作丝滑,获取鼠标操作系数乘以Time.delta…...

服务端代码编写中MySql大小写在Java中报错问题解决
报错信息: 原因:MySql和Java变量大小写产生的冲突。 经过查阅各个博客等,得出浅显结论(不一定对):MySql大小写不敏感,Java大小写敏感,当Javabean转为MySql数据库表时,Ja…...
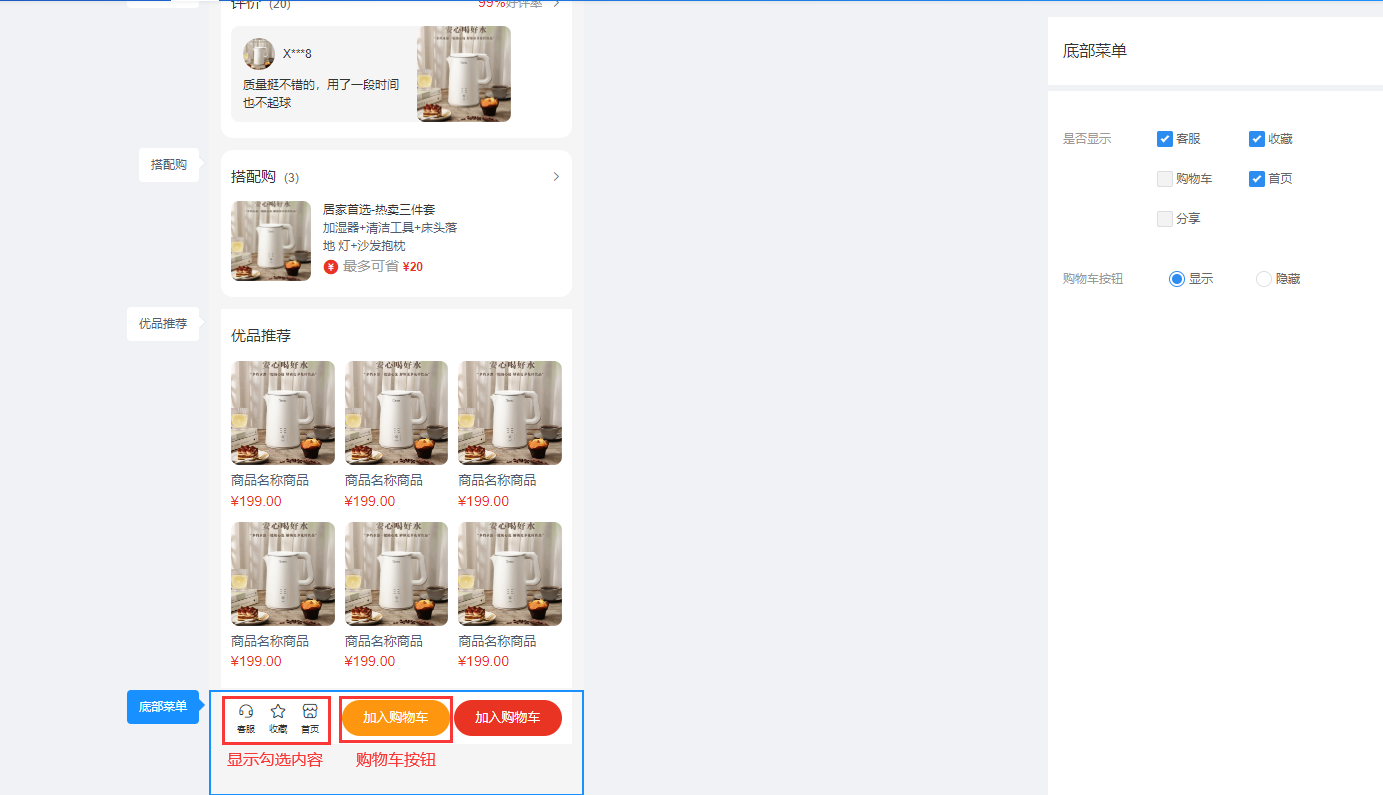
CRMEB 多店商品详情页装修说明
一、功能介绍 商家可调整商品详情各板块样式,可根据不同的需求开启或关闭单独的板块 二、操作流程 装修 > 商品详情 三、功能说明 1、商品信息 可控制商品详情页面商品信息的显示与隐藏 2、会员信息,排行榜 控制商品详情页面会员信息及排行榜的…...
Redis-使用 jedis 操作数据
文章目录 1、Jedis简介2、环境准备3、创建maven普通项目,导入如下依赖4、测试JAVA程序和Redis之间的通信 1、Jedis简介 "Jedis" 通常是作为 "Java Redis" 的缩写或简称来理解的。Java Embedded Data Structures Interface 表示 Java嵌入式数据结构接口 2、…...

简说PIP换源
概述 PIP(Python Package Installer)是 Python 的包管理工具,用于安装和管理 Python 包。默认情况下,PIP 从 Python 官方的包仓库(即 PyPI)下载和安装包。然而,由于网络原因,访问官…...

django学习入门系列之第三点《CSS基础样式介绍2》
文章目录 文字对齐方式外边距内边距往期回顾 文字对齐方式 水平对齐方式 text-align: center;垂直对齐方式 /* 注意,这个只能是一行来居中 */ line-height:/*长度*/ ;样例 <!DOCTYPE html> <html lang"en"> <head><meta charset…...

分布式光纤测温DTS在工程现场中稳定性与可靠性如何?
20年前,分布式光纤测温(Distributed Temperature Sensing,DTS)技术的发展尚不成熟,设备成本高昂,其稳定性与可靠性也存在一定问题。然而,经过二十多年的不断发展与创新,DTS技术在工程现场应用中取得了显著进…...

PHP多线程模块parallel的编译安装和多线程编程演示
从PHP7开始,多线程编原有的pthreads已经不在维护,而是使用parallel替代。 由于是新的模块,样例代码很少,这里总结一个简单的代码和详细的备注供大家参考。 编译和安装 parallel需要启用ZTS(Zend Thread Safety&…...

记录grid布局属性
grid布局 分为容器和项目元素 容器属性 #container{display:grid;grid-template-columns:100px 100px 100px;/* 1fr 表示比例为占1份 */grid-template-columns:1fr 100px 1fr;/*100px为1列,自动填充,容器宽度不足则换行*/grid-template-columns:repeat(auto-fill,100px);/* …...

12.爬虫---PyMysql安装与使用
12.PyMysql安装与使用 1.安装 PyMySQL2.使用PyMySQL2.1创建数据表2.2连接数据库2.3增加数据2.4修改数据2.5查询数据2.6删除数据2.7关闭连接 3.总结 MySQL 安装可以看这篇文章MySql 安装与使用(非常详细) 1.安装 PyMySQL PyMySQL是Python中用于连接MySQL…...
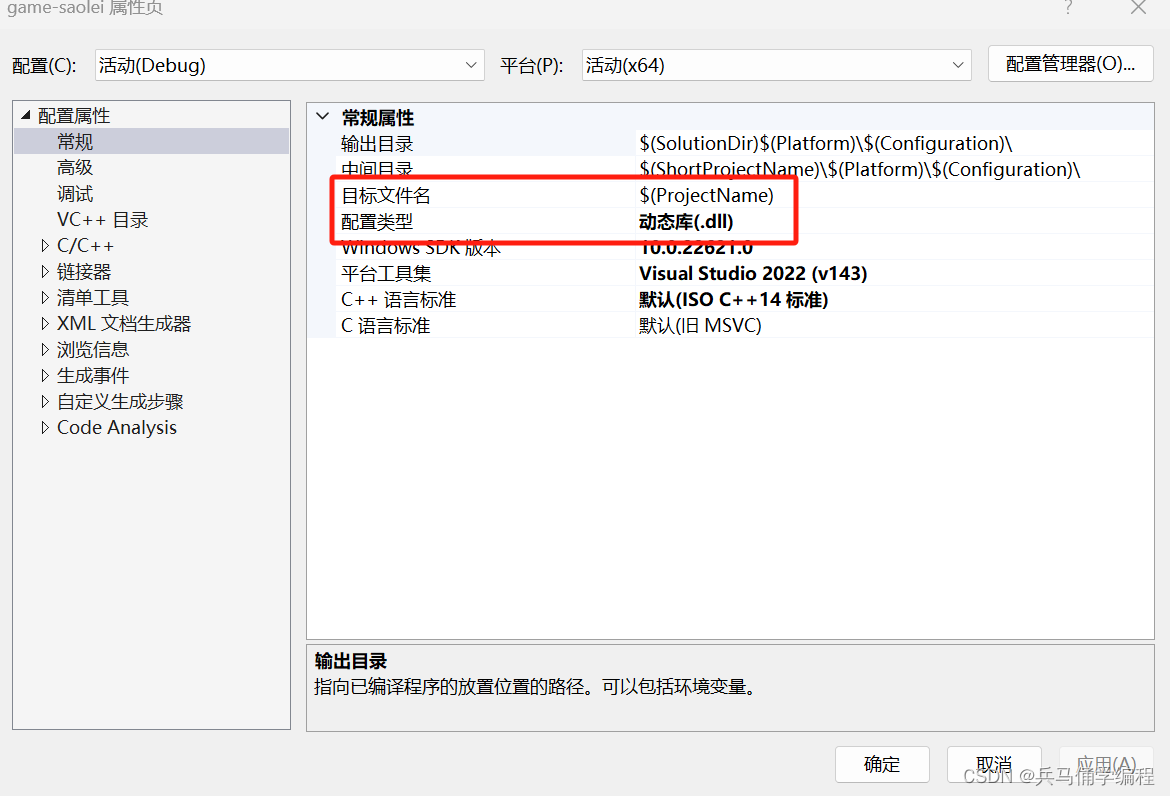
VS2022遇到的两个问题
问题一:找不到定义的头文件 别的博主说是:在属性页里面进行改写,改成是,我试过之后并不行; 解决思路:但其实在右边视图里面找到你自己定义的头文件加到你运行文件中就行;因为程序就只有一个入口…...

【Android14 ShellTransitions】(六)SyncGroup完成
这一节的内容在WMCore中,回想我们的场景,是在Launcher启动某一个App,那么参与动画的就是该App对应Task(OPEN),以及Launcher App对应的Task(TO_BACK)。在确定了动画的参与者后&#x…...

技术管理转型之战:决策之道-管理中的智慧与策略
文章目录 引言一、决策的重要性二、常见的决策方式1. 理性决策(Rational Decision Making)2. 有限理性(Bounded Rationality)3. 直觉决策(Intuitive Decision Making)4. 循证管理(Evidence-Base…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

第6章:Neo4j数据导入与导出
在实际应用中,数据的导入与导出是使用Neo4j的重要环节。无论是初始数据加载、系统迁移还是数据备份,都需要高效可靠的数据传输机制。本章将详细介绍Neo4j中的各种数据导入与导出方法,帮助读者掌握不同场景下的最佳实践。 6.1 数据导入策略 …...
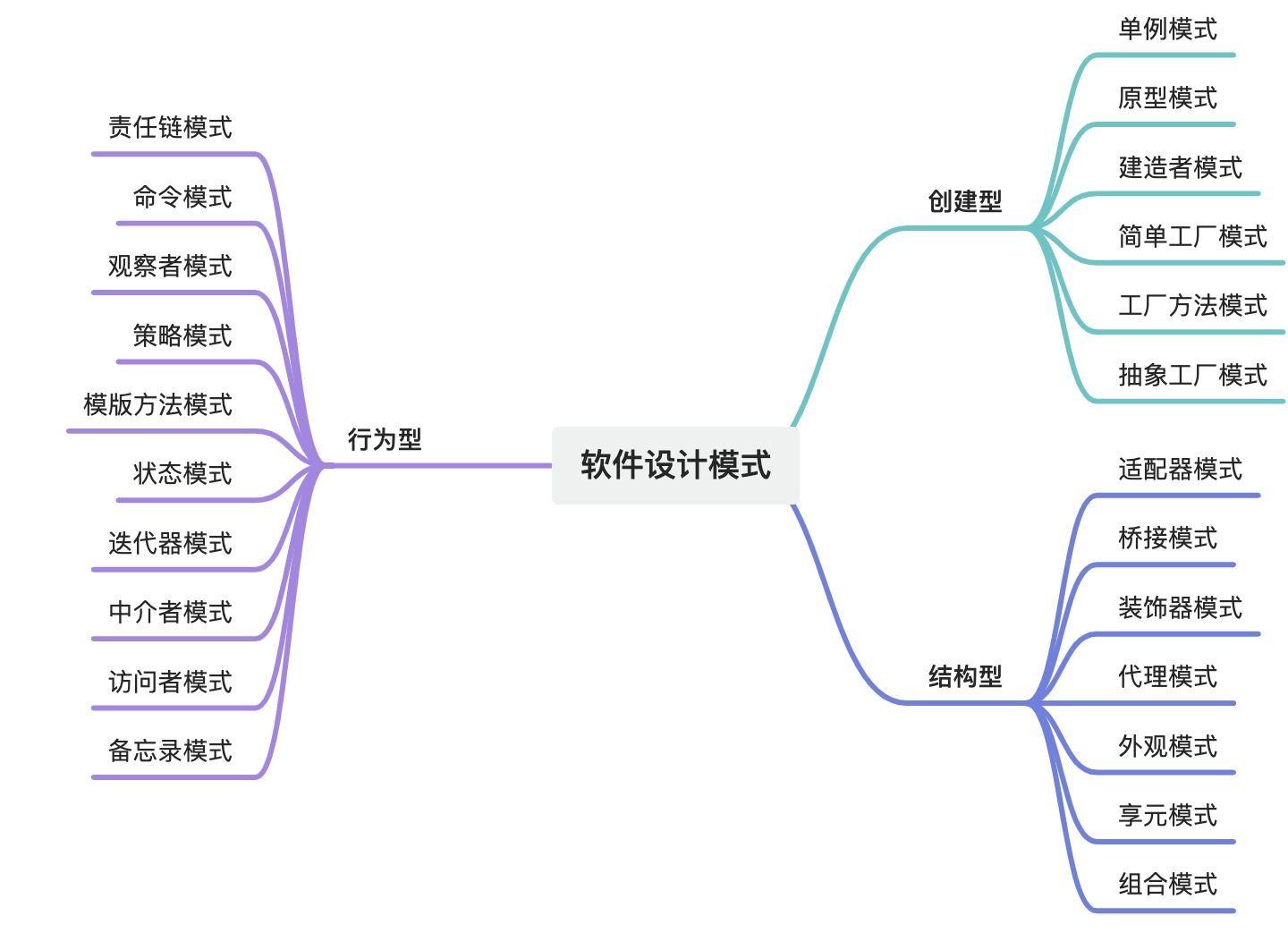
设计模式域——软件设计模式全集
摘要 软件设计模式是软件工程领域中经过验证的、可复用的解决方案,旨在解决常见的软件设计问题。它们是软件开发经验的总结,能够帮助开发人员在设计阶段快速找到合适的解决方案,提高代码的可维护性、可扩展性和可复用性。设计模式主要分为三…...
