每日一题——力扣104. 二叉树的最大深度(举一反三+思想解读+逐步优化)四千字好文

一个认为一切根源都是“自己不够强”的INTJ
![]() 个人主页:用哲学编程-CSDN博客
个人主页:用哲学编程-CSDN博客![]() 专栏:每日一题——举一反三
专栏:每日一题——举一反三
Python编程学习
Python内置函数
目录
我的写法
代码功能
代码结构
时间复杂度分析
空间复杂度分析
总结
我要更强
优化方法:迭代(使用队列)
哲学和编程思想
分治法(Divide and Conquer):
递归(Recursion):
迭代(Iteration):
抽象(Abstraction):
数据结构的选择:
空间与时间的权衡(Space-Time Tradeoff):
优化(Optimization):
实用主义(Pragmatism):
举一反三
理解问题本质:
分治法应用:
递归与迭代的转换:
抽象思维:
选择合适的数据结构:
空间与时间的权衡:
优化意识:
实用主义:
学习和模仿:
实践和反思:
Python-3.12.0文档解读
题目链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree/description/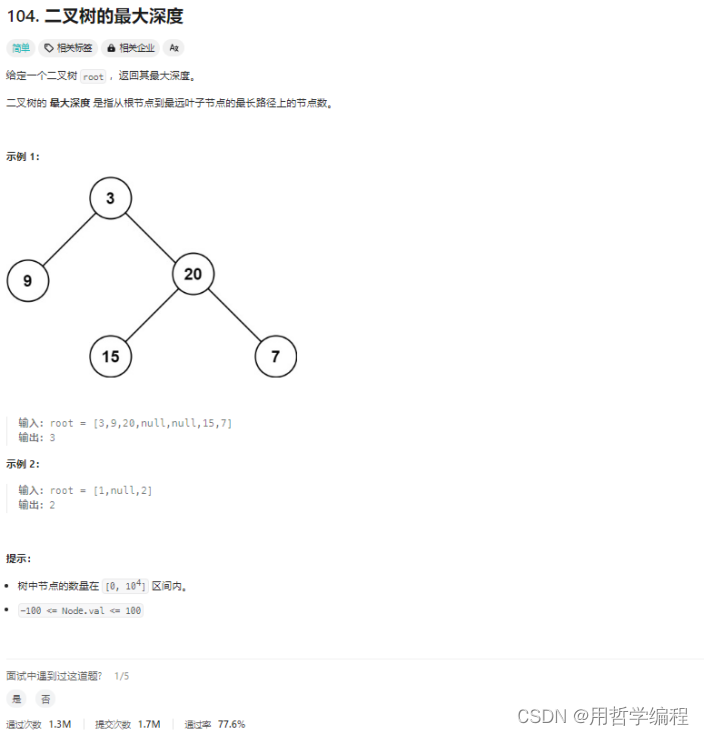
我的写法
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
int maxDepth(struct TreeNode* root) {if(!root){return 0;}else{int left_max=maxDepth(root->left);int right_max=maxDepth(root->right);return 1+(left_max>right_max?left_max:right_max);}
}
这段代码是一个用于计算二叉树最大深度的递归函数。下面是对这段代码的点评:
代码功能
代码定义了一个名为 maxDepth 的函数,它接受一个指向二叉树根节点的指针 root,并返回该二叉树的最大深度。
代码结构
- 基本情况处理:
- 如果 root 为 NULL(即树为空),则返回深度 0。
- 递归调用:
- 分别递归调用 maxDepth 函数计算左子树和右子树的最大深度,分别存储在 left_max 和 right_max 变量中。
- 结果计算:
- 通过比较 left_max 和 right_max 的大小,返回较大的值加上 1(代表当前节点)作为整棵树的最大深度。
时间复杂度分析
- 时间复杂度:O(n),其中 n 是二叉树中的节点数。每个节点仅被访问一次,因为每个节点只参与一次递归调用。
空间复杂度分析
- 空间复杂度:O(h),其中 h 是二叉树的高度。这是因为在递归调用过程中,系统栈的深度最多为树的高度。在最坏情况下(当树是一个链表时),空间复杂度为 O(n)。
总结
这段代码简洁高效,正确地实现了计算二叉树最大深度的功能。它利用递归的特性,通过比较左右子树的深度来确定当前树的最大深度,是一种典型的分治策略的应用。代码的时间复杂度为线性,空间复杂度与树的高度成正比,整体性能良好。
我要更强
在计算二叉树的最大深度时,通常情况下,上述代码已经非常高效,因为它的时间复杂度是 O(n),空间复杂度是 O(h),其中 n 是节点数,h 是树的高度。然而,如果我们考虑极端情况,例如树非常不平衡,空间复杂度可能会接近 O(n)。为了进一步优化空间复杂度,我们可以考虑使用迭代方法而不是递归,这样可以避免递归调用栈的空间开销。
优化方法:迭代(使用队列)
我们可以使用广度优先搜索(BFS)来计算树的深度,这种方法通常使用队列来实现。每次迭代处理一层的节点,从而计算出树的深度。这种方法的空间复杂度仍然是 O(w),其中 w 是树的宽度(即一层中节点最多的数量),但在最坏情况下(树非常不平衡),w 可能会接近 n,因此这种方法在空间复杂度上并没有显著优化,但它避免了递归调用栈的开销。
下面是使用队列实现的迭代方法的完整代码:
#include <stdlib.h>// 定义树节点结构
typedef struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
} TreeNode;// 定义队列节点结构
typedef struct QueueNode {TreeNode *node;struct QueueNode *next;
} QueueNode;// 定义队列结构
typedef struct Queue {QueueNode *front;QueueNode *rear;int size;
} Queue;// 初始化队列
void initQueue(Queue *q) {q->front = q->rear = NULL;q->size = 0;
}// 入队操作
void enqueue(Queue *q, TreeNode *node) {QueueNode *newNode = (QueueNode *)malloc(sizeof(QueueNode));newNode->node = node;newNode->next = NULL;if (q->rear == NULL) {q->front = q->rear = newNode;} else {q->rear->next = newNode;q->rear = newNode;}q->size++;
}// 出队操作
TreeNode *dequeue(Queue *q) {if (q->front == NULL) {return NULL;}QueueNode *temp = q->front;TreeNode *node = temp->node;q->front = q->front->next;if (q->front == NULL) {q->rear = NULL;}free(temp);q->size--;return node;
}// 计算树的最大深度
int maxDepth(TreeNode *root) {if (root == NULL) {return 0;}Queue queue;initQueue(&queue);enqueue(&queue, root);int depth = 0;while (queue.size > 0) {int levelSize = queue.size;for (int i = 0; i < levelSize; i++) {TreeNode *node = dequeue(&queue);if (node->left != NULL) {enqueue(&queue, node->left);}if (node->right != NULL) {enqueue(&queue, node->right);}}depth++;}return depth;
}这段代码通过队列实现了广度优先搜索,每次迭代处理一层的节点,从而计算出树的深度。这种方法的时间复杂度仍然是 O(n),但空间复杂度在最坏情况下可能会接近 O(n),因为它需要存储每一层的节点。在实际应用中,这种方法的性能通常与递归方法相当,但在处理大型或不平衡的树时,它可能会有更好的表现。
哲学和编程思想
上述代码和方法体现了以下哲学和编程思想:
-
分治法(Divide and Conquer):
- 递归方法中,通过将问题分解为更小的子问题(左子树和右子树的最大深度)来解决原始问题。这是一种典型的分治策略,通过解决子问题并合并结果来解决整个问题。
-
递归(Recursion):
- 递归是一种编程技巧,其中函数调用自身来解决问题。在计算树的最大深度时,递归方法通过递归地计算子树的深度来确定整个树的深度。
-
迭代(Iteration):
- 迭代是另一种编程技巧,通过循环重复执行一组操作来解决问题。使用队列的迭代方法通过遍历树的每一层来计算深度,而不是像递归那样深入到树的底部。
-
抽象(Abstraction):
- 在代码中,树节点和队列都被抽象为结构体,这有助于隐藏实现细节并提供清晰的接口。这种抽象使得代码更易于理解和维护。
-
数据结构的选择:
- 选择合适的数据结构是编程中的一个重要决策。在这里,队列被用来实现广度优先搜索,因为它允许按层处理节点,这是计算树深度的关键。
-
空间与时间的权衡(Space-Time Tradeoff):
- 递归方法使用较少的代码量,但可能会消耗较多的栈空间。迭代方法虽然代码更复杂,但避免了递归调用栈的空间开销。这种权衡是编程中常见的,需要根据具体情况选择最合适的方法。
-
优化(Optimization):
- 在编程中,优化通常意味着在时间复杂度和空间复杂度之间找到平衡。迭代方法尝试通过减少空间使用来优化递归方法,尽管在某些情况下这可能不会带来显著的改进。
-
实用主义(Pragmatism):
- 在实际编程中,选择最简单、最直接的解决方案往往是最佳实践。递归方法虽然可能消耗更多空间,但它的简洁性和直观性使其成为许多程序员的首选。迭代方法则提供了另一种选择,特别是在空间受限的情况下。
这些哲学和编程思想指导着程序员在面对问题时如何设计算法和编写代码,以实现高效、可维护和可理解的解决方案。
举一反三
根据上述哲学和编程思想,以下是一些技巧和建议,可以帮助你在编程和问题解决中举一反三:
-
理解问题本质:
- 在开始解决问题之前,深入理解问题的本质和需求。这有助于你选择合适的算法和数据结构。
-
分治法应用:
- 当面对可以分解为子问题的问题时,考虑使用分治法。例如,排序算法(如快速排序和归并排序)和搜索算法(如二分查找)都是分治法的应用。
-
递归与迭代的转换:
- 学会将递归算法转换为迭代算法,或者反之。这种转换可以帮助你理解算法的底层逻辑,并在必要时优化空间或时间复杂度。
-
抽象思维:
- 在设计数据结构和算法时,尝试抽象出问题的核心概念。这有助于你创建通用的解决方案,这些解决方案可以应用于类似的问题。
-
选择合适的数据结构:
- 根据问题的特点选择最合适的数据结构。例如,如果需要频繁插入和删除元素,链表可能是一个好选择;如果需要快速查找,数组或哈希表可能更合适。
-
空间与时间的权衡:
- 在设计算法时,始终考虑时间和空间的权衡。有时候,牺牲一些空间可以显著提高时间效率,反之亦然。
-
优化意识:
- 始终寻找改进算法性能的机会。这可能包括减少不必要的计算、使用更有效的数据结构或算法,或者利用问题的特性来简化解决方案。
-
实用主义:
- 在实际编程中,选择最简单、最直接的解决方案。复杂的解决方案可能看起来很酷,但它们往往更难以维护和理解。
-
学习和模仿:
- 研究经典算法和数据结构,理解它们的设计思想和应用场景。通过模仿这些经典解决方案,你可以学习到许多通用的编程和问题解决技巧。
-
实践和反思:
- 通过实际编写代码来解决问题,并在解决后反思你的解决方案。思考是否有更好的方法,以及如何将这些方法应用到未来的问题中。
通过将这些技巧和思想应用到实际编程和问题解决中,将能够提高编程能力,并能够更有效地解决各种问题。记住,编程不仅仅是写代码,更是一种思维方式和解决问题的艺术。
相关文章:

每日一题——力扣104. 二叉树的最大深度(举一反三+思想解读+逐步优化)四千字好文
一个认为一切根源都是“自己不够强”的INTJ 个人主页:用哲学编程-CSDN博客专栏:每日一题——举一反三Python编程学习Python内置函数 目录 我的写法 代码功能 代码结构 时间复杂度分析 空间复杂度分析 总结 我要更强 优化方法:迭代&…...

wpf textbox 有焦点 导致后台更新 前台不跟着改变
这个问题可能是由于 WPF 的数据绑定机制导致的。当 TextBox 有焦点时,它会独立于数据绑定进行更新,这可能会导致前台界面不能及时反映后台数据的变化。 1.使用 UpdateSourceTrigger 属性: 在数据绑定时,将 UpdateSourceTrigger 属性设置为 PropertyChanged。这样当 TextBox 的…...

数字化物资管理系统的未来:RFID技术的创新应用
在信息化和智能化不断发展的背景下,物资管理系统的数字化转型已成为各行各业关注的焦点。RFID技术作为一种先进的物联网技术,通过全面数字化实现物资信息的实时追踪和高效管理,为企业的物资管理提供了强有力的支持。 首先,RFID技…...

【docker】常用指令-表格整理
以下列出的指令是Docker中常用的命令,但并不是全部。Docker的指令非常丰富,可以根据具体的需求和场景选择合适的指令。同时,每个指令都有很多选项和参数可以使用,可以通过 docker COMMAND --help 来获取更详细的信息。 一、容器命…...
洛谷——P2824 排序
题目来源:[HEOI2016/TJOI2016] 排序 - 洛谷https://www.luogu.com.cn/problem/P2824 问题思路 本文介绍一种二分答案的做法,时间复杂度为:(nm)*log(n)*log(n).本题存在nlog(n)的做法,然而其做法没有二分答案的做法通俗易懂. 默认读…...

echart在线图表demo下载直接运行
echart 全面的数据可视化图表解决方案 | 折线图、柱状图、饼图、散点图、水球图等各类图表展示 持续更新中 三色带下表题速度仪表盘 地图自定义图标 动态环形图饼状图 动态水波动圆形 多标题指针仪表盘 温度仪表盘带下标题 横向柱状图排名 环形饼状图 双折线趋势变化...

MLX5_SET_TO_ONES宏解析
看代码时,遇到一个非常复杂的宏MLX5_SET_TO_ONES,这个宏的主要作用是对特定的数据结构置位,宏的上下文如下: #define __mlx5_nullp(typ) ((struct mlx5_ifc_##typ##_bits *)0) #define __mlx5_bit_off(typ, fld) (offsetof(struc…...
SQL Server入门-SSMS简单使用(2008R2版)-1
环境: win10,SQL Server 2008 R2 参考: SQL Server 新建数据库 - 菜鸟教程 https://www.cainiaoya.com/sqlserver/sql-server-create-db.html 第 2 课:编写 Transact-SQL | Microsoft Learn https://learn.microsoft.com/zh-cn/…...

高考专业抉择探索计算机专业的未来展望及适合人群
身份:一位正在面临人生重要抉择的高考生,一位计算机行业从业者 正文: 随着2024年高考落幕,我与数百万高三学生一样,又将面临人生中的重要抉择:选择大学专业。对于许多学生来说,计算机科学…...

windows安装spark
在 Windows 上安装 Spark 并进行配置需要一些步骤,包括安装必要的软件和配置环境变量。以下是详细的步骤指南: 步骤一:安装 Java 下载和安装 Java Development Kit (JDK) 到 Oracle JDK 下载页面 或 OpenJDK 下载页面 下载适合你系统的 JDK。…...
【信息学奥赛】CSP-J/S初赛03 计算机网络与编程语言分类
第1节 计算机网络基础 1.1 网络的定义 所谓计算机网络,就是利用通信线路和设备,把分布在不同地理位置上的多台计算机连 接起来。计算机网络是现代通信技术与计算机技术相结合的产物。 网络中计算机与计算机之间的通信依靠协议进行。协议是计算机收、发…...

python20 函数的定及调用
函数的定及调用 函数是将一段实现功能的完整代码,使用函数名称进行封装,通过函数名称进行调用。以此达到一次编写,多次调用的目的 用 def 关键字来声明 函数 格式: def 函数名(参数列表):函数体[:return 返回值是可选的࿰…...
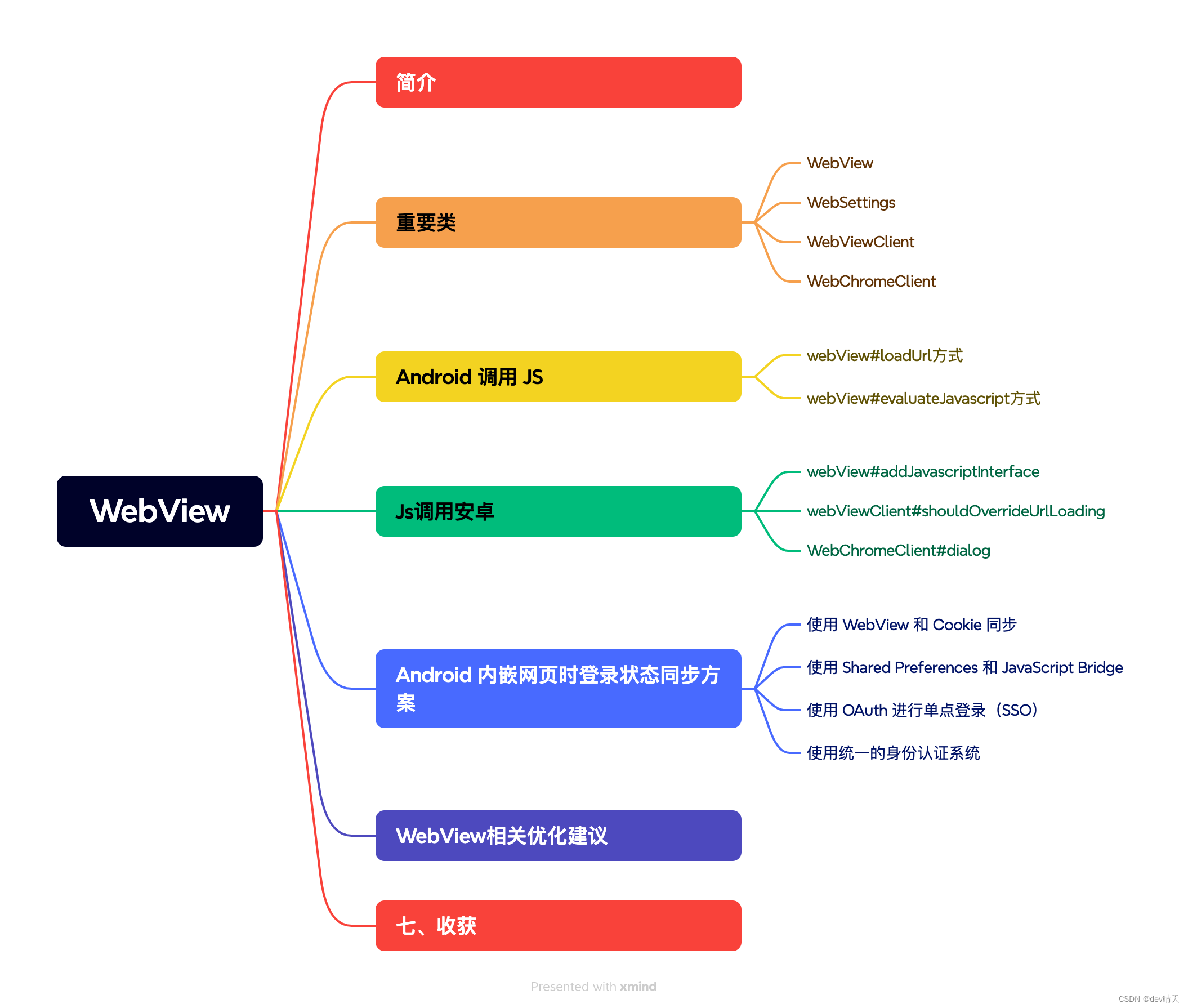
【Android WebView】WebView基础
一、简介 WebView是一个基于webkit引擎、展现web页面的控件。Android的Webview在低版本和高版本采用了不同的webkit版本内核,4.4后直接使用了Chrome。 二、重要类 以WebView类为基础,WebSettings、WebViewClient、WebChromeClient为辅助共同完成安卓段加…...
Python酷库之旅-第三方库openpyxl(03)
目录 一、 openpyxl库的由来 1、背景 2、起源 3、发展 4、特点 4-1、支持.xlsx格式 4-2、读写Excel文件 4-3、操作单元格 4-4、创建和修改工作表 4-5、样式设置 4-6、图表和公式 4-7、支持数字和日期格式 二、openpyxl库的优缺点 1、优点 1-1、支持现代Excel格式…...
电脑丢失dll文件一键修复的方法有哪些?分析dll文件修复的多种策略
我们经常会遇到各种各样的问题,其中之一就是DLL文件的丢失。DLL文件(动态链接库)是操作系统和应用程序正常运行所必需的文件,当这些文件丢失或损坏时,可能会导致软件无法正常启动,甚至影响系统的稳定性。对…...

小程序项目业务逻辑回忆4
用户查询积分 积分获取规则如下: 邀请其他用户购票参会,将获取该用户花费金额的10%获取积分。 邀请用户注册参观展览,需注册并现场签到,将获取10分的奖励积分。 邀请企业用户参展,将获取企业参展金额的5%获取到积分。 上述3条积分获取规…...
)
LeetCode 16.最接近的三数之和(C++)
链接 https://leetcode.cn/problems/3sum-closest/description/ 题目 给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。 返回这三个数的和。 假定每组输入只存在恰好一个解。 示例1 输入&a…...

JSON.parse 解析NaN, Infinity, -Infinity失败
背景 JSON.parse() 方法解析字符串时, 如果字符串包含NaN, Infinity, -Infinity会报错。因为我们需要先将NaN, Infinity, -Infinity替换成字符类型,再做转换 解决方法 function convert(str) {str str.replace(/NaN/g, "NaN");str str.re…...

【计算机】我不允许还有人不知道数据库是什么
数据库是计算机科学中的一个核心概念,它是用于存储、检索、管理和处理数据的系统。在现代的软件开发和信息技术中,数据库扮演着至关重要的角色。以下是关于数据库的一些基本要点: 数据存储: 数据库提供了一个结构化的方式来存储数据,使得数据可以高效地组织和访问。它通过…...
制作WIFI二维码,实现一键扫描连接WIFI
在现代社会,Wi-Fi已成为我们日常生活中不可或缺的一部分。无论是在家庭、办公室还是公共场所,我们都希望能够快速方便地连接到Wi-Fi网络。下面小编就来和大家分享通过制作WIFI二维码,来实现一键扫描就可以连接WIFI的方法。连接WIFI不用在告诉…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
