打印水仙花数
题目:打印出所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字立方和等于该数本身。
例如:153是一个“水仙花数”,因为153 = 1的三次方
+5的三次方+3的三次方。
程序分析:利用for循环控制100 - 999个数,每个数分解出个位,十位,百位。
void main()
{int i, j, k, n;printf("'water flower'number is:");for (n = 100; n < 1000; n++){i = n / 100;/*分解出百位*/j = n / 10 % 10;/*分解出十位*/k = n % 10;/*分解出个位*/if (i * 100 + j * 10 + k == i * i * i + j * j * j + k * k * k) //判断条件简单易懂{printf("%-5d", n);}}printf("\n");
}
相关文章:

打印水仙花数
题目:打印出所有的“水仙花数”,所谓“水仙花数”是指一个三位数,其各位数字立方和等于该数本身。 例如:153是一个“水仙花数”,因为153 1的三次方 +5的三次方+3的三次方。 程序分析ÿ…...

【SCAU数据挖掘】数据挖掘期末总复习题库简答题及解析——下
1.从某超市顾客中随机抽取5名,他们的购物篮数据的二元0/1表示如下: 顾客号 面包 牛奶 尿布 啤酒 鸡蛋 可乐 1 1 1 0 0 0 0 2 1 0 1 1 1 0 3 0 1 1 1 0 1 4 1 1 1 1 0 0 5 1 1 1 0 0 1 某学生依据这些数据做…...

PyQt学习之简介
1.Python图形界面称为程序的用户交互界面,英文称之为 UI (user interface) Tkinter 基于Tk的Python库,Python官方采用的标准库,优点是作为Python标准库、稳定、发布程序较小,缺点是控件相对较少。 wxPython 基于wxWidgets的Py…...

深入理解前端缓存
前端缓存是所有前端程序员在成长历程中必须要面临的问题,它会让我们的项目得到非常大的优化提升,同样也会带来一些其它方面的困扰。大部分前端程序员也了解一些缓存相关的知识,比如:强缓存、协商缓存、cookie等,但是我…...

K-means聚类算法详解与实战
一、引言 K-means聚类算法是一种无监督学习算法,旨在将数据点划分为K个不同的聚类或群组,使得同一聚类内的数据点尽可能相似,而不同聚类间的数据点尽可能不同。在图像处理、数据挖掘、客户细分等领域有着广泛的应用。本文将通过图文结合的方…...

python数据分析-糖尿病数据集数据分析预测
一、研究背景和意义 糖尿病是美国最普遍的慢性病之一,每年影响数百万美国人,并对经济造成重大的经济负担。糖尿病是一种严重的慢性疾病,其中个体失去有效调节血液中葡萄糖水平的能力,并可能导致生活质量和预期寿命下降。。。。 …...

【前端】 nvm安装管理多版本node、 npm install失败解决方式
【问题】If you believe this might be a permissions issue, please double-check the npm ERR! permissio或者Error: EPERM: operation not permitted, VScode中npm install或cnpm install报错 简单总结,我们运行npm install 无法安装吧包,提示权限问题…...

第11天:API开发与REST framework
第11天:API开发与REST framework 目标 使用Django REST framework构建RESTful API。 任务概览 学习序列化器的概念和使用方法。创建API视图和路由。实现API的权限和认证。 详细步骤 1. 学习序列化器 序列化器是Django REST framework中用于数据转换的组件&am…...

2024 年解锁 Android 手机的 7 种简便方法
您是否忘记了 Android 手机的 Android 锁屏密码,并且您的手机已被锁定?您需要使用锁屏解锁 Android 手机?别担心,您不是唯一一个忘记密码的人。我将向您展示如何解锁 Android 手机的锁屏。 密码 PIN 可保护您的 Android 手机和 G…...

利用机器学习重构视频中的人脸
引言 中国与英国的研究团队携手合作,开创了一种创新的视频面孔重塑技术。这项技术能够以极高的一致性对视频中的面部结构进行逼真的放大和缩小,且避免了常见伪影的产生。 从研究人员选取的YouTube视频样例中可见,经过处理后,女演…...

2021数学建模C题目– 生产企业原材料的订购与运输
C 题——生产企业原材料的订购与运输 思路:该题主要是通过对供应商的供货能力和运送商的运货能力进行估计,给出合适的材料订购方案 程序获取 第一题问题思路与结果: 对 402 家供应商的供货特征进行量化分析,建立反映保障企业生…...

C# OpenCvSharp 图像复制-clone、copyTo
在C#中使用OpenCvSharp库处理图像时,clone和copyTo是两个非常常用的函数。理解和合理使用这些函数可以帮助你在图像处理项目中更高效地操作图像数据。本文将详细介绍这两个函数的使用方法,并通过具体的示例来说明它们的实际应用。 1. clone 函数 定义 …...

中国投入到终止遗传性疾病的战斗
中国投入到终止遗传性疾病的战斗 编译 李升伟 于2006年6月在澳大利亚的墨尔本会议上启动的人类变异组计划(Human Variome Project,简称HVP),旨在全球范围内广泛收集所有基因和蛋白质序列变异和多态性的数据,采用全基…...

PCL common中常见的基础功能函数
文章目录 一、common模块中的头文件二、common模块中的基本函数1、angles.h2、centroid.h1)计算给定一群点的3D中心点,并且返回一个三维向量2)计算给定的三维点云的协方差矩阵。3)计算正则化的3*3的协方差矩阵以及给定点云数据的中心点4)利用一组点的指数对其进行一般的、…...

力扣每日一题 6/22 字符串/贪心
博客主页:誓则盟约系列专栏:IT竞赛 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 2663.字典序最小的美丽字符串【困难】 题目: 如果一个字符串满…...

MCT Self-Refine:创新集成蒙特卡洛树搜索 (MCTS)提高复杂数学推理任务的性能,超GPT4,使用 LLaMa-3 8B 进行自我优化
📜 文献卡 题目: Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B作者: Di Zhang; Xiaoshui Huang; Dongzhan Zhou; Yuqiang Li; Wanli OuyangDOI: 10.48550/arXiv.2406.07394摘要: This pape…...
自制HTML5游戏《开心消消乐》
1. 引言 游戏介绍 《开心消消乐》是一款基于HTML5技术开发的网页游戏,以其简单的操作方式、轻松的游戏体验和高度的互动性,迅速在社交平台上获得了广泛的关注和传播。玩家通过消除相同类型的元素来获得分数,游戏设计巧妙,易于上手…...
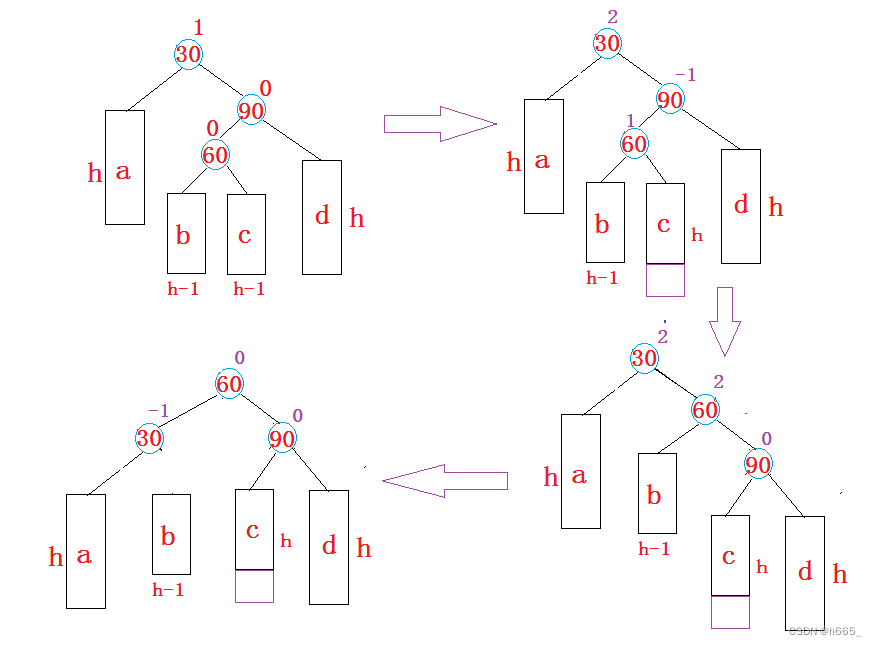
【C++】平衡二叉树(AVL树)的实现
目录 一、AVL树的概念二、AVL树的实现1、AVL树的定义2. 平衡二叉树的插入2.1 按照二叉排序树的方式插入并更新平衡因子2.2 AVL树的旋转2.2.1 新节点插入较高左子树的左侧(LL平衡旋转)2.2.2 新节点插入较高右子树的右侧(RR平衡旋转)…...

第一百一十八节 Java面向对象设计 - Java接口
Java面向对象设计 - Java接口 什么是接口? Java中的接口定义了一个引用类型来创建抽象概念。接口由类实现以提供概念的实现。 在Java 8之前,一个接口只能包含抽象方法。 Java 8允许接口具有实现的静态和默认方法。 接口通过抽象概念定义不相关类之间…...

Flink nc -l -p 监听端口测试
1、9999端口未占用 netstat -apn|grep 99992、消息发送端 nc -l -k -p 9999 {"user":"ming","url":"www.baidu1.com", "timestamp":1200L, "score":1} {"user":"xiaohu","url":…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
