动态规划:基本概念
Dynamic Programming
动态规划(Dynamic Programming, DP) 是一种算法设计技巧,通常用来解决具有重叠子问题和最优子结构性质的问题。它通过将问题分解为更小的子问题,逐步解决这些子问题并将结果存储起来,以避免重复计算,从而提高效率。
1. 特点
1.1 重叠子问题
在许多递归问题中,计算过程中会多次遇到相同的子问题。如果我们每次遇到这些子问题时都重新计算,会导致大量的重复计算和效率低下。重叠子问题的思想是通过将子问题的结果存储起来,避免重复计算,从而提高效率。
举例
斐波那契数列
递归关系式
T ( n ) = T ( n − 1 ) + T ( n − 2 ) T(n)=T(n-1)+T(n-2) T(n)=T(n−1)+T(n−2)
计算T(3)
T ( 3 ) = T ( 2 ) + T ( 1 ) = T ( 1 ) + T ( 0 ) + T ( 1 ) \begin{aligned} T(3) &= T(2) + T(1) \\ &= T(1) + T(0) + T(1) \end{aligned} T(3)=T(2)+T(1)=T(1)+T(0)+T(1)
这里我们可以看见T(1)被多次计算
这个多次计算的T(1)便被称为重复子问题
如果我们用递归来解决这个问题
int fin(int n){if(n==1)return 1;if(n==0)return 0;return fin(n-1)+fin(n-2);
}
画出递归树
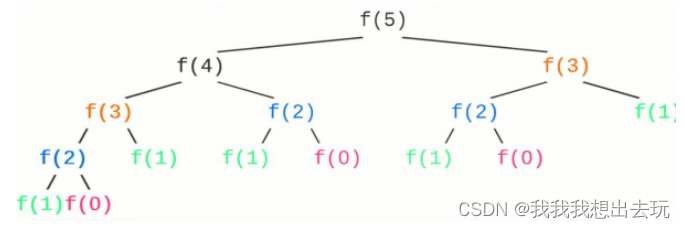
我们可以看到有多次递归调用都是重复的,即出现了重复子问题。
1.2 记忆化存储
继续探究斐波那契问题
我们之前发现使用递归解决问题时出现了多次递归调用是重复的
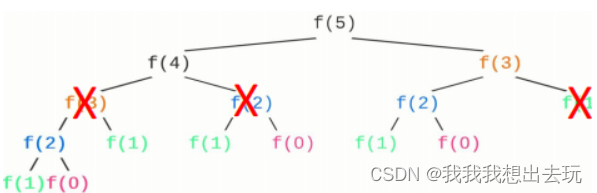
我们可以将这些重复子问题的结果储存起来,这样下一次需要解决这个子问题的时候,只需要访问之前的结果就可以了。
模拟实现
int fin(int n){std::vector<int>Fin(n+1);Fin[0]=0;Fin[1]=1;for(int i=2;i<=n;i++){Fin[i]=Fin[i-1]+Fin[i-2];}return Fin[n];
}
可以看出来我们是从最小子问题来逐渐递推至最后的答案,这也被称为自底而上的算法
1.4 状态转移方程
我们来看斐波那契数列的递推关系式
T ( n ) = T ( n − 1 ) + T ( n − 2 ) T(n)=T(n-1)+T(n-2) T(n)=T(n−1)+T(n−2)
这里我们可以看出,如果我们想得到第n项的答案,我们就要知道第n-1项和第n-2项的答案
T ( n ) ← 这个第 n 项的答案,就定义为一个状态 T(n) \gets 这个第n项的答案,就定义为一个状态 T(n)←这个第n项的答案,就定义为一个状态
状态转移方程表示的就是某一个状态和其他状态之间的关系
T ( n ) = T ( n − 1 ) + T ( n − 2 ) T(n)=T(n-1)+T(n-2) T(n)=T(n−1)+T(n−2)
这个方程就表示第n个状态是由第n-1个状态和第n-2个状态决定
1.5 最优子结构
还是看斐波那契数列
我们如果要求出第n个状态的状态值,那么我们一定是使用第n-1个状态和第n-2个状态的值来计算的。
由于我们的状态转移方程是确定的,这里求出的一定是最优解。
给出定义
如果一个问题的最优解包含了其子问题的最优解,则称这个问题具有最优子结构性质。
2. 用动态规划来设计算法的步骤
2.1 理解问题并确定子问题
首先,理解斐波那契数列的问题。斐波那契数列定义如下:
F ( n ) = F ( n − 1 ) + F ( n − 2 ) F(n) = F(n-1) + F(n-2) F(n)=F(n−1)+F(n−2)
其初始条件为:
F ( 0 ) = 0 F(0) = 0 F(0)=0
F ( 1 ) = 1 F(1) = 1 F(1)=1
这个问题可以分解为子问题,即计算第 ( n ) 项的值依赖于第 ( n-1 ) 项和第 ( n-2 ) 项的值。
2.2 定义状态
定义状态 ( dp[i] ) 表示斐波那契数列第 ( i ) 项的值。
d p [ i ] ← 斐波那契数列第 i 项的值 dp[i] \gets 斐波那契数列第 i 项的值 dp[i]←斐波那契数列第i项的值
2.3 确定状态转移方程
状态转移方程基于斐波那契数列的递归定义,可以写作:
d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i] = dp[i-1] + dp[i-2] dp[i]=dp[i−1]+dp[i−2]
2.4 确定初始状态和边界
根据斐波那契数列的初始条件,初始化状态:
d p [ 0 ] = 0 dp[0] = 0 dp[0]=0
d p [ 1 ] = 1 dp[1] = 1 dp[1]=1
2.5 利用状态转移方程计算状态值
使用状态转移方程从初始状态开始逐步计算到目标状态值。
#include <vector>int fib(int n) {if (n <= 1) return n;std::vector<int> dp(n + 1);dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; ++i) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}
相关文章:

动态规划:基本概念
Dynamic Programming 动态规划(Dynamic Programming, DP) 是一种算法设计技巧,通常用来解决具有重叠子问题和最优子结构性质的问题。它通过将问题分解为更小的子问题,逐步解决这些子问题并将结果存储起来,以避免重复计…...

小山菌_代码随想录算法训练营第二十九天| 455. 分发饼干 、376. 摆动序列、53. 最大子序和
455. 分发饼干 文档讲解:代码随想录.分发饼干 视频讲解:贪心算法,你想先喂哪个小孩?| LeetCode:455.分发饼干 状态:已完成 代码实现 class Solution { public:int findContentChildren(vector<int>&…...

快手可灵大模型开放视频续写功能,可生成最长约3分钟视频
6月21日,可灵再度进化,正式推出图生视频功能,支持用任意静态图像生成5s视频,并且可搭配不同的文本内容,实现丰富的视觉叙事 。 同时,可灵还发布了业内领先的视频续写功能,可为已生成的视频&…...

【代码随想录】【算法训练营】【第45天】 [198]打家劫舍 [213]打家劫舍II [337]打家劫舍III
前言 思路及算法思维,指路 代码随想录。 题目来自 LeetCode。 day 45,周五,坚持不了一点~ 题目详情 [198] 打家劫舍 题目描述 198 打家劫舍 解题思路 前提: 思路: 重点: 代码实现 C语言 虚拟头…...
python安装目录文件说明----Dlls文件夹
在Python的安装目录下,通常会有一个DLLs文件夹,它是Python标准库的一部分。这个文件夹包含了一些动态链接库(Dynamic Link Libraries,DLL),这些库提供了Python解释器和标准库的一些关键功能。以下是对这个文…...

java实现持续集成
要使用Java实现Jenkins持续集成,你可以使用Jenkins的Java客户端库来执行一些常见的操作,例如创建任务,触发构建等。下面是一个简单的示例代码,展示了如何使用Java实现Jenkins持续集成: java import com.offbytwo.jenk…...

ClickHouse安装与下载22.3.2.2
ClickHouse安装与下载 目录 1. ClickHouse简介 1.1 ClickHouse优点: 1.2 ClickHouse缺点: 1.3 ClickHouse引擎: 1.3.1 数据库引擎 1.3.2 表引擎 2. ClickHouse下载安装 2.1 ClickHouse下载安装 2.2 ClickHouse使用 1. ClickHouse简…...

【Go语言】Gin 框架教程
Gin 框架教程 1.第一个 Gin 程序 1.1 Gin 安装 # 执行执行如下操作即可,安装Gin前需要安装Go环境 go get -u -v github.com/gin-gonic/gin # -v:打印出被构建的代码包的名字 # -u:已存在相关的代码包,强行更新代码包及其依赖包…...
MySQL性能问题诊断方法和常用工具
作者介绍:老苏,10余年DBA工作运维经验,擅长Oracle、MySQL、PG数据库运维(如安装迁移,性能优化、故障应急处理等) 公众号:老苏畅谈运维 欢迎关注本人公众号,更多精彩与您分享。MySQL运…...

CGFloat转NSString保持原有的精度,末尾不添加0
问题阐述: 我们进行CGFloat转NSString可能会遇到一个问题 例如有一个CGFloat的值为2.1,转化成NSString后显示2.1000... 解决办法: 方法一: 如何解决呢,可以使用%g格式符,可以保证传入的不管是2还是2.1…...

UDS服务——TransferData (0x36)
诊断协议那些事儿 诊断协议那些事儿专栏系列文章,本文介绍TransferData (0x36)—— 数据传输,用于下载/上传数据时用的,数据的传输方向由不同的服务控制:0x34服务表示下载,0x35服务表示上传。通过阅读本文,希望能对你有所帮助。 文章目录 诊断协议那些事儿传输数据服务…...

jQuery 基本操作
01-简介 jQuery 是一个功能丰富且广泛使用的 JavaScript 库,它简化了 HTML 文档遍历和操作、事件处理、动画和 Ajax 操作。jQuery 通过其易用的 API,使复杂的 JavaScript 编程任务变得更加简单,并且兼容各种浏览器。 1、jQuery特点 简化 DOM …...

有玩家在2011年的MacBook上成功运行了Windows XP 还安装了触摸屏
我们已经在许多不同的设备上看到过 Windows XP 正在运行。这个古老的操作系统于 2001 年正式推出,现在已经老到其最后一次软件更新是在近十年前。一位好奇的玩家试图在 2011 年的触摸屏 MacBook 上为 Windows XP 打造了一个新家,复古技术探索者 Michael …...

高纯PFA容量瓶PFA试剂瓶在半导体材料的应用
在半导体生产过程中,为避免金属污染对硅器件性能造成不利影响,碳化硅产业链不同阶段产品(如衬底、外延、芯片、器件)表面的痕量杂质元素浓度表征至关重要。 在实验人员使用质谱法高精度检测第三代半导体碳化硅材料的痕量杂质浓度…...
AudioSep:从音频中分离出特定声音(人声、笑声、噪音、乐器等)本地一键整合包下载
AudioSep是一种 AI 模型,可以使用自然语言查询进行声音分离。这一创新性的模型由Audio-AGI开发,使用户能够通过简单的语言描述来分离各种声音源。 比如在嘈杂的人流车流中说话的录音中,可以分别提取干净的人声说话声音和嘈杂的人流车流噪声。…...

Prompt 提示词工程:翻译提示
近期在对计算机学习时,许多内容需要看原始的英文论文,对于我这种学渣来说特别不友好,🤷🏻♀️无奈只能一边看翻译,一边学习。 之前有搜到过专门的翻译工具,无奈都是按照字数算费用的…...

【MySQL 的三大日志的作用】
在管理MySQL数据库时,了解和区分数据库使用的三大日志类型至关重要。这些日志对于确保数据的完整性、提供恢复机制以及维持数据库的稳定性发挥着关键作用。最主要还是小豆前段时间去参加面试被问到了这些内容,下面将详细讨论Redo Log、Binlog和Undo Log的…...

数据库中数据的id生成和算法
id生成策略 自增主键 一般使用整数类型的id可使用自增主键的策略去生成id 优点: 简单、易于使用和理解。保证唯一性,无需额外的查询操作。提高查询性能,因为ID是有序的,且支持索引。 缺点: 不适用于分布式系统&a…...

SystemVerilog Assertion精华知识
前言 断言主要用于验证设计的行为。断言也可用于提供功能覆盖率,并标记用于验证的输入激励不符合假定的需求。 在验证平台中,通常进行三个主要任务: 产生激励功能检查功能覆盖率度量 在当今的设计越来越复杂情况下,像波形调试…...
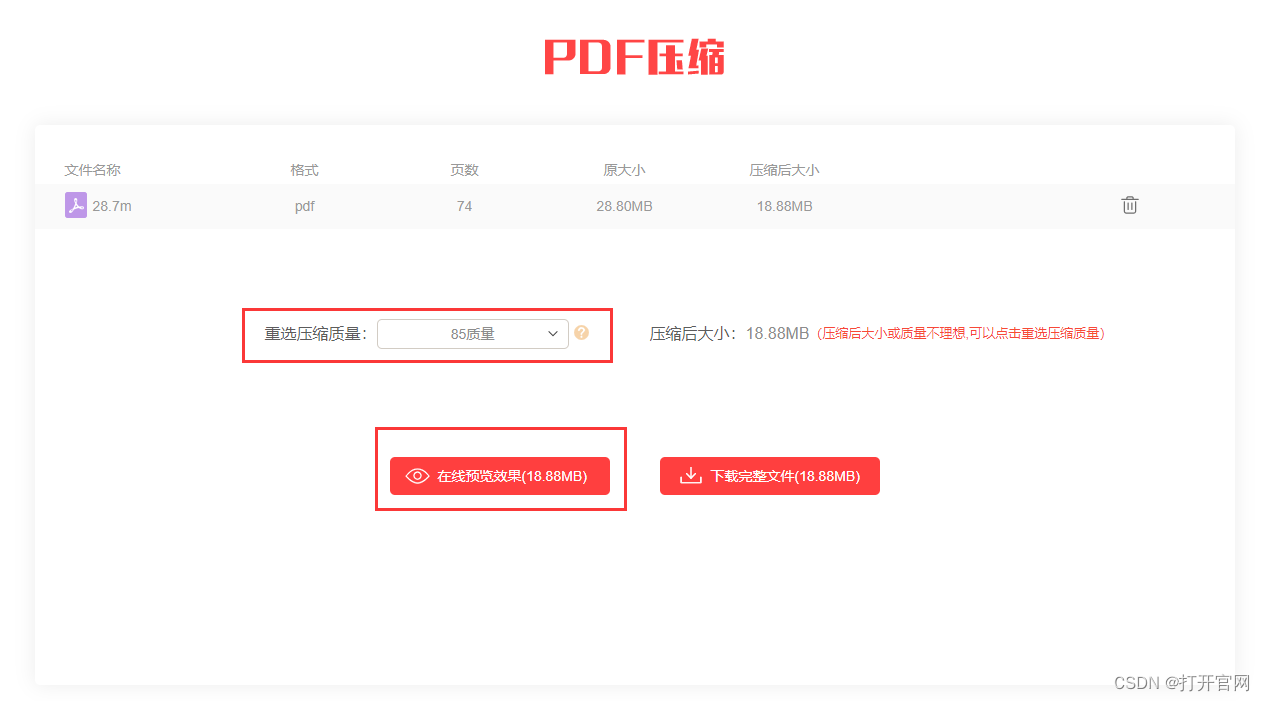
pdf怎么压缩到2m以内或5m以内的方法
PDF作为一种广泛使用的文档格式,已经成为我们工作和生活中不可或缺的一部分。然而,有时候PDF文件内存会比较大,给我们的存储和传输带来了很大的不便。因此,学会压缩 PDF 文件是非常必要的。 打开"轻云处理pdf官网"&…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
