Java比较运算符
关系运算符和比较运算符适用于条件判断类型。
相当于布尔值,只有True和False两个
符号 说明
== a==b,判断a的值是否等于b的值,条件成立为true,不成立为false
!= a!=b,判断a和b的值是否不相等,条件成立为true,不成立为false
> a>b,判断a的值是否大于b的值,条件成立为true,不成立为false
< a<b,判断a的值是否小于b的值,条件成立为true,不成立为false
>= a>=b,判断a的值是否大于等于b的值,条件成立为true,不成立为false
<= a<=b,判断a的值是否小于等于b的值,条件成立为true,不成立为false原文链接: Java比较运算符 - 红客网络编程与渗透技术

原文链接: Java比较运算符 - 红客网络编程与渗透技术
例如:
public class panduan {public static void main(String[] args) {int a = 10;int b = 10;//利用if else语句判断a跟b的关系是否成立if (a == b){System.out.println("条件成立");//条件成立为true}else {System.out.println("条件不成立");//条件不成立为false}}
}原文链接: Java比较运算符 - 红客网络编程与渗透技术
相关文章:

Java比较运算符
关系运算符和比较运算符适用于条件判断类型。 相当于布尔值,只有True和False两个 符号 说明ab,判断a的值是否等于b的值,条件成立为true,不成立为false ! a!b,判断a和b的值是否不相等,条件成立为true,不成立为false > …...
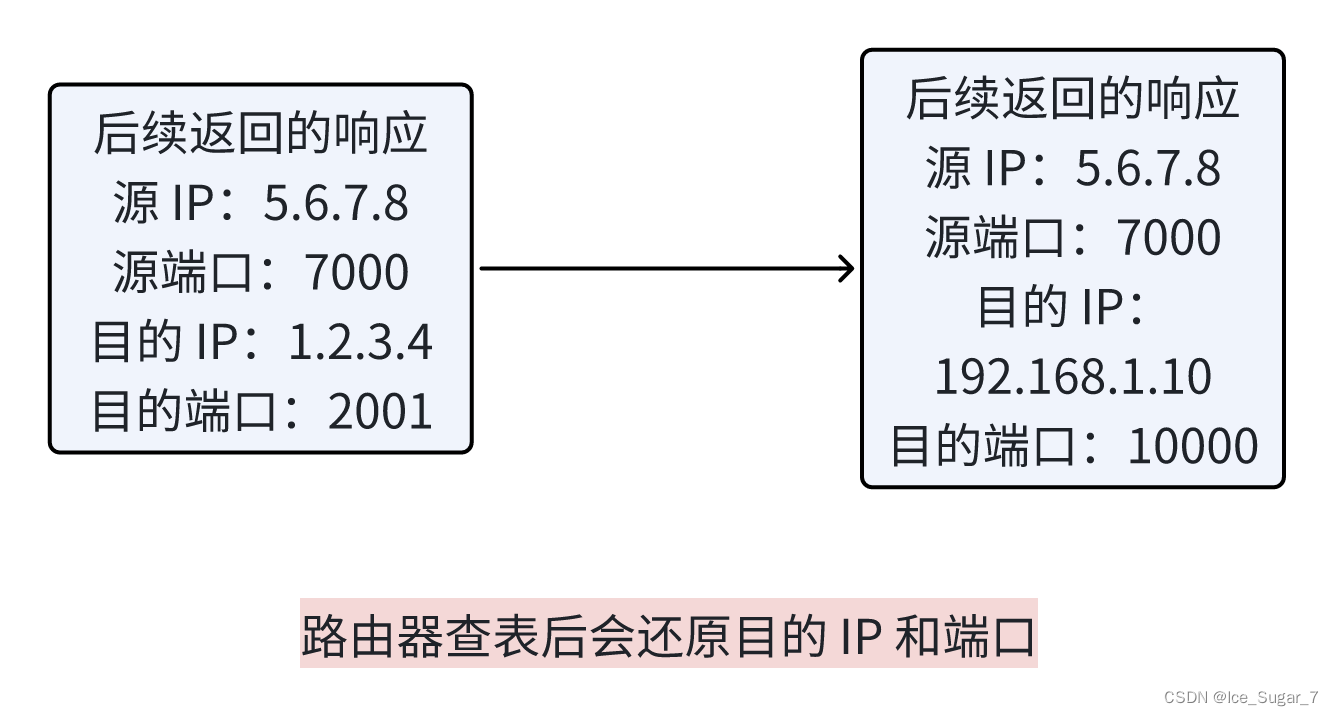
「网络原理」IP 协议
🎇个人主页:Ice_Sugar_7 🎇所属专栏:计网 🎇欢迎点赞收藏加关注哦! IP 协议 🍉报头结构🍉地址管理🍌动态分配 IP 地址🍌NAT 机制(网络地址映射&am…...

电商平台生活用品销售数据分析与应用
摘 要 在当前互联网飞速发展的时代,计算机应用给我们的工作生活带来了极大的便利。如今我们的生活离不开电商平台,其随之而来的是各种各样的销售数据与消费者信息,这些数据和信息的分析应用成为了当前互联网领域研究的重要部分。 本论文以基…...

FastAdmin数据库设计规范
FastAdmin数据库设计规范,官方文档上也有,仅仅是为了我自己做一次笔记增加记忆强度 表名和字段名全小写,只允许出现a-z和_这几种字符,且不能有拼音,只能为英文单词存储引擎统一使用innodb引擎字符集统一使用utf8mb4,排序规则使用…...
基于MATLAB仿真LFM线性调频信号
基于MATLAB仿真LFM线性调频信号 目录 前言 一、LFM信号简介 二、LFM信号基本原理 三、LFM信号仿真 四、代码 总结 前言 仿真中的接收信号,有时为了简单会直接用一个正弦波代替,但实际中接收到的信号极少是点频信号,一般都是PSK信号、OF…...

互联网的盈利模式
1. 广告收入 展示广告:通过在网站或应用上展示横幅广告、视频广告等,按点击次数(CPC)或展示次数(CPM)收费。搜索广告:通过搜索引擎上的关键词竞价广告,按点击次数收费。社交媒体广告…...

什么是距离选通型水下三维激光扫描仪?(下)
距离选通激光水下成像的发展 距离选通激光成像技术始于上世纪60年代,受制于高性能脉冲激光器和选通成像器件发展的制约,激光距离选通成像技术在随后的二十年发展缓慢,直到20世纪90年代,随着硬件技术的不断成熟,该技术…...

计算机网络(谢希仁第六版)| 课后习题与答案 | 物理层 | 题目知识点详细分析
计算机网络(谢希仁第六版)课后习题与答案 物理层 博客只对老师给的重点进行整理,完整的课后习题答案见Gitee下载:《计算机网络教程(第6版)(微课版)》习题答案 2-5 请画出数据流1 0 1…...

安卓安装linux + .net环境
安装Termux 到下面地址获取apk安装包 https://github.com/termux/termux-app 安装ssh ~ $ pkg install openssl ~ $ pkg install openssh查看用户名 ~ $ whoami ssh u0_a390修改当前用户密码 passwd 启动ssh sshd 安装 proot-distro pkg install proot-distro 列出能装的lin…...

ES6 新增Set 和 Map 两种数据结构
ES6 新增了 Set 和 Map 这两种数据结构,它们为 JavaScript 提供了更强大和灵活的数据处理能力。下面详细介绍一下 Set 和 Map 的特性和用法: Set Set 是一种类似于数组的数据结构,但是成员的值都是唯一的,没有重复的值。 特性&…...
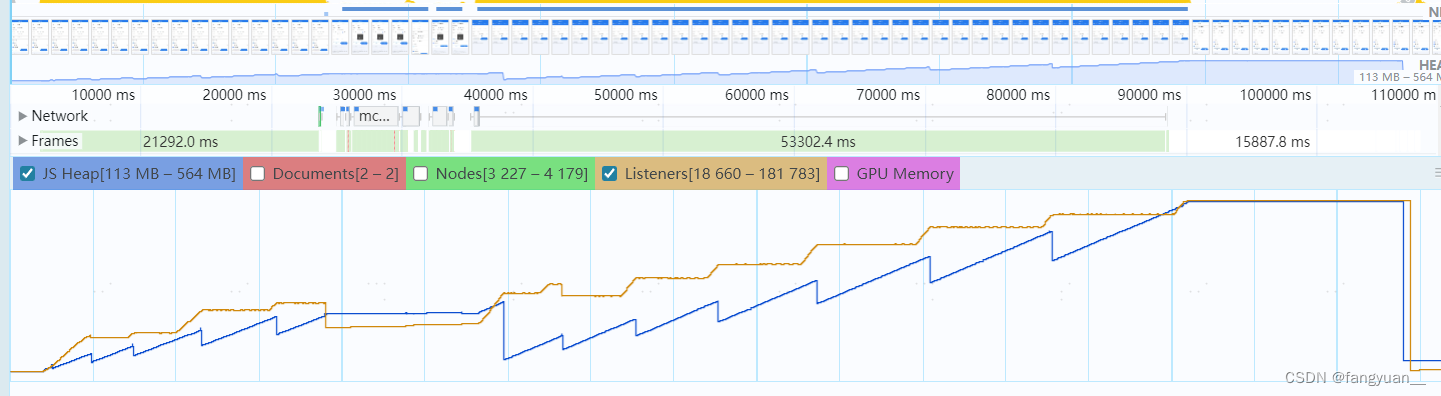
【学一点儿前端】单页面点击前进或后退按钮导致的内存泄露问题(history.listen监听器清除)
今天测试分配了一个比较奇怪的问题,在单页面应用中,反复点击“上一步”和“下一步”按钮时,界面表现出逐渐变得卡顿。为分析这一问题,我用Chrome的性能监控工具进行了浏览器性能录制。结果显示,每次点击“上一步”按钮…...

vue跳转页面 如果登录了直接跳转 没有登录登录完以后直接跳转,使用vuex管理登录状态
在Vue.js中,如果你需要在用户登录后重定向到他们原本想要访问的页面,你可以使用Vue Router的beforeEach守卫来实现这个功能。以下是实现这一需求的步骤: 存储目标路由:在用户被重定向到登录页面之前,存储他们想要访问的…...
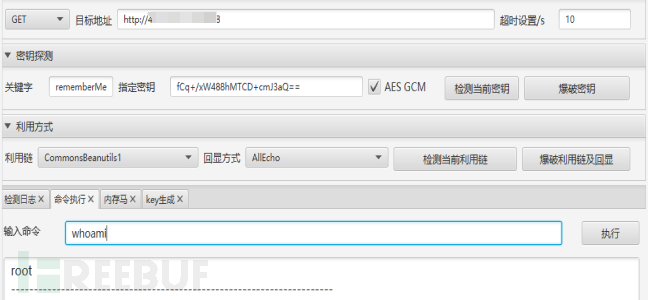
渗透测试-若依框架的杀猪交易所系统管理后台
前言 这次是带着摸鱼的情况下简单的写一篇文章,由于我喜欢探究黑灰产业,所以偶尔机遇下找到了一个加密H币的交易所S猪盘,我记得印象是上年的时候就打过这一个同样的站,然后我是通过指纹查找其它的一些站,那个站已经关…...
【免费】中国电子学会2024年03月份青少年软件编程Python等级考试试卷一级真题(含答案)
2024-03 Python一级真题 分数:100 题数:37 测试时长:60min 一、单选题(共25题,共50分) 1. 下列哪个命令,可以将2024转换成2024 呢?( A)(2分) A.str(2024) B.int(2024) C.fl…...
深入了解RTMP推流技术:视频汇聚EasyCVR低延迟与高稳定性分析
RTMP(Real Time Messaging Protocol)视频推流技术,作为音视频传输领域的关键技术之一,已经在直播、视频会议、在线教育等多个场景中得到了广泛应用。RTMP以其独特的优势,为实时音视频传输提供了高效、稳定的解决方案。…...
containerd手动配置容器网络
containerd手动配置容器网络 机器详情nerdctl启动一个不带网络的容器获取容器ID、PID与network namespace路径准备bridge插件的执行配置文件通过下面的命令调用bridge插件准备tuning插件文件执行下面的命令调用tuning插件准备portmap插件文件执行下面的命令调用portmap插件删除…...

数据迁移到 Django 模型表:详尽指南
数据迁移是许多应用程序开发过程中必不可少的一部分。在这篇文章中,我们将详细分析和总结如何通过一个定制的 Django 管理命令,将数据从 MySQL 数据库迁移到 Django 模型表中。这种方法可以确保数据在多个数据库之间有效且安全地迁移,同时避免…...

代码随想三刷二叉树篇4
代码随想三刷二叉树篇4 617. 合并二叉树题目代码 700. 二叉搜索树中的搜索题目代码 98. 验证二叉搜索树题目代码 530. 二叉搜索树的最小绝对差题目代码 501. 二叉搜索树中的众数题目代码 236. 二叉树的最近公共祖先题目代码 617. 合并二叉树 题目 链接 代码 /*** Definitio…...

『大模型笔记』如何让小型语言模型发挥作用!
如何让小型语言模型发挥作用! 文章目录 一. 如何让小型语言模型发挥作用!不可能的可能性小模型的潜力创新方法与突破实践与验证过滤系统与数据质量小模型的逐步改进信息理论蒸馏方法(新工作InfoSum)总结与展望Infini-Gram与N-gram模型的新时代后缀数组与高速计算二. 参考文献…...

jnp.diag
jnp.diag 是 JAX 库中用于创建对角矩阵或提取对角线元素的函数。具体功能取决于输入的形状: 当输入是一维数组时,jnp.diag 创建一个以该数组为对角线元素的对角矩阵。当输入是二维数组时,jnp.diag 提取并返回对角线元素。 函数签名 jnp.di…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
)
Vue3学习(接口,泛型,自定义类型,v-for,props)
一,前言 继续学习 二,TS接口泛型自定义类型 1.接口 TypeScript 接口(Interface)是一种定义对象形状的强大工具,它可以描述对象必须包含的属性、方法和它们的类型。接口不会被编译成 JavaScript 代码,仅…...

【Go语言基础【6】】字符串格式化说明
文章目录 零、格式化常用场景一、Go 字符串格式化核心概念二、常用格式化占位符1. 整数类型2. 浮点数类型3. 字符串与布尔类型4. 指针与通用类型 三、宽度与精度控制1. 宽度控制2. 精度控制(浮点数/字符串) 零、格式化常用场景 数值转字符串:…...
