191.回溯算法:组合总和|||(力扣)

代码解决
class Solution { public:vector<vector<int>> result; // 存储所有符合条件的组合vector<int> res; // 当前组合// 回溯函数void backtracing(int k, int n, int index, int sum) {// 如果当前组合的长度等于k,且总和等于nif (res.size() == k && sum == n) {result.push_back(res);return;}// 如果当前组合的长度超过k,或总和超过n,剪枝返回if (res.size() > k || sum > n) {return;}// 从index开始遍历1到9的数字for (int i = index; i <= 9; ++i) {res.push_back(i); // 将当前数字加入组合backtracing(k, n, i + 1, sum + i); // 递归调用回溯函数res.pop_back(); // 回溯,移除最后一个加入的数字}}// 主函数vector<vector<int>> combinationSum3(int k, int n) {backtracing(k, n, 1, 0); // 从1开始回溯return result; // 返回所有符合条件的组合} };类和成员变量
class Solution: 定义了一个解决方案类。vector<vector<int>> result: 用于存储所有满足条件的组合结果。每个组合都是一个整数数组。vector<int> res: 用于存储当前的组合。随着回溯的进行,这个向量会不断变化。方法:
backtracing
参数:
int k: 组合中数字的个数。int n: 目标和。int index: 当前选择数字的起始位置,防止重复选择。int sum: 当前组合的数字和。逻辑:
- 结束条件:
if (res.size() == k && sum == n): 当当前组合的长度等于k且总和等于n时,将当前组合添加到结果集中。if (res.size() > k || sum > n): 当当前组合的长度超过k或总和超过n时,直接返回,不再进行后续计算,这是剪枝操作,减少不必要的计算。- 循环遍历:
for (int i = index; i <= 9; ++i): 遍历从index到9的数字。index确保了每次递归时不重复选择已经选择过的数字。res.push_back(i): 将当前数字i添加到当前组合res中。backtracing(k, n, i + 1, sum + i): 递归调用回溯函数,i + 1确保下一个数字从当前数字的下一个开始,sum + i更新当前组合的和。res.pop_back(): 回溯时,将最后一个加入的数字移除,以便进行下一次组合。方法:
combinationSum3
- 逻辑:
- 调用
backtracing(k, n, 1, 0)从数字1开始查找组合。return result: 返回存储结果的result。回溯算法解释
回溯算法是一种系统地搜索问题解的算法,适用于满足特定条件的所有解。在这个问题中,回溯用于从数字1到9中选出k个数,使它们的和为n。每次递归调用都会在当前组合中添加一个新的数字,并继续尝试加入更多数字,直到满足条件或不满足条件而进行剪枝。通过回溯和剪枝,可以有效地找到所有满足条件的组合。
剪枝
class Solution { private:vector<vector<int>> result; // 存放结果集vector<int> path; // 符合条件的结果void backtracking(int targetSum, int k, int sum, int startIndex) {if (sum > targetSum) { // 剪枝操作return; }if (path.size() == k) {if (sum == targetSum) result.push_back(path);return; // 如果path.size() == k 但sum != targetSum 直接返回}for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝sum += i; // 处理path.push_back(i); // 处理backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯path.pop_back(); // 回溯}}public:vector<vector<int>> combinationSum3(int k, int n) {result.clear(); // 可以不加path.clear(); // 可以不加backtracking(n, k, 0, 1);return result;} };
相关文章:

191.回溯算法:组合总和|||(力扣)
代码解决 class Solution { public:vector<vector<int>> result; // 存储所有符合条件的组合vector<int> res; // 当前组合// 回溯函数void backtracing(int k, int n, int index, int sum) {// 如果当前组合的长度等于k,且总和等于nif (res.si…...

JupyterLab使用指南(二):JupyterLab基础
第2章 JupyterLab基础 2.1 JupyterLab界面介绍 JupyterLab的用户界面非常直观和灵活。它包括文件浏览器、工作区、多标签页、命令面板和侧边栏等功能。以下是各个部分的详细介绍: 2.1.1 文件浏览器 文件浏览器位于界面左侧,用于导航和管理文件。你可…...

ubuntu18.04 + openssl + engine + pkcs11+ softhsm2 双向认证测试
安装环境 openssl 1.1.1 pkcs11-tool (由sudo apt-get install opensc 安装) libpksc11 (需源码安装apt install 只有libp11, 源码安装才有 libpksc11.so -> pkcs11.so) softhsm2 (由sudo apt-get install softhsm…...
【C++】类和对象2.0
俺来写笔记了,哈哈哈,浅浅介绍类和对象的知识点! 1.类的6个默认成员函数 俺们定义一个空类: class N {}; 似乎这个类N里面什么都没有,其实不是这样子的。这个空类有6个默认的成员函数 。 默认成员函数:…...
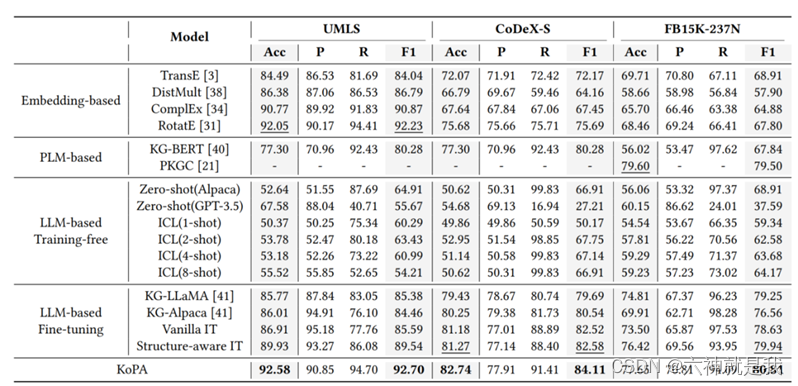
【LLM之KG】KoPA论文阅读笔记
研究背景 知识图谱补全(KGC)是通过预测知识图谱中缺失的三元组来完善知识图谱的信息。传统方法主要基于嵌入和预训练语言模型,但这些方法往往忽视了知识图谱的结构信息,导致预测效果不佳。 研究目标 本文的研究目标是探索如何将…...

UI设计速成课:理解模态窗口与非模态窗口的区别
我们日常所说的弹性框架是非常笼统的概念。我们习惯性地称之为对话框架、浮动层和提示条。弹性框架可以分为两种:模态弹性框架和非模态弹性框架。产品需要弹性框架来传递信息,用户需要弹性框架来接受反馈,但是没有经过推敲的弹出窗口设计很容易让用户感到…...
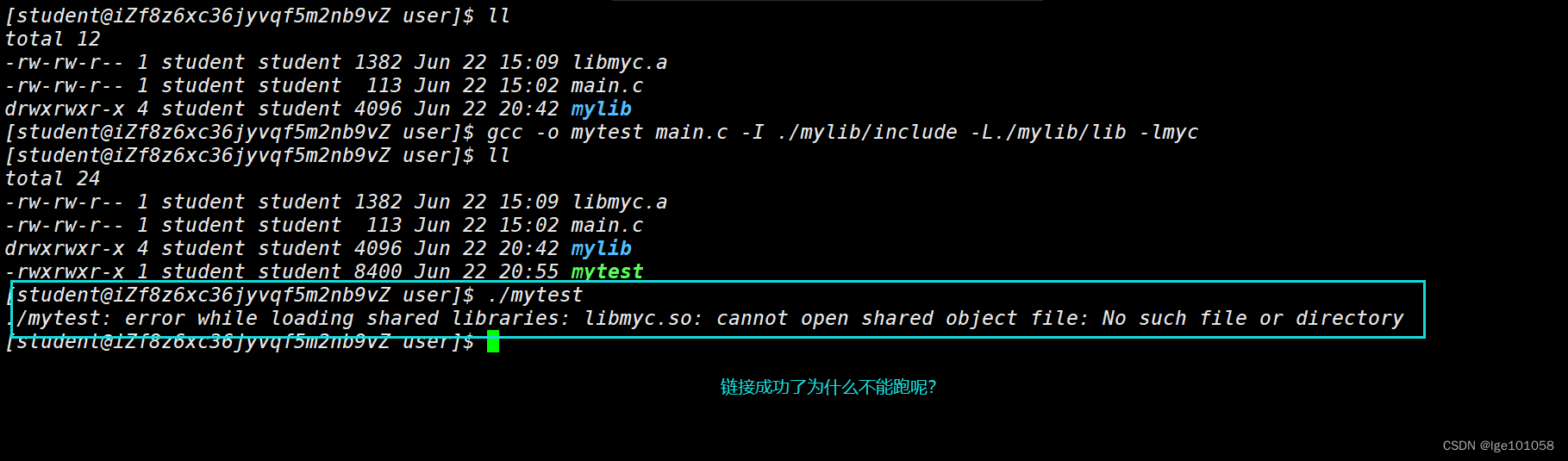
【Linux】基础IO_4
文章目录 六、基础I/O4. 动静态库 未完待续 六、基础I/O 4. 动静态库 既然我们能够成功创建静态库了,接下来我们将这个代码打包成动态库: shared: 表示生成共享库格式 fPIC:产生位置无关码(position independent code) 动态库库名规则&…...

C++模板类原理讲解
C模板类原理讲解 C模板是一种强大的编译期工具,它允许我们创建通用的、类型无关的类和函数。模板的主要目的是实现代码的重用和泛型编程。模板类的原理涉及以下几个方面: 模板的定义和实例化模板的类型参数模板特化模板的编译过程模板的优点和缺点 1.…...
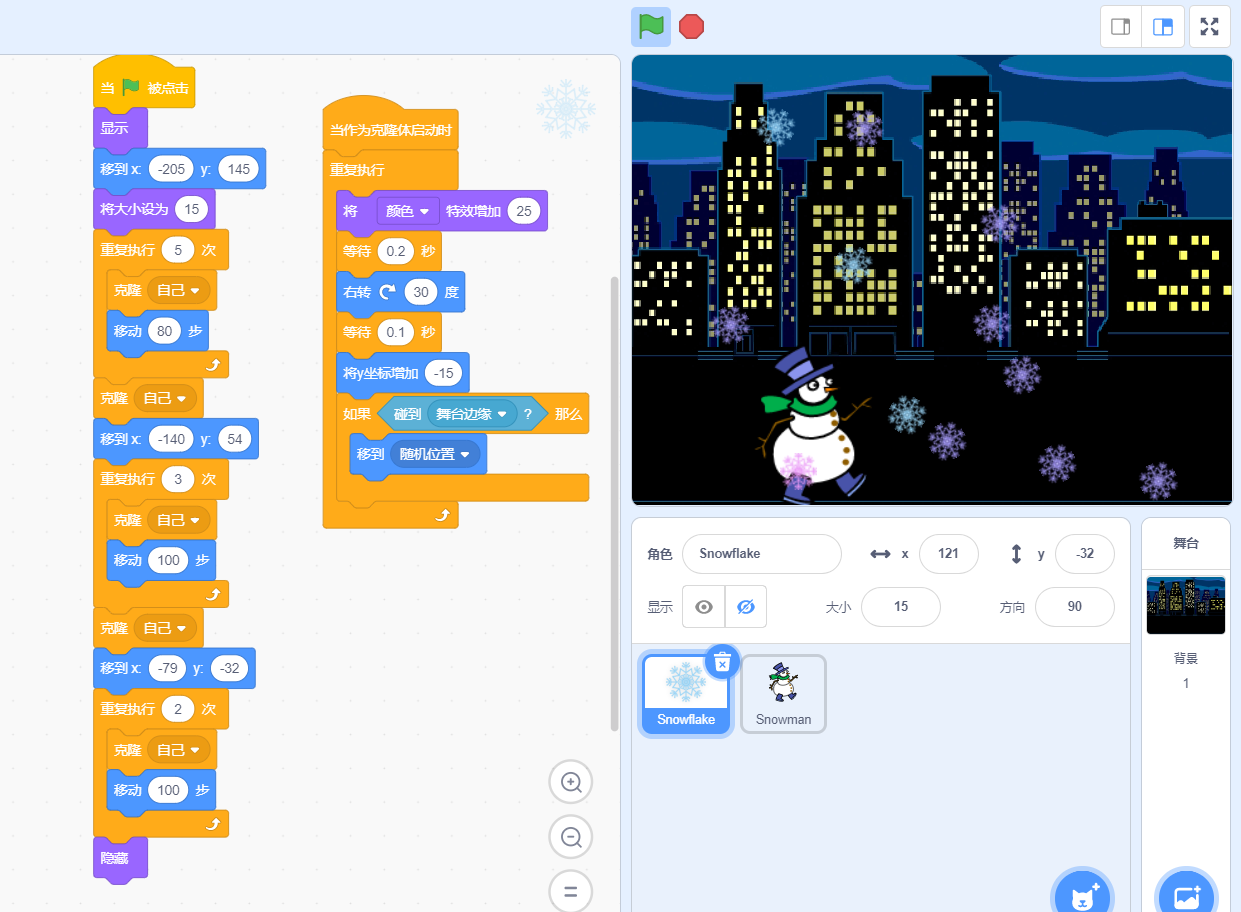
scratch编程03-反弹球
这篇文章和上一篇文章《scratch3编程02-使用克隆来编写小游戏》类似(已经完全掌握了克隆的可以忽略这篇文章),两篇文章都使用到了克隆来编写一个小游戏,这篇文章与上篇文章不同的是,本体在进行克隆操作时,不…...

postgresql数据库进阶知识
postgresql数据库进阶知识 # 如果表存在就先删除 drop table if exists student; # 创建学生表 # id serial not null 表示id自增 # id integer not null 表示id不自增 create table student (id serial not nullconstraint student_pkprimary…...
关于HTTP劫持,该如何理解、防范和应对
一、引言 HTTP劫持(HTTP Hijacking)是一种网络安全威胁,它发生在HTTP通信过程中,攻击者试图通过拦截、篡改或监控用户与服务器之间的数据流量,以达到窃取敏感信息或执行恶意操作的目的。今天我们就来详细了解HTTP劫持…...
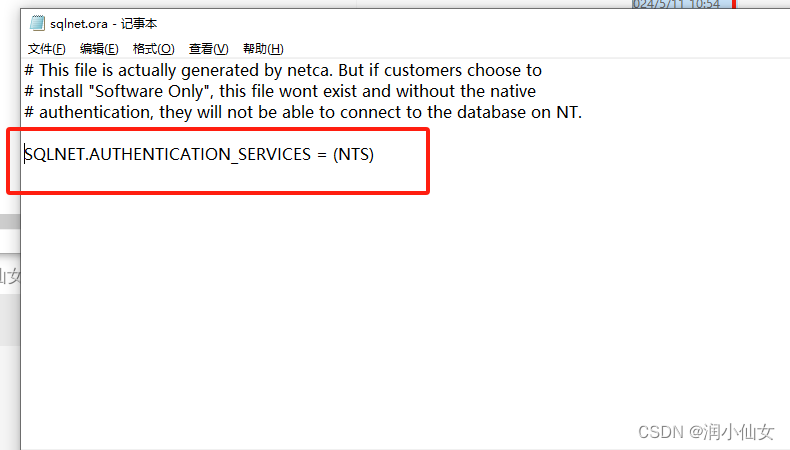
System.Data.OracleClient.OracleException:“ORA-12571: TNS: 包写入程序失败
System.Data.OracleClient.OracleException:“ORA-12571: TNS: 包写入程序失败 解决方法: 首先%oracle_home%/network/admin下的sqlnet.ora文件,把SQLNET.AUTHENTICATION_SERVICES (NTS)加个 # 注释掉就好了...
saas产品运营案例 | 联盟营销计划如何帮助企业提高销售额?
在当今数字化时代,SaaS(软件即服务)产品已成为企业提高效率、降低成本的重要工具。然而,面对激烈的市场竞争,如何有效地推广SaaS产品、提高销售额,成为许多企业面临的挑战。林叔将以ClickFunnels为例&#…...
模式分解算法-满足3NF的无损且保持函数依赖的分解算法、满足BCNF的无损连接分解算法
一、引言 1、对指定的关系模式,若范式级别较低,为第一范式或第二范式,由于存在数据冗余或更新异常问题,在实际中一般是不可用的,关系模式的规范化就是将满足低一级的关系模式分解为若干满足高一级范式的关系模式的集合…...
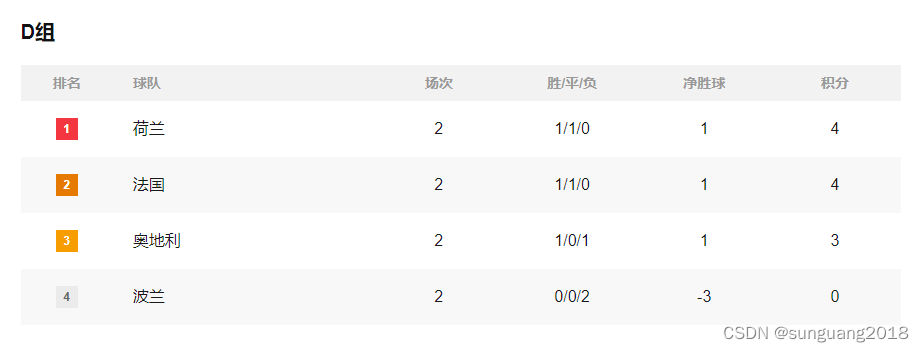
荷兰与法国战平,双方能携手出现?
就在昨天晚上,荷兰队经历了90分钟的鏖战,最终0-0与法国队握手言和。此役,哈维-西蒙斯为荷兰队打进一球,但进球被判无效。从目前的积分形势来看,双方基本上确定携手晋级16强赛。本场比赛,荷兰队后卫内森-阿克…...

数据可视化实验二:回归分析、判别分析与聚类分析
目录 一、使用回归分析方法分析某病毒是否与温度呈线性关系 1.1 代码实现 1.2 线性回归结果 1.3 相关系数验证 二、使用判别分析方法预测某病毒在一定的温度下是否可以存活,分别使用三种判别方法,包括Fish判别、贝叶斯判别、LDA 2.1 数据集展示&am…...

FL论文专栏|设备异构、异步联邦
论文:Asynchronous Federated Optimization(12th Annual Workshop on Optimization for Machine Learning) 链接 实现Server的异步更新。每次Server广播全局Model的时候附带一个时间戳,Client跑完之后上传将时间戳和Model同时带回…...
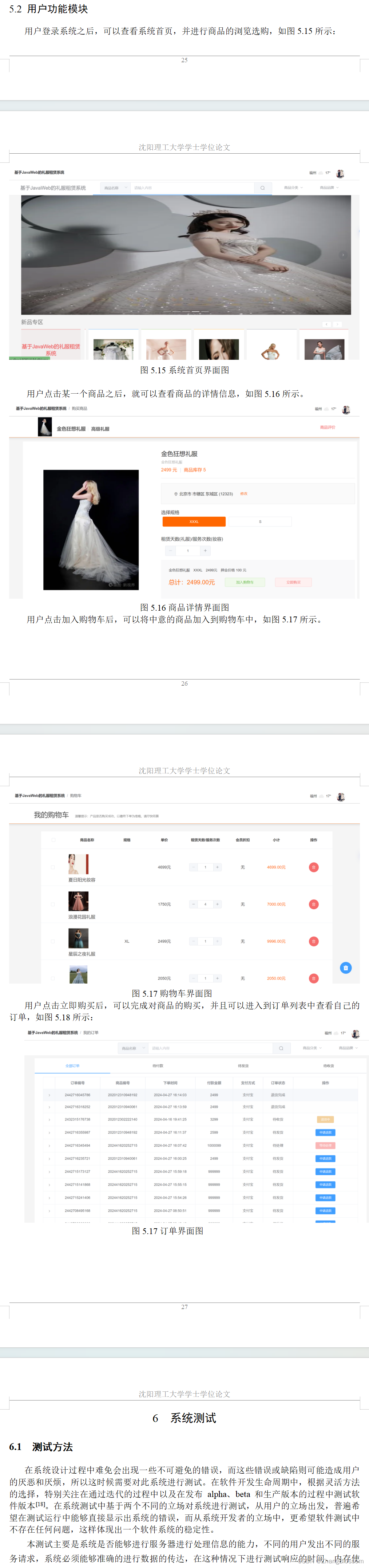
【Java毕业设计】基于JavaWeb的礼服租赁系统
文章目录 摘 要Abstract目录1 绪论1.1 课题背景和意义1.2 国内外研究现状1.2.1 国外研究现状 1.3 课题主要内容 2 开发相关技术介绍2.1 Spring Boot框架2.2 Vue框架2.3 MySQL数据库2.4 Redis数据库 3 系统分析3.1 需求分析3.1.1 用户需求分析3.1.2 功能需求分析 3.2 可行性分析…...

代码随想录训练营Day 66|卡码网101.孤岛的总面积、102.沉没孤岛、103.水流问题、104.建造最大岛屿
1.孤岛的总面积 101. 孤岛的总面积 | 代码随想录 代码:(bfs广搜) #include <iostream> #include <vector> #include <queue> using namespace std; int dir[4][2] {1,0,0,1,-1,0,0,-1}; int count; void bfs(vector<vector<int>>&a…...

根据状态转移写状态机-二段式
目录 描述 输入描述: 输出描述: 描述 题目描述: 如图所示为两种状态机中的一种,请根据状态转移图写出代码,状态转移线上的0/0等表示的意思是过程中data/flag的值。 要求: 1、 必须使用对应类型的状…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
