使用vue3,vite,less,flask,python从零开始学习硅谷外卖(16-40集)
严正声明!
重要的事情说一遍,本文章仅供分享,文章和代码都是开源的,严禁以此牟利,严禁侵犯尚硅谷原作视频的任何权益,我知道学习编程的人各种各样的心思都有,但这不是你对开源社区侵权的理由!
第16集:这一集老师啰嗦了一集,核心就两句话,一个是对axios的二次封装,还有一个是对promise结果再次封装使得其可以直接获取data,老师的代码应该是可以用的。这个写法只有get和post,不过不重要了,以后有需要在重新写,程序员就是要懒一点。
第17集:这集的封装其实也没什么必要。。。就是为了调用接口时方便一点特地把它弄成一个变量。。。不过这里还是学到东西了,param参数就是在路径里的,query参数在?后面的。这里可以看到,query参数和写在body请求体里的进行ajax请求的方式是一样的。但是不能混用这两者。
第18集:这一集就是上传代码到github,只不过这件事分三步,创建本地仓库,关联远程仓库,不过先将源码设为master,之后的每次改动都会被设置为分支,这样就可以返回任何时候的状态。Git init 在本地初始化git仓库,git add *将本地所有文件(除了.gitignore中指定的)纳入仓库中,git commit -m "init gshop"将仓库提交并命名为init gshop。
第20集:这一章其实就是简单的跨域,但是视频不完整中间跳过了一段,没关系我们直接用vite来写,当然我们可以在后端设置响应头,但我们是前端,就用vite的代理服务器来搞。
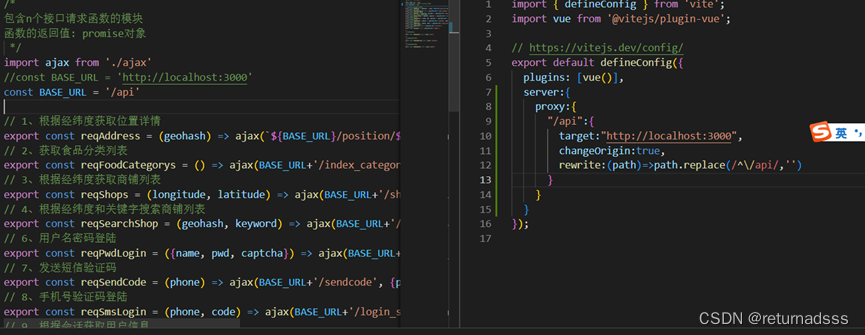
我们yarn dev后默认端口5174,跨域原理就是我们在浏览器端请求/api而不是http://localhost:3000,浏览器会自动拼接为http://localhost:5174/api,这是通过vite配置,在本地开启的服务器端请求http://localhost:3000, 在api后面还可以加路径,再将请求返回来,就相当于让本机的服务器中转了一下。
第21集:引入状态管理,跟之前引入vue-router差不多,稍加修改即可,这里分成state,mutations,actions,getters只是为了当内容多的时候方便管理,可以直接写在index.js里面都没问题。
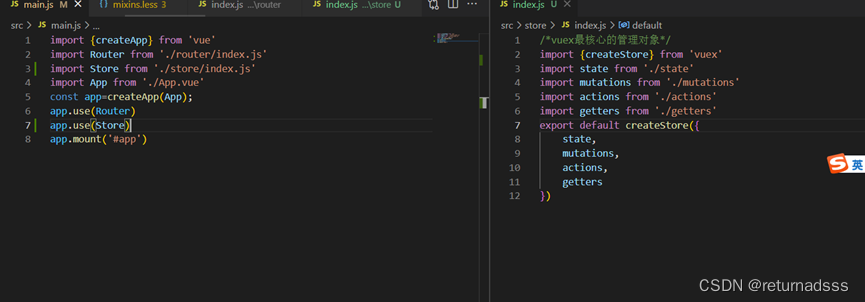
第22集:这一集就是照例抄代码,有些高度封装(老师喜欢的写法)多看几遍,有些是解构赋值,有些是对象属性值简写。
第23集:这一集基本没什么问题,出现问题可以按代码逻辑推一下,我的问题是后台的接口写错了,获取不到数据,改一下就好了。
第24集,25集:照着写没大问题。
第26集:这一集有点坑,首先是这个图片接口已经废弃了,我直接用网上的接口来代替,按照这个接口数据,只考虑shops.json的数据的话,这个根据经纬度其实只能返回一个商家,算了我们直接改接口,返回所有商家。
第27-第31集:没啥难点,照着敲就行了.
第32,33集:简单的防抖节流,没啥好说的,${}外面不加括号也可以。
第34,35集:也是照着写就行了,有一个知识点就是自定义事件的冒泡传递。还有一个是前台只能做合法性验证,没法安全验证。第35集复习,一般在mounted异步获取数据。打开network看ajax请求的情况,这个可以看尚硅谷的ajax或者promise课程。
第36集:这一集跟老师比起来我的后台没有返回动态验证码,搜点资料改一下。把接口写好更新。
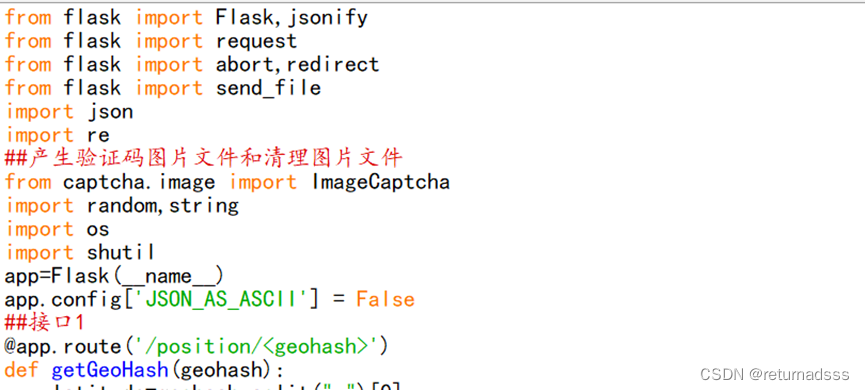

这样就可以返回图形验证码了,这里的思路是每次在image文件夹下产生一个验证码图片并返回它,然后下一次访问该路径时清空image文件夹下图片,然后再产生返回。想更完备一点连image文件夹都可以在代码里创建,不过python不是前端的重点,这里不赘述了。
第37集就改名字。
第38集:好家伙,短信验证码接口又搞起来了,抱着一丝希望node一下这个sms_util.js,果然报错。送佛送到西,我把python的短信后台接口也写一遍吧。
后面两集笔记忘了保存,问题不大,可以评论区问我,我给你发调通了的源码。
相关文章:

使用vue3,vite,less,flask,python从零开始学习硅谷外卖(16-40集)
严正声明! 重要的事情说一遍,本文章仅供分享,文章和代码都是开源的,严禁以此牟利,严禁侵犯尚硅谷原作视频的任何权益,我知道学习编程的人各种各样的心思都有,但这不是你对开源社区侵权的理由&am…...

坚持就是胜利
很多朋友,可能坚持了多年的同等学力申硕考试,依然没有通过。如果你感到困惑,感到迷茫,要坚信:坚持就能胜利。有很多人跟你一样,一直坚持在路上,没有停止脚步。 生活没有你想象的那么好ÿ…...
 或者转置 intrinsic (内参)矩阵的原因)
代码中出现转置 pose (c2w,外参矩阵) 或者转置 intrinsic (内参)矩阵的原因
在代码中见到 pose(c2w),intrinsic 矩阵的转置,觉得比较奇怪。 后来想了一下为什么。下面解释一下: 用 c2w 矩阵举例子。理论上,一个 c2w 左乘上 一个相机坐标系下的点 P的坐标,能够得到该点在…...

2023 年腾讯云服务器配置价格表出炉(2核2G/2核4G/4核8G/8核16G、16核32G)
腾讯云轻量应用服务器为轻量级的云服务器,使用门槛低,按套餐形式购买,轻量应用服务器套餐自带的公网带宽较大,4M、6M、7M、10M、14M及20M套餐可选,如果是云服务器CVM这个带宽价格就要贵很多了。 1、轻量应用服务器优惠…...
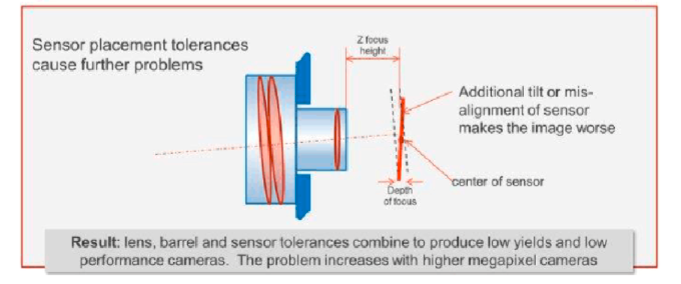
相机出图画面一半清晰,一半模糊的原因是什么?
1、问题背景:在做项目的过程中,有遇到过几次,出图后画面是一半清晰,一半模糊的现象,再重新对焦也是一样。但换了个镜头后就好了,这应该是镜头的质量问题,但导致镜头出现这种问题的具体原因是什么…...
Rust学习入门--【4】Rust 输出到命令行
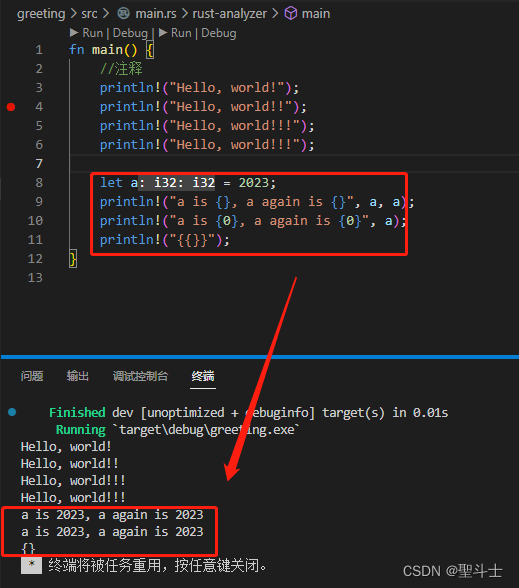
Rust 语言中的打印“函数” 学习新的编程语言时,大家都喜欢打印“Hello World”。 在Rust中怎样将字符串打印出来呢? Rust 输出文字的方式主要有两种:println!() 和 print!()。 “函数”差异说明: 这两个"函数"都是向…...

Vector刷写方案—vFlash工具介绍
我是穿拖鞋的汉子,魔都中坚持长期主义的工科男! 今天魔都天气是连阴雨,滴滴答答的下个不停,心情也跟着潮湿起来!老规矩分享一段喜欢的文字,避免成为高知识低文化的工程师: 即使在真正的困境里,也一直提示自己,每次自恋不得超过十分钟! 那些看似无法度过得困境,不是…...
》)
【阶段总结】《非结构化信息分析应用与实践(筹)》
《非结构化信息分析应用与实践(筹)》Part 1.知识储备一、机器学习 1.几种常见的有监督学习算法 2.几种常见的无监督学习算法 3.数据挖掘基础知识 30 问 二、神经网络与深度学习 1.MP神经网络模型(附实例代码讲解) 2.图解LST…...
七大设计原则之迪米特法则应用
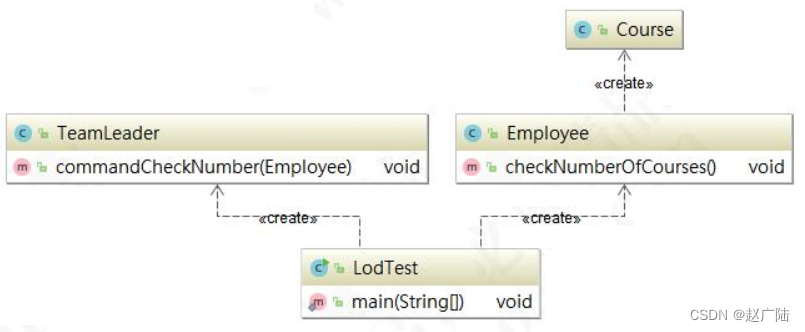
目录1 迪米特法则介绍2 迪米特法则应用1 迪米特法则介绍 迪米特原则(Law of Demeter LoD)是指一个对象应该对其他对象保持最少的了解,又叫最少知 道原则(Least Knowledge Principle,LKP),尽量降低类与类之…...

curl命令用法精简整理
目录1.GET请求1.1 形式1:1.2 形式2:2.POST请求2.1 无入参:2.2 form传参(文件):2.3 json入参:2.4 json文件入参:3.请求计时3.1 time命令(Linux):3.…...

Fluent Python 笔记 第 5 章 一等函数
在 Python 中,函数是一等对象。编程语言理论家把“一等对象”定义为满足下述条件的程 序实体: 在运行时创建能赋值给变量或数据结构中的元素 • 能作为参数传给函数能作为函数的返回结果 5.1 把函数视作对象 会用 map。 5.2 高阶函数 接受函数为参数࿰…...

卡尔曼滤波器与DSP实现
卡尔曼滤波器是利用系统状态方程,结合测量结果对系统状态进行进行最优估计的算法。本文介绍它的主要公式,并举例在C6000 DSP上实现。 推荐资料 KalmanFilter.NETUnderstanding Kalman Filters卡尔曼滤波与组合导航原理 “If you can’t explain it sim…...

引入QQ邮箱发送验证码进行安全校验
最近想给自己的项目在注册时加点安全校验,本想着使用短信验证码,奈何囊中羞涩只能退而求次改用QQ邮箱验证注册~ 一.需求分析 场景:用户输入自己的邮箱,点击获取验证码,后台会发送一封邮件到对应邮箱中。 分析&#x…...

【c++】数组
文章目录一维数组定义方式数组名案例案例1:元素逆置案例2:冒泡排序二维数组定义方式数组名案例:考试成绩统计数组特点: 1、每个数据元素放在一块连续的内存空间中; 2、数组中每个数据元素都是相同数据类型;…...
线程池的简单实现:Java线程池初学者必读指南
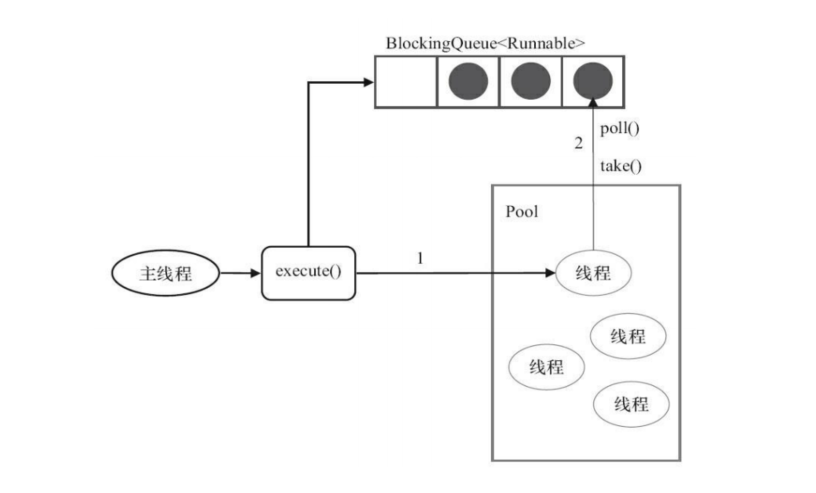
"作为一名Java开发者,是否曾经遇到过多线程并发的问题?线程数量过多时,会导致资源浪费,应用性能下降,甚至发生线程死锁的情况。那么,有没有一种方法可以有效地管理线程,避免这些问题呢&…...

【C#】[带格式的字符串] 复合格式设置字符串与使用 $ 的字符串内插 | 如何格式化输出字符串
复合格式输出 string name "Fred"; String.Format("Name {0}, hours {1:hh}", name, DateTime.Now);通过指定相同的参数说明符,多个格式项可以引用对象列表中的同一个元素。 例如,通过指定“0x{0:X} {0:E} {0:N}”等复合格式字符…...

Lecture4 反向传播(Back Propagation)
目录 1 问题背景 1.1计算图(Computational Graph) 1.2 激活函数(Activation Function)引入 1.3 问题引入 2 反向传播(Back Propagation) 2.1 为什么要使用反向传播 2.2 前馈运算(Forward Propagation…...
Power BI 筛选器函数---Window实例详解
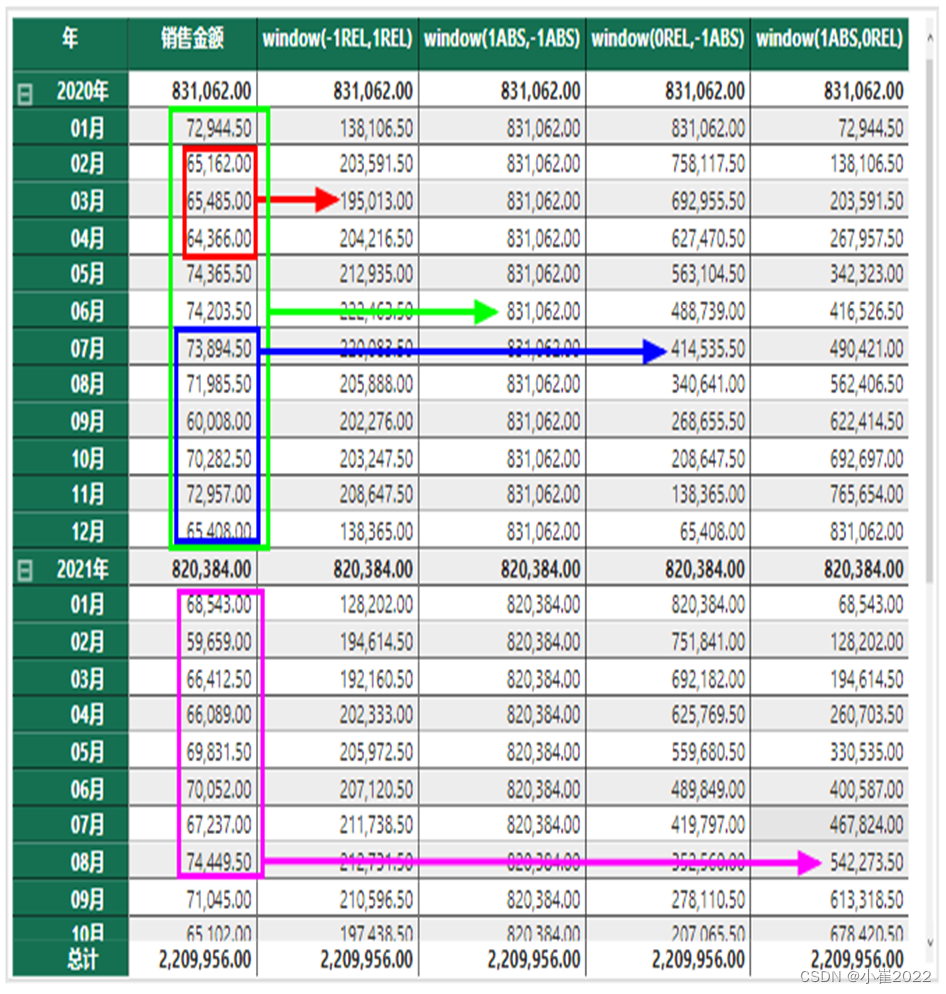
一、Window函数 语法: Window ( <起始位置>,<起始位置类型>,<结束位置>,<结束位置类型>, [<关系>], [<OrderBy>],[空白],[PartitionBy] ) 含义: 对指定分区(PartitioinBy)中的行(关系表&…...

基础篇—如何创建css样式表,并集成到html文件中?
CSS 创建 HTML相当于一个页面的结构,CSS相当于页面的装饰,浏览器当读到一个样式表时,浏览器会根据它来格式化 HTML 文档。 如何插入样式表 插入样式表的方法有三种: 外部样式表(External style sheet)内部样式表(Internal style sheet)内联样式(Inline style)1、外…...

WindowsServer服务器系列:部署FTP文件服务
1、点击“开始”菜单,选择“服务器管理器” 2、在接下来弹出页面中选择“添加角色和功能” 3、接下来点击“下一步” 4、接下来选择“基于角色或基于功能的安装”并点击“下一步” 5、选择“从服务器池中选择服务器”并点击“下一步” 6、接下来选中“Web 服务器(II…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...
