LeetCode 算法:二叉树的直径 c++
原题链接🔗:二叉树的直径
难度:简单⭐️
题目
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
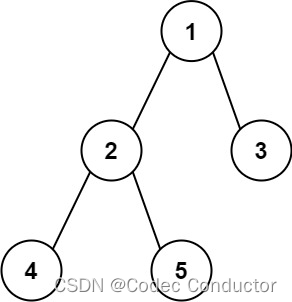
输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2]
输出:1
提示:
- 树中节点数目在范围 [1, 104] 内
- -100 <= Node.val <= 100
二叉树直径
二叉树的直径通常指的是二叉树中任意两个节点间的最长路径的长度。这个路径不一定经过根节点。二叉树的直径可以通过以下步骤求解:
计算高度:首先,需要计算二叉树的高度。这可以通过递归函数实现,递归地计算左子树和右子树的高度,并返回两者中较大的一个加上当前节点的高度。
更新直径:在计算高度的同时,可以更新直径。对于每个节点,其左子树的高度加上其右子树的高度就是通过该节点的路径长度,这个长度可能是当前的直径。
返回结果:最终,返回记录的最大直径值。
题解
递归法
- 解题思路:
理解问题:首先,明确题目要求的“直径”是指二叉树中任意两个节点之间的最长路径长度。这个路径可以不经过根节点。
递归计算高度:二叉树的高度可以通过递归计算得到。对于每个节点,其高度是其左子树和右子树高度的最大值加1。
同时更新直径:在计算高度的过程中,可以同时更新直径。对于每个节点,其左子树的高度加上其右子树的高度,就是通过该节点的一条可能的最长路径长度。这个长度可能是当前的直径。
使用辅助变量:由于直径的计算依赖于递归过程中的信息,因此可以使用一个辅助变量来存储遍历过程中发现的最长路径长度。
遍历结束:当递归遍历完整棵树后,辅助变量中存储的就是二叉树的直径。
注意边界条件:在递归函数中,如果当前节点为空,应该返回0,因为空树的高度是0。
返回结果:最终,返回辅助变量中的值作为二叉树的直径。
- 复杂度:
- 时间复杂度:O(N),其中 N 为二叉树的节点数,即遍历一棵二叉树的时间复杂度,每个结点只被访问一次。
- 空间复杂度:O(Height),其中 Height 为二叉树的高度。由于递归函数在递归过程中需要为每一层递归函数分配栈空间,所以这里需要额外的空间且该空间取决于递归的深度,而递归的深度显然为二叉树的高度,并且每次递归调用的函数里又只用了常数个变量,所以所需空间复杂度为 O(Height)。
- c++ demo:
#include <iostream>
#include <algorithm>
#include <climits>
#include <queue>// 定义二叉树的节点结构
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 解决方案类
class Solution {
public:// 计算二叉树的直径int diameterOfBinaryTree(TreeNode* root) {this->maxDiameter = 0; // 初始化最大直径为0calculateHeight(root); // 计算树的高度并更新最大直径return maxDiameter;}private:int maxDiameter; // 用于存储最大直径// 计算以node为根的二叉树的高度,并更新最大直径int calculateHeight(TreeNode* node) {if (!node) return 0; // 如果节点为空,返回高度0// 计算左子树和右子树的高度int leftHeight = calculateHeight(node->left);int rightHeight = calculateHeight(node->right);// 更新最大直径,如果通过当前节点的路径更长maxDiameter = std::max(maxDiameter, leftHeight + rightHeight);// 返回当前节点的高度,即左右子树高度的最大值加1return std::max(leftHeight, rightHeight) + 1;}
};// 主函数,用于测试算法
int main() {// 创建一个示例二叉树// 1// / \// 2 3// / \// 4 5TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);// 创建解决方案实例Solution solution;// 计算并输出二叉树的直径std::cout << "The diameter of the binary tree is: " << solution.diameterOfBinaryTree(root) << std::endl;// 清理分配的内存(在实际应用中应该使用智能指针来避免内存泄漏)delete root->left->left;delete root->left->right;delete root->left;delete root->right;delete root;return 0;
}
- 输出结果:
The diameter of the binary tree is: 3
相关文章:

LeetCode 算法:二叉树的直径 c++
原题链接🔗:二叉树的直径 难度:简单⭐️ 题目 给你一棵二叉树的根节点,返回该树的 直径 。 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。 两节点之间路径的 长度 由…...
盘立方期货Kdj幅图指标公式源码
盘立方期货Kdj幅图指标公式源码: N:250; WR1:100-100*(HHV(HIGH,N)-CLOSE)/(HHV(HIGH,N)-LLV(LOW,N)),DOT,COLORLIGHTGREEN; EW:EMA(WR1,5); STICKLINE(WR1<20,WR1,20,1,0),COLORYELLOW; STICKLINE(WR1>80,WR1,80,1,0),COLORYELLOW; RSV:(CLOSE-LLV(LOW…...
SkyWalking 极简入门
1. 概述 1.1 概念 SkyWalking 是什么? FROM Apache SkyWalking 分布式系统的应用程序性能监视工具,专为微服务、云原生架构和基于容器(Docker、K8s、Mesos)架构而设计。 提供分布式追踪、服务网格遥测分析、度量聚合和可视化一体…...
)
本篇内容:ArkTS开发系列之事件(2.8.1触屏、键鼠、焦点事件)
上篇回顾: ArkTS开发系列之导航 (2.7动画) 本篇内容:ArkTS开发系列之事件(2.8.1触屏、键鼠、焦点事件) 一、知识储备 1. 触屏事件:包括点击事件、拖拽事件、触摸事件。 点击事件 Button()....onClick(…...
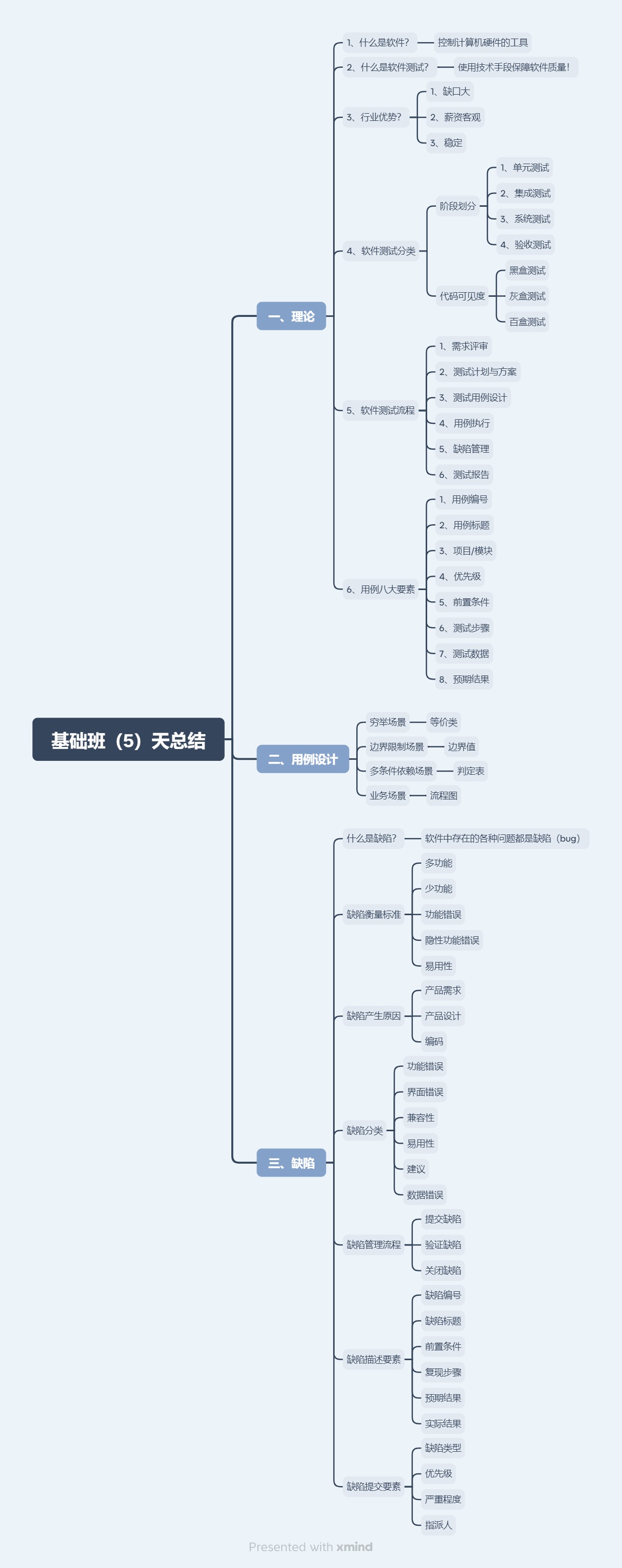
测试的基础知识大全【测试概念、分类、模型、流程、测试用例书写、用例设计、Bug、基础功能测试实战】
测试基础笔记 Day01阶段⽬标⼀、测试介绍⼆、测试常⽤分类2.1 阶段划分单元测试集成测试系统测试验收测试 2.2 代码可⻅度划分⿊盒测试:主要针对功能(阶段划分->系统测试)灰盒测试:针对接⼝测试(阶段划分->集成测…...
Power Apps
目录 一、引言1、Power Apps2、应用场景3、Power Apps的优势与前景4、补充 二、数据源介绍1、SharePoint2、Excel3、Dataverse4、SQL5、补充(1)OneDrive 三、Power Apps应用类型1、画布应用2、模型驱动应用3、网站 Power Pages 四、Power Automate五、Po…...

qt图像处理-将OpenCV的cv::Mat类型转换为QImage类型
在使用Qt进行图像处理时,经常需要将OpenCV的cv::Mat类型转换为QImage类型。以下是几种有效的方法,可以根据具体情况选择合适的方法进行转换。 方法一:直接使用QImage构造函数 这种方法直接使用QImage的构造函数,通过传递cv::Mat的指针和相关参数来创建QImage对象。这种方…...

代码随想录训练营第十八天 530二叉搜索树的最小绝对差 501二叉搜索树中的众数 236二叉树的最近公共祖先
第一题: 原题链接:530. 二叉搜索树的最小绝对差 - 力扣(LeetCode) 思路: 使用中序遍历的方式:左中右。 定义一个pre节点来存放当前节点的前一个节点。 在中序的时候处理递归逻辑: 首先先向…...

微信小程序之横向列表展示
效果图 参考微信小程序可看 代码: <view class"lbtClass"><view class"swiper-container"><scroll-view class"swiper" scroll-x"true" :scroll-left"scrollLeft"><block v-for"(six…...
无人机巡检小羊仿真
详细视频地址 仿真效果 可视化三维仿真 gazebo物理仿真 px4 飞控仿真 仿qgc简易地面站 详细视频地址...

springboot redission 分布式锁
Spring Boot中使用Redisson实现分布式锁的方法如下: 1. 首先,需要在项目中引入Redisson依赖。在pom.xml文件中添加以下依赖: xml <dependency> <groupId>org.redisson</groupId> <artifactId>redisson<…...

Vuex中的重要核心属性
Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 Vuex 的核心属性包括: State: State 是 Vuex 存储数据的地方,类似于组件中的 data。它…...

Redis哨兵集群搭建
一、安装Redis 1.安装依赖 yum install -y gcc tcl2.将Redis压缩包解压到对应的目录 tar -zxvf redis-2.8.0.tar.gz mv redis-2.8.0 /usr/local3.编译 cd /usr/local/redis-2.8.0 make && make install4.配置redis.conf # 任意ip都可以访问 bind 0.0.0.0 # 关闭保…...

网络爬虫requests库使用指南
目录 引言 安装requests库 基本用法 发送GET请求 发送POST请求 处理请求头和Cookies 设置请求头 使用Cookies 会话管理 异常处理 流式上传和下载 结语 引言 在Python中进行HTTP请求时,requests库是一个强大且易于使用的第三方库。它允许你发送各种HTTP请…...

VSCODE 配置C++ 与OPENCV
主要是两个json设置 c_cpp_properties.json {"configurations": [{"name": "Win32","includePath": ["${workspaceFolder}/**"],"defines": ["_DEBUG","UNICODE","_UNICODE"],&qu…...
C语言小例程28/100
题目:利用递归方法求5!。 程序分析:递归公式:fnfn_1*4! #include <stdio.h>int main() {int i;int fact(int);for(i0;i<6;i){printf("%d!%d\n",i,fact(i));} } int fact(int j) {int sum;if(j0){sum1;} else {sumj*fac…...
WPF文本绑定显示格式StringFormat设置-特殊格式时间日期和多数据绑定
WPF文本绑定显示格式StringFormat设置 特殊格式设置日期/时间使用系统默认样式自定义格式: 绑定多个属性(多重绑定)多重绑定中的特殊字符示例: 特殊格式设置 在Textblock等文本控件中,我们经常要显示一些日期和时间&a…...

Java包介绍
今天看jdk文档,顺便写一下java几个包的作用。 java.applet 主要用于创建java applet小应用程序,可以嵌入到网页中能够呈现出特殊的效果,现在基本已经被废弃,很少使用。 java.awt AWT 是Abstract Window ToolKit (抽象窗口工具包…...

【2024.6.21】今日科技时事:科技前沿大事件
人不走空 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌赋:斯是陋室,惟吾德馨 目录 🌈个人主页:人不走空 💖系列专栏:算法专题 ⏰诗词歌…...

LeetCode:经典题之1491、896 题解与延伸
系列目录 88.合并两个有序数组 52.螺旋数组 567.字符串的排列 643.子数组最大平均数 150.逆波兰表达式 61.旋转链表 160.相交链表 83.删除排序链表中的重复元素 389.找不同 1491.去掉最低工资和最高工资后的工资平均值 896.单调序列 206.反转链表 92.反转链表II 141.环形链表 …...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
