图的关键路径算法
关键路径算法(Critical Path Method, CPM)是一种用于项目管理和调度的技术,通过分析项目任务的最早开始时间、最晚完成时间和总时差,找出项目中关键的任务路径。这条关键路径决定了项目的最短完成时间,因为关键路径上的每个任务都不能被延迟,否则整个项目会被延迟。
关键路径算法的步骤
-
构建有向图:将项目中的任务和任务间的依赖关系表示为有向图,节点表示任务,边表示依赖关系。
-
计算任务的最早开始时间和最早完成时间:
- 最早开始时间(ES, Earliest Start Time):某任务可以开始的最早时间。
- 最早完成时间(EF, Earliest Finish Time):某任务可以完成的最早时间,EF = ES + 任务持续时间。
-
计算任务的最晚开始时间和最晚完成时间:
- 最晚完成时间(LF, Latest Finish Time):某任务必须完成的最晚时间,不会延误项目。
- 最晚开始时间(LS, Latest Start Time):某任务必须开始的最晚时间,LS = LF - 任务持续时间。
-
计算总时差和自由时差:
- 总时差(Total Float, TF):某任务可以延迟的时间,TF = LF - EF 或 TF = LS - ES。
- 自由时差(Free Float, FF):某任务可以延迟的时间,不会延误后续任务,FF = min(ES of next tasks) - EF of current task。
-
找出关键路径:关键路径上的任务总时差为 0,连接这些任务的路径就是关键路径。
示例与实现
考虑一个简单的项目,有 6 个任务(A、B、C、D、E、F),以及它们的持续时间和依赖关系如下:
- 任务 A:持续时间 3 天
- 任务 B:持续时间 2 天,依赖于任务 A
- 任务 C:持续时间 4 天,依赖于任务 A
- 任务 D:持续时间 2 天,依赖于任务 B
- 任务 E:持续时间 1 天,依赖于任务 C
- 任务 F:持续时间 3 天,依赖于任务 D 和任务 E
构建有向图
A (3)
| \
B (2) C (4)
| |
D (2) E (1)\ /\ /F (3)
计算最早开始时间和最早完成时间
- 任务 A: ES = 0, EF = 3
- 任务 B: ES = 3, EF = 5
- 任务 C: ES = 3, EF = 7
- 任务 D: ES = 5, EF = 7
- 任务 E: ES = 7, EF = 8
- 任务 F: ES = 8, EF = 11
计算最晚开始时间和最晚完成时间
- 任务 F: LF = 11, LS = 8
- 任务 D: LF = 8, LS = 6
- 任务 E: LF = 8, LS = 7
- 任务 B: LF = 6, LS = 4
- 任务 C: LF = 7, LS = 3
- 任务 A: LF = 3, LS = 0
计算总时差和自由时差
- 任务 A: TF = 0
- 任务 B: TF = 1
- 任务 C: TF = 0
- 任务 D: TF = 1
- 任务 E: TF = 0
- 任务 F: TF = 0
找出关键路径
关键路径上的任务总时差为 0,路径为 A -> C -> E -> F。
Java 实现
import java.util.*;public class CriticalPathMethod {static class Task {String id;int duration;List<String> dependencies;Task(String id, int duration, List<String> dependencies) {this.id = id;this.duration = duration;this.dependencies = dependencies;}}static class Graph {Map<String, Task> tasks;Map<String, List<String>> adjList;Map<String, Integer> earliestStart;Map<String, Integer> earliestFinish;Map<String, Integer> latestStart;Map<String, Integer> latestFinish;Map<String, Integer> totalFloat;Map<String, Integer> freeFloat;Graph(List<Task> taskList) {tasks = new HashMap<>();adjList = new HashMap<>();earliestStart = new HashMap<>();earliestFinish = new HashMap<>();latestStart = new HashMap<>();latestFinish = new HashMap<>();totalFloat = new HashMap<>();freeFloat = new HashMap<>();for (Task task : taskList) {tasks.put(task.id, task);adjList.put(task.id, new ArrayList<>());earliestStart.put(task.id, 0);earliestFinish.put(task.id, 0);latestStart.put(task.id, Integer.MAX_VALUE);latestFinish.put(task.id, Integer.MAX_VALUE);totalFloat.put(task.id, 0);freeFloat.put(task.id, 0);}}void addEdge(String from, String to) {adjList.get(from).add(to);}void calculateEarliestTimes() {for (String task : tasks.keySet()) {calculateEarliestTimes(task);}}int calculateEarliestTimes(String task) {if (earliestFinish.get(task) > 0) {return earliestFinish.get(task);}int duration = tasks.get(task).duration;int es = 0;for (String dep : tasks.get(task).dependencies) {es = Math.max(es, calculateEarliestTimes(dep));}earliestStart.put(task, es);earliestFinish.put(task, es + duration);return earliestFinish.get(task);}void calculateLatestTimes() {int maxTime = Collections.max(earliestFinish.values());for (String task : tasks.keySet()) {latestFinish.put(task, maxTime);}for (String task : tasks.keySet()) {calculateLatestTimes(task);}}int calculateLatestTimes(String task) {int duration = tasks.get(task).duration;int lf = latestFinish.get(task);for (String neighbor : adjList.get(task)) {lf = Math.min(lf, calculateLatestTimes(neighbor) - duration);}latestStart.put(task, lf - duration);latestFinish.put(task, lf);return latestStart.get(task);}void calculateTotalAndFreeFloat() {for (String task : tasks.keySet()) {totalFloat.put(task, latestStart.get(task) - earliestStart.get(task));int minFreeFloat = Integer.MAX_VALUE;for (String neighbor : adjList.get(task)) {minFreeFloat = Math.min(minFreeFloat, earliestStart.get(neighbor) - earliestFinish.get(task));}freeFloat.put(task, minFreeFloat == Integer.MAX_VALUE ? totalFloat.get(task) : minFreeFloat);}}List<String> getCriticalPath() {List<String> criticalPath = new ArrayList<>();for (String task : tasks.keySet()) {if (totalFloat.get(task) == 0) {criticalPath.add(task);}}return criticalPath;}}public static void main(String[] args) {List<Task> tasks = Arrays.asList(new Task("A", 3, Collections.emptyList()),new Task("B", 2, Arrays.asList("A")),new Task("C", 4, Arrays.asList("A")),new Task("D", 2, Arrays.asList("B")),new Task("E", 1, Arrays.asList("C")),new Task("F", 3, Arrays.asList("D", "E")));Graph graph = new Graph(tasks);graph.addEdge("A", "B");graph.addEdge("A", "C");graph.addEdge("B", "D");graph.addEdge("C", "E");graph.addEdge("D", "F");graph.addEdge("E", "F");graph.calculateEarliestTimes();graph.calculateLatestTimes();graph.calculateTotalAndFreeFloat();System.out.println("Earliest Start Times: " + graph.earliestStart);System.out.println("Earliest Finish Times: " + graph.earliestFinish);System.out.println("Latest Start Times: " + graph.latestStart);System.out.println("Latest Finish Times: " + graph.latestFinish);System.out.println("Total Float: " + graph.totalFloat);System.out.println("Free Float: " + graph.freeFloat);System.out.println("Critical Path: " + graph.getCriticalPath());}
}
相关文章:

图的关键路径算法
关键路径算法(Critical Path Method, CPM)是一种用于项目管理和调度的技术,通过分析项目任务的最早开始时间、最晚完成时间和总时差,找出项目中关键的任务路径。这条关键路径决定了项目的最短完成时间,因为关键路径上的…...

模型情景制作-冰镇啤酒
夏日炎炎,当我们在真实世界中开一瓶冰镇啤酒的时候,我们也可以为模型世界中的人物添加一些冰镇啤酒。 下面介绍一种快速酒瓶制造方法,您只需要很少工具: 截取尽量直的流道(传说中的板件零件架),将其夹在您的…...

网页实现黑暗模式的几种方式
## 实现暗黑模式的最佳方式 在现代网页设计中,暗黑模式已成为提高用户体验的重要功能。实现暗黑模式不仅可以减少用户眼睛的疲劳,还能在某些情况下节省设备电量。本文将介绍实现暗黑模式的几种最佳方式。 ### 使用 CSS 变量 (CSS Custom Properties) …...
VMware Workstation环境下,邮件(E-Mail)服务的安装配置,并用Windows7来验证测试
需求说明: 某企业信息中心计划使用IP地址17216.11.0用于虚拟网络测试,注册域名为xyz.net.cn.并将172.16.11.2作为主域名的服务器(DNS服务器)的IP地址,将172.16.11.3分配给虚拟网络测试的DHCP服务器,将172.16.11.4分配给虚拟网络测试的web服务器,将172.16.11.5分配给FTP服务器…...

《信号与系统》复试建议
目录 第一章 绪论 第二章 连续时间系统的时域分析 第三章 傅立叶变换(重点) 第四章 拉普拉斯变换(重点) 第五章 傅立叶变换在通信系统中的应用 第六章 信号的矢量空间分析 第七章 离散时间系统的时域分析 第八章 Z变换与离…...

代码随想录训练营Day45
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、打家劫舍二、打家劫舍2三、打家劫舍3 前言 提示:这里可以添加本文要记录的大概内容: 今天是跟着代码随想录刷题的第45天ÿ…...
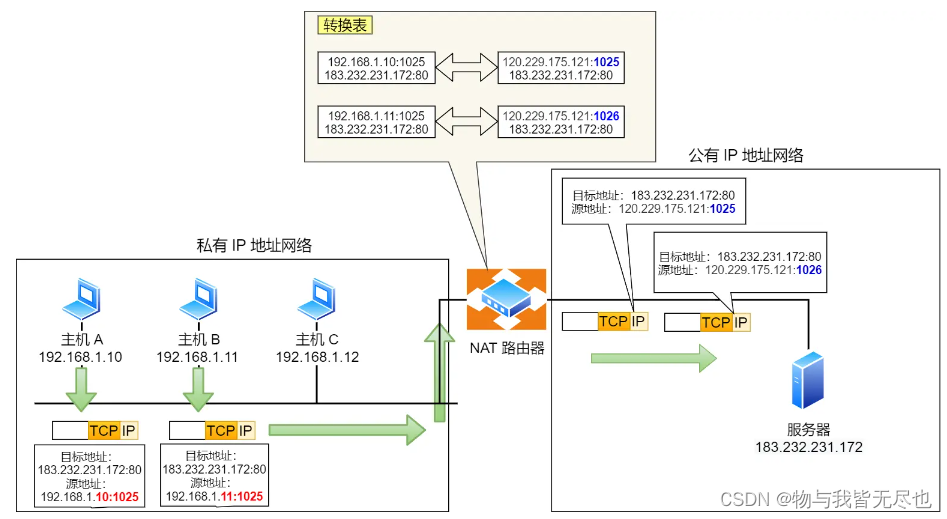
NAT和内网穿透
NAT(Network Address Translation,网络地址转换)是一种广泛应用于计算机网络的技术,其主要目的是为了解决IPv4地址空间的短缺问题,并且增强网络安全。NAT技术允许一个私有网络内的多个设备共享一个或几个全局唯一的公共…...
)
android | 声明式编程!(笔记)
https://www.jianshu.com/p/c133cb7cac21 讲的不错 命令式UI (how to do) 声明式UI (what to do) what to do 也许有人会说Data Binding不是可以让XML自己"动"起来吗?没有错,Data Binding其实就是Compose诞生之前的一种声明式U方案,谷歌曾…...
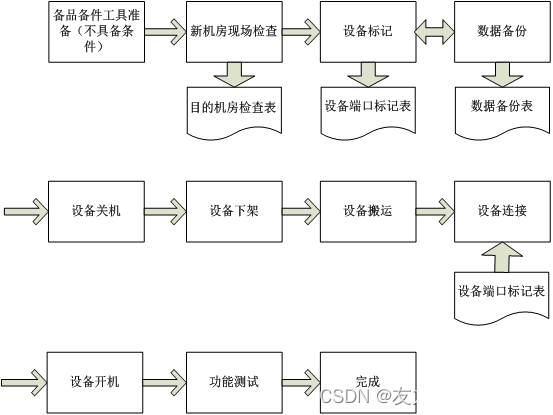
友力科技IDC机房搬迁方案流程分享
机房搬迁流程 系统搬迁实施流程包括:准备、拆卸、装运、安装、调试等五个流程,具体如下: 准备:包括相关人员和设备准备、新机房环境准备、网络环境、备份、现场所有设备打标签、模块、设备准备等准备工作。拆卸:主要只核心设备下…...
仿迪恩城市门户分类信息网discuz模板
Discuz x3.3模板 仿迪恩城市门户分类信息网 (GBK) Discuz模板 仿迪恩城市门户分类信息网(GBK)...
Windows 注册表是什么?如何备份注册表?
Windows注册表(Windows Registry)是微软Windows操作系统中的一个重要组件,用于存储系统和应用程序的配置信息和选项。下面就给大家详细讲解一下什么是注册表。 注册表的概念 Windows 注册表是一个集中管理的数据库,存储了系统、…...

B+树与索引解析
文章目录 B树与索引简介几个关键点应用案例场景描述索引创建查询操作更新操作并发处理 Python代码示例 B树与索引简介 B树是一种在计算机科学中广泛使用的自平衡的树数据结构,它能保持数据排序,并且搜索、插入和删除操作的时间复杂度都是O(log n)。B树被…...

华为认证hcna题库背诵技巧有哪些?hcna和hcia有什么区别?
大家都知道华为认证hcna是有题库供考生刷题备考的,但题库中海量的题目想要在短时间背诵下来可并不是一件容易的事情,这就需要我们掌握一定的技巧才行。华为认证hcna题库背诵技巧有哪些? hcna和hcna这二者又有什么区别呢?今天的文章将为大家进行详细解…...

【常用报文状态码】
常见的报文状态码如下 200 OK:客户端请求成功。 301 Moved Permanently:表示请求的资源已经被永久移动到了新的URL上; 302 Found:表示请求的资源已经被临时移动到了新的URL上; 304 Not Modified:表示客户…...
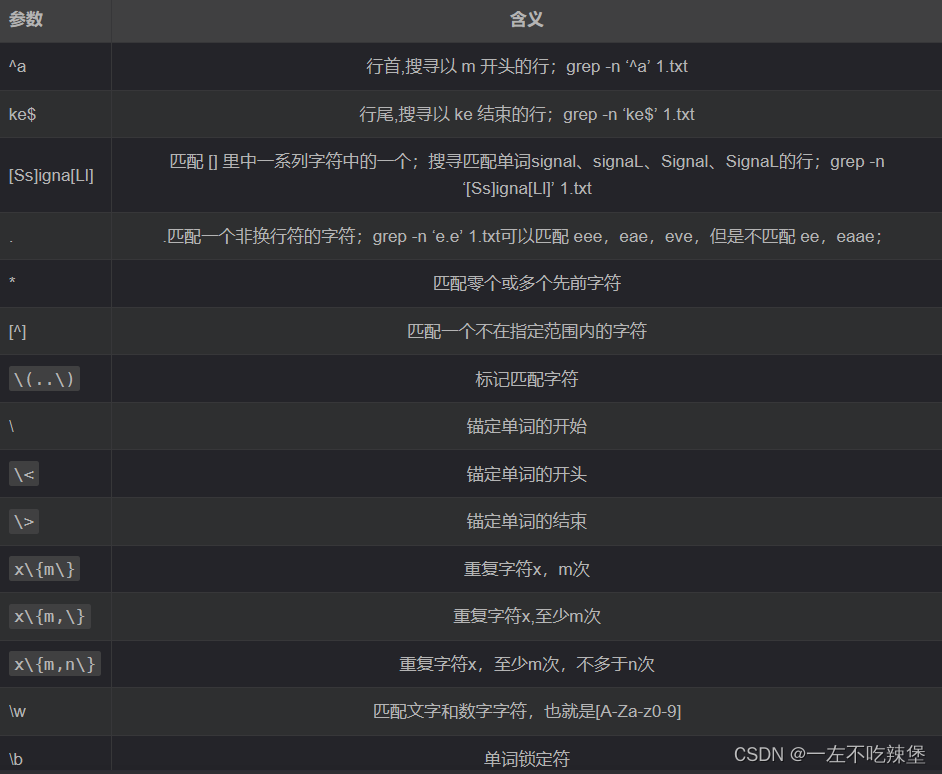
Linux命令详解
1.目录结构 2.history游览历史 3.命令行中的ctrl组合键 4.列出目录的内容 5.修改文件权限chmod 6.文件内容查看 文件管理 7.输出重定向:> 8.管道:| 9.清屏:clear 10.显示当前路径:pwd 11.创建目录:mkdir…...
在阿里云使用Docker部署MySQL服务,并且通过IDEA进行连接
阿里云使用Docker部署MySQL服务,并且通过IDEA进行连接 这里演示如何使用阿里云来进行MySQL的部署,系统使用的是Linux系统 (Ubuntu)。 为什么使用Docker? 首先是因为它的可移植性可以在任何有Docker环境的系统上运行应用,避免了在不通操作系…...
实现技巧)
Spring Boot中的国际化(i18n)实现技巧
Spring Boot中的国际化(i18n)实现技巧 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在开发多语言支持的应用程序时,国际化…...

vite-ts-cesium项目集成mars3d修改相关的包和配置参考
如果vite技术栈下使用原生cesium,请参考下面文件的包和配置修改,想用原生创建的viewer结合我们mars3d的功能的话。 1. package.json文件 "dependencies": {"cesium": "^1.103.0","mars3d": "^3.7.18&quo…...

「树莓派入门」树莓派基础04-VNC连接与配置静态IP
一、VNC连接配置 1. 启用VNC服务 在树莓派上,通过 raspi-config 工具启用VNC服务: sudo raspi-config在配置界面中选择 “Interfacing Options”,然后选择 “VNC” 并启用它。 2. 连接到VNC服务器 在电脑端安装VNC客户端,如V…...
JAVA编程题期末题库【中】
8.计算邮资 程序代码: public static void main(String[] args) {// 计算邮资//if多分支语句//创建对象java.util.Scanner inputnew java.util.Scanner(System.in); //提示输入用户,输入邮件的重量System.out.println("邮件的重量:");int wei…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
