状态压缩DP——AcWing 327. 玉米田
状态压缩DP
定义
状态压缩 DP 是一种通过二进制压缩状态的动态规划算法。它通过使用位运算来加速状态的转移和计算,从而提高算法的效率。
注意事项
- 数据范围:状态压缩 DP 通常适用于数据范围较小的问题,因为它需要使用二进制来表示状态,所以状态数量会随着数据范围的增加而呈指数级增长。
- 位运算:位运算在状态压缩 DP 中非常常用,需要熟练掌握位运算的基本操作,如与、或、异或、左移、右移等。
- 状态表示:选择合适的状态表示方式非常重要,需要根据问题的特点和要求来设计状态。一般来说,可以使用二进制数来表示状态,其中每一位表示一个元素的选择情况。
- 状态转移:状态转移是状态压缩 DP 的核心,需要根据问题的逻辑来设计状态转移方程。在状态转移过程中,需要注意边界情况和特殊情况的处理。
- 初始化:正确的初始化状态非常重要,需要根据问题的要求来初始化状态。一般来说,可以将初始状态设置为全 0 或全 1。
- 空间复杂度:状态压缩 DP 通常需要使用较大的空间来存储状态,因此需要注意空间复杂度的控制。可以通过滚动数组、压缩状态等方式来减少空间的使用。
解题思路
- 确定状态:根据问题的要求,确定需要使用的状态。状态可以是一个整数、一个二进制数或一个数组等。
- 设计状态转移方程:根据问题的逻辑,设计状态转移方程。状态转移方程描述了从一个状态到另一个状态的转移方式。
- 初始化状态:根据问题的要求,初始化状态。初始化状态通常是一个边界情况或特殊情况。
- 进行状态转移:使用状态转移方程,从初始状态开始,逐步进行状态转移,计算出每个状态的值。
- 输出结果:根据问题的要求,输出最终的结果。
状态压缩 DP 解决背包问题的一般步骤
- 确定状态:使用二进制数来表示背包的状态,每个物品的选择情况用一位二进制位表示,1 表示选择该物品,0 表示不选择。
- 设计状态转移方程:根据背包问题的逻辑,确定状态之间的转移关系。通常,状态转移方程会涉及到当前状态、上一个状态以及物品的选择情况。
- 初始化状态:根据问题的要求,初始化状态。通常,初始状态为全 0 或全 1。
- 进行状态转移:使用状态转移方程,从初始状态开始,逐步进行状态转移,计算出每个状态的值。
- 输出结果:根据问题的要求,输出最终的结果。
AcWing 327. 玉米田
题目描述
327. 玉米田 - AcWing题库
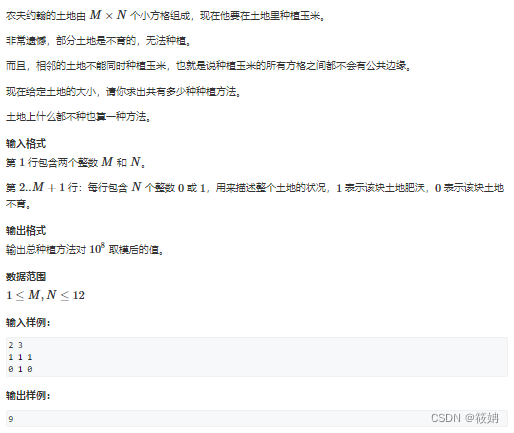
运行代码
#include <iostream>
#include <vector>
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;
int n, m;
int w[N];
vector<int> state;
vector<int> head[M];
int f[N][M];
bool check(int x)
{return !(x & x << 1);
}
int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 0; j < m; j ++){int t;cin >> t;w[i] += !t << j;}for(int i = 0; i < 1 << m; i ++)if(check(i)) state.push_back(i);for(int i = 0; i < state.size(); i ++)for(int j = 0; j < state.size(); j ++){int a = state[i], b = state[j];if(!(a & b)) head[i].push_back(j);}f[0][0] = 1; for(int i = 1; i <= n + 1; i ++)for(int j = 0; j < state.size(); j ++)if(!(state[j] & w[i]))for(auto k : head[j])f[i][j] = (f[i][j] + f[i - 1][k]) % mod;cout << f[n + 1][0] << endl;return 0;
}#include <iostream>
#include <vector>
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;
int n, m;
int w[N];
vector<int> state;
vector<int> head[M];
int f[N][M];
bool check(int x)
{return !(x & x << 1);
}
int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 0; j < m; j ++){int t;cin >> t;w[i] += !t << j;}for(int i = 0; i < 1 << m; i ++)if(check(i)) state.push_back(i);for(int i = 0; i < state.size(); i ++)for(int j = 0; j < state.size(); j ++){int a = state[i], b = state[j];if(!(a & b)) head[i].push_back(j);}f[0][0] = 1; for(int i = 1; i <= n + 1; i ++)for(int j = 0; j < state.size(); j ++)if(!(state[j] & w[i]))for(auto k : head[j])f[i][j] = (f[i][j] + f[i - 1][k]) % mod;cout << f[n + 1][0] << endl;return 0;
}代码思路
- 首先读入行数
n和列数m以及土地的状况,将不可种植的情况转化为一个整数表示。 - 通过
check函数判断一个状态是否满足相邻位没有同时为 1 的条件,将满足条件的状态存入state向量。 - 构建状态之间的关联关系,将没有冲突的状态对存入
head数组。 - 然后通过动态规划,从第一行开始逐步计算每个状态下的种植方法数,利用之前的状态和关联关系进行递推。
改进思路
- 可以考虑对一些重复的计算进行缓存或优化,提高效率。
- 代码的结构和逻辑可以进一步整理和优化,增强可读性。
改进代码
#include <iostream>
#include <vector>
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;int n, m;
int w[N];
vector<int> state;
vector<int> head[M];
int f[N][M];bool check(int x) {return!(x & x << 1);
}void init() {for(int i = 0; i < 1 << m; i ++)if(check(i)) state.push_back(i);for(int i = 0; i < state.size(); i ++)for(int j = 0; j < state.size(); j ++) {int a = state[i], b = state[j];if(!(a & b)) head[i].push_back(j);}
}int main() {cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 0; j < m; j ++) {int t;cin >> t;w[i] +=!t << j;}init();f[0][0] = 1; for(int i = 1; i <= n + 1; i ++)for(int j = 0; j < state.size(); j ++)if(!(state[j] & w[i]))for(auto k : head[j])f[i][j] = (f[i][j] + f[i - 1][k]) % mod;cout << f[n + 1][0] << endl;return 0;
}相关文章:

状态压缩DP——AcWing 327. 玉米田
状态压缩DP 定义 状态压缩 DP 是一种通过二进制压缩状态的动态规划算法。它通过使用位运算来加速状态的转移和计算,从而提高算法的效率。 注意事项 数据范围:状态压缩 DP 通常适用于数据范围较小的问题,因为它需要使用二进制来表示状态&a…...

kafka(二)安装部署(2)windows
目录 一、前提 1、jdk 2、Zookeeper 2.1、解压 2.2、创建data文件夹 2.3、配置文件 2.4、添加环境变量 2.5、启动zk:zkServer 2.6、客户端 3、Scala 3.1、下载安装 3.2、配置环境变量 3.3、验证是否安装成功 二、kafka下载安装 1、下载 2、安装 2.1…...
)
aliplayer Server returned 403 Forbidden (access denied)
最近在接入阿里云播放器的sdk,项目的播放地址是m3u8的,h265的url 输入播放源以后播放报错,提示403,拒绝访问,起初以为是crt路径问题和key的问题,然后检查了以后没问题,后来又看了一下是不是白名单的问题,但是项目资源没通过阿里云平台存储 AVPUrlSource *source [[AVPUrlSou…...
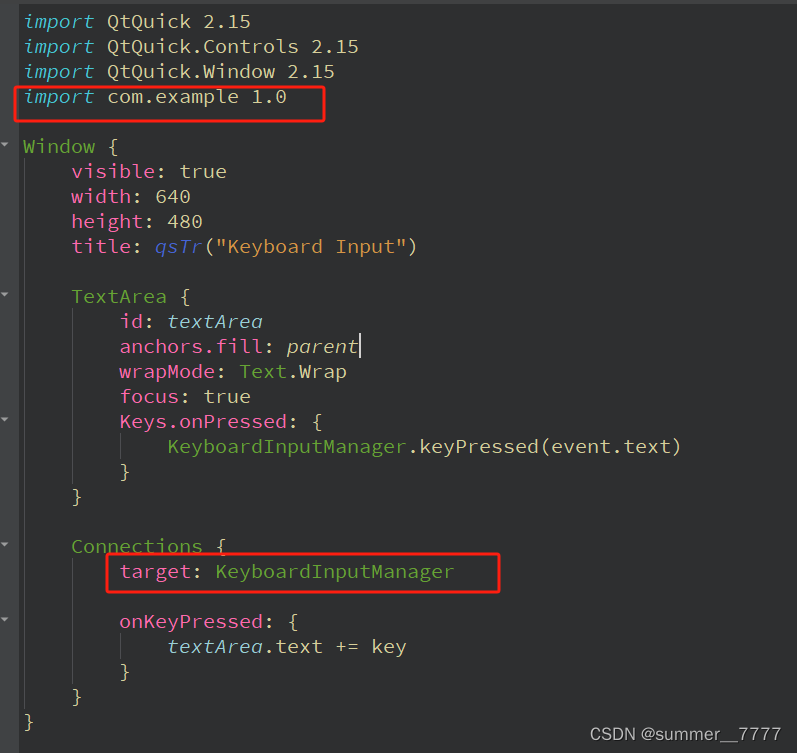
单例模式(下)
文章目录 文章介绍步骤安排及单例讲解step1:注册单例类型(main.cpp)step2:定义类和私有构造函数(keyboardinputmanager.h)step3:(keyboardinputmanager.cpp)step4:在qml中…...

合约期VS优惠期,搞明白他们的区别才能避免很多坑!
在购买流量卡时,相信大家也都发现了,市面上的不少套餐都是有合约期和优惠期的,尤其是联通和移动,那么,什么是合约期?什么又是优惠期呢? 其实,目前很多在网上办理的大流量卡都是有…...
在Scala中的实践与探索)
函数式反应式编程(FRP)在Scala中的实践与探索
函数式反应式编程(Functional Reactive Programming,简称FRP)是一种编程范式,它结合了函数式编程(Functional Programming,FP)的声明式特性和反应式编程(Reactive Programming&#…...

NGINX配置web文件服务
一、需求描述 系统需要提供文件(pdf、图片)等上传后支持预览功能。 二、实现方式 2.1 文件权限配置 chmod arwx -R public/chmod 是更改文件权限的命令。-R 是递归选项,表示更改目录及其所有子目录和文件的权限。arwx 是权限设置…...

deepspeed docker集群实现多机多卡训练----问题记录及解决方案资源汇总
. Docker中实现Deepspeed多机多卡训练 【掘金-雨田君的记事本】docker容器中deepspeed多机多卡集群分布式训练大模型 . 问题记录及解决方案资源汇总 问题1:deepspeed socketStartConnect: Connect to 172.18.0.3<54379> failed : Software caused connectio…...

恢复 IntelliJ IDEA 中消失的菜单栏
要恢复 IntelliJ IDEA 中消失的菜单栏,可以按照以下简单步骤操作: 使用快捷键打开搜索:首先,双击 Shift 键打开全局搜索对话框。 搜索“Menu”:在搜索框中输入 menu,然后从搜索结果中选择与“Main Menu”相…...

漏洞利用开发基础学习记录
文章目录 简介Win32缓冲区溢出内容难点 SEH 溢出内容难点 Egg Hunters内容难点 Unicode 溢出内容难点 x86-64 缓冲区溢出内容难点 参考资料 简介 本文基于ERC.Xdbg漏洞分析文章进行初步归纳整理,主要有Win32 缓冲区溢出、SEH 溢出、Egg Hunters、Unicode 溢出、x86…...

云通SIPX,您的码号资源智能调度专家!
在数字化转型的浪潮中,号码资源作为企业与客户沟通的重要桥梁,其管理效率直接关系到企业运营的成败。随着运营商对号码资源管理的规范化和精细化,企业对高效、智能的号码资源管理需求日益增长,以实现对外呼叫的降本增效。 一、什么…...

04-Mysql 索引,事务
MySQL 索引介绍 索引是一个排序的列表,在这个列表中存储着索引的值和包含这个值的数据所在行的物理地址。在数据十分庞大的时候,索引可以大大加快查询的速度。这是因为使用索引后可以不用扫描全表来定位某行的数据,而是先通过索引表找到该行…...
U盘提示格式化怎么搞定?本文有5种方法(内含教程)
U盘提示格式化是一种常见故障,即:当U盘插入电脑后,电脑上弹出对话框,提示该U盘需要格式化才能使用。 接触不良、文件系统损坏、热插拔、感染病毒、芯片损坏等原因都可能导致U盘出现此故障。这时点击“格式化”,大概率会…...
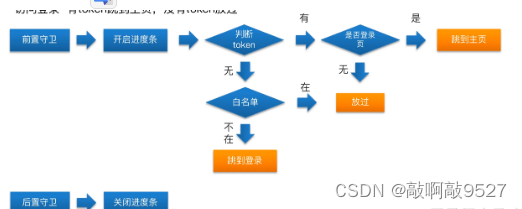
day02-登录模块-主页鉴权
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1.分析登录流程1.1传统思路是登录校验通过之后,直接调用接口,获取token之后,跳转到主页1.2vue-element-admin模板的登录思路&…...

git rebase的使用
没有排版,但是干货 因为项目要求,所以使用rebase指令 我使用的是rebase 的分支变基的功能 情景描述: 一共有两个分支:master owner 我在owner分枝上开发,有好多次commit master上也有同事在正常commit, …...
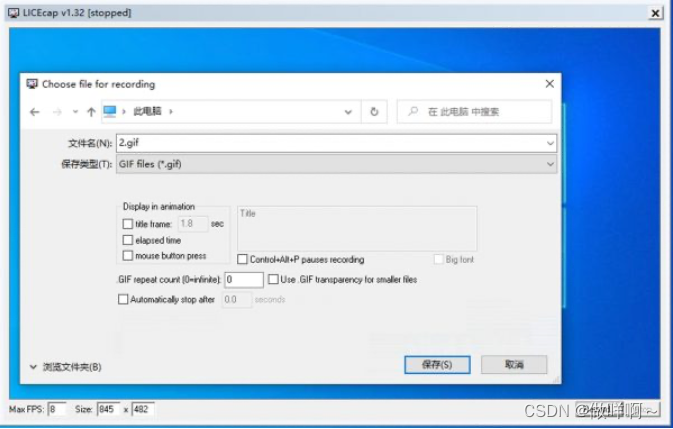
LICEcap-开源GIF 屏幕录制工具
LICEcap-开源GIF 屏幕录制工具 开源GIF 屏幕录制工具 下载可以访问:https://www.cockos.com/licecap/ 点击Record,开始录制 点击Stop,停止录制 点击Record,进入该页面 display in animation(在动画中显示) …...
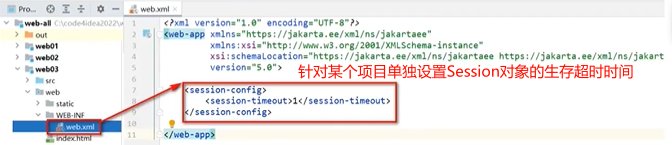
【Java Web】会话管理
目录 一、为什么需要会话管理? 二、会话管理机制 三、Cookie概述 四、HttpSession概述 4.1 HttpSession时效性 一、为什么需要会话管理? HTTP协议在设计之初就是无状态的,所谓无状态就是在浏览器和服务器之间的通信过程中,服务器并…...

RestTemplate修改默认转换器,使用FastJsonConverter
问题描述: 在使用RestTemplate发送POST请求时,发现发送的数据并未按配置的JSONField转换,导致服务方一直收不到参数 排查过程: 将itemList改成Items传输即可 原因分析: RestTemplate有默认的转换器,所以…...

什么是div移动指令?如何用vue自定义指令实现?
目录 一、Vue.js框架介绍二、vue自定义指令directive三、什么是div移动指令四、使用vue自定义指令directive写一个div移动指令 一、Vue.js框架介绍 Vue.js是一个用于构建用户界面的渐进式JavaScript框架。它设计得非常灵活,可以轻松地被集成到现有的项目中…...
Golang | Leetcode Golang题解之第187题重复的DNA序列
题目: 题解: const L 10 var bin map[byte]int{A: 0, C: 1, G: 2, T: 3}func findRepeatedDnaSequences(s string) (ans []string) {n : len(s)if n < L {return}x : 0for _, ch : range s[:L-1] {x x<<2 | bin[byte(ch)]}cnt : map[int]in…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
