买卖股票的最佳时机 I II III IV
121. 买卖股票的最佳时机

自己的思路:采用求最长连续子串和题目的思路
class Solution {public int maxProfit(int[] prices) {if(prices.length == 1) return 0;int[] nums = new int[prices.length - 1];for(int i = 0;i < prices.length - 1;i++){nums[i] = prices[i + 1] - prices[i];}int[] dp = new int[prices.length - 1];dp[0] = nums[0];int res = nums[0];for(int i = 1;i < dp.length;i++){dp[i] = Math.max(dp[i-1] + nums[i],nums[i]);res = Math.max(dp[i],res);}return res < 0 ? 0:res;}
}
贪心思路:
class Solution {public int maxProfit(int[] prices) {int low = Integer.MAX_VALUE;int result = 0;for(int i = 0;i < prices.length;i++){low = Math.min(low,prices[i]);result = Math.max(result,prices[i] - low);}return result;}
}
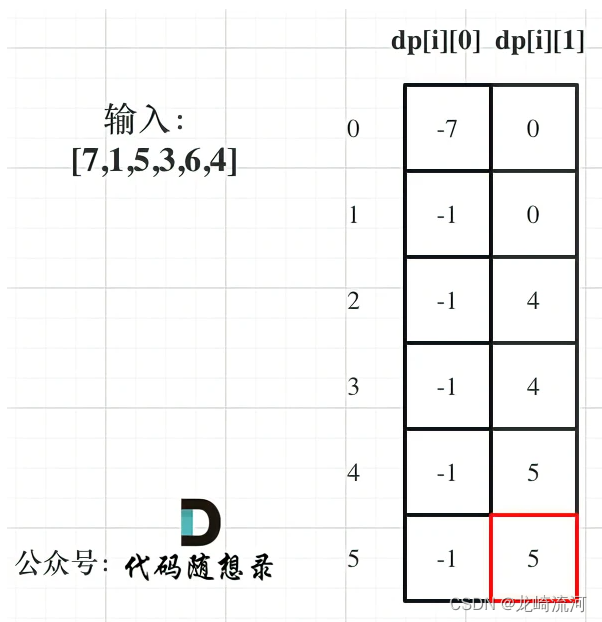
dp[i][0] dp[i][1] 表示第i天持有股票所得最多现金.
持有股票dp[i][0]:
1.之前就持有股票dp[i - 1][0]
2.现在刚持有也就是买入股票-prices[i]
不持有股票dp[i][1]:
1.之前就不持有股票dp[i - 1][1]
2.现在刚不持有也就是卖掉股票dp[i - 1][0] + prices[i]
class Solution {public int maxProfit(int[] prices) {if (prices == null || prices.length == 0) return 0;int length = prices.length;int[][] dp = new int[length][2];int result = 0;dp[0][0] = -prices[0];dp[0][1] = 0;for (int i = 1; i < length; i++) {dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);}return dp[length - 1][1];}
}

优化空间复杂度,不需要那么长的数组只需要两块。
class Solution {public int maxProfit(int[] prices) {if (prices == null || prices.length == 0) return 0;int length = prices.length;int[] dp = new int[2];int result = 0;dp[0] = -prices[0];dp[1] = 0;for (int i = 1; i < length; i++) {dp[0] = Math.max(dp[0], -prices[i]);dp[1] = Math.max(dp[0] + prices[i], dp[1]);}return dp[1];}
}

122. 买卖股票的最佳时机 II
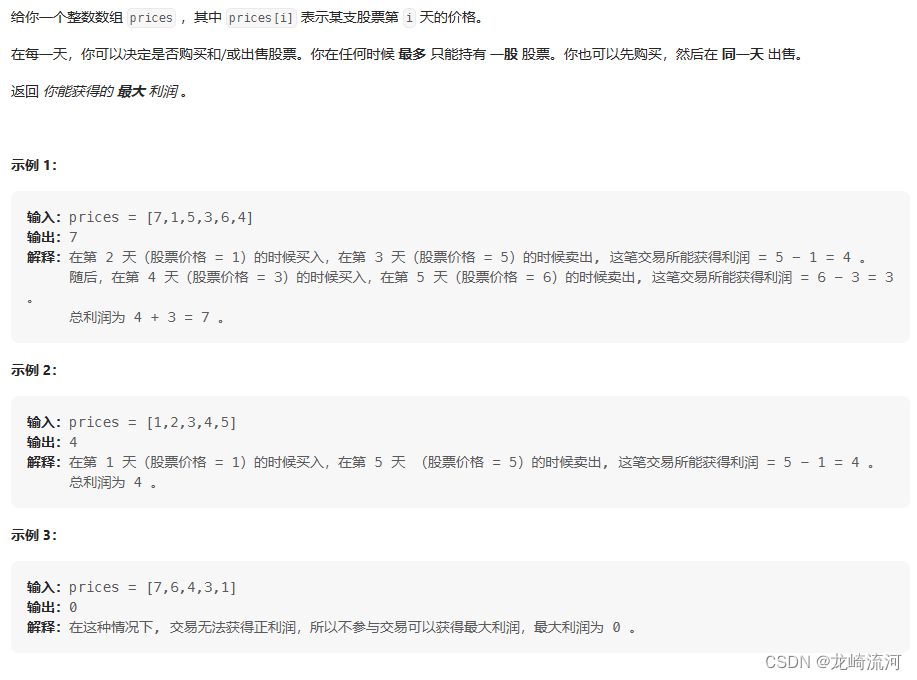
贪心算法:
class Solution {public int maxProfit(int[] prices) {if(prices.length == 1) return 0;int[] nums = new int[prices.length - 1];for(int i = 0;i < prices.length - 1;i++){nums[i] = prices[i + 1] - prices[i];}int result = 0;for(int i = 0;i < nums.length;i++){if(nums[i] > 0){result += nums[i];}}return result;}
}
而本题,因为一只股票可以买卖多次,所以当第i天买入股票的时候,所持有的现金可能有之前买卖过的利润。
那么第i天持有股票即dp[i][0],如果是第i天买入股票,所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即:dp[i - 1][1] - prices[i]。
dp[i-1][1] - price[i]是之前之前买卖过的利润 再减去当前买入
// 优化空间
class Solution {public int maxProfit(int[] prices) {int[] dp = new int[2];// 0表示持有,1表示卖出dp[0] = -prices[0];dp[1] = 0;for(int i = 1; i <= prices.length; i++){// 前一天持有; 既然不限制交易次数,那么再次买股票时,要加上之前的收益//与上一题唯一不同点dp[0] = Math.max(dp[0], dp[1] - prices[i-1]);// 前一天卖出; 或当天卖出,当天卖出,得先持有dp[1] = Math.max(dp[1], dp[0] + prices[i-1]);}return dp[1];}
}
123. 买卖股票的最佳时机 III

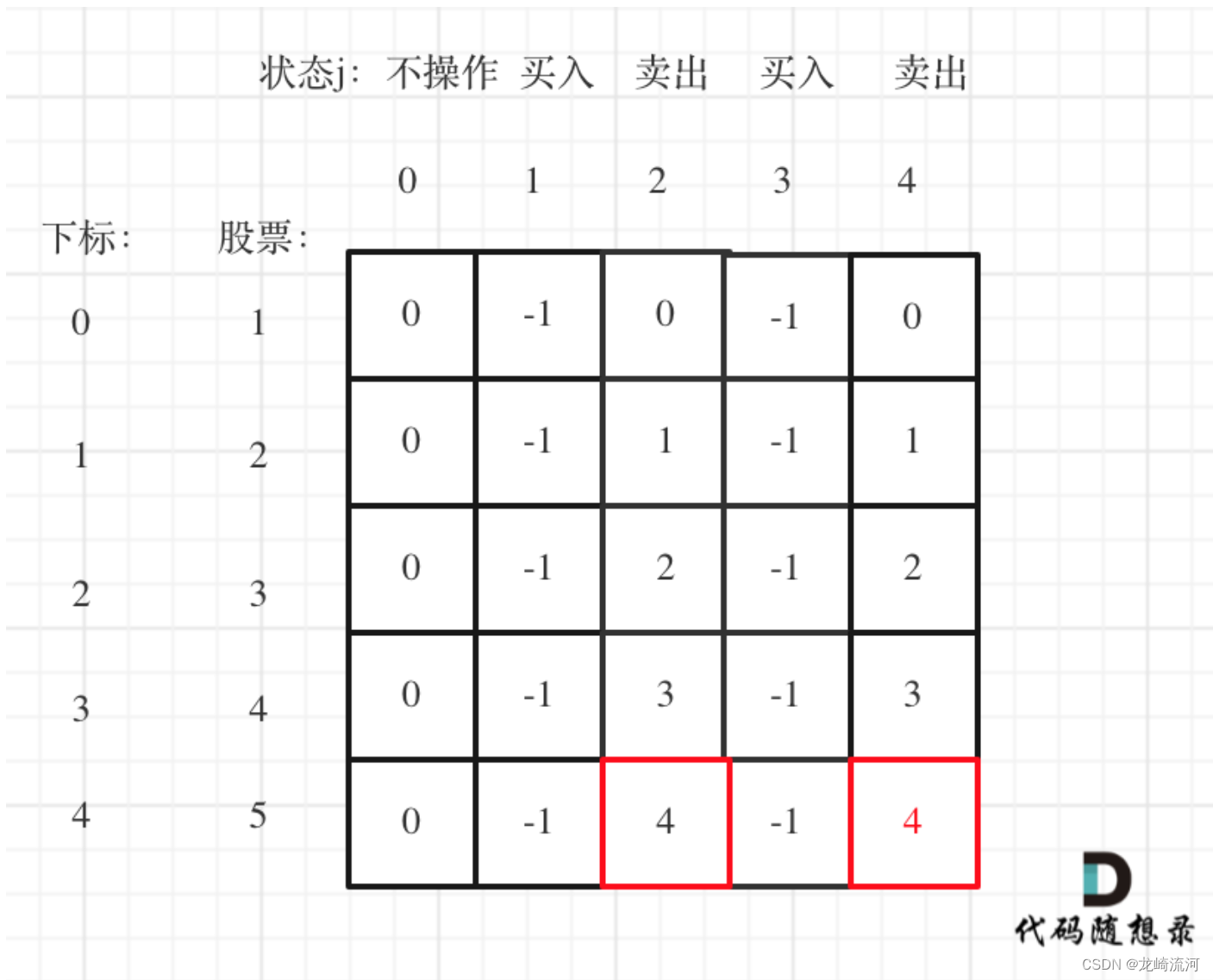
class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len == 0) return 0;int[][] dp = new int[len][5];dp[0][1] -= prices[0];dp[0][3] -= prices[0];for(int i = 1;i < prices.length;i++){dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]+prices[i]);dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]-prices[i]);dp[i][4] = Math.max(dp[i-1][4],dp[i-1][3]+prices[i]);}return dp[len - 1][4];}
}
class Solution {public int maxProfit(int[] prices) {int len = prices.length;if(len == 0) return 0;int[] dp = new int[5];dp[1] -= prices[0];dp[3] -= prices[0];for(int i = 1;i < len;i++){dp[1] = Math.max(dp[1],dp[0]-prices[i]);dp[2] = Math.max(dp[2],dp[1]+prices[i]);dp[3] = Math.max(dp[3],dp[2]-prices[i]);dp[4] = Math.max(dp[4],dp[3]+prices[i]);}return dp[4];}
}

188. 买卖股票的最佳时机 IV

和上一题思路一致
class Solution {public int maxProfit(int k, int[] prices) {int[] dp = new int[2*k + 1];for(int i = 0;i < 2*k + 1;i++){if(i % 2 == 1){dp[i] = -prices[0];}}for(int i = 0;i < prices.length;i++){for(int j = 1;j < 2*k+1;j++){int temp = j % 2 == 1?-prices[i]:prices[i];dp[j] = Math.max(dp[j],dp[j-1]+temp);}}return dp[2*k];}
}
相关文章:

买卖股票的最佳时机 I II III IV
121. 买卖股票的最佳时机 自己的思路:采用求最长连续子串和题目的思路 class Solution {public int maxProfit(int[] prices) {if(prices.length 1) return 0;int[] nums new int[prices.length - 1];for(int i 0;i < prices.length - 1;i){nums[i] prices[…...
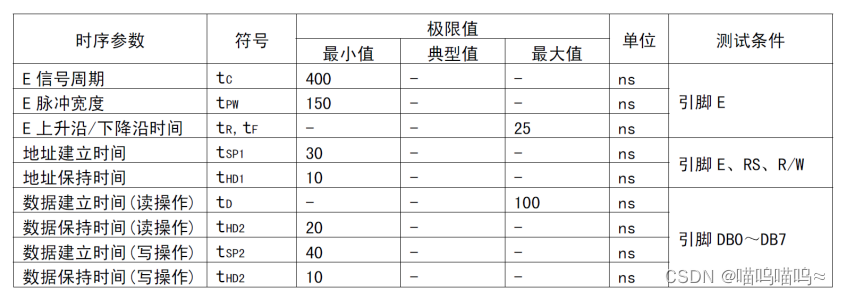
STM32—LCD1602
LCD1602(Liquid Crystal Display)是一种工业字符型液晶,能够同时显示 1602 即 32 字符(16列两行) 第 1 脚: VSS 为电源地 第 2 脚: VDD 接 5V 正电源 第 3 脚: VL 为液晶显示器对比度调整端,接正电源时对比度最弱,接地时对比度最…...

英雄算法学习路线
文章目录零、自我介绍一、关于拜师二、关于编程语言三、算法学习路线1、算法集训1)九日集训2)每月算法集训2、算法专栏3、算法总包四、英雄算法联盟1、英雄算法联盟是什么?2、如何加入英雄算法联盟?3、为何会有英雄算法联盟&#…...
【设计模式】备忘录模式和迭代器模式
备忘录模式和迭代器模式备忘录模式代码示例迭代器模式代码示例使用迭代器遍历集合的同时不能删除/增加元素总结备忘录模式 备忘录模式,也叫快照(Snapshot)模式。 在 GoF的《设计模式》⼀书中,备忘录模式是这么定义的:…...
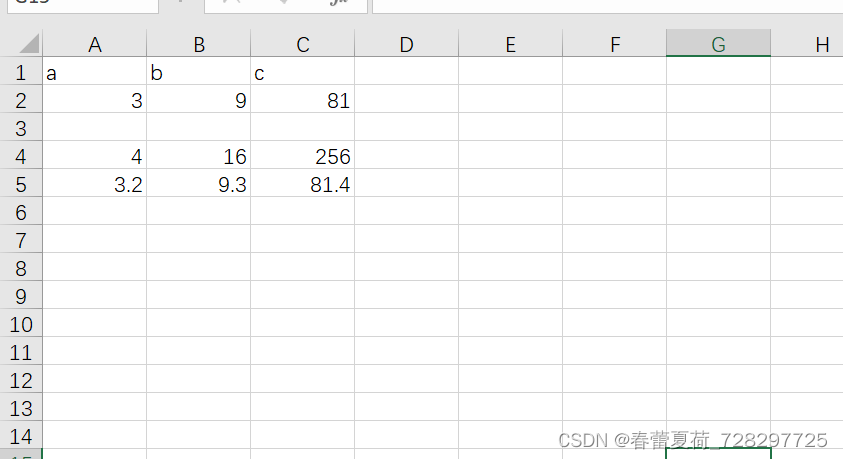
rapidcsv 写csv文件实例
csv实质是一个文本文件,可以使用rapidcsv写文件操作,如下实例: 第一行实质是从-1行开始,列是从0开始 #include "rapidcsv.h" #include <string> using namespace std; void CMFCApplication1Dlg::OnBnClickedBu…...

数据库--进阶篇--9--存储引擎
MySQL体系结构 索引是在引擎层,所以不同的存储引擎,它的索引结构不同。 存储引擎简介 存储引擎就是存储数据、建立所以、更新/查询数据等技术的实现方式。存储引擎是基于表的,而不是基于库的,所以存储引擎也可以被称为表类型。 …...

物品的管理的隐私政策
本应用尊重并保护所有使用服务用户的个人隐私权。为了给您提供更准确、更有个性化的服务,本应用会按照本隐私权政策的规定使用和披露您的个人信息。但本应用将以高度的勤勉、审慎义务对待这些信息。除本隐私权政策另有规定外,在未征得您事先许可的情况下…...

深度解析首个Layer3 链 Nautilus Chain,有何优势?
以流支付为主要概念的Zebec生态,正在推动流支付这种新兴的支付方式向更远的方向发展,该生态最初以Zebec Protocol的形态发展,并从初期的Solana进一步拓展至BNB Chian以及Near上。与此同时,Zebec生态也在积极的寻求从协议形态向公链…...

配对变量t检验
区别双变量t检验,见:https://mp.csdn.net/postedit/100640098 配对变量为两两相关的变量:如敷药前后体重变化。 要求:两变量服从正态分布。 SPSS演练 打开数据文件:ptest.sav 载地址:https://download.c…...

蓝桥杯三月刷题 第八天
文章目录💥前言😉解题报告💥分数🤔一、思路:😎二、代码:💥回文日期🤔一、思路:😎二、代码:💥迷宫🤔一、思路:😎二、代码&a…...

EXCEL技能点3-常用技能1
1 引用格式 公式中引用单元格或者区域时,引用的类型可分为以下三种: 绝对引用 相对引用 混合引用 在Excel里,每个单元格都有一个编码,就像人的身份证一样,在Excel里是按照行列进行编码,例如A1就是第一列的第一行。 那么我们想要引…...
)
经典分类模型回顾16-AlexNet实现垃圾分类(Tensorflow2.0版)
AlexNet是2012年由亚历克斯克里斯托夫(Alex Krizhevsky)等人提出的一种卷积神经网络结构,它在ImageNet图像识别比赛中获得了第一名,标志着卷积神经网络的崛起。 AlexNet的结构包括8层网络,其中前5层为卷积层ÿ…...

vue3使用vuex
第一步安装: package.json { "name": "demo", "version": "0.1.0", "private": true, "scripts": { "serve": "vue-cli-service serve", "build": "vue-c…...

Java面向对象:抽象类的学习
本文介绍了抽象类的基本语法概念,什么是抽象类. Java中抽象类的语法,抽象类的特性 抽象类的作用(抽象类和普通类的区别) 用抽象类实现多态… 抽象类的学习一.什么是抽象类二.抽象类语法三.抽象类的特性四.抽象类的作用五. 抽象类实现多态一.什么是抽象类 在面向对象的概念中&am…...
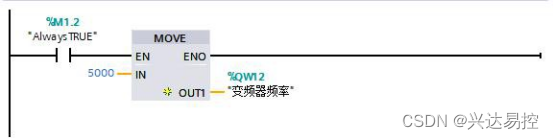
modbus转profinet网关连接5台台达ME300变频器案例
通过兴达易控Modbus转Profinet(XD-MDPN100)网关改善网络场景,变频器有掉线或数据丢失报警,影响系统的正常运行,将5台 ME300变频器modbus转Profinet到1200PLC,通过网关还可以实现Profinet转modbus RTU协议转…...
多校园SaaS运营智慧校园云平台源码 智慧校园移动小程序源码
智慧校园管理平台源码 智慧校园云平台源码 智慧校园全套源码包含:电子班牌管理系统、成绩管理系统、考勤人脸刷卡管理系统、综合素养评价系统、请假管理系统、电子班牌发布系统、校务管理系统、小程序移动端、教师后台管理系统、SaaS运营云平台(支持多学…...

用DQN实现Atari game(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 强化学习研究的是Agent和环境交互中如何学习最优策略,以获得最大收益。Agent需要能够观察环境(observe)所处的状态&…...

【JavaSE专栏11】Java的 if 条件语句
作者主页:Designer 小郑 作者简介:Java全栈软件工程师一枚,来自浙江宁波,负责开发管理公司OA项目,专注软件前后端开发(Vue、SpringBoot和微信小程序)、系统定制、远程技术指导。CSDN学院、蓝桥云…...

【opensea】opensea-js 升级 Seaport v1.4 导致的问题及解决笔记
一、opensea 协议升级导致旧包不能使用了 我使用的是 “opensea-js”: "^4.0.12” 版本当SDK。于2023年3月9日之后,不能使用了,需要升级到 Seaport v1.4 协议的包。 报错如下: Error: API Error 400: Please provide an OPEN order type when us…...
JS语法(扫盲)
文章目录一、初识JavaScript二、第一个JS程序JS代码的引入JS程序的输出三、语法变量使用动态类型内置类型运算符强类型语言&弱类型语言条件语句循环语句数组创建数组获取数组元素新增数组元素删除数组元素函数语法格式形参实参个数的问题匿名函数&函数表达式作用域作用…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
