【Python实战因果推断】4_因果效应异质性4
目录
Cumulative Gain
Target Transformation
Cumulative Gain
如果采用与累积效应曲线完全相同的逻辑,但将每个点乘以累积样本 Ncum/N,就会得到累积增益曲线。现在,即使曲线的起点具有最高的效果(对于一个好的模型来说),它也会因为相对规模较小而缩小。看一下代码,变化在于我现在每次迭代都会将效果乘以(行/大小)。此外,我还可以选择按 ATE 对曲线进行归一化处理,这就是为什么我还要在每次迭代时从效果中减去归一化处理的原因:
def cumulative_gain_curve(df, prediction, y, t,ascending=False, normalize=False, steps=100):effect_fn = effect(t=t, y=y)normalizer = effect_fn(df) if normalize else 0size = len(df)ordered_df = (df.sort_values(prediction, ascending=ascending).reset_index(drop=True))steps = np.linspace(size/steps, size, steps).round(0)effects = [(effect_fn(ordered_df.query(f"index<={row}"))-normalizer)*(row/size)for row in steps]return np.array([0] + effects)cumulative_gain_curve(test_pred, "cate_pred", "sales", "discounts")如果您不想费心实现所有这些函数,可以使用Python库为您处理这些问题。您可以简单地从fklearn因果模块中导入所有曲线及其AUC
from fklearn.causal.validation.auc import *
from fklearn.causal.validation.curves import *三种模型的累积增益和归一化累积增益如下图所示。在这里,CATE 排序较好的模型是曲线与代表 ATE 的虚线之间面积最大的模型: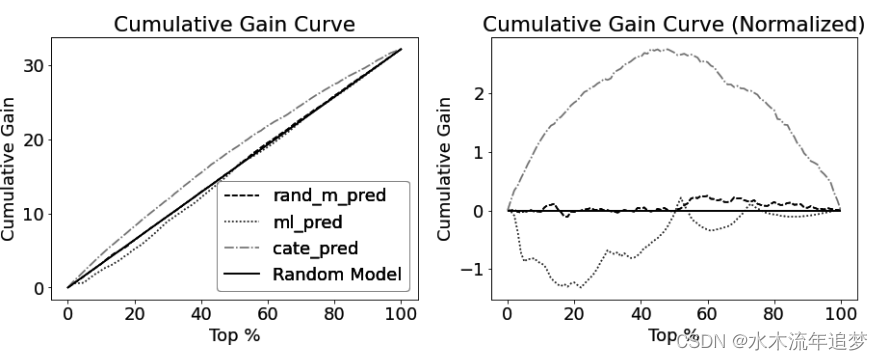 要将模型性能总结为一个数字,只需将归一化累积增益曲线上的数值相加即可。就 CATE 排序而言,数值最大的模型将是最佳模型。下面是您目前评估的三个模型的曲线下面积(AUC)。请注意,ML 模型的面积为负值,因为它对 CATE 进行了反向排序:
要将模型性能总结为一个数字,只需将归一化累积增益曲线上的数值相加即可。就 CATE 排序而言,数值最大的模型将是最佳模型。下面是您目前评估的三个模型的曲线下面积(AUC)。请注意,ML 模型的面积为负值,因为它对 CATE 进行了反向排序:
同样,您可以将模型的性能浓缩为一个数字,这一点也非常了不起,因为它可以自动选择模型。不过,虽然我很喜欢最后这条曲线,但在使用时还是需要注意一些问题。首先,在你看到的所有曲线中,重要的是要记住曲线中的每个点都是一个估计值,而不是地面真实值。它是对某一特定群体--有时是非常小的群体--的回归斜率的估计值。既然是回归估计值,它就取决于 T 和 Y 之间的关系是否正确。即使是随机化,如果治疗与干预结果之间的关系是一个对数函数,那么将效果估计为一条直线就会得出错误的结果。如果知道干预反应函数的形状,就可以将效应函数调整为 y~log(t) 的斜率,而不是 y~t。但要做到这一点,您需要知道正确的形状。
其次,这些曲线并不真正关心你是否正确地计算了 CATE。它们只关心排序是否正确。例如,如果您将任何一个模型的预测值减去-1,000,它们的累积增益曲线将保持不变。因此,即使您对 CATE 的估计存在偏差,这种偏差也不会在这些曲线中显示出来。现在,如果您只关心干预的优先次序,这可能不是问题。在这种情况下,排序就足够了。但是,如果您关心的是如何精确估算 CATE,那么这些曲线可能会误导您。如果您有数据科学背景,您可以将累积增益曲线与 ROC 曲线相提并论。同样,具有良好 ROC-AUC 的模型并不一定经过校准。
第三,或许也是最重要的一点,上述所有方法都需要无偏差数据。如果存在任何偏差,你对分组或 ATE 的效果估计都将是错误的。如果干预不是随机的,从理论上讲,你仍然可以使用这些评估技术,前提是你之前通过使用 IPW 的正交化等方法对数据进行了去偏差处理。不过,我对此有点怀疑。相反,我强烈建议你投资一些实验数据,哪怕只是一点点,只用于评估目的。这样,您就可以专注于效应异质性,而不必担心混杂因素的悄然出现。
因果模型评估是一个仍在发展中的研究领域。因此,它仍有许多盲点。例如,目前展示的曲线只能告诉您一个模型在 CATE 排序方面有多好。我还没有找到一个很好的解决方案来检查您的模型是否能正确预测 CATE。我喜欢做的一件事是在使用累积增益曲线的同时使用量子效应曲线图,因为前者能让我了解模型的校准程度,后者能让我了解模型对 CATE 的排序情况。至于归一化累积增益,它只是一个使可视化更容易的放大图。但我承认这并不理想。如果你正在寻找像 R2 或 MSE 这样的总结性指标--它们都是预测模型中常用的指标--我很遗憾地告诉你,在因果建模领域我还没有找到与它们类似的指标。不过,我还是找到了目标转换。
Target Transformation
X = ["C(month)", "C(weekday)", "is_holiday", "competitors_price"]y_res = smf.ols(f"sales ~ {'+'.join(X)}", data=test).fit().residt_res = smf.ols(f"discounts ~ {'+'.join(X)}", data=test).fit().residtau_hat = y_res/t_res接下来,您可以使用它来计算所有模型的MSE。注意我也如何使用前面讨论的权重:
from sklearn.metrics import mean_squared_errorfor m in ["rand_m_pred", "ml_pred", "cate_pred"]:wmse = mean_squared_error(tau_hat, test_pred[m],sample_weight=t_res**2)print(f"MSE for {m}:", wmse)根据这个加权MSE,再次,用于估计CATE的回归模型比其他两个表现更好。还有,这里还有一些有趣的东西。ML模型的性能比随机模型要差。这并不奇怪,因为ML模型试图预测Y,而不是τi。
只有当效应与结果相关时,预测 Y 才能很好地对 τi 进行排序或预测。这种情况一般不会发生,但在某些情况下可能会发生。其中有些情况在商业中相当常见,因此值得一探究竟。
相关文章:
【Python实战因果推断】4_因果效应异质性4
目录 Cumulative Gain Target Transformation Cumulative Gain 如果采用与累积效应曲线完全相同的逻辑,但将每个点乘以累积样本 Ncum/N,就会得到累积增益曲线。现在,即使曲线的起点具有最高的效果(对于一个好的模型来说&#x…...

大模型推理知识总结
一、大模型推理概念 大多数流行的only-decode LLM(例如 GPT-3)都是针对因果建模目标进行预训练的,本质上是作为下一个词预测器。这些 LLM 将一系列tokens作为输入,并自回归生成后续tokens,直到满足停止条件࿰…...

[笔记] keytool 导入服务器证书和证书私钥
背景 我当前手头已有一个服务器证书和对应的私钥,现在需要转换为 Java KeyStore 格式使用,找了一大圈才发现 keytool 无法直接导入服务器证书和私钥,当然证书可以直接导入,但是私钥是无法直接导入。找了一大圈发现可以先将服务器…...
【2024-热-办公软件】ONLYOFFICE8.1版本桌面编辑器测评
在今日快速发展的数字化办公环境中,选择一个功能全面且高效的办公软件是至关重要的。最近,我有幸体验了ONLYOFFICE 8.1版本的桌面编辑器,这款软件不仅提供了强大的编辑功能,还拥有众多改进,让办公更加流畅和高效。在本…...
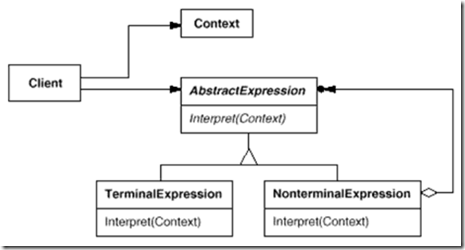
C# 23设计模式备忘
创建型模式:单例(Singleton)模式:某个类只能生成一个实例,该类提供了一个全局访问点供外部获取该实例,其拓展是有限多例模式。 原型(Prototype)模式:将一个对象作为原型&…...

STL中的迭代器模式:将算法与数据结构分离
目录 1.概述 2.容器类 2.1.序列容器 2.2.关联容器 2.3.容器适配器 2.4.数组 3.迭代器 4.重用标准迭代器 5.总结 1.概述 在之前,我们讲了迭代器设计模式,分析了它的结构、角色以及优缺点: 设计模式之迭代器模式-CSDN博客 在 STL 中&a…...

TCP、UDP详解
目录 1.区别 1.1 概括 1.2 详解 2.TCP 2.1 内容 2.2 可靠传输 2.2.1 确认应答 2.2.2 超时重传 2.2.3 连接管理 三次握手 四次挥手 2.2.4 滑动窗口 2.2.5 流量控制 2.2.6 拥塞控制 2.2.7 延时应答 2.2.8 捎带应答 2.2.9 面向字节流 2.2.10 异常情况的处理 1.…...
)
【脚本工具库】批量下采样图像(附源码)
在图像处理领域,我们经常需要对大批量图像进行下采样操作,以便减小图像的尺寸和文件大小,这对于节省存储空间和提高处理速度非常有帮助。手动操作不仅耗时,而且容易出错。为了解决这个问题,我们可以编写一个Python脚本…...

Web渗透:文件包含漏洞
Ⅱ.远程文件包含 远程文件包含漏洞(Remote File Inclusion, RFI)是一种Web应用程序漏洞,允许攻击者通过URL从远程服务器包含并执行文件;RFI漏洞通常出现在动态包含文件的功能中,且用户输入未经适当验证和过滤。接着我…...
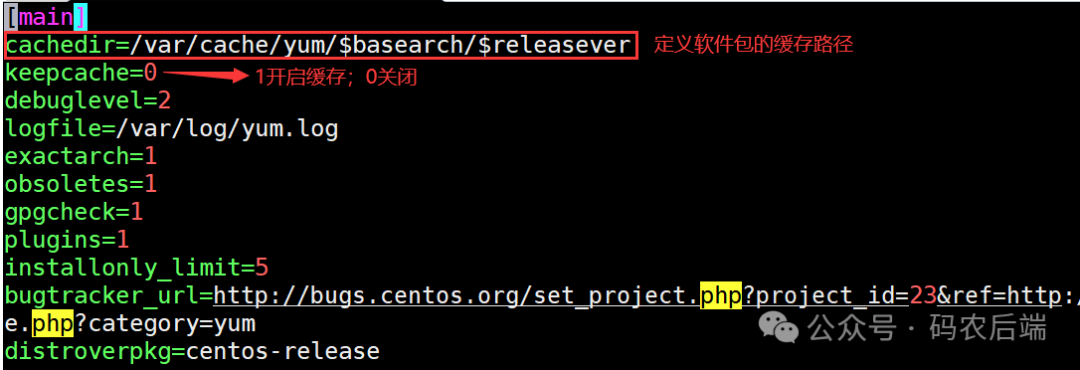
什么是yum源?如何对其进行配置?
哈喽,大家好呀!这里是码农后端。今天来聊一聊Linux下的yum源及其配置相关的内容。简单来说,yum源就相当于一个管理软件的工具,可以想象成一个很大的仓库,里面存放着各种我们所需要的软件包及其依赖。 一、Linux下软件包…...
Node.js全栈指南:认识MIME和HTTP
MIME,全称 “多用途互联网邮件扩展类型”。 这名称相当学术,用人话来说就是: 我们浏览一个网页的时候,之所以能看到 html 文件展示成网页,图片可以正常显示,css 样式能正常影响网页效果,js 脚…...
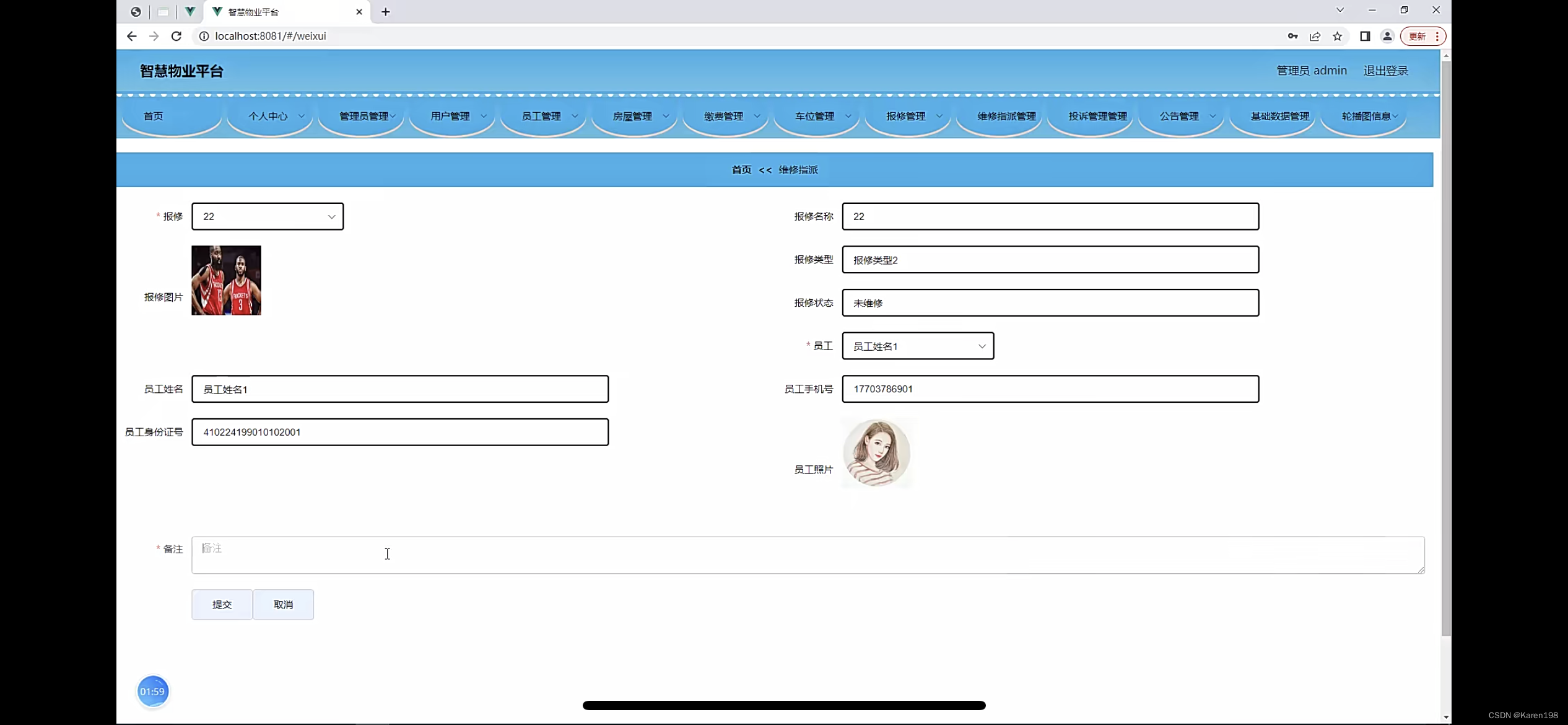
基于weixin小程序智慧物业系统的设计
管理员账户功能包括:系统首页,个人中心,管理员管理,用户管理,员工管理,房屋管理,缴费管理,车位管理,报修管理 工作人员账号功能包括:系统首页,维…...

成功解决TypeError: __call__() got an unexpected keyword argument ‘first_int‘
成功解决TypeError: __call__() got an unexpected keyword argument first_int 目录 解决问题 解决思路 解决方法 T1、直接调用原始函数 T2、检查装饰器实现 T3、使用不同的调用方式 解决问题 result = multiply(**arguments) File "D:\ProgramData\Anaconda3\Li…...

vue3用自定义指令实现按钮权限
1,编写permission.ts文件 在src/utils/permission.ts import type { Directive } from "vue"; export const permission:Directive{// 在绑定元素的父组件被挂载后调用mounted(el,binding){// el:指令所绑定的元素,可以用来直接操…...

Nuxt3:当前页面滚动到指定位置
在Nuxt 3中,如果你想让当前页面跳转到指定位置,可以使用scrollIntoView方法。你需要给目标位置的元素添加一个ref引用,然后通过程序调用该ref来执行滚动。 以下是一个简单的例子: <template><div><!-- 其他内容 …...
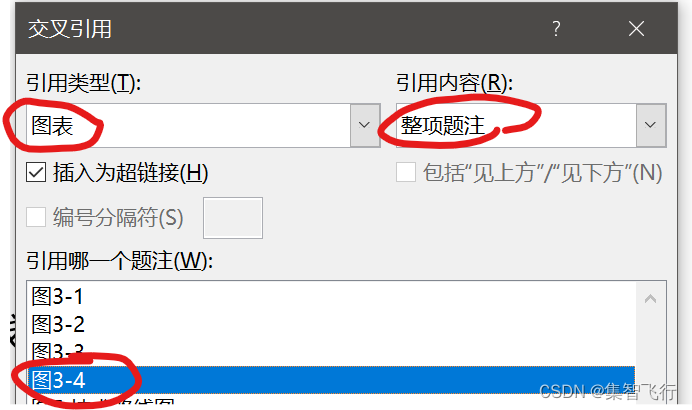
word图题表题公式按照章节编号(不用题注)
预期效果: 其中3表示第三章,4表示第3章里的第4个图。标题、公式编号也是类似的。 为了达到这种按照章节编号的效果,原本可以用插入题注里的“包含章节编号” 但实际情况是,这不仅需要一级标题的序号是用“开始->多级列表”自动…...

最小生成树模型
文章目录 题单最小生成树模型1.[最短网络(prim)](https://www.acwing.com/problem/content/1142/)2. [局域网(kruskul)](https://www.acwing.com/problem/content/1143/)3. [繁忙的都市](https://www.acwing.com/problem/content/1144/)4. [ 联络员 ](https://www.acwing.com/p…...

基于盲信号处理的声音分离-基于改进的信息最大化的ICA算法
基于信息最大化的ICA算法的主要依据是使输入端与输出端的互信息达到最大,且输出各个分量之间的相关性最小化,即输出各个分量之间互信息量最小化,其算法的系统框图如图所示。 基于信息最大化的ICA算法的主要依据是使输入端与输出端的互信息达到…...

如何在Qt Designer中管理QSplitter
问题描述 当按下按钮时,我希望弹出一个对话框,用户可以在其中选择内容并最终按下 ‘Ok’ 按钮。我想在这个对话框中放置一个 QSplitter,左侧面板将显示树状结构,右侧将显示其他内容。如何正确实现这一点? 从 Qt 的示…...

关于新零售的一些思考
本文作为2024上半年大量输入之后的核心思考之一。工作到一定阶段之后,思考的重要性越来越高,后续会把自己的个人思考记录在这个新系列《施展爱思考》。背景是上半年面临业务转型从电商到新零售,本文是相关大量输入之后的思考,对新…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
