Java【二叉搜索树和哈希表】详细图解 / 模拟实现 + 【Map和Set】常用方法介绍
文章目录
- 前言
- 一、二叉搜索树
- 1、什么是二叉搜索树
- 2、模拟实现二叉搜索树
- 2.1, 查找
- 2.2, 插入
- 2.3, 删除
- 3、性能分析
- 二、模型
- 三、哈希表
- 1、什么是哈希表
- 1.1, 什么是哈希冲突
- 1.2, 避免, 解决哈希冲突
- 1.2.1, 避免: 调节负载因子
- 1.2.2, 解决1: 闭散列(了解)
- 1.2.3, 解决2: 开散列/哈希桶(重点)
- 2、模拟实现哈希表
- 2.1, put --- 插入 Key-Value 键值对
- 2.1.1, resize --- 扩容, 调节负载因子
- 2.2, get ---获取 Key 的 Value 值
- 3、性能分析
- 四、Java 提供的 TreeMap 和 HashMap
- 1, Map 常用方法
- 1.1, 关于 Entry 的说明:
- 1.2, Entry 的常用方法:
- 2, Map 注意事项
- 3, TreeMap 和 HashMap 的区别
- 五、Java 提供的 TreeSet 和 HashSet
- 1, Set 常用方法
- 2, Set 注意事项
- 3, TreeSet和HashSet的区别
- 总结
前言
在 Java 的集合框架中, 除了 List 接口和 Queue 接口, 还有两个接口十分重要, 十分常用 : Map 和 Set
📌实现 Map 接口的有两个类: TreeMap 和 HashMap
📌实现 Set 接口的有两个类: TreeSet 和 HashSet
👉TreeMap 和 TreeSet 底层都是红黑树, 红黑树是在近似平衡的二叉搜索树 (VAL树) 上, 加之颜色变化及一些特殊性质的数据结构
👉HashMap 和 HashSet 底层都是哈希表
VAL树, 红黑树, B树,B+树的相关内容以后会在 [数据结构进阶] 专栏中分享
1️⃣先学习二叉搜索树, 并对其模拟实现
2️⃣再认识两种模型: 纯Key模型 和 Key-Value模型
3️⃣再学习哈希表, 并对其模拟实现
4️⃣5️⃣再学习Java中的 Map 和 Set
提示:是正在努力进步的小菜鸟一只,如有大佬发现文章欠佳之处欢迎评论区指点~ 废话不多说,直接发车~
一、二叉搜索树
1、什么是二叉搜索树
二叉搜索树(又称二叉排序树): 它或者是一棵空树,或者是具有以下性质的二叉树:
1️⃣若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
2️⃣若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
3️⃣它的左右子树也分别为二叉搜索树
说人话:
对每一颗树(子树)来说:
1️⃣根节点一定比左孩子结点大, 一定比右孩子结点小
2️⃣左树的所有结点都小于根节点, 右树所有结点都大于根节点
如图:
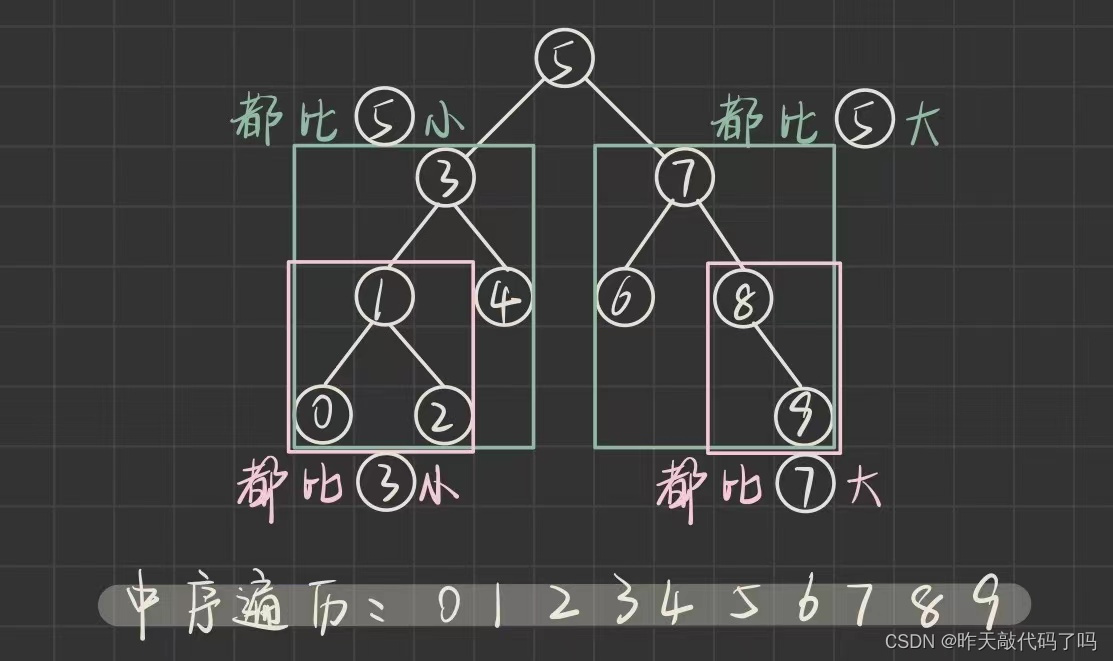
❗️❗️二叉搜索树还有一个特质: 二叉搜索树中序遍历序列一定是有序的
也可以利用这一点判断一棵树是否为二叉搜索树
二叉搜索树, 顾名思义就是一种主要用于查找的结构, 下面对二叉搜索树进行模拟实现, 主要实现 查找, 插入, 删除 操作
2、模拟实现二叉搜索树
首先写出二叉搜索树的成员属性和构造方法(和二叉树一致)
public class BinarySearchTree {static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}}public TreeNode root;
为了方便理解 + 代码易懂, 暂时不使用泛型以及封装
2.1, 查找
📌按照左小右大的规律, 依次进行结点之间的比较
📌因为目标数据一旦比当前结点的 val 大/小, 只可能出现在当前节点的某一侧, 另一侧的结点不需要比较, 所以不需要用递归遍历所有的结点, 利用循环, 沿着某一条路径走到 null 即可
📌循环中找到了返回该结点, 循环结束还没找到返回null
过程图解:

代码实现:
public TreeNode find(int val) {if (root == null) {return null;}TreeNode cur = root;while (cur != null) {if (val < cur.val) {cur = cur.left;} else if (val == cur.val) {return cur;} else {cur = cur.right;}}return null;}
2.2, 插入
经过每个结点的比较, 找到合适的位置插入即可
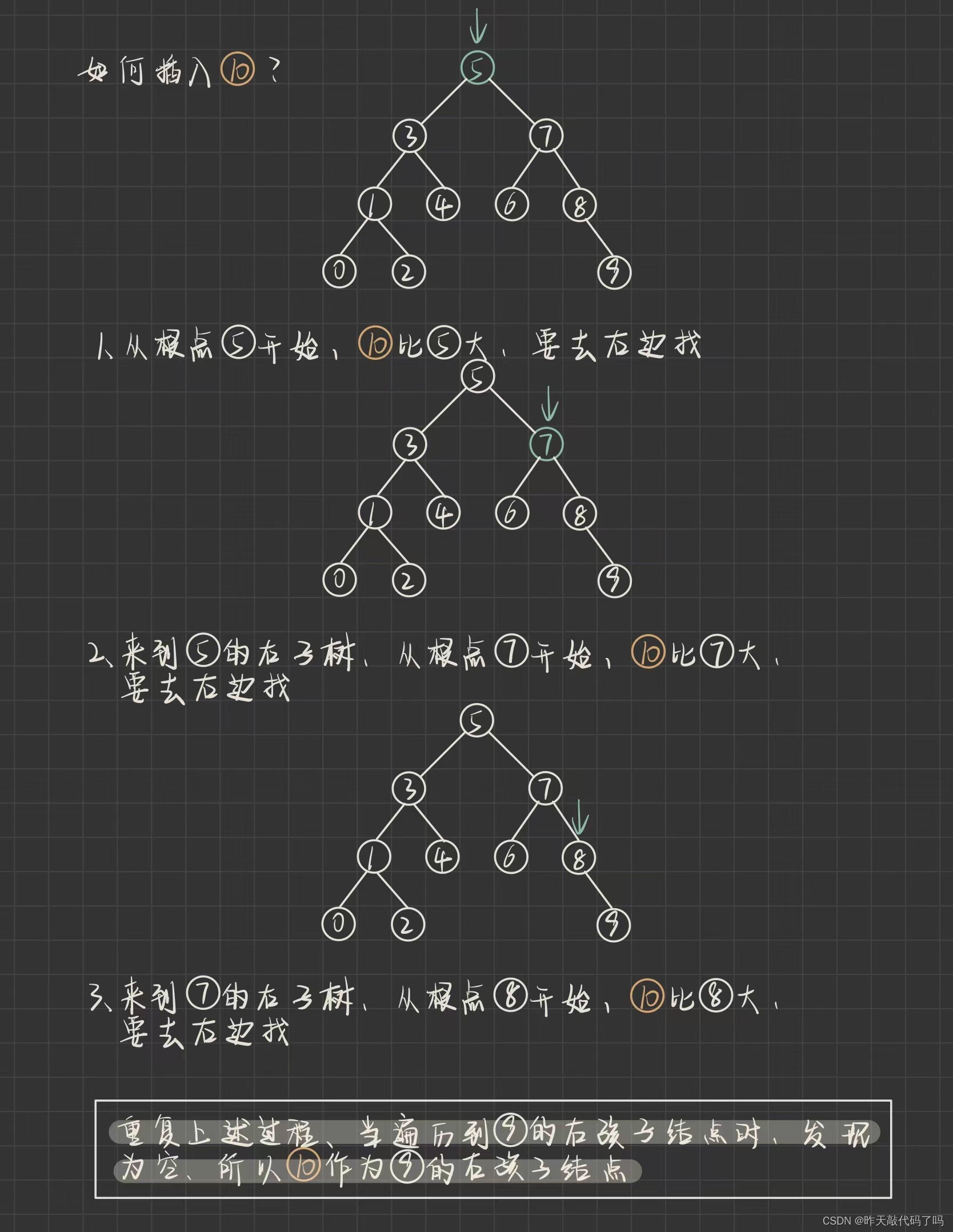
⚠️⚠️⚠️cur 遍历每一个结点时, 找到合适位置后, 此时 cur 已经是 null, 那么 cur 的父节点还能找到吗? 连父节点都找不到, 怎么插入(链接两个结点的引用)进去呢, 所以要记录上一个结点
退出循环找到合适位置后, 和父节点比较大小, 判断应该插入在父节点的左还是右
代码实现:
public void insert(int val) {if (root == null) {root = new TreeNode(val);}TreeNode cur = root;TreeNode parent = null;while (cur != null) {parent = cur;if (val < cur.val) {cur = cur.left;} else if (val == cur.val) {return;} else {cur = cur.right;}}// 比较 val 和记录下来的 parent.valif (val < parent.val) {parent.left = new TreeNode(val);} else {parent.right = new TreeNode(val);}}
2.3, 删除
删除之前要先查找到这个结点, 首先写出查找的代码
public void remove(int val) {if (root == null) {return;}TreeNode cur = root;TreeNode parent = null;while (cur != null) {parent = cur;if (val == cur.val) {// 找到了, 进行删除操作removeNode(parent, cur);System.out.println(val + "找到了,已删");return;} else if (val < cur.val) {cur = cur.left;} else {cur = cur.right;}}System.out.println(val +"没找到");}
❗️❗️❗️
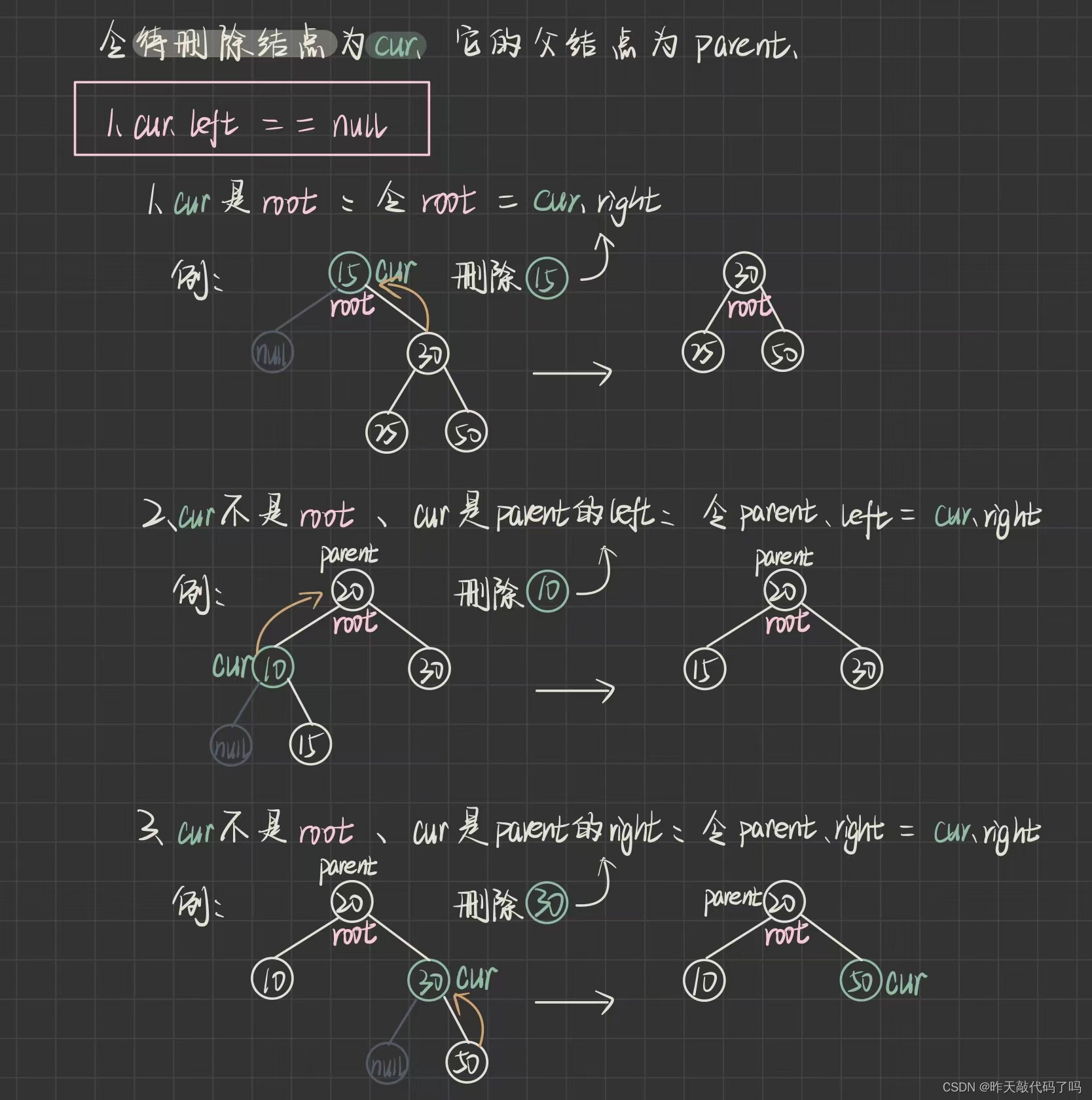
删除二叉搜索树中的数据比较复杂, 因为需要考虑删除某个数据后, 整棵树依然是二叉搜索树, 要判断待删除结点的左右孩子如何处置
分为三种情况讨论:
1️⃣cur.left == null 时又分为三种情况
2️⃣ cur.right == null 时又分为三种情况
3️⃣cur.left != null && cur.right != null 时需要"替换删除"
三种情况图解分析如下:
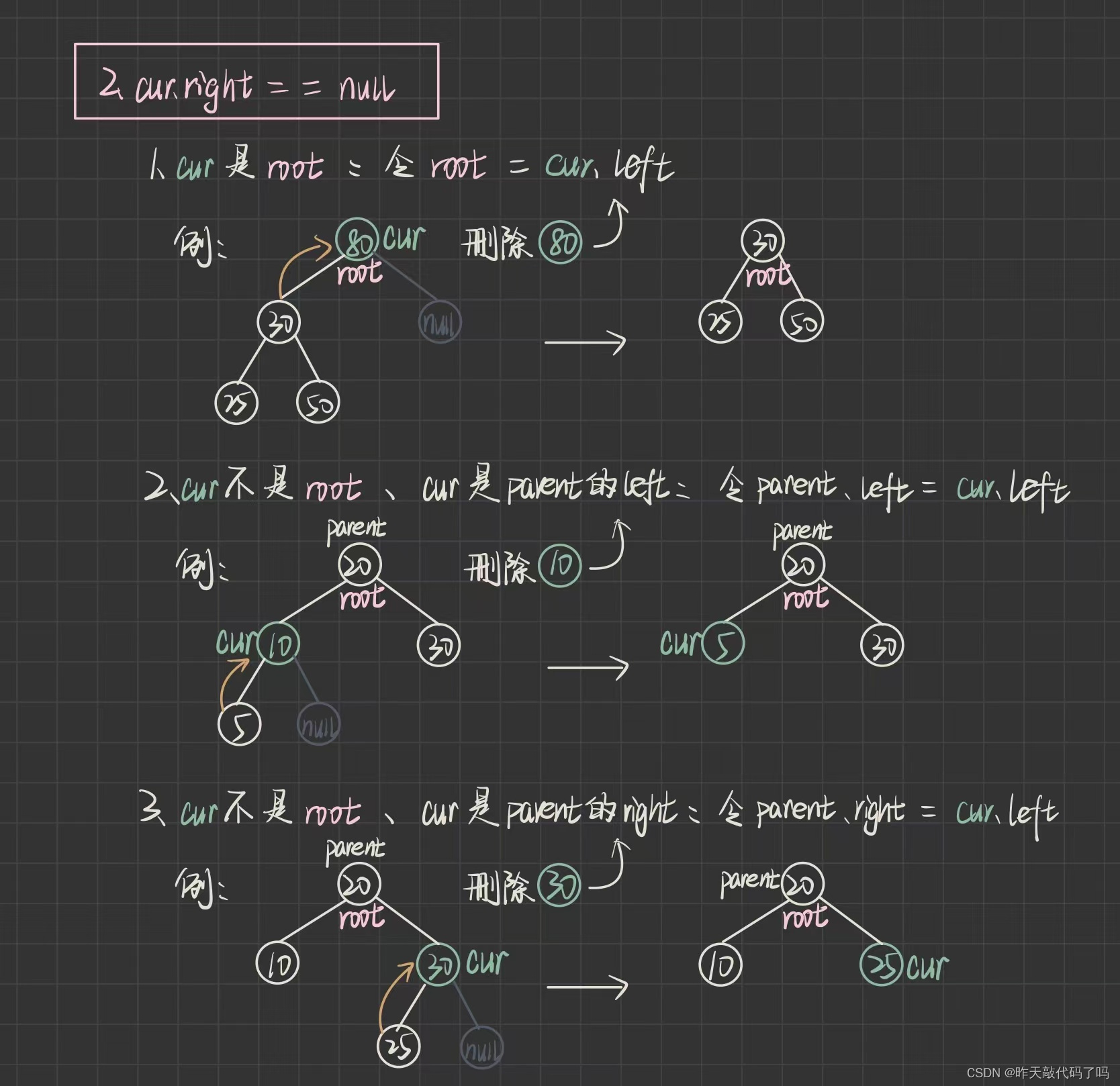
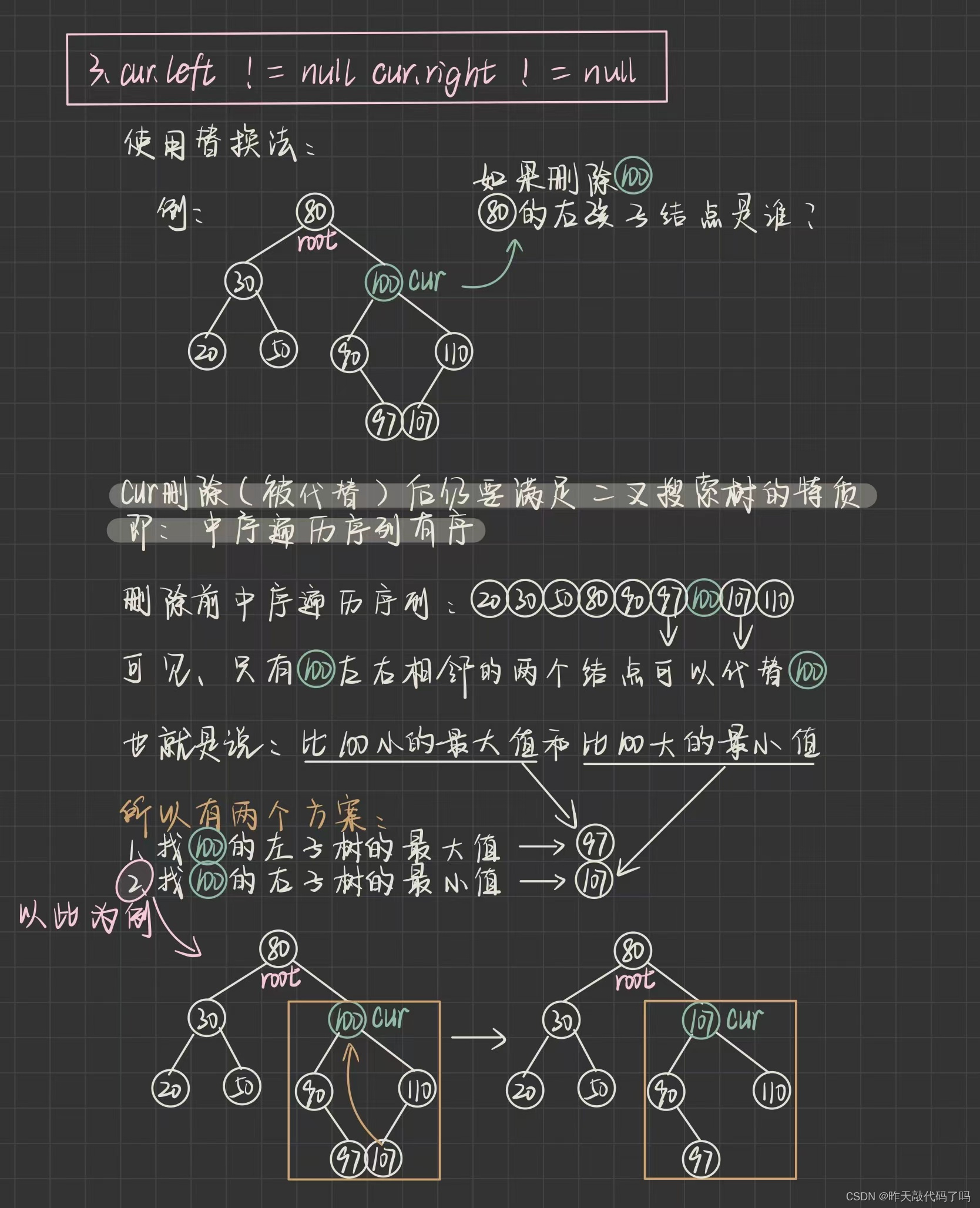
⚠️⚠️⚠️上图中最后一步实际上不是让 107 和 100 交换, 因为 100 还有左右子树的引用, 是让 107 这个结点的 val 值覆盖掉了 cur 这个结点的 val 值
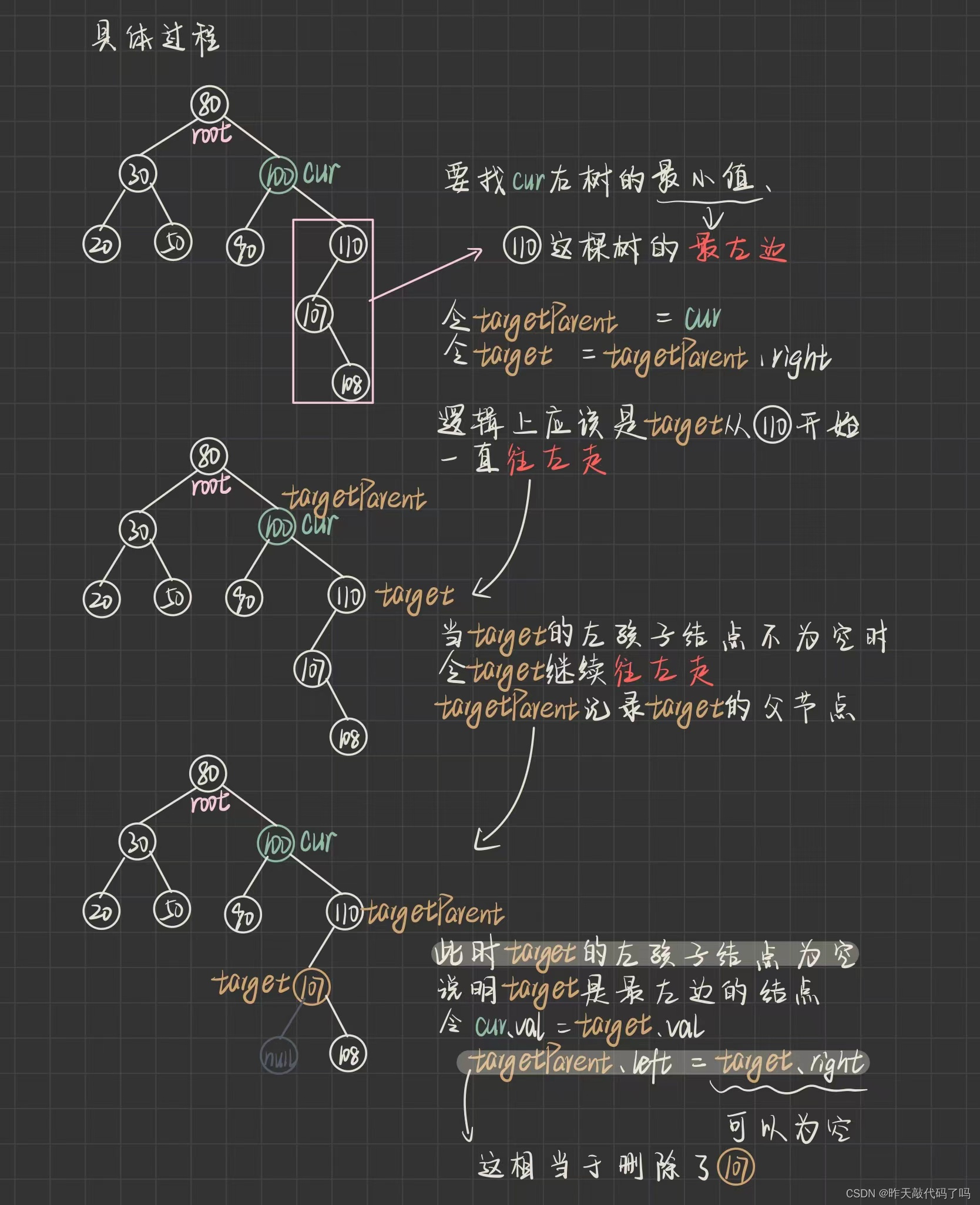
然后问题就转化成了如何删掉 107 这个结点, 具体如何找到 107 ,以及如何删掉 107 的过程如下:
代码实现:
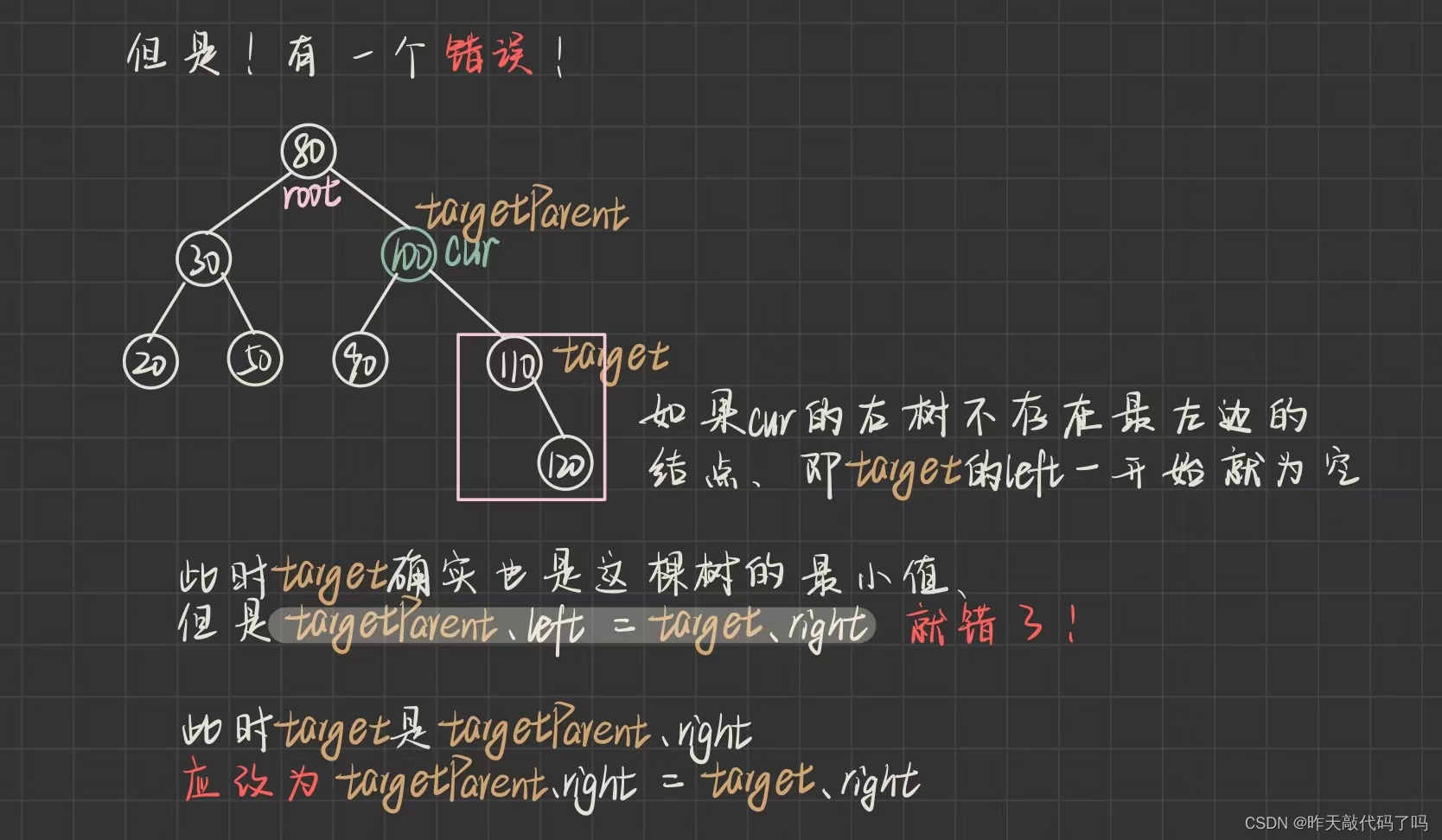
/*** 三种情况:* 1,左为空* 2,右为空* 3,左右都不空* @param root* @param cur*/private void removeNode(TreeNode root, TreeNode cur) {if (cur.left == null) {/*** 三种情况* 1,cur == root* 2,cur == root.left* 3,cur == root.right*/if (cur == root) {cur = cur.right;}else if(cur == root.left) {root.left = cur.right;}else{root.right = cur.right;}} else if (cur.right == null) {/*** 三种情况* 1,cur == root* 2,cur == root.left* 3,cur == root.right*/if(cur == root) {cur = cur.left;}else if(cur == root.left) {root.left = cur.left;}else {root.right = cur.left;}} else {TreeNode targetParent = cur;TreeNode target = cur.right;// 右树找最小值while (target.left != null) {targetParent = target;target = target.left;}cur.val = target.val;// 判断右树结点是否为为1if (target == targetParent.left) {targetParent.left = target.right;}if (target == targetParent.right) {targetParent.right = target.right;}}}
3、性能分析
二叉搜索树的搜索性能取决于结点之间的比较次数, 而这又取决于树的状态
👉最好情况下: 二叉搜索树是一棵近似平衡的完全二叉树状态, 时间复杂度达到 O(log2N)
👉最坏情况下: 二叉搜索树是一棵单分支的斜树, 时间复杂度达到 O(N)
插入和删除的性能同理
为了解决二叉搜索树最坏情况下是单分支结构时导致的性能性下降问题, 引出了VAL树, 它通过旋转子树处理, 使二叉搜索树接近于平衡, 以后详细介绍
二、模型
在学习二叉搜索树之前,接触过的搜索方式可能只有暴力遍历和二分查找,
暴力遍历在数据量大时效率很慢,而二分查找必须在使用前先保证数据集合有序,并且这两种方式都只适用于静态查找
现实生活中查找时很有可能同时伴随着插入和删除,这就是动态查找,本篇介绍的 Map 和 Set 就是适合于动态查找的集合容器
一般把搜索的数据称作关键字(Key), 和关键字对应的称作值(Value)
1️⃣纯Key模型: 只存储Key
一般可以看用于搜索某个关键字是否存在
2️⃣Key-Value模型: 存储 Key 和每个 Key 对应的Value
一般可以用于搜索某个关键字出现的次数(单词在句子中出现的次数等等)
👉Map 这种结构中存储的就是 Key-Value(称作键值对) , Set 这种结构中只存储 Key
关于 Map 和 Set 的具体使用方式, 哈希表之后再一起介绍
三、哈希表
顺序结构的顺序表, 堆, 链式结构的链表, 二叉搜索树等, 关键字和存储位置之间都没有对应关系, 所以在查找关键字时, 必须经过关键字之间的比较
顺序表, 链表查找的时间复杂度达到O(N), 二叉搜索树查找的时间复杂度达到O(log₂N) 或 O(N)
🚗🚗🚗
那有没有一种搜索方式能够不经过关键字之间的比较, 直接得到要搜索的关键字? 这样, 时间复杂度就能够达到O(1) ------ 正是哈希表, 恐怖如斯 ❗️
1、什么是哈希表
哈希表(散列表) 这种数据结构可以通过哈希(散列)函数, 使元素的存储位置和关键码(hashCode)之间有一一映射的关系, 在插入和查找数据时, 根据关键字的hashCode, 计算出存储位置
例如这样一组数据: 1, 7, 6, 4, 5, 9
如果令哈希函数为: f (key) = key % capacity , 则数据的存储方式如图所示:
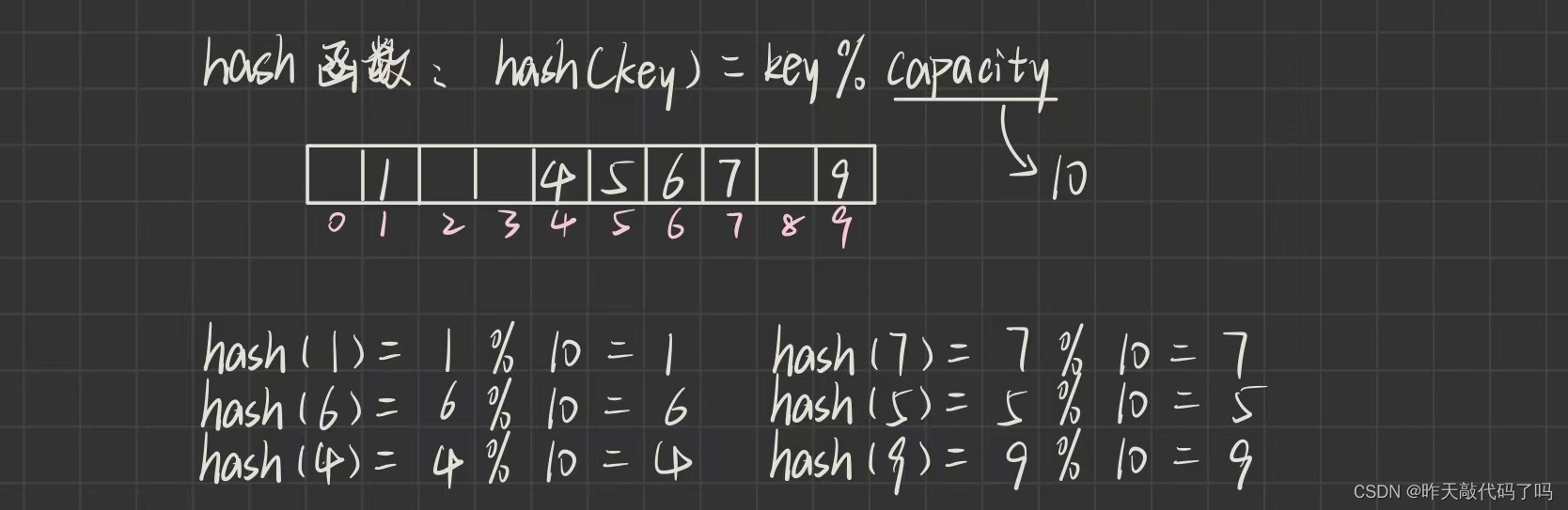
这样, 在搜索关键字时, 能够直接得到它的存储位置, 进行随机访问, 效率很高
但问题来了❗️❗️❗️ 依照如上哈希函数, 假如要再插入 14, 24, 34, 44 呢? 这些数据都会被存储到 4 下标这个位置, 可是 4 下标已经存储了关键字 4 了
这种情况叫做: 哈希冲突
1.1, 什么是哈希冲突
👉不同的关键字通过相同的哈希函数, 计算出来了相同的哈希地址, 这种现象就是哈希冲突(哈希碰撞)
如上述例子: 4, 14, 24, 34, 44 这几个
不同的关键字都通过相同的哈希函数: f (key) = key % capacity , 得到了相同的哈希地址: 4下标
👉把具有不同关键码但是哈希地址相同的数据称作" 同义词 ", 那么 4, 14, 24, 34, 44 就是同义词
1.2, 避免, 解决哈希冲突
要明确: 由于哈希表底层的数组容量往往小于实际存储的关键字数量, 这就导致一定会有多个关键字存储在同一个哈希地址上, 所以哈希冲突是无法消除的
但是, 还是有一些解决哈希冲突的方案的
一定要清楚!!
这里说的无法消除哈希冲突是指: 一定会有几个数据被分配到同一个哈希地址
而解决哈希冲突是指: 如果发生冲突, 不让他们同时存储在一个空间上
在解决哈希冲突之前, 首先要保证哈希函数的合理性, 有以下三点原则:
1️⃣哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有 m 个地址时,其值域必须在 0 到 m-1 之间
2️⃣哈希函数计算出来的地址能均匀分布在整个空间中
3️⃣哈希函数应该比较简单
哈希函数设计的越合理, 越精妙, 哈希冲突的概率越低, 但仍然无法消除
一般来说, 都是使用库里面的哈希函数, 不会让我们自己设计
下面介绍如何尽量避免和解决哈希冲突
1.2.1, 避免: 调节负载因子
负载因子(∝) : ∝ = 表中已有数据 / 表长度
假如规定负载因子为 0.75, 当哈希表长度为 10, 已经填入了 8 个数据时, 就超过了负载因子, 表中负载因子越大, 发生哈希冲突的概率就会越大, 此时需要调节负载因子, 让负载因子变小
由于无法控制表中要插入多少个数据(分子), 所以我们只能对数组扩容(分母)
⚠️⚠️⚠️注意:
填入第 8 个数据时, 发现负载因子已经大于0.75, 此时需要对数组扩容
如果哈希函数是: 关键字的关键码 % 数组长度, 那么当数组扩容之后, 数组长度改变,哈希函数改变, 哈希地址也要重新分配, 需要对表中的所有数据重新计算哈希地址, 重新分配存储空间
1.2.2, 解决1: 闭散列(了解)
由于闭散列的弊端较大, 所以一般不使用, 仅作了解
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的 “下一个” 空位置中去。那如何寻找下一个空位置呢
分为两种: 线性探测 和 二次探测
📌📌📌线性探测 : 冲突的数据, 依次往后面找空位置存放, 效果如图所示:
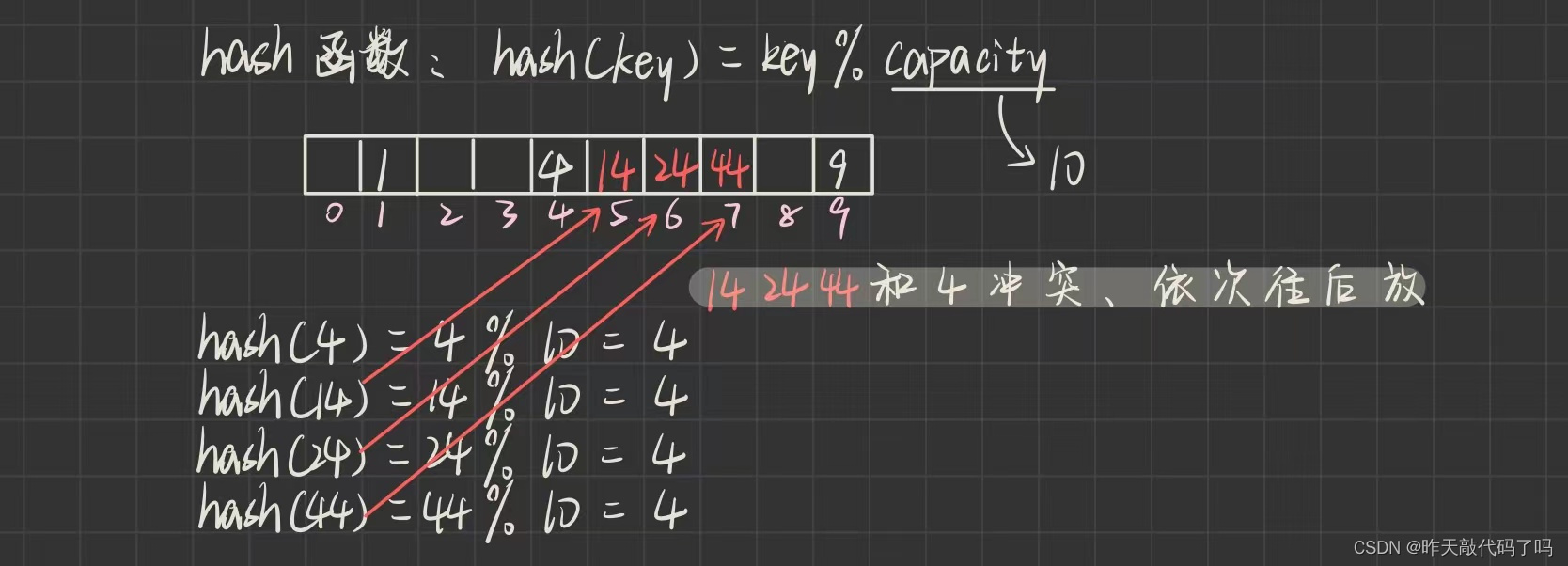
❌弊端:
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素会影响其他元素的搜索。比如删除元素4,如果直接删除掉,44查找起来可能会受影响。因此线性探测采用标记的伪删除法来删除一个元素。
📌📌📌二次探测 : 针对线性探测会把冲突的数据堆积到一起这个缺陷, 二次探测是通过某种函数, 重新计算了哈希地址, 使得冲突的数据能够相对分散一些 , 效果如图所示:
❌弊端
当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容。
综合来看, 闭散列的最大弊端就是空间利用率太低, 而第二种解决方案对空间利用率较高
1.2.3, 解决2: 开散列/哈希桶(重点)
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中
什么意思?🤷♂️
例如, HashMap 存储 <Key,Value> 模型的数据, Key表示数字, Value表示这个数字在某处出现的次数
插入 <1,0>, <4,3>, <7,2>, <14,5>, <44,8> , 哈希桶存储形式 如图所示:
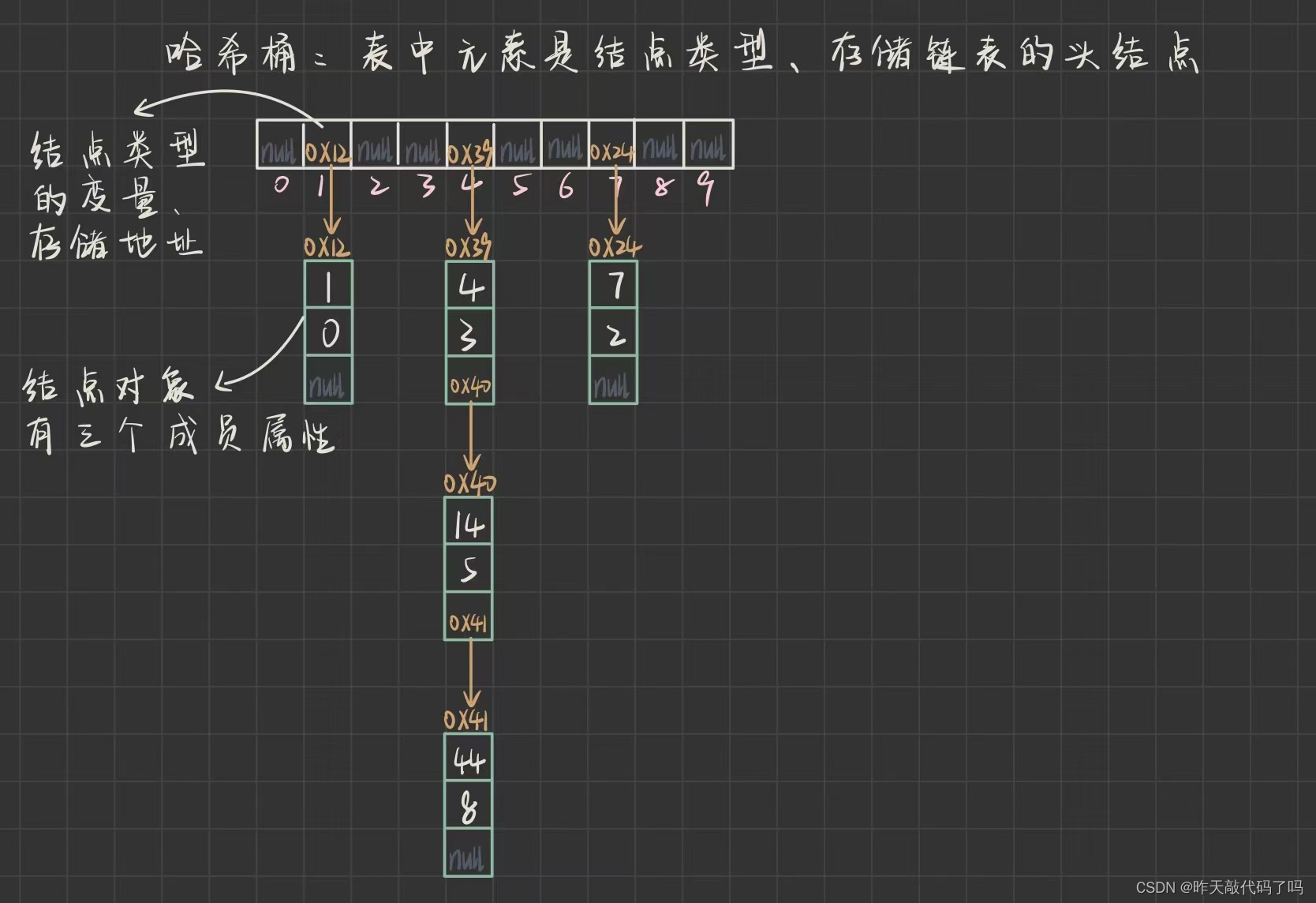
可以看到, 由于哈希表中每个下标存储的是一个链表的头结点, 因此可以 “同时” 存储多个哈希冲突的数据, 而不会像闭散列那种方案, 占用数组中其它空间, 所以开散列对表中空间利用率比较高
2、模拟实现哈希表
我们对哈希表(开散列/哈希桶的方式)进行模拟实现, 刚才了解过, 每个桶都是一个单链表(先不考虑红黑树), 链表是由结点(作为内部类)组织起来的
如果采用Key-Value 模型, 结点中就需要三个域:
两个值域: Key 和 Value, 以及一个指针域: next
先写出 HashBuck 的成员属性
public class HashBuck {static class Node{public int key;public int val;public Node next;public Node(int key,int val) {this.key = key;this.val = val;}}public Node[] array;public int uesdSize;public static final double LOAD_FACTOR = 0.75;// 负载因子public HashBuck(int capacity){array = new Node[10];// 没有初始化数组,里面每一个结点默认是null}
Java集合里的哈希桶中设定负载因子就是0.75
为了方便理解 + 代码易懂, 暂时不使用泛型以及封装
主要模拟实现插入Key-Value键值对和获取Key的Value值这两种操作
2.1, put — 插入 Key-Value 键值对
插入是对在哈希桶(链表)中进行插入删除操作, jdk1.8 之前是头插, 之后修改为尾插, 头插难度稍大, 在这里以头插的方式展现
设定哈希函数为: index(哈希地址) = key % array.length;
public void put(int key,int val) {int index = key % array.length;Node cur = array[index];// 遍历这个哈希值对应的链表中的结点,如果有相同的就替换掉// 如果没有就头插while(cur != null){if (cur.key == key) {cur.val = val;return;}cur = cur.next;uesdSize++;}Node node = new Node(key, val);// newArray[newIndex] 中存储的是链表的头结点node.next = array[index];// 存储新的头结点array[index] = node;uesdSize++;// 判断此时是否已经超过LOAD_FACTOR负载因子的值if (uesdSize * 1.0 / array.length > LOAD_FACTOR) {// 扩容grow();}}
⚠️⚠️⚠️每次插入完后, 都需要计算负载因子是否超过0.75, 如果超过需要对数组扩容
2.1.1, resize — 扩容, 调节负载因子
private void grow() {Node[] newArray = Arrays.copyOf(array, array.length * 2);for (Node node : array) {// 重新分布每一个结点的新的哈希地址Node cur = node;while (cur != null) {Node curNext = cur.next;int newIndex = cur.key % newArray.length;// newArray[newIndex] 中存储的是链表的头结点cur.next = newArray[newIndex];newArray[newIndex] = cur;cur = curNext;}}array = newArray;}
2.2, get —获取 Key 的 Value 值
public int get(int key) {int index = key % array.length;Node cur = array[index];while (cur != null) {if (cur.key == key) {return cur.val;}cur = cur.next;}// 也可以抛异常throw new TheKeyDoesNotExistException("没有这个key值");}
3、性能分析
尽管哈希表一定发生会冲突, 但Java集合中采用 哈希桶 这种方式解决冲突, 发生冲突的数据以链表的方式存储, 加之 调节负载因子 , 所以链表的长度 = 冲突数据的个数, 会远小于表中数据, 所以链表的长度是一个常数
因此通常意义下,我们认为哈希表的 插入 / 删除 / 查找 时间复杂度是O(1)
四、Java 提供的 TreeMap 和 HashMap
Map是一个接口类,该类没有继承自Collection,该类中存储的是<K,V>结构的键值对,并且K一定是唯一的,不能重复, TreeMap 是用红黑树实现的, HashMap 是用哈希表实现的
实例化方式:
public static void main(String[] args) {// 第一个参数代表Key, 第二个参数代表ValueMap<Character, Integer> treeMap = new TreeMap<>();Map<Character, Integer> hashMap = new HashMap<>();}
1, Map 常用方法
下面介绍集合中 TreeMap 和 HashMap 常用的方法都是一样的, 只是底层数据结构不一样, 以 TreeMap 为例
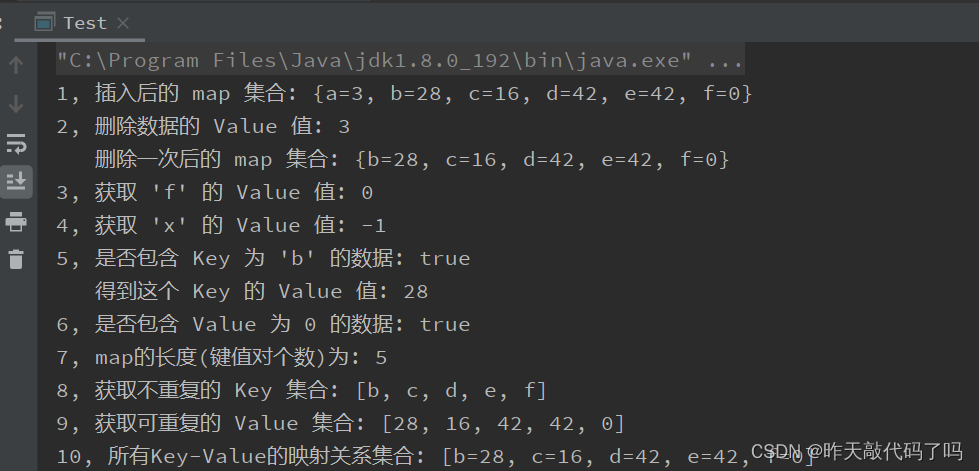
public static void main89(String[] args) {Map<Character, Integer> treeMap = new TreeMap<>();// 1,插入数据treeMap.put('a',3); // 字符'a'代表Key, 整型3代表ValuetreeMap.put('d',42);treeMap.put('c',16);treeMap.put('e',42);treeMap.put('b',28);treeMap.put('f',99);treeMap.put('f',0);System.out.println("1, 插入后的 map 集合: " + treeMap);// 2,删除数据int removeValue = treeMap.remove('a');System.out.println("2, 删除数据的 Value 值: " + removeValue);System.out.println(" 删除一次后的 map 集合: " + treeMap);// 3,获取Key对应的Value值int getValue = treeMap.get('f');System.out.println("3, 获取 'f' 的 Value 值: " + getValue);// 4,如果Key不存在, 获取默认Value值int getDefaultValue = treeMap.getOrDefault('x',-1);// 'x' 不存在, 设置Value值默认为-1System.out.println("4, 获取 'x' 的 Value 值: " + getDefaultValue);// 5,判断是否包含Keyboolean containsKey = treeMap.containsKey('b');System.out.println("5, 是否包含 Key 为 'b' 的数据: " + containsKey);System.out.println(" 得到这个 Key 的 Value 值: " + treeMap.get('b'));// 6,判断是否包含Valueboolean containsValue = treeMap.containsValue(0);System.out.println("6, 是否包含 Value 为 0 的数据: " + containsValue);// 7,获取map的长度(键值对个数)int size = treeMap.size();System.out.println("7, map的长度(键值对个数)为: " + size);// 8,获取不重复的Key集合Set<Character> retSet = treeMap.keySet();System.out.println("8, 获取不重复的 Key 集合: " + retSet);// 9,获取可重复的Value集合Collection<Integer> retValue = treeMap.values();System.out.println("9, 获取可重复的 Value 集合: " + retValue);// 10,获取所有Key-Value的映射关系集合Set<Map.Entry<Character, Integer>> enteySet = treeMap.entrySet();System.out.println("10, 所有Key-Value的映射关系集合: " + enteySet);}
输出结果:
1.1, 关于 Entry 的说明:
第十条中,Map.Entry<Character, Integer> 是啥?
Entry<K, V>是 Map 内部实现的用来存放 <key, value> 键值对映射关系的内部接口, 所以通过 " . " 点号可以访问这个内部接口
Set 中的数据是 纯Key 模型, treeMap.entrySet() 这个方法就是把所有的 Key-Value 键值对的映射关系存放在 Set 中, Set 的对象中每一个数据的类型是 Entry
如图:
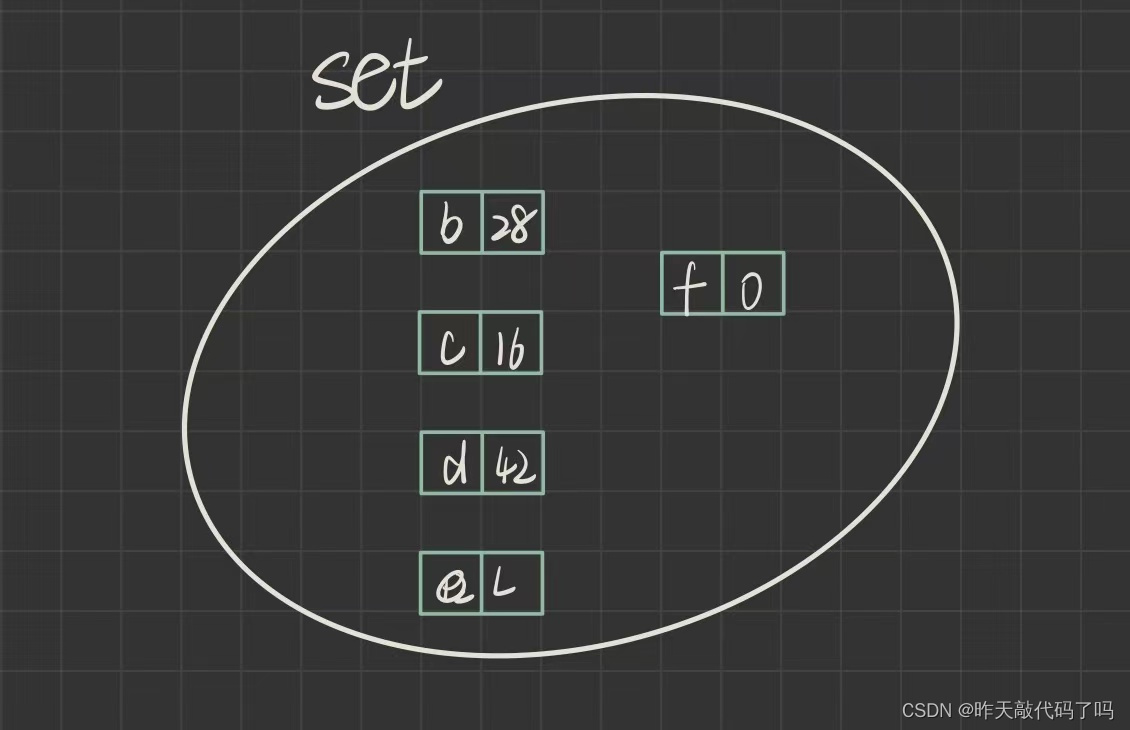
对这个 set 使用 fro-each 遍历, 即可得到其中的每一个 entry
for(Map.Entry<Character, Integer> entry : enteySet) {}
1.2, Entry 的常用方法:
Entry 这个内部接口中主要提供了 <key, value> 的获取,value 的设置以及 Key 的比较方式。
使用方式如下:
for(Map.Entry<Character, Integer> entry : enteySet) {// 获取entry (键值对)中的Keychar keyRet = entry.getKey();// 获取entry (键值对)中的valueint valueRet = entry.getValue();System.out.println("key = " + keyRet + " , value = " + valueRet);if(keyRet == 'b') {// 修改value值int updateRet = entry.setValue(-valueRet);System.out.println("把 key 为 'b' 的键值对的 value 值改为负数: " + updateRet);}}
Value值可以修改, 但是Key值是不可以, 不支持修改的
2, Map 注意事项
1️⃣Map 是一个接口,不能直接实例化对象,如果要实例化对象只能实例化其实现类: TreeMap 或者 HashMap
2️⃣Map 中存放键值对的 Key 是唯一的(不可重复),value 是可以重复的
在上述代码示例中, 插入了< ’ f ’ , 99> , 又插入了< ’ f ’ , 0>
第二次插入时已经存在一个 Key 值为 ’ f ’ , 由于 Key 不可重复, 所以 < ’ f ’ , 0> 会直接覆盖掉 < ’ f ’ , 99>
因此, 输出的第三行显示: ’ f ’ 对应的 Value 值为 0
3️⃣在 TreeMap 中插入键值对时,key 不能为空,否则就会抛 NullPointerException 异常,value 可以为空。但是 HashMap 的 key 和 value 都可以为空
因为 TreeMap 是用红黑树实现的, 上面介绍二叉搜索树中说过, 树结构的增删查改需要经过关键字之间的比较, 如果关键字为 null 就不可以比较了, 所以会抛异常
4️⃣Map 中的 Key 可以全部分离出来,存储到 Set 中来进行访问(因为 Key 不能重复)
因为 Set 中的数据不可以重复, 可以达到去重的目的, 下面会介绍到
5️⃣Map 中的 value 可以全部分离出来,存储在 Collection 的任何一个子集合中( value 可能有重复)
6️⃣Map 中键值对的 Key 不能直接修改,value 可以修改,如果要修改 key,只能先将该 key 删除掉,然后再来进行重新插入
3, TreeMap 和 HashMap 的区别
如图
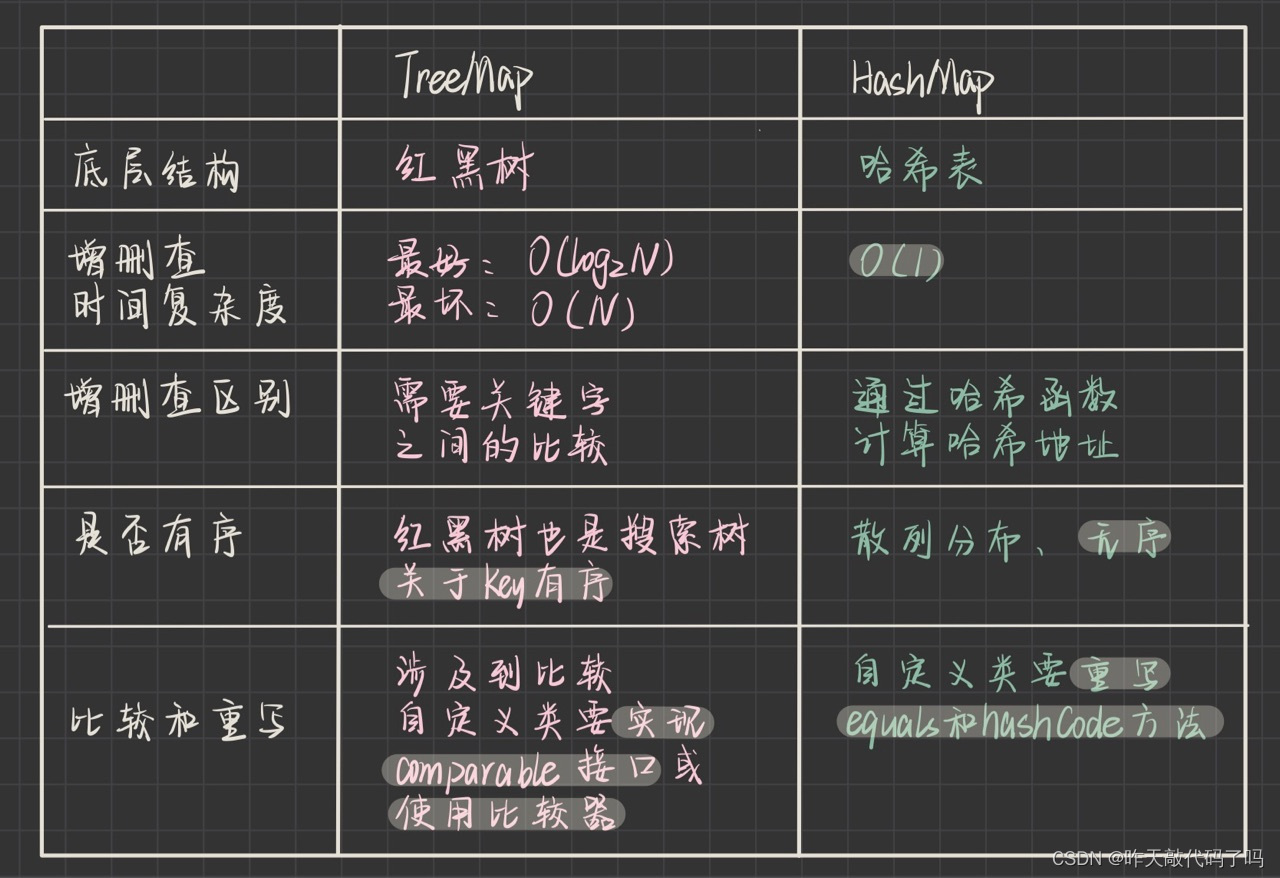
那什么时候使用 TreeMap,什么时候使用 HashMap 呢
如果要求Key在集合中保持有序,就使用 TreeMap,如果不要求Key有序,或追求性能高,时间快,则使用HashMap
五、Java 提供的 TreeSet 和 HashSet
Set 与 Map 主要的不同有两点:1️⃣Set 是继承自 Collection 的接口类,2️⃣Set 中只存储了 Key
Set 中 K一定是唯一的,不能重复, 所以 Set 有去重的功能, TreeSet 是用红黑树实现的, HashSet 是用哈希表实现的
实例化方式:
public static void main(String[] args) {Set<Integer> treeSet = new TreeSet<>();Set<Integer> hashSet = new HashSet<>();}
1, Set 常用方法
下面介绍集合中 TreeSet和 HashSet 常用的方法都是一样的, 只是底层数据结构不一样, 这次以 HashSet 为例
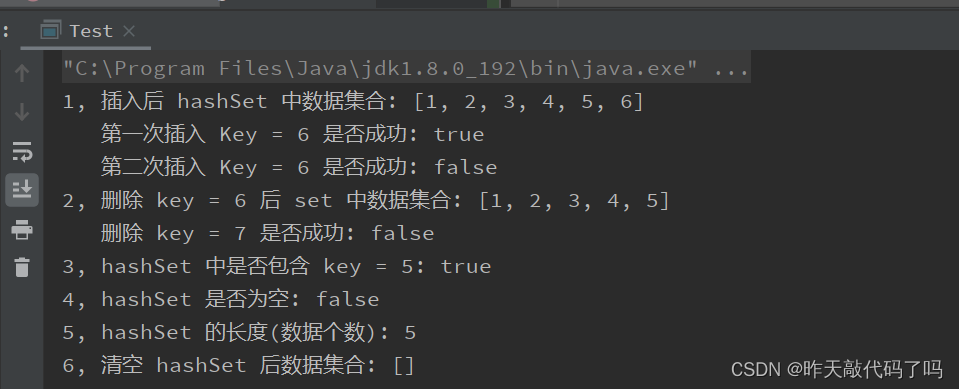
public static void main(String[] args) {Set<Integer> hashSet = new HashSet<>();// 1,插入数据hashSet.add(1);hashSet.add(2);hashSet.add(3);hashSet.add(4);hashSet.add(5);boolean firstAdd = hashSet.add(6);boolean secondAdd = hashSet.add(6);System.out.println("1, 插入后 hashSet 中数据集合: " + hashSet);System.out.println(" 第一次插入 Key = 6 是否成功: " + firstAdd);System.out.println(" 第二次插入 Key = 6 是否成功: " + secondAdd);// 重复的Key不能再插入// 2,删除数据hashSet.remove(6);boolean removeRet = hashSet.remove(7);// 不存在的数据不能删除System.out.println("2, 删除 key = 6 后 set 中数据集合: " + hashSet);System.out.println(" 删除 key = 7 是否成功: " + removeRet);// 3,判断是否包含某个keyboolean containsRet = hashSet.contains(5);System.out.println("3, hashSet 中是否包含 key = 5: " + containsRet);// 4,判断是否为空boolean emptyRet = hashSet.isEmpty();System.out.println("4, hashSet 是否为空: " + emptyRet);// 5,获取hashSet的长度(数据个数)int size = hashSet.size();System.out.println("5, hashSet 的长度(数据个数): " + size);// 6,清空hashSethashSet.clear();System.out.println("6, 清空 hashSet 后数据集合: " + hashSet);}
输出结果:
2, Set 注意事项
1️⃣Set 是继承自 Collection 的一个接口类
2️⃣Set 中只存储了 key,并且要求 key 一定要唯一
Set 可以达到去重的目的
3️⃣TreeSet 的底层是使用 Map 来实现的,其使用 key 与 Object 的一个默认对象作为键值对插入到 Map 中的
4️⃣Set 最大的功能就是对集合中的元素进行去重
5️⃣实现 Set 接口的常用类有 TreeSet 和 HashSet ,还有一个 LinkedHashSet,LinkedHashSet 是在HashSet的基础上维护了一个双向链表来记录元素的插入次序
6️⃣Set 中的 Key 不能修改,如果要修改,先将原来的删除掉,然后再重新插入
7️⃣TreeSet 中不能插入 null 的 key,HashSe t可以
因为 HashSe 底层是由哈希表实现的, 哈希表的操作不需要关键字之间的比较
3, TreeSet和HashSet的区别
TreeMap 和 HashMap 的区别就是 TreeSet 和 HashSet 的区别
如图:

什么时候使用 TreeSet ,什么时候使用 HashSet ? 参考 TreeMap 和 HashMap
总结
以上就是本篇的所有内容了, 本篇主要介绍了
1️⃣Java 集合中 Map 和 Set 接口底层的数据结构: 二叉搜索树 和 哈希表
2️⃣介绍了 Map 和 Set 中存储的两种数据模型
3️⃣介绍了 Map 和 Set 的常用方法的使用方式以及一些细节要点
如果本篇对你有帮助,请点赞收藏支持一下,小手一抖就是对作者莫大的鼓励啦😋😋😋~
上山总比下山辛苦
下篇文章见
相关文章:

Java【二叉搜索树和哈希表】详细图解 / 模拟实现 + 【Map和Set】常用方法介绍
文章目录前言一、二叉搜索树1、什么是二叉搜索树2、模拟实现二叉搜索树2.1, 查找2.2, 插入2.3, 删除3、性能分析二、模型三、哈希表1、什么是哈希表1.1, 什么是哈希冲突1.2, 避免, 解决哈希冲突1.2.1, 避免: 调节负载因子1.2.2, 解决1: 闭散列(了解)1.2.3, 解决2: 开散列/哈希桶…...

如何用 C 语言实现文本特征提取?
文本特征提取是一种将文本转换为数字或向量表示的技术,它是自然语言处理中的重要步骤。以下是一些用 C 语言实现文本特征提取的基本方法:基于词袋模型的特征提取词袋模型是一种将文本表示为单词频率的方法,可以通过以下步骤实现:将…...

ESD静电保护器件分类简介及场景应用
文章目录 1. ESD介绍1.1 ESD简介1.2 ESD产生原理1.3 ESD危害2. 器件级ESD模型2.1 人体模型(HBM)2.2 机器模型(MM)2.3 带电器件模型(CDM)3. 系统级ESD模型3.1 介绍3.2 防护器件分类简介3.2.1 TVS二极管3.2.2 MLCC陶瓷电容3.2.3 ESD抑制管3.2.4 MOV压敏电阻3.2.5 比较4. ES…...

硅谷银行倒闭的几点启示
摘要:本文从公开资料分析一下硅谷银行对信息科技行业的我们有一些什么启示。硅谷银行“拔网线”了,想创业的您,该注意了。1.硅谷银行是谁我们从其官网的说明来看看。The financial partner of the innovation economy.(翻译成中文…...

【AWS入门】IAM基本应用-2023/3/4
目录IAM概述根用户和IAM用户参考IAM概述 IAM(Identity Access Management)是身份和访问管理服务,要访问AWS服务和资源,就要使用IAM进行身份验证和授权。当我们通过控制台,CLI,或API访问AWS服务时,都需要通…...

RabbitMQ系列(1)--RabbitMQ简介
1、RabbitMQ概念RabbitMQ是一个消息中间件,不对消息进行处理,只对消息做接收、存储和转发。2、RabbitMQ四大核心概念(1)生产者产生数据发送信息的程序(2)交换机交换机是RabbitMQ中一个非常重要的部件,接收来着生产者的消息并把消息推送到队列…...
aws dynamodb 使用awsapi和PartiQL掌握dynamodb的CRUD操作
总结一下 dynamodb通常和java等后端sdk结合使用使用的形式可以是api或partiql语法调用dynamodb的用法不难,更重要的是维护成本,所需的服务集成,技术选型等和大数据结合场景下有独特优势 之后可能再看看java sdk中DynamoDBMapper的写法&…...
【C++学习】类和对象(上)
前言: 由于之前电脑“嗝屁”了,导致这之前一直没有更新博客,今天才拿到电脑,在这里说声抱歉。接下来就进入今天的学习,在之前我们已经对【C】进行了初步的认识,有了之前的知识铺垫,今天我们将来…...

一文带你深入理解【Java基础】· Java反射机制(下)
写在前面 Hello大家好, 我是【麟-小白】,一位软件工程专业的学生,喜好计算机知识。希望大家能够一起学习进步呀!本人是一名在读大学生,专业水平有限,如发现错误或不足之处,请多多指正࿰…...
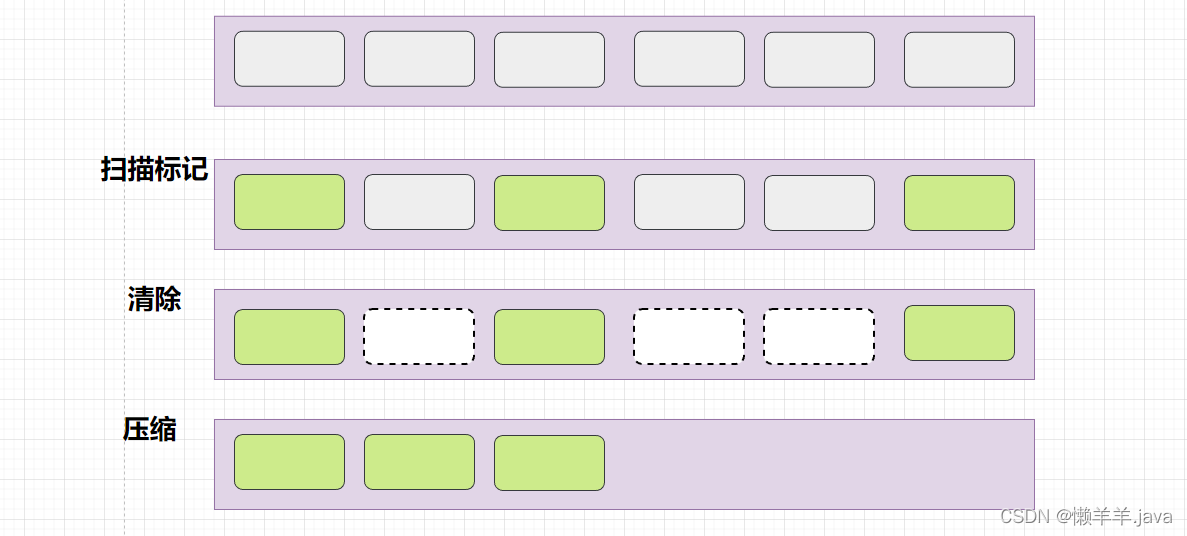
JVM的几种GC
GC JVM在进行GC时,并不是对这三个区域统一回收。大部分时候,回收都是新生代~ 新生代GC(minor GC): 指发生在新生代的垃圾回收动作,因为Java对象大多都具备朝生夕灭的特点,所以minor GC发生得非…...
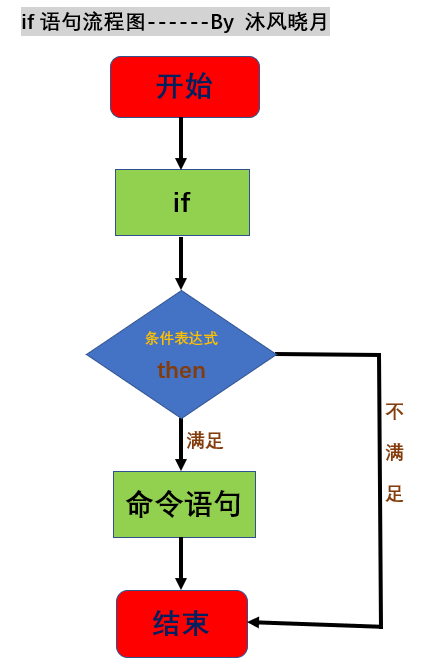
掌握Shell脚本的if语句,让你的代码更加精准和高效
前言 大家好,我是沐风晓月,本文首发于csdn, 作者: 我是沐风晓月。 文章收录于 我是沐风晓月csdn专栏 【系统架构实战】专栏中的【shell脚本入门到精通】专栏。 本专栏从零基础带你层层深入,学会shell脚本,不是梦。 &…...

音质好的蓝牙耳机有哪些?音质最好的蓝牙耳机排行
说起当代人外出必备是数码产品,蓝牙耳机肯定存在。不管是听歌还是追剧,蓝牙耳机在音质上的表现也是越来越好了。下面,我来给大家推荐几款音质好的蓝牙耳机,一起来看看吧。 一、南卡小音舱蓝牙耳机 参考价:259 蓝牙版…...

一次Android App NDK崩溃问题的分析及解决
文章目录小结NDK崩溃的问题通过logcat查看崩溃日志提取tombstone的记录通过ndk-stack来输出日志取得的日志分析并解决分析使用add2line定位具体报错的行数解决参考小结 最近碰一次Android App NDK崩溃的问题,这个NE(Native Exception)是从ND…...
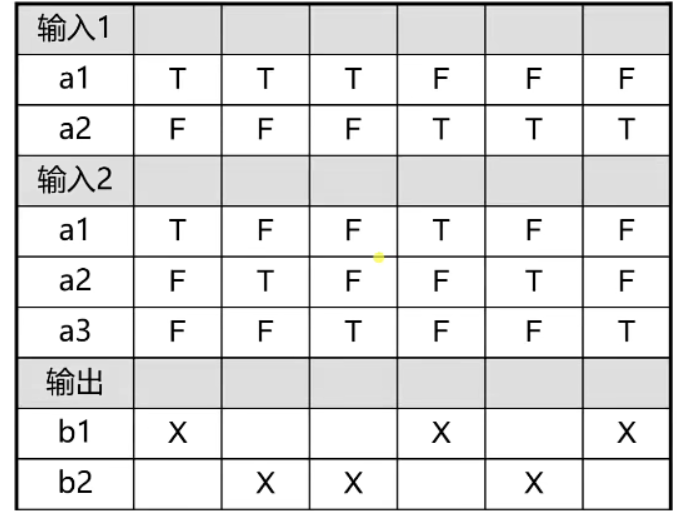
因果图判定表法
因果图&判定表法 在了解了等价类和边界值比较适宜搭档的测试用例方法之后 接下来我们来了解另外一队就是因果图和判定表 因果图会产生判定表法 因果图法 等价类划分法和边界值分析方法都是着重考虑输入条件而不考虑输入条件的各种组合、输入条件之间的相互制约关系。例…...

Oracle 数据库相关信息清单列表
Oracle 数据库相关信息清单列表 一、设置Oracle安装目录 Oracle基目录(ORACLE_BASE):D:\databases\oracle\oracle_11g\app\Administrator 软件位置(ORACLE_HOME):D:\databases\oracle\oracle_11g\app\Administrator\product\11.2.0\dbhome_1 数据库文件位置:D:\databa…...

射频资料搜集--推荐几个网站和链接
https://picture.iczhiku.com/resource/eetop/wHKYFQlDTRRShCcc.pdfhttps://picture.iczhiku.com/resource/eetop/wHKYFQlDTRRShCcc.pdfVCO pulling的资料 模拟滤波器与电路设计手册 - 射频微波仿真 - RF技术社区 Practical RF Amplifier Design Using the Available Gain Pr…...

B1048 数字加密
decription 本题要求实现一种数字加密方法。首先固定一个加密用正整数 A,对任一正整数 B,将其每 1 位数字与 A 的对应位置上的数字进行以下运算:对奇数位,对应位的数字相加后对 13 取余——这里用 J 代表 10、Q 代表 11、K 代表 …...

Qt使用FFmpeg播放视频
一、使用场景 因为项目中需要加载MP4播放开机视频,而我们的设备所使用的架构为arm架构,其中缺乏一些多媒体库。安装这些插件库比较麻烦,所以最终决定使用FFmpeg播放视频。 二、下载编译ffmpeg库 2.1 下载源码 源码下载路径:http…...
Win32 ListBox控件
Win32 ListBox控件 创建ListBox控件 创建窗口函数 HWND CrateWindowEx(DWORD dwExStyle , // 窗口的扩展风格,基本没用LPCTSTR lpClassName, // 已经注册的窗口类名称LPCTSTR lpWindowName, // 窗口标题栏的名字DWORD dwStyle, // 窗口的基本风格int x, // 左上角水平坐标int …...
最大值池化与均值池化比较分析
1 问题在深度学习的卷积网络过程中,神经网络有卷积层,池化层,全连接层。而池化层有最大值池化和均值池化两种情况,而我们组就在思考,最大值池化和均值池化有什么区别呢?两者的模型准确率是否有所不同&#…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
