算法设计与分析--考试真题
- 分布式算法试题汇总
- 选择题
- 简答题
- 算法题
- 2013级试题
- 2019级试题
- 2021年秋
- 考卷
根据考试范围找相应题目做。
分布式算法试题汇总
选择题





-
下述说法错误的是___
A 异步系统中的消息延迟是不确定的
B 分布式算法的消息复杂性是指在所有合法的执行上发送消息总数的最大值
C 在一个异步算法中,如果不存在错误,则算法的执行只取决于初始配置
D 分布式系统终止是指系统中所有结点处于终止状态,且没有消息在传输 -
已知有三个阻碍分布式了解全局状态,与全局状态无关的是 ()
A. 非及时的通信
B. 相关性影响
C. 中断
D. 算法的正确性
在分布式系统中,有三个主要的阻碍了解全局状态的因素,分别是:
- 非及时的通信:由于网络延迟,消息的传递可能不是按照发送的顺序到达接收方,导致事件的顺序不一致,从而影响全局状态的判断。
- 相关性影响:由于分布式系统中的组件之间存在依赖关系,一个组件的状态可能会影响另一个组件的状态,从而影响全局状态的判断。
- 中断:由于分布式系统中的组件可能会发生故障或恢复,导致系统的可用性和一致性受到影响,从而影响全局状态的判断。
因此,与全局状态无关的是算法的正确性。算法的正确性是指算法能够按照预期的功能和性能执行,不受外部因素的干扰。算法的正确性是分布式系统设计和实现的基础,而不是了解全局状态的障碍。
-
设正整数d1,d2,…,dn是n个结点的标识符集合,x = min(d1,d2,…,dn),y =max(d1,d2,…,dn),则同步环上非均匀的leader选举算法的时间复杂性是
A. O(n)
B. O(xn)
C. (yn)
D. O(nlogn) -
在异步环上,一个O(n^2)的leader选举算法按顺时针单向发送消息,假设只有最大的标识符节点可以当选为leader,则当环上标识符次序为__时该算法发送的消息数量最多。
A. 0,1, … , n-1 随机
B. 逆时针 n-1,n-2,…,0
C. 顺时序 0,1,…, n-1
D. 顺时针 n-1,n-2,…,0
简答题
- 已知事件 e1,e2,e3 和 e4 的向量时戳分别为(2,3,0,0),(1,2,0,0),(0,0,1,1),(3,6,4,2),请找出所有因果关系的事件对。
(1,2,0,0)<v (2,3,0,0),e2 在因果序上先于 e1
(2,3,0,0)<v (3,6,4,2),e1 在因果序上先于 e4
(1,2,0,0)<v (3,6,4,2),e2 在因果序上先于 e4
(0,0,1,1)<v (3,6,4,2),e3 在因果序上先于 e4
如果事件e1在事件e2之前发生,或者事件e1导致事件e2发生,那么事件e1因果先于事件e2,记为e1 -> e2。向量时戳的一个重要性质是,如果 e 1 < v e 2 e1 <_v e2 e1<ve2,那么e1的向量时戳的每个元素都小于或等于e2的向量时戳的对应元素。
- 分布式算法中,bit复杂性和消息链复杂性分别属于通信复杂性和时间复杂性中的哪一种?
bit 复杂性属于通信复杂性,消息链复杂性属于时间复杂性;若在一个分布式算法中每个 msg信息的 bit 数目相同,则 msg 的个数就等于 bit 的总数除以一个 msg 的 bit 数目,则 bit 复杂性可以等价为 msg 复杂性;消息链复杂性是最长消息链的长度,在同步系统中它就是最大轮数,异步系统中假定任何执行的 msg 延迟至多是一个单位时间,它就是计算直到终止时间的最大运行时间,在同,异步系统中皆为时间复杂性。
- 通信复杂性可以进一步分为两种:bit复杂性和消息复杂性。bit复杂性是指算法在执行过程中所传输的比特数,它反映了算法的通信量。消息复杂性是指算法在执行过程中所传输的消息数,它反映了算法的通信次数。
- 时间复杂性也可以进一步分为两种:同步时间复杂性和异步时间复杂性。同步时间复杂性是指算法在同步模型下的执行时间,它反映了算法的同步性能。异步时间复杂性是指算法在异步模型下的执行时间,它反映了算法的异步性能。
因此,bit复杂性属于通信复杂性中的一种,而消息链复杂性属于时间复杂性中的一种。消息链复杂性是指算法在异步模型下的最长消息链的长度,它反映了算法的最坏情况下的延迟。
消息复杂性和消息链复杂性的区别:
消息复杂性和消息链复杂性是两种不同的时间复杂性的指标,它们分别反映了算法在通信次数和延迟方面的性能。- 消息复杂性是指算法在执行过程中所传输的消息数,它反映了算法的通信次数。消息复杂性越小,说明算法的通信开销越低。
- 消息链复杂性是指算法在异步模型下的最长消息链的长度,它反映了算法的延迟。消息链复杂性越小,说明算法的响应时间越快。
- 构造一个 16 节点的环,使其高度对称,并给出所有序等价的连续片段。
0 0000 0000 0
1 0001 1000 8
2 0010 0100 4
3 0011 1100 12
4 0100 0010 2
5 0101 1010 10
6 0110 0110 6
7 0111 1110 14
8 1000 0001 1
9 1001 1001 9
10 1010 0101 5
11 1011 1101 13
12 1100 0011 3
13 1101 1011 11
14 1110 0111 7
15 1111 1111 15
长度为 1 的有序等价的连续片段:
(0),(8), (4), (12), (2), (10), (6), (14), (1), (9), (5), (13), (3), (11), (7), (15)
长度为 2 的有序等价的连续片段:
(0, 8),(4, 12),(2, 10),(6, 14),(1, 9), (5, 13), (3, 11), (7, 15);
(8, 4), (12, 2), (10, 6), (14, 1), (9, 5), (13, 3), (11, 0)
长度为 4 的有序等价的连续片段:
0, 8, 4, 12 || 2, 10, 6, 14 || 1, 9, 5, 13 || 3, 11, 7, 15;
15 0, 8, 4 || 12, 2, 10, 6 || 14, 1, 9, 5 || 13, 3, 11, 7;
7, 15 0, 8, || 4, 12, 2, 10, || 6, 14 1, 9, || 5, 13 3, 11;
11, 7, 15 0, || 8, 4, 12, 2, || 10, 6, 14, 1, || 9, 5, 13 3;
长度为 8 的有序等价的连续片段:
0, 8, 4, 12 2, 10, 6, 14 || 1, 9, 5, 13 || 3, 11, 7, 15;
15 0, 8, 4 12, 2, 10, 6 || 14, 1, 9, 5 , 13, 3, 11, 7;
7, 15 0, 8, 4, 12, 2, 10, || 6, 14 1, 9, 5, 13 3, 11;
11, 7, 15 0, 8, 4, 12, 2, || 10, 6, 14, 1, 9, 5, 13, 3;
3, 11, 7, 15 0, 8, 4, 12, || 2 10, 6, 14, 1, 9, 5, 13 ;
13, 3 11, 7, 15 0, 8, 4, || 12, 2 10, 6, 14, 1, 9, 5;
5, 13, 3 11, 7, 15 0, 8, || 4 12, 2 10, 6, 14, 1, 9 ;
9, 5, 13, 3 11, 7, 15 0, || 8, 4 12, 2 10, 6, 14, 1;
长度为 16 的有序等价的连续片段(0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15)
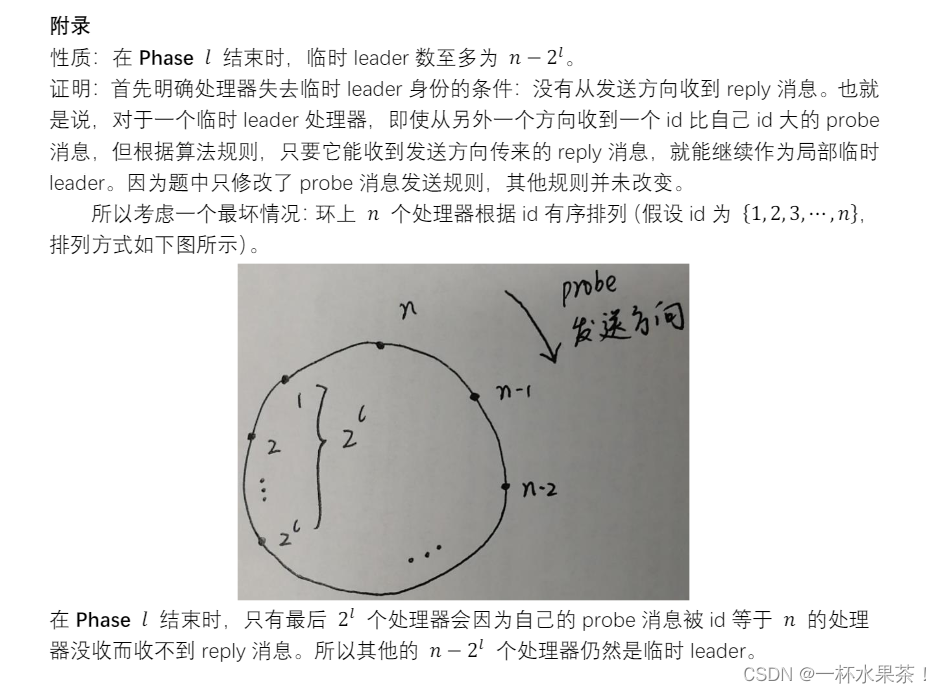
- 若将消息复杂度为 O(nlgn)的异步环选举算法(在阶段 1 向节点的 2 邻居发送 Prob 消息)修改为只向其中一个方向发送 Prob 消息,请问修改后算法的消息复杂度是多少?如何对其做进一步的修改使得消息复杂度仍然为 O(nlgn)。





算法题


设一个同步匿名的单向环有 n 个结点,每个结点均知道 n,每个节点的初始均状态相同,
每个结点上的程序相同且开始于同一时刻。
(1) 请问是否存在一个确定的算法选出一个 leader?简述理由。
(2) 试设计一个概率的 leader 选举算法。
(3) 请问你设计的概率算法属于哪一类算法?
(1) 对于同步环上的 leader 选举, 不存在非均匀的匿名算法。
- 初始状态相同:在一个匿名环中,处理器间始终保持对称,若无某种初始的非对称(如,
标识符唯一), 则不可能打破对称。 在匿名环算法里, 所有处理器开始于相同状态。 - 在同步系统中, 一个算法以轮的形式进行,根据引理 3.1 在环 R 上算法 A 的容许执行
里, 对于每一轮 k,所有处理器的状态在第 k 轮结束时是相同的。
由反证法,假设若在某轮结束时, 一个处理器宣布自己是 leader(进入选中状态), 则其它处理器亦同样如此, 这和 A 是一个 leader 选举算法的假定矛盾!
(2)算法由若干个 phase 构成,每个 phase 包括 n 轮,可用 phase 和轮控制算法流程。每
个结点可以设置一个随机数发生器 uniform(1…m),这里 m 是局部变量,初值等于 n。
每个结点上的随机数发生器 uniform(1…m)产生随机数𝑥𝑖当作自己的 id
在第 i 阶段开始
- 若一个结点的 id 是 i,则该结点绕环发送一个包含信息 i 的 msg;
- 若一结点的 id 不是 i, 且它收到一个 msg, 则它转发此 msg 后变为 non-leader,变成
non-leader 之后能转发 msg。 - 若一个结点的 id 是 i, 同时收到一个 msg,则本地变量 count 记录收到了多少个 msg。
id 为 i 的结点收到了 msg 数量,代表当前系统中产生了最小 id 的结点个数。此时 id 为 i 的结
点把 Phase 变为 1,m 变成 count。重新执行以上过程,直到 id 为 i 的结点只收到一个 msg,
此时该结点为 leader,同时绕环发送终止 msg,收到终止 msg 的 non-leader 终止运行。
(3)Las Vegas 算法。因为自己提出的算法一定能获得正确的解,但是随机算法可能会以极低的概率一直产生相同𝑥𝑖,导致不能产生最终解。
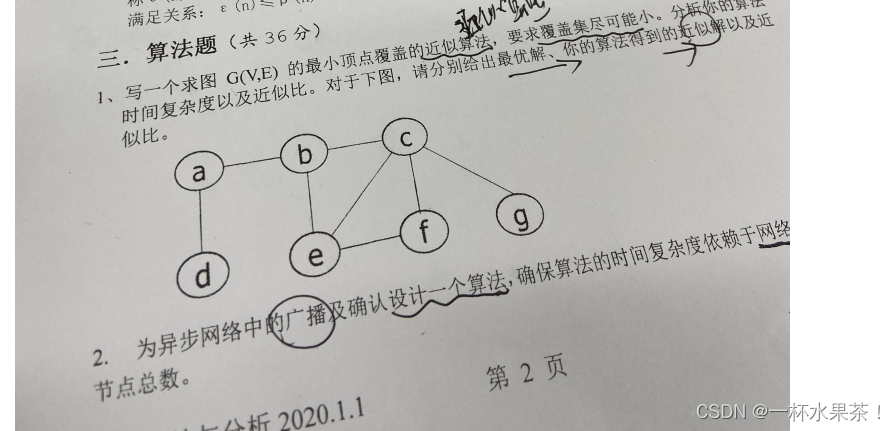

5.分布式系统中生成树构造问题:构造一棵具有 m 条边(信道总数),网络直径为 D 的生成
树,其构造方法是将 flooding 算法修改后得到的
(1)若设系统中处理器个数为 n,那么最坏情况下,异步算法完成生成树构造需要发送的
消息数是多少?
(2)基于异步算法找到该网络的一课生成树的时间复杂性、消息复杂性分别是多少?
(3)若在同步模型下进行生成树构造,其与异步算法的区别是什么?它构造的是 BFS 还是
DFS?请证明你的结果。



2013级试题


2019级试题



2021年秋

考卷





相关文章:

算法设计与分析--考试真题
分布式算法试题汇总选择题简答题算法题 2013级试题2019级试题2021年秋考卷 根据考试范围找相应题目做。 分布式算法试题汇总 选择题 下述说法错误的是___ A 异步系统中的消息延迟是不确定的 B 分布式算法的消息复杂性是指在所有合法的执行上发送消息总数的最大值 C 在一个异步…...
【鸿蒙学习笔记】页面和自定义组件生命周期
官方文档:页面和自定义组件生命周期 目录标题 [Q&A] 都谁有生命周期? [Q&A] 什么是组件生命周期? [Q&A] 什么是组件?组件生命周期 [Q&A] 什么是页面生命周期? [Q&A] 什么是页面?页面生…...

ASPICE与ISO 21434:汽车软件与网络安全标准的协同与互补
ASPICE(Automotive SPICE)与ISO 21434在汽车行业中存在显著的相关性,主要体现在以下几个方面: 共同目标: ASPICE和ISO 21434都旨在提高汽车系统和软件的质量、可靠性和安全性。ASPICE关注汽车软件开发过程的成熟度和…...
视频格式转换方法:如何使用视频转换器软件转换视频
众所周知,目前存在许多不同的视频和音频格式。但我们的媒体播放器、移动设备、PC 程序等仅兼容少数特定格式。例如,如果不先将其转换为 MP4、MOV 或 M4V 文件,AVI、WMV 或 MKV 文件就无法在 iPhone 上播放。 视频转换器允许您将一种视频格式…...

vim操作小诀窍:快速多行添加注释
在使用vim编译python代码的时候,经常碰到需要将一段代码注释的情况,每次都要按“向下” “向左”按钮,将光标移到句首,然后再键入#井号键。如果行数较多,则操作相当繁琐。 vim里面有将一段文字前面加#注释的方法&#…...

无线麦克风领夹哪个牌子好,2024年领夹麦克风品牌排行榜推荐
随着短视频热潮的兴起,越来越多的人倾向于用vlog记录日常生活,同时借助短视频和直播平台开辟了副业。在这一过程中,麦克风在近两年内迅速发展,从最初的简单收音功能演变为拥有多样款式和功能,以满足视频创作的需求。…...

Mybatis入门——语法详解:基础使用、增删改查、起别名、解决问题、注释、动态查询,从入门到进阶
文章目录 1.基础使用1.添加依赖2.在resouces文件下新建xml文件db.properties3.在resouces文件下新建xml文件mybatis-config-xml4.创建一个MybatisUtils工具类5.创建xml文件XxxMapper.xml映射dao层接口6.添加日志5.测试 2.增删改查1.select2.delete3.update4.insert5.模糊查询6.…...

仓库选址问题【数学规划的应用(含代码)】阿里达院MindOpt
本文主要讲述使用MindOpt工具优化仓库选址的数学规划问题。 视频讲解👈👈👈👈👈👈👈👈👈 一、案例场景 仓库选址问题在现代物流和供应链管理中具有重要的应用。因为仓库…...
Docker Compose 一键快速部署 RocketMQ
Apache RocketMQ是一个开源的分布式消息中间件系统,最初由阿里巴巴开发并贡献给Apache软件基金会。RocketMQ提供了高性能、高可靠性、高扩展性和低延迟的消息传递服务,适用于构建大规模分布式系统中的消息通信和数据同步。 RocketMQ支持多种消息模型&am…...
Vscode lanuch.json
Intro 使用launch.json 能够方便的运行需要传很多参数的代码文件 如下: import math import argparse # 1、导入argpase包def parse_args():parse argparse.ArgumentParser(descriptionCalculate cylinder volume) # 2、创建参数对象parse.add_argument(--rad…...

Golang开发:构建支持并发的网络爬虫
Golang开发:构建支持并发的网络爬虫 随着互联网的快速发展,获取网络数据成为了许多应用场景中的关键需求。网络爬虫作为一种自动化获取网络数据的工具,也因此迅速崛起。而为了应对日益庞大的网络数据,开发支持并发的爬虫成为了必…...
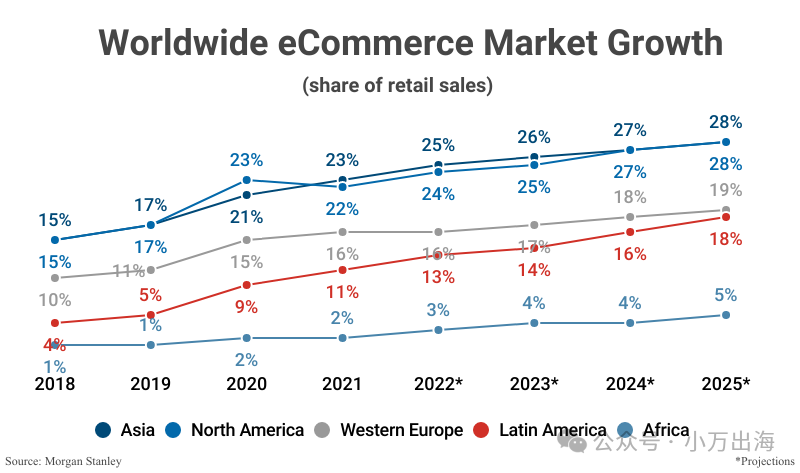
2024年跨境电商关键数据统计:市场规模将达到1.976万亿美元
预计2024年跨境电商消费市场规模将达到1.976万亿美元,占全球网上销售总额的31.2%。这一数据无疑展示了跨境电商市场的巨大潜力和迅猛增长趋势。 全球跨境电商的现状与未来 现状 2023年,全球跨境电商市场规模预计达到1.56万亿美元,占全球电子…...

联想至像M3070DNA打印机加粉及清零方法
基本参数: 产品类型:黑白激光多功能商用一体机(打印/复印/扫描) 网络功能:支持有线网络打印 最大处理幅面:A4 双面功能:自动 打印速度:30页/分钟(高速激光打印&…...

通过nginx去除 api url前缀 并保持后面剩余的url不变向后台请求
如 我前台浏览器向后台请求的接口是 http://127.0.0.1:5099/api/sample/sample/getbuttonlist 实际的请求接口传向 http://192.168.3.71:5099/sample/sample/getbuttonlist 方法是向config中加入下面这样一个server server {listen 5099;location /api/ {rewrite ^/a…...

AI技术在现代社会中的广泛应用及其影响
目录 前言: 一、AI技术在医疗领域的应用 二、AI技术在教育领域的应用 三、AI技术在工业领域的应用 四、AI技术在金融领域的应用 五、AI技术在生活领域的应用 前言: 随着科技的不断发展,人工智能(AI)技术逐渐成为人…...

VBA 批量变换文件名
1. 页面布局 在“main”Sheet中按照下面的格式编辑。 2. 实现代码 Private wsMain As Worksheet Private intIdx As LongPrivate Sub getExcelBookList(strPath As String)Dim fso As ObjectDim objFile As ObjectDim objFolder As ObjectSet fso = CreateObject("Scrip…...

OpenHarmony 5.0 纯血鸿蒙系统
OpenHarmony-v5.0-Beta1 版本已于 2024-06-20 发布。 OpenHarmony 5.0 Beta1 版本标准系统能力持续完善,ArkUI 完善了组件通过 C API 调用的能力;应用框架细化了生命周期管理能力,完善了应用拉起、跳转的能力;分布式软总线连接能力…...
)
计算机网络地址划分A-E(自学)
1、网络地址组成 (1)物理地址MAC(Media Access Control Address) 网卡生产商分配,全球唯一,48/64位二进制 (2)逻辑地址IP(Internet Protocol) 网络层地址,用于在不同网…...

js导入导出
好久没有学习新的知识点了,今天开始学一下前端的知识点。直接在vscode里面编写,然后从基本的前端知识开始。 JS的导入导出 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"…...
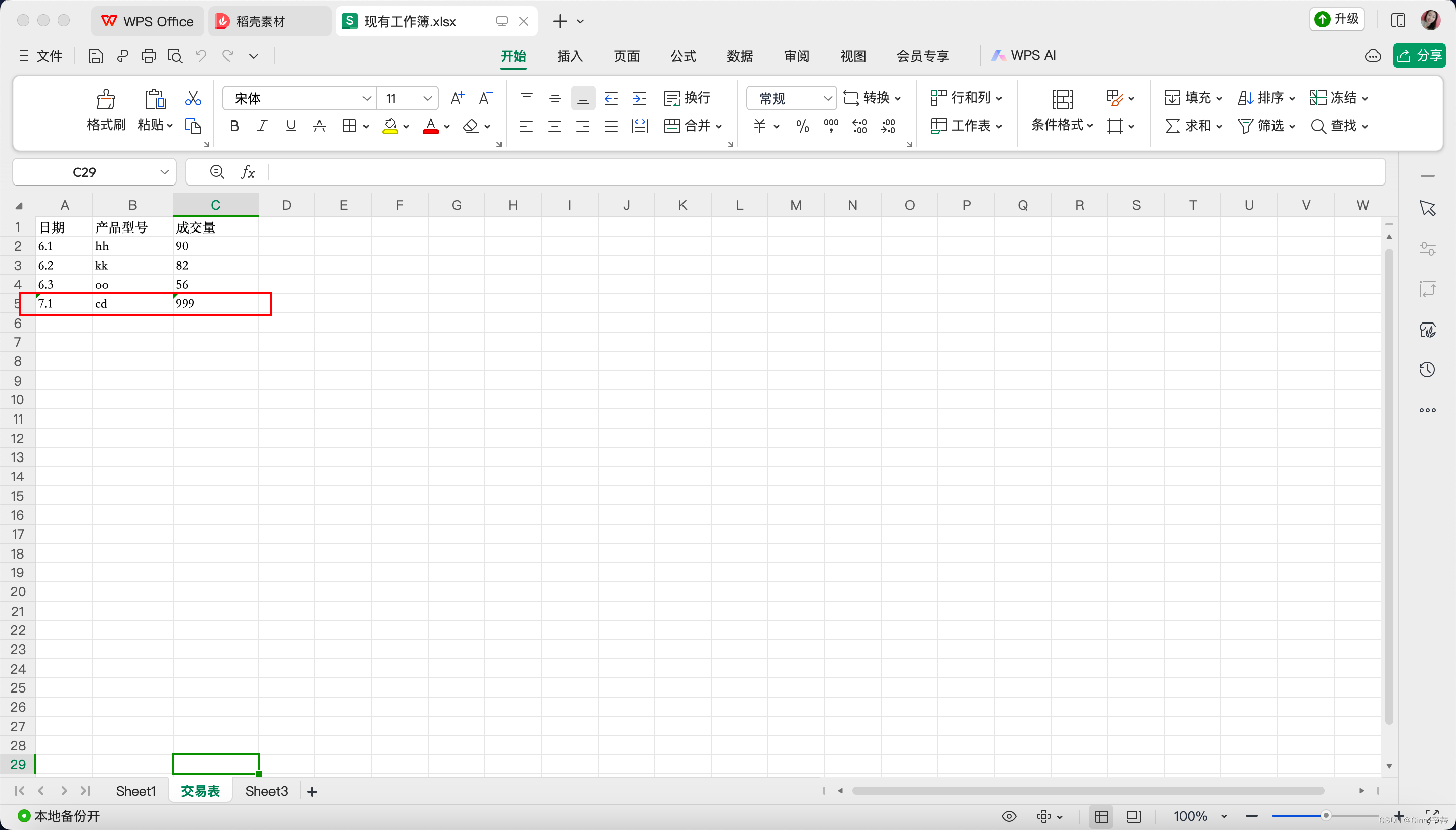
python办公自动化之excel
用到的库:openpyxl 实现效果:读取单元格的值,写入单元格 代码: import openpyxl # 打开现有工作簿 workbookopenpyxl.load_workbook(现有工作簿.xlsx) # 选择一个工作表 sheetworkbook[交易表] # 读取单元格的值 cell_valueshe…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
