前缀和总结
前缀和是一个常用的算法技巧,通常用于求解数组或序列的区间和。
具体来说,假设有一个长度为n的数组a,我们可以预处理出一个长度为n+1的前缀和数组s,其中s[i]表示原数组a前i个元素的和,即:
s[i] = a[0] + a[1] + ... + a[i-1]
这样一来,对于任意的区间[l, r],我们可以通过以下公式计算其和:
sum[l, r] = s[r+1] - s[l]
也就是说,sum[l, r]等于前缀和数组中r+1的值减去前缀和数组中l的值。这个公式的思想是,先计算区间右端点之前的所有元素的和s[r],再减去区间左端点之前的所有元素的和s[l-1],这样就可以得到区间[l, r]的和。
通过预处理前缀和数组,我们可以在O(1)的时间复杂度内计算任意区间的和,这在某些问题中非常有用,例如区间最大子段和问题、区间和的最大值/最小值等
实现
int[] preSum = new int[len + 1]; for (int l = 0; l < len; l++) for (int r = l; r < len; r++) // 区间和 [l, r],注意下标偏移if (preSum[r + 1] - preSum[l] == k) { // 前缀和为k//}上面将前缀和存储在一个数组中,如果需要去重,可以使用哈希表进行存储
相关文章:

前缀和总结
前缀和是一个常用的算法技巧,通常用于求解数组或序列的区间和。 具体来说,假设有一个长度为n的数组a,我们可以预处理出一个长度为n+1的前缀和数组s,其中s[i]表示原数组a前i个元素的和,即: s[i] = a[0] + a[1] + ... + a[i-1] 这样一来,对于任意的区间[l, r],我们可以…...

0109二分图-无向图-数据结构和算法(Java)
文章目录1 概念2 API3 分析和实现4 测试5 总结后记1 概念 二分图是一种能将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。 2 API public classBipartiteBipartite(Graph G)预处理函数public booleanisBipartitle()是否是二分图pub…...
)
计算机网络题库---选择题刷题训练(100多道精品)
第一章 概述 1.下列四项内容中,不属于Internet(因特网)基本功能是___D_____。 A.电子邮件 B.文件传输 C.远程登录 D.实时监测控制 2.Internet是建立在____C_____协议集上的国际互联网络。 A.IPX B.NetBEUI C.TCP/IP …...

16、字符串生成器
目录 (1)append()方法 (2)insert(int offset, arg)方法 (3)delete(int start , int end)方法 创建成功的字符串对象,其长度是固定的,内容不能被改变和编译。虽然使用“”可以达到…...

docker基本命令-容器
容器 基本概念 镜像(Image)和容器(Container)的关系,就像是面向对象程序设计中的 类 和 实例 一样,镜像是静态的定义,容器是镜像运行时的实体。容器可以被创建、启动、停止、删除、暂停等。 容…...
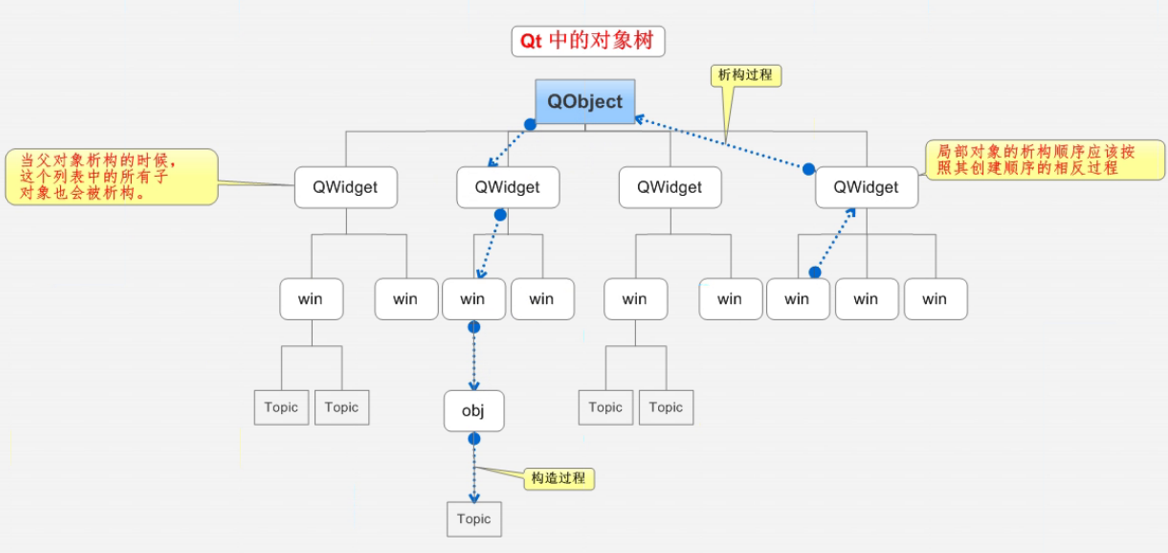
QT入门基础(一)
文章目录零.Qt背景1.什么是Qt2.Qt的发展史3.Qt的优势4.Qt应用一.第一个Qt程序0.项目创建1.main函数文件2.类头文件3.pro文件4.qt命名规范二.Qt按钮1.按钮创建和父子关系2.按钮常用api3.Qt窗口坐标体系4.对象树模型零.Qt背景 1.什么是Qt Qt是一个跨平台的C图形用户界面应用程序…...
WattOS:一个稳又快的轻量级 Linux 发行版
导读Linux 领域里的每个人不是听说过就是使用过某个轻量级的 Linux 发行版。大家都知道我们不断追求的是:占用内存少,配置资源要求低,包含一个轻量级的桌面环境(或者窗口管理器),并且提供和其他发行版相似的…...

Java调用Python脚本:轻松实现两种语言的互操作性
Java和Python都是非常流行的编程语言,它们都有自己的优点,但也有自己的局限性。在编写应用程序时,我们可能需要使用两种语言来共同完成一项任务。在这种情况下,Java需要调用Python脚本来解决某些问题,同时利用Java和Py…...
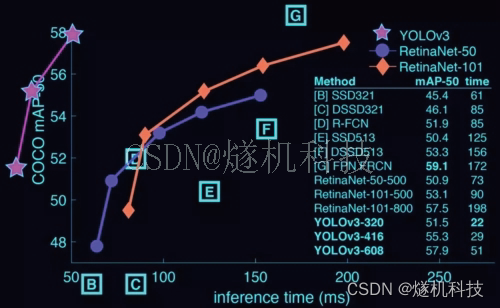
未系安全带识别系统 yolo
未系安全带识别系统通过pythonyolo智能视频分析技术,未系安全带识别算法对画面中高空作业人员未系安全带行为进行监测,未系安全带识别算法监测到人员未穿戴安全带时,立即通知后台人员及时处理触发告警。Yolo算法采用一个单独的CNN模型实现end…...
大白话MySQL是如何根据成本优化选择执行计划的?(上))
(七十六)大白话MySQL是如何根据成本优化选择执行计划的?(上)
之前已经给大家讲解清楚了 MySQL 在执行单表查询时候的一些执行计划,比如说const、ref、range、index、all之类的,也讲了多表关联的时候是如何执行的,本质其实就是先查一个驱动表,接着根据连接条件去被驱动表里循环查询࿰…...
DSRC技术
DSRC(Dedicated Short Range Communication)专用短程通信 定位 是V2X领域存在的两大通信技术之一(另一个为LTE-V2X)。 所属技术路线 与这两大技术相对应,是V2X无线通信技术的两大技术路线: IEEE 802.11p 本是04年指定的一个通…...

_面经问题_
一、Java编程语言 Java语言有哪些特点? JVM vs JDK vs JRE 什么是字节码? 采用字节码的好处是什么? 为什么不全部使用AOT呢? 为什么说Java语言"编译与解释并存"? Oracle JDK vs OpenJDK Java和C的区别? 注释有哪几种形式? 标识符和关键字的区别是什么? Jav…...
刷题记录(2023.3.6 - 2023.3.11)
我很喜欢这周的感觉,前两道题对着 wp 简略复现了一下,由于以前都是自己学习,对一些稍微多、稍微难的题都会马上避开,笨小孩逃避太久了,有些事逃不掉,总得面对,开始往往很难,多花点时…...
14 Day:同步锁与操作系统输入输出
前言:在上一期的线程章节中,我们的线程输出貌似有大问题,今天我们便要来学习同步锁来解决这个问题,同时再次基础上拿下键盘输入,实现操作系统的输入和输出。从今天开始我们的操作系统不在是一块“看板”了!…...

Gradle 的下载安装教程
Gradle 8.0.1 下载安装教程笔者的环境: Java 17.0.1 Gradle 8.0.1 Windows 10 教育版 64位 在继续阅读本教程之前,需要先完成 JDK 的安装。JDK 需要选择 8 及以上的版本。关于 JDK 的安装,可见笔者的另一篇博客: Java 的下载安…...

「Python 基础」常用模块
文章目录1. 内建模块datetimecollectionsnamedtuple()dequedefaultdictOrderedDictChainMapCounterbase64structhashlib摘要算法摘要的应用hmacitertoolscontextlib\_\_enter\_\_ 和 \_\_exit\_\_contextmanagerclosingurllibGETPOSTHandlerXMLDOMSAXHTMLParser2. 第三方模块Pi…...

Java【二叉搜索树和哈希表】详细图解 / 模拟实现 + 【Map和Set】常用方法介绍
文章目录前言一、二叉搜索树1、什么是二叉搜索树2、模拟实现二叉搜索树2.1, 查找2.2, 插入2.3, 删除3、性能分析二、模型三、哈希表1、什么是哈希表1.1, 什么是哈希冲突1.2, 避免, 解决哈希冲突1.2.1, 避免: 调节负载因子1.2.2, 解决1: 闭散列(了解)1.2.3, 解决2: 开散列/哈希桶…...

如何用 C 语言实现文本特征提取?
文本特征提取是一种将文本转换为数字或向量表示的技术,它是自然语言处理中的重要步骤。以下是一些用 C 语言实现文本特征提取的基本方法:基于词袋模型的特征提取词袋模型是一种将文本表示为单词频率的方法,可以通过以下步骤实现:将…...

ESD静电保护器件分类简介及场景应用
文章目录 1. ESD介绍1.1 ESD简介1.2 ESD产生原理1.3 ESD危害2. 器件级ESD模型2.1 人体模型(HBM)2.2 机器模型(MM)2.3 带电器件模型(CDM)3. 系统级ESD模型3.1 介绍3.2 防护器件分类简介3.2.1 TVS二极管3.2.2 MLCC陶瓷电容3.2.3 ESD抑制管3.2.4 MOV压敏电阻3.2.5 比较4. ES…...

硅谷银行倒闭的几点启示
摘要:本文从公开资料分析一下硅谷银行对信息科技行业的我们有一些什么启示。硅谷银行“拔网线”了,想创业的您,该注意了。1.硅谷银行是谁我们从其官网的说明来看看。The financial partner of the innovation economy.(翻译成中文…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

更新 Docker 容器中的某一个文件
🔄 如何更新 Docker 容器中的某一个文件 以下是几种在 Docker 中更新单个文件的常用方法,适用于不同场景。 ✅ 方法一:使用 docker cp 拷贝文件到容器中(最简单) 🧰 命令格式: docker cp <…...
