数据结构5---矩阵和广义表
一、矩阵的压缩存储
特殊矩阵:矩阵中很多值相同的元素并且它们的分布有一定的规律。
稀疏矩阵:矩阵中有很多零元素。压缩存储的基本思想是:
(1)为多个值相同的元素只分配一个存储空间;
(2)对零元素不分配存储空间。
1、特殊矩阵的压缩存储
(1)对称矩阵
只存储下三角部分的元素

存储结构
对于下三角的元素aij(i>=j),在数组中的下标与i,j关系为 k = i*(i-1)/2 + j-1
上三角的元素aij(i<j),因为aij = aji,则访问它的元素aji即可,即:k = j*(j-1)/2+i - 1
(2)三角矩阵
只存储上三角(或下三角)部分的元素
下三角矩阵
存储:
1.下三角元素 2.对角线上方的常数
矩阵中的任一元素aij在数组中的下标k与i,j的对应关系
当i>=j时 k=i*(i-1)/2+j-1
当i<j k=n*(n+1)/2
上三角矩阵
存储:
1.上三角元素 2.对角线下方的常数
矩阵中的任一元素aij在数组中的下标k与i,j的对应关系
当i<=j时 k=(i-1)*(2n-i+2)/2+j-1
当i>j k=n*(n+1)/2
(3)对角矩阵
对角矩阵:所有非零元素都集中在以主对角线为中心的带状区域中,除了主对角线和它的上下方若干条对角线的元素外,所有其他元素都为零。

(4)稀疏矩阵

我们定义了一个三元组
struct Triple
{int row,col; //行和列DataType item; //值
};三元组表:将稀疏矩阵的非零元素对应的三元组所构成的集合,按行优先的顺序排列成一个线性表。
采用顺序存储结构存储三元组表

三元顺序表的存储结构定义
const int MAX = 100;
struct SparseMatrix
{struct Triple data[MAX]; //存储非零元素int mu,nu,num; //行数,列数,非零元素个数
};这种存储方法的缺点是:进行矩阵加法、减法等操作时,非零元素的个数和位置都会发生变化,顺序存储法就非常不方便了。
2、十字链表
采用链接存储结构存储三元组表,每个非零元素对应的三元组存储为一个链表结点,结构为:
| row | col | item |
| down | right | |
row:存储非零元素的行号
col:存储非零元素的列号
item:存储非零元素的值
right:指针域,指向同一行中的下一个三元组
down:指针域,指向同一列中的下一个三元组

定义结构体
#define ElementType inttypedef struct OLNode
{int row;//1~mint col;//1~nElementType value;struct OLNode *right, *down;//非零元素所在行,列后继链域
}OLNode, *OLink;typedef struct CrossList
{OLink* row_head, *col_head;//行,列链表的头指针向量int m;//行数int n;//列数int len;//非零元素个数
}CrossList;代码实现
//稀疏矩阵的链式存储结构:十字链表
#include <stdio.h>
#include <stdlib.h>
#include <string.h>#define ElementType inttypedef struct OLNode
{int row;//1~mint col;//1~nElementType value;struct OLNode *right, *down;//非零元素所在行,列后继链域
}OLNode, *OLink;typedef struct CrossList
{OLink* row_head, *col_head;//行,列链表的头指针向量int m;//行数int n;//列数int len;//非零元素个数
}CrossList;void CreatCrossList(CrossList* M, int m, int n, int len)
{M->m = m;M->n = n;M->len = len;if(!(M->row_head = (OLink*)malloc((m + 1) * sizeof(OLink)))){perror("row_head");exit(-1);}if(!(M->col_head = (OLink*)malloc((n + 1) * sizeof(OLink)))){perror("col_head");exit(-1);}memset(M->row_head, 0, (m + 1) * sizeof(OLink));memset(M->col_head, 0, (n + 1) * sizeof(OLink));//初始化为空链表int i = 0, j = 0, e = 0;//结点的行,列,值printf("请输入结点的行号,列号,值:\n");while(len){scanf("%d %d %d", &i, &j, &e);if(i < 1||i > m||j < 1||j > n){printf("行列号不合法,请重新输入:\n");continue;}int flag = 0;//检查位置是否重复for(OLNode* k = M->row_head[i]; k != NULL; k = k->right){if(k->col == j)flag = 1;}if(flag){printf("结点位置重复,请重新输入:\n");continue;}OLNode* p = (OLNode*)malloc(sizeof(OLNode));//申请结点if(p == NULL){perror("Node application");exit(-1);}p->row = i; p->col = j; p->value = e;p->right = p->down = NULL;//行链表插入if(M->row_head[i] == NULL)//该行还没有结点{M->row_head[i] = p;}else if(p->col < M->row_head[i]->col)//新建结点列号<该行首结点列号{p->right = M->row_head[i];M->row_head[i] = p;}else//寻找插入位置{OLNode* q;for(q = M->row_head[i]; q->right && q->right->col < j; q = q->right);p->right = q->right;q->right = p;}//列链表插入if(M->col_head[j] == NULL)//该列还没有结点{M->col_head[j] = p;}else if(p->row < M->col_head[j]->row)//新建结点行号<改行首节点行号{p->down = M->col_head[j];M->col_head[j] = p;}else//寻找插入位置{OLNode* q;for(q = M->col_head[j]; q->down && q->down->row < i; q = q->down)p->down = q->down;p->down = p;}len--;printf("插入成功!\n");printf("请输入结点的行号,列号,值:\n");}}void PrintCrossList(CrossList* M)//打印十字链表
{for(int row = 0; row < M->m; row++){OLNode* p = M->row_head[row];while(p != NULL){printf("(%d, %d)=%d ", p->row, p->col, p->value);p = p->right;}printf("\n");}
}int main()
{CrossList M;CreatCrossList(&M, 10, 10, 10);PrintCrossList(&M);return 0;
}3、快速转置
在顺序结构里转置
(1)简单转置
按矩阵source的列序进行转置

算法实现
SparseMatrix source,dest;
int q = 1;
for(col=1;col<=source.nu;col++)
{for(p=1;p<=source.num;p++){if(source.data[p].col==col){dest.data[q].row = source.data[p].col;dest.data[q].col = source.data[p].row;dest.data[q].e = source.data[p].e;q++;}}}(2)快速转置
按矩阵source的行序进行转置

方法:增加2个辅助向量


这里的cPos[col]为:1 3 5 7 8 8 9

-3一定是第一个,12一定是第三个....
cPos算法:
cPos[1] = 1;
for(col = 2;col <= source.nu; col++)
{cPos[col] = cPos[col-1]+cNum[col-1];
}cNum算法:
for(col = 1;col <= source.nu; ++col) cNum[col]=0; //初始化全为0
for(sPos = 1;sPos <= source.number;++sPos)++cNum[source.data[sPos].col]; //就是按列遍历整个三元组,列号为几,就在对应的cNum上++
就是找位置,找到对应位置后,其相应的cPs+1
二、广义表
1、定义
广义表又称列表,也是一种线性存储结构,通数组类似,广义表中即可存储不可再分的元素也能存储可在分元素。
例如:数组中可以存储‘a’、3这样的字符或数字,也能存储数组,比如二维数组、三维数组,数组都是可在分成子元素的。广义表也是如此,但与数组不同的是,在广义表中存储的数据是既可以再分也可以不再分的,形如:{1,{1,2,3}}。
广义表记作:
LS = (a1,a2,…,an)
2、原子和子表
广义表中存储的单个元素称为 "原子",而存储的广义表称为 "子表"。
例如创建一个广义表 LS = {1,{1,2,3}},我们可以这样解释此广义表的构成:广义表 LS 存储了一个原子 1 和子表 {1,2,3}。
以下是广义表存储数据的一些常用形式:
- A = ():A 表示一个广义表,只不过表是空的。
- B = (e):广义表 B 中只有一个原子 e。
- C = (a,(b,c,d)) :广义表 C 中有两个元素,原子 a 和子表 (b,c,d)。
- D = (A,B,C):广义表 D 中存有 3 个子表,分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。
- E = (a,E):广义表 E 中有两个元素,原子 a 和它本身。这是一个递归广义表,等同于:E = (a,(a,(a,…)))。
注意,A = () 和 A = (()) 是不一样的。前者是空表,而后者是包含一个子表的广义表,只不过这个子表是空表。
3、表头和表尾
当广义表不是空表时,称第一个数据(原子或子表)为"表头",剩下的数据构成的新广义表为"表尾"。
强调一下,除非广义表为空表,否则广义表一定具有表头和表尾,且广义表的表尾一定是一个广义表。
例如在广义表中 LS={1,{1,2,3},5} 中,表头为原子 1,表尾为子表 {1,2,3} 和原子 5 构成的广义表,即 {{1,2,3},5}。
再比如,在广义表 LS = {1} 中,表头为原子 1 ,但由于广义表中无表尾元素,因此该表的表尾是一个空表,用 {} 表示。
4、广义表的存储结构
使用顺序表实现广义表结构,不仅需要操作 n 维数组(例如 {1,{2,{3,4}}} 就需要使用三维数组存储),还会造成存储空间的浪费。

typedef struct GLNode{int tag;//标志域union{char atom;//原子结点的值域struct{struct GLNode * hp,*tp;}ptr;//子表结点的指针域,hp指向表头;tp指向表尾}subNode;
}*Glist;这里用到了 union 共用体,因为同一时间此节点不是原子节点就是子表节点,当表示原子节点时,就使用 atom 变量;反之则使用 ptr 结构体。
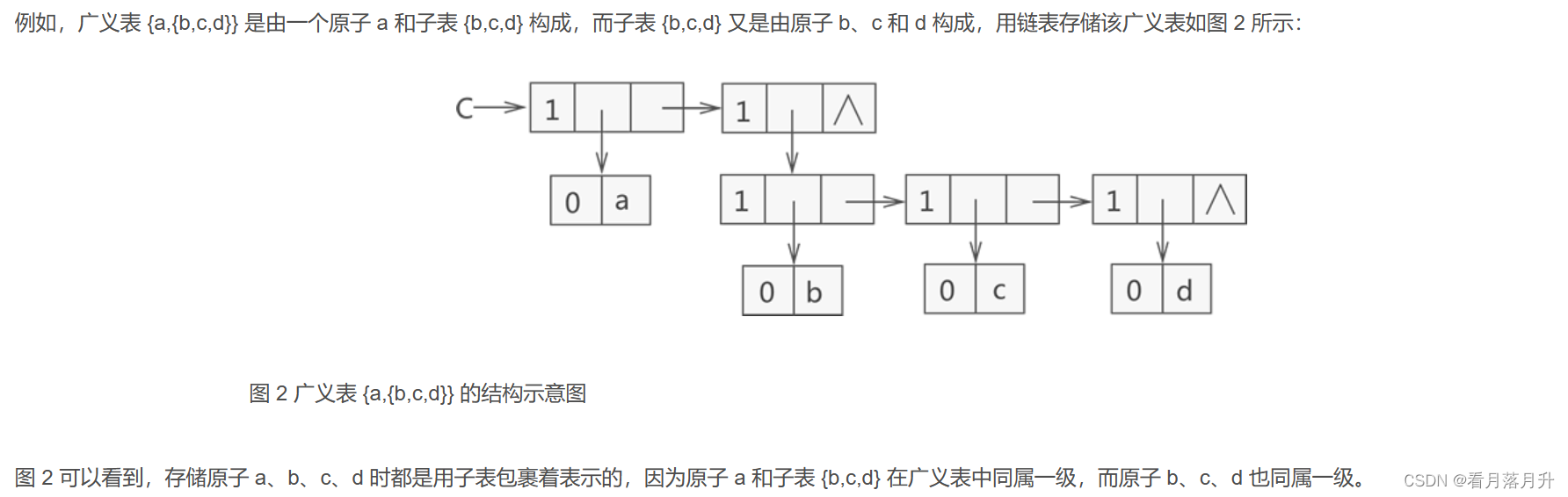
Glist creatGlist(Glist C) {//广义表CC = (Glist)malloc(sizeof(Glist));C->tag = 1;//表头原子‘a’C->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));C->subNode.ptr.hp->tag = 0;C->subNode.ptr.hp->subNode.atom = 'a';//表尾子表(b,c,d),是一个整体C->subNode.ptr.tp = (Glist)malloc(sizeof(Glist));C->subNode.ptr.tp->tag = 1;C->subNode.ptr.tp->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));C->subNode.ptr.tp->subNode.ptr.tp = NULL;//开始存放下一个数据元素(b,c,d),表头为‘b’,表尾为(c,d)C->subNode.ptr.tp->subNode.ptr.hp->tag = 1;C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.hp->tag = 0;C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.hp->subNode.atom = 'b';C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp = (Glist)malloc(sizeof(Glist));//存放子表(c,d),表头为c,表尾为dC->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->tag = 1;C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.hp->tag = 0;C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.hp->subNode.atom = 'c';C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp = (Glist)malloc(sizeof(Glist));//存放表尾dC->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->tag = 1;C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->subNode.ptr.hp = (Glist)malloc(sizeof(Glist));C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->subNode.ptr.hp->tag = 0;C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->subNode.ptr.hp->subNode.atom = 'd';C->subNode.ptr.tp->subNode.ptr.hp->subNode.ptr.tp->subNode.ptr.tp->subNode.ptr.tp = NULL;return C;
}4、长度
广义表的长度,指的是广义表中所包含的数据元素的个数。
由于广义表中可以同时存储原子和子表两种类型的数据,因此在计算广义表的长度时规定,广义表中存储的每个原子算作一个数据,同样每个子表也只算作是一个数据。
例如,在广义表 {a,{b,c,d}} 中,它包含一个原子和一个子表,因此该广义表的长度为 2。
再比如,广义表 {{a,b,c}} 中只有一个子表 {a,b,c},因此它的长度为 1。
前面我们用 LS={a1,a2,...,an} 来表示一个广义表,其中每个 ai 都可用来表示一个原子或子表,其实它还可以表示广义表 LS 的长度为 n。广义表规定,空表 {} 的长度为 0。
5、深度
由于这个不做考试内容,分享一个博客
数据结构-广义表-CSDN博客![]() https://blog.csdn.net/qq_51701007/article/details/126352030?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522171894059816800211521274%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=171894059816800211521274&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-126352030-null-null.142%5Ev100%5Epc_search_result_base5&utm_term=%E5%B9%BF%E4%B9%89%E8%A1%A8&spm=1018.2226.3001.4187
https://blog.csdn.net/qq_51701007/article/details/126352030?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522171894059816800211521274%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=171894059816800211521274&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-126352030-null-null.142%5Ev100%5Epc_search_result_base5&utm_term=%E5%B9%BF%E4%B9%89%E8%A1%A8&spm=1018.2226.3001.4187
相关文章:
数据结构5---矩阵和广义表
一、矩阵的压缩存储 特殊矩阵:矩阵中很多值相同的元素并且它们的分布有一定的规律。 稀疏矩阵:矩阵中有很多零元素。压缩存储的基本思想是: (1)为多个值相同的元素只分配一个存储空间; (2)对零元素不分配存储空间。 1、特殊矩阵的压缩存储 (1)对称矩…...

jquery使用infinitescroll无线滚动+自定义翻页
jquery版本 jquery-1.8.3.js infinitescroll版本 2.0.0 如果infinitescroll版本最新的jquery版本也要用新的 接口用nodejs jquery.infinitescroll.js官网地址 前端代码《接口返回JSON数据》 <!DOCTYPE html> <html lang"en"> <head><meta cha…...

【漏洞复现】锐捷统一上网行为管理与审计系统——远程命令执行漏洞
声明:本文档或演示材料仅供教育和教学目的使用,任何个人或组织使用本文档中的信息进行非法活动,均与本文档的作者或发布者无关。 文章目录 漏洞描述漏洞复现测试工具 漏洞描述 锐捷统一上网行为管理与审计系统naborTable/static_convert.php…...

通义灵码上线 Visual Studio 插件市场啦!
通义灵码,是阿里云出品的一款基于通义大模型的智能编码辅助工具,提供行级/函数级实时续写、自然语言生成代码、单元测试生成、代码优化、注释生成、代码解释、研发智能问答、异常报错排查等能力,提供代码智能生成、研发智能问答能力。 通义灵…...
:客观题真题集)
GESP 四级急救包(2):客观题真题集
客观题真题集 一、选择题1. 真题梳理2. 真题答案3. 重难点点播(1) 指针和地址(2) 时间复杂度 二、判断题1. 真题梳理2. 真题答案 一、选择题 1. 真题梳理 若函数声明为 void f(int &a, int b, const int &c),且在主函数内已经声明了 x , y , z x,y,z x,y,…...

VERYCLOUD睿鸿股份确认参展2024年ChinaJoy BTOB商务洽谈馆,期待与你相聚
作为在全球数字娱乐领域兼具知名度与影响力的年度盛会,2024年第二十一届ChinaJoy将于7月26日至7月29日在上海新国际博览中心盛大召开,本届展会主题为:初心“游”在,精彩无限!(Stay True, Game On.ÿ…...

Java面试题:讨论Spring框架的核心组件,如IoC容器、AOP、事务管理等
Spring框架是一个功能强大且灵活的Java企业级应用开发框架,其核心组件包括以下几个主要部分: 1. IoC容器(Inversion of Control Container) IoC容器是Spring框架的核心部分,用于管理应用程序的依赖注入(D…...

【方案】基于5G智慧工业园区解决方案(PPT原件)
5G智慧工业园区整体解决方案旨在通过集成5G通信技术、物联网、大数据和云计算等先进技术,实现园区的智能化、高效化和绿色化。 该方案首先构建高速、稳定的5G网络,确保园区内设备、人员与物流的实时连接和高效沟通。其次,通过工业物联网技术&…...

使用System.currentTimeMillis获取当前时间
使用System.currentTimeMillis获取当前时间 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来探讨Java中如何使用System.currentTimeMillis()方法来获取…...
手机远程控制另一台手机的全新使用教程(安卓版)
看完这篇文章,你可以了解到安卓手机如何远程控制安卓手机,以及苹果手机如何远程控制安卓手机。 如果想要用安卓手机远程管控苹果手机,或者苹果手机远程管控另一台苹果手机,请点击查看视频《手机远程管控另一台手机的全新使用教程…...
商城积分系统的代码实现(上)-- 积分账户及收支记录
一、背景 上一系列文章,我们说了积分的数模设计及接口设计,接下里,我们将梳理一下具体的代码实现。 使用的语言的java,基本框架是spring-boot,持久化框架则是Jpa。 使用到的技术点有: 分布式锁…...

【C++进阶9】异常
一、C语言传统的处理错误的方式 终止程序,如assert 如发生内存错误,除0错误时就会终止程序返回错误码 需要程序员自己去查找对应的错误 z如系统的很多库的接口函数都是通 过把错误码放到errno中,表示错误 二、C异常概念 异常:函…...

RecyclerVIew->加速再减速的RecyclerVIew平滑对齐工具类SnapHelper
XML文件 ItemView的XML文件R.layout.shape_item_view <?xml version"1.0" encoding"utf-8"?> <FrameLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"100dp"android:layout_heig…...
突破SaaS产品运营困境:多渠道运营如何集中管理?
随着数字化时代的到来,SaaS(软件即服务)产品已成为企业日常运营不可或缺的工具。然而,在竞争激烈的市场环境下,SaaS产品运营越来越重视多渠道、多平台布局,以更广泛地触及潜在用户,然而…...

智能语音热水器:置入NRK3301离线语音识别ic 迈向智能家居新时代
一、热水器语音识别芯片开发背景 在科技的今天,人们对于生活品质的追求已不仅仅满足于基本的物质需求,更渴望通过智能技术让生活变得更加便捷、舒适。热水器作为家庭生活中不可或缺的一部分,其智能化转型势在必行。 在传统热水器使用中&#…...
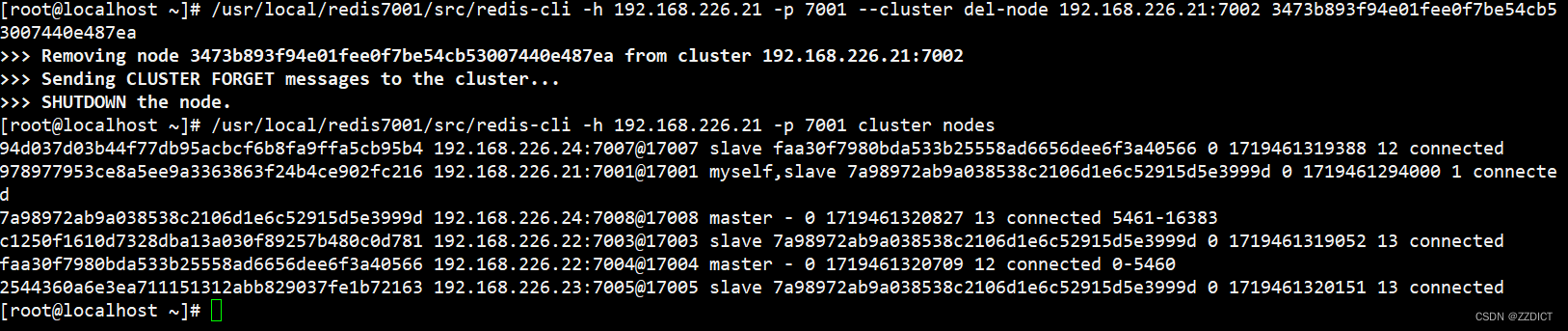
Redis集群部署合集
目录 一. 原理简述 二. 集群配置 2.1 环境准备 2.2 编译安装一个redis 2.3 创建集群 2.4 写入数据测试 实验一: 实验二: 实验三: 实验四: 添加节点 自动分配槽位 提升节点为master: 实验…...

【HDFS】关于Hadoop的IPC.Client类的一些整理
org.apache.hadoop.ipc.Client 类是IPC服务的一个客户端。 IPC请求把一个Writable对象当做参数,返回一个Writable对象当做结果value。 一个IPC服务运行在某个端口上,并且由参数class和value class定义。 Router里的IPC.Client对象就两个 有这样一个类:ClientCache 看名字就…...

Swoole v6 能否让 PHP 再次伟大?
现状 传统的 PHP-FPM 也是多进程模型的的运行方式,但每个进程只能处理完当前请求,才能接收下一个请求。而且对于 PHP 脚本来说,只是接收请求和响应请求,并不参与网络通信。对数据库资源的操作,也是一次请求一次有效&am…...

C++ STL Iterator Adapter
1. std::back_insert_iterator 使用 // back_insert_iterator example #include <iostream> // std::cout #include <iterator> // std::back_insert_iterator #include <vector> // std::vector #include <algorithm> // std::copy…...

android-aidl5
aidl类是实现Manager和Service通信的桥梁。 例如在修改Android Wifi功能的时候看到WifiManager管理WifiService; AIDL是一种android内部进程通信接口的描述语言,通过它我们可以定义进程间的通信接口。 比如onclick(),用oneway修…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
