核方法(kernel Method)
核方法
核方法定义
一种能够将在原始数据空间中的非线性数据映射到高维线性可分的方法。
核方法的用处
1、低维数据非线性,当其映射到高维空间(feature space)时,可以用线性方法对数据进行处理。
2、线性学习器相对于非线性学习器有更好的过拟合控制从而可以更好地保证泛化性能,同时,利用核函数将非线性映射隐含在线性学习器中进行同步计算,使得计算复杂度与高维特征空间的维数无关。
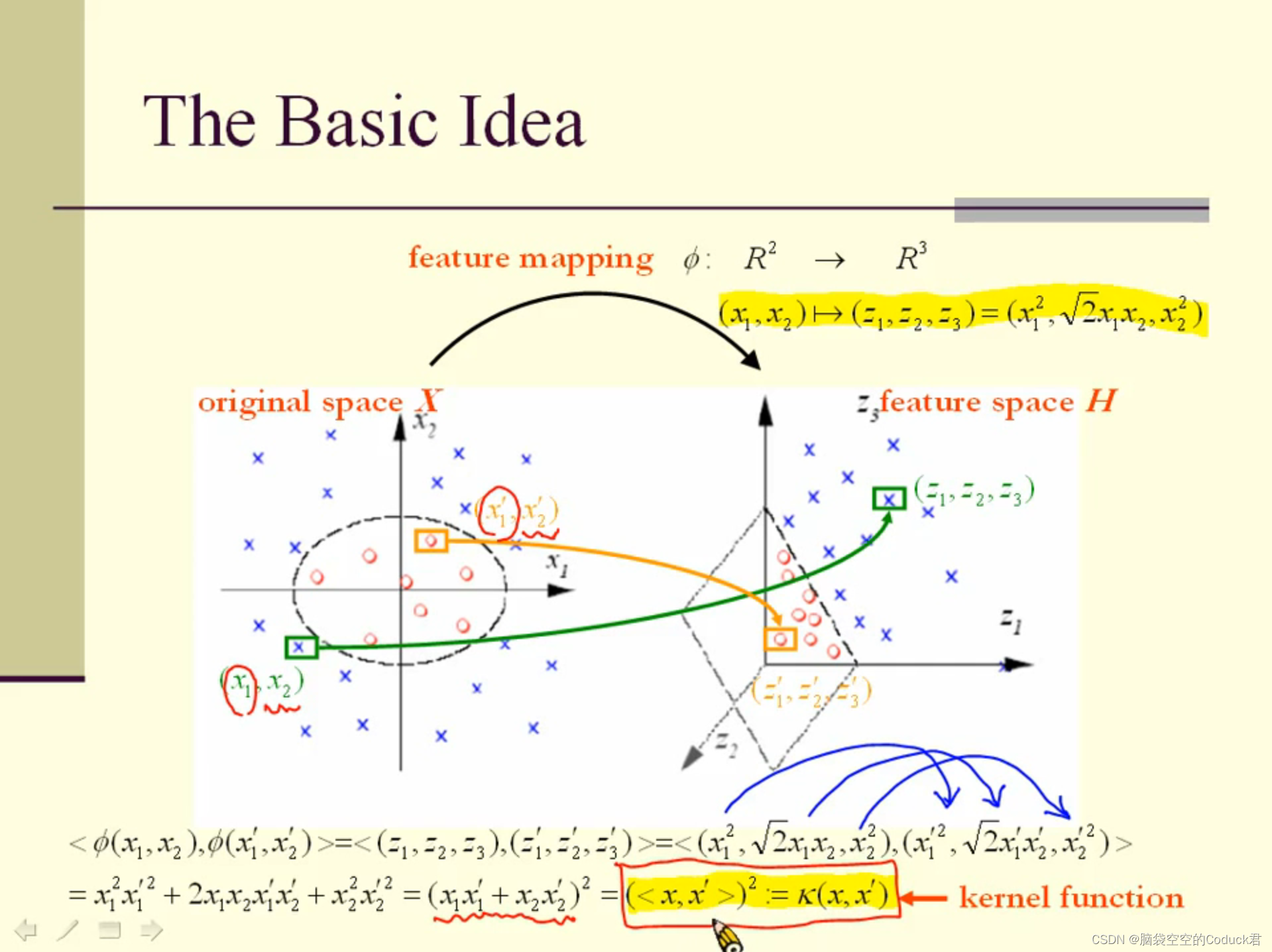
如上,是将二维空间的非线性数据通过ϕ\phiϕ,把数据映射到了三维空间中。
并且我们发现,在高维空间中两个数据的内积,是原空间中对应数据的函数
(如上的<ϕ(x1,x2)>,<ϕ(x1′,x2′)>=(<x,x′>)2<\phi(x_1,x_2)>,<\phi(x_1',x_2')>=(<x,x'>)^{2}<ϕ(x1,x2)>,<ϕ(x1′,x2′)>=(<x,x′>)2),该函数被定义为K(x,x′)K(x,x')K(x,x′),称为核函数(将原始空间中的向量作为输入向量,并返回特征空间(转换后的数据空间,可能是高维)中向量的点积的函数称为核函数)。
注意:将数据映射到不同的高维空间,其对应的核函数不同。
核函数作用
1、通过K(x,x′)K(x,x')K(x,x′)我们可以直接计算出在feature space(高维空间)中点的两点间的距离平方和两个向量间的角度。

2、由于可以通过1中的方法计算出高维空间的距离和角度,我们完全可以不去计算出ϕ\phiϕ(一般ϕ\phiϕ难计算),可由K(x,x′)K(x,x')K(x,x′)直接处理高维空间的数据。
3、避免在高维空间运作,选择一个特征空间,其中点积可以使用输入空间中的非线性函数直接求值,降低了计算的复杂度(在高维空间中考虑的维数过多,计算也相当复杂)。
核矩阵
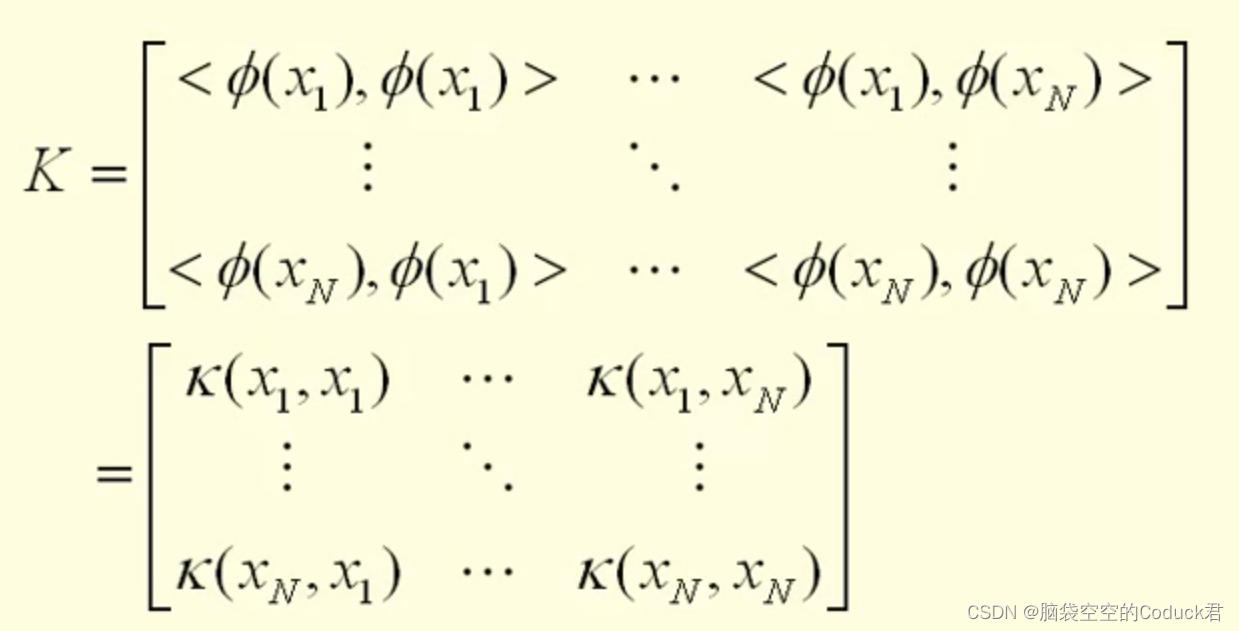
核函数要满足的条件
有限正半定(给定任意有限 n个点(x1~xn),求解其矩阵是正定的)
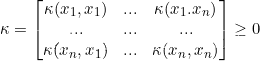
常用核函数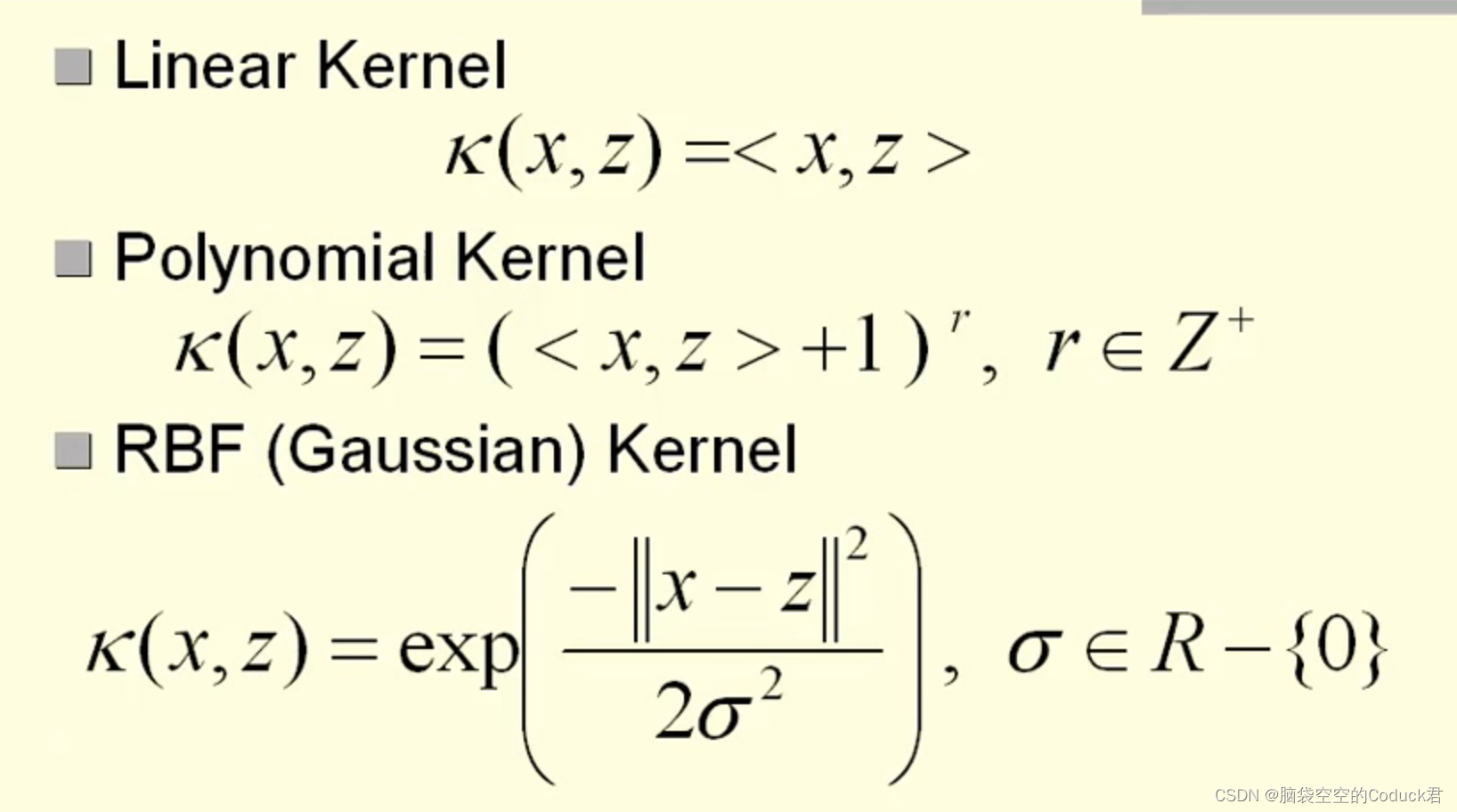
K(x,xi)K(x,x_i)K(x,xi)与ϕ\phiϕ的关系
●只要知道kernel function,φ就不是必须的
●只要知道kernel function就可以达到计算需求
●有限半正定的kernel matrix可以使用
●k和φ是一一对应的
●知道kernel function 可以构建feature space
简单例子
yiy_iyi是标签,只有两个类别+1和-1,然后利用φ将x映射到更高维空间φ ( x ),下面就是投影之后的空间。同时计算出不同类别数据的两个中心点
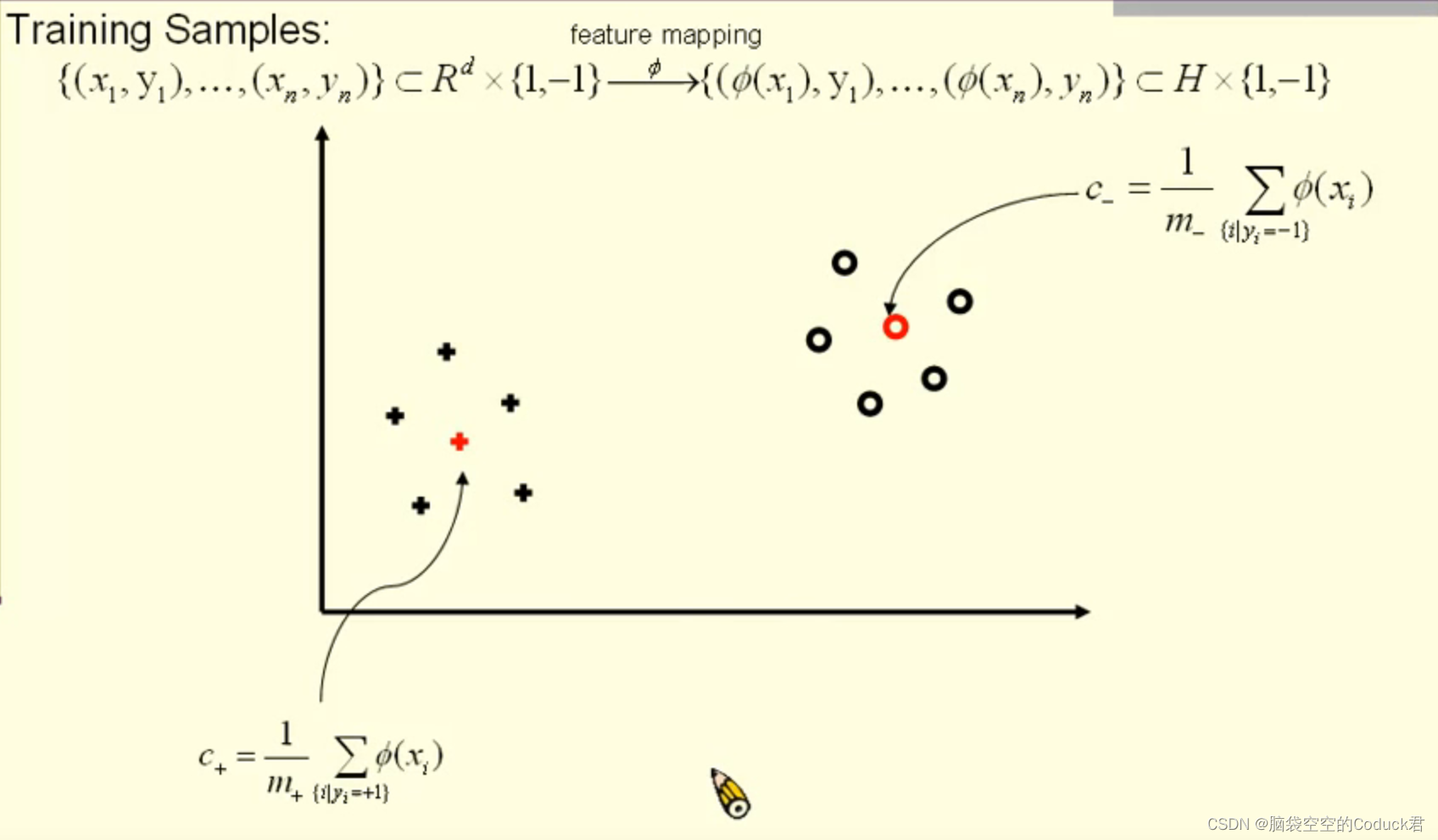
然后计算出中垂线,通过新数据向量ϕ(x)\phi(x)ϕ(x)与向量w的所成角来判断新数据的类别
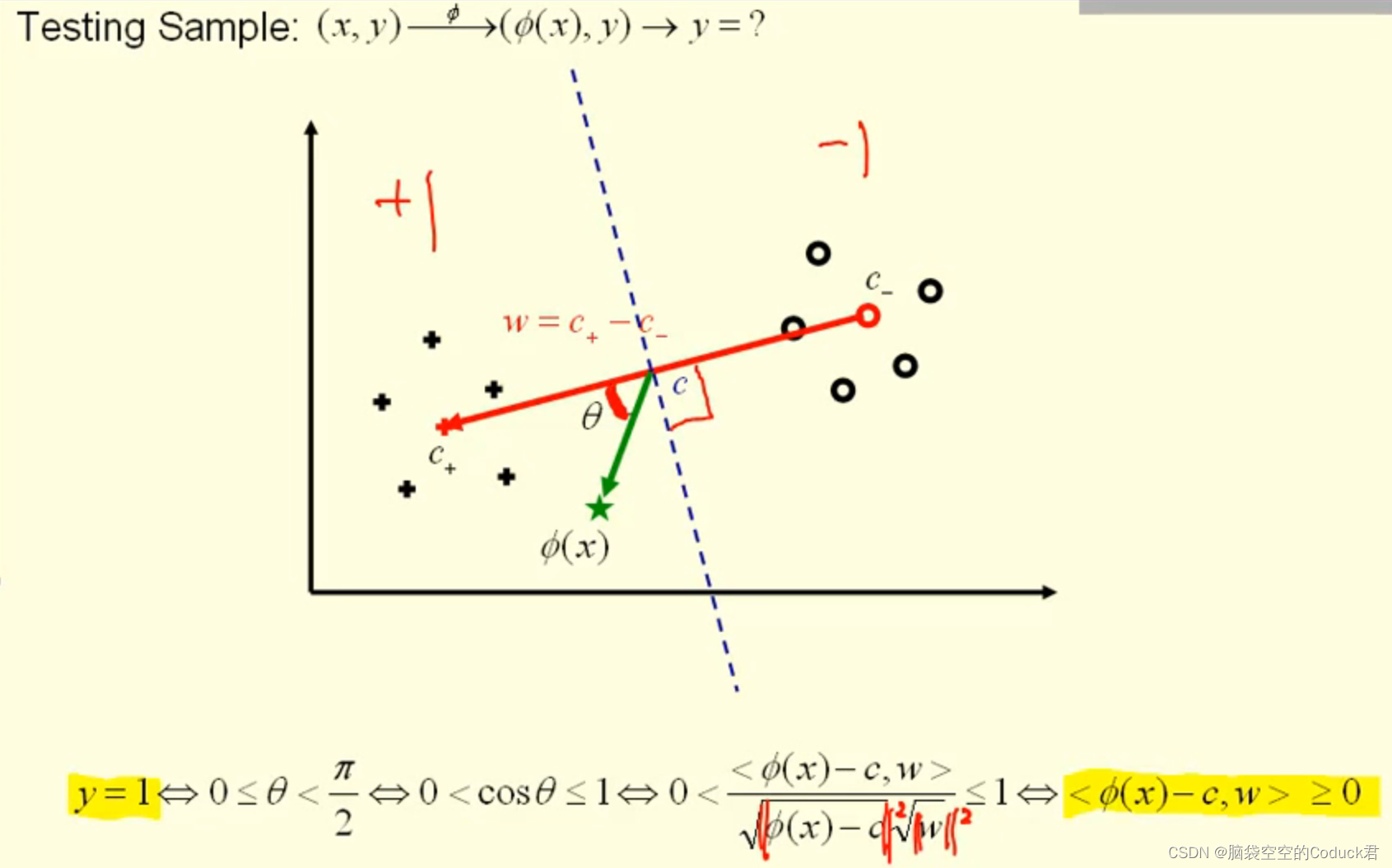
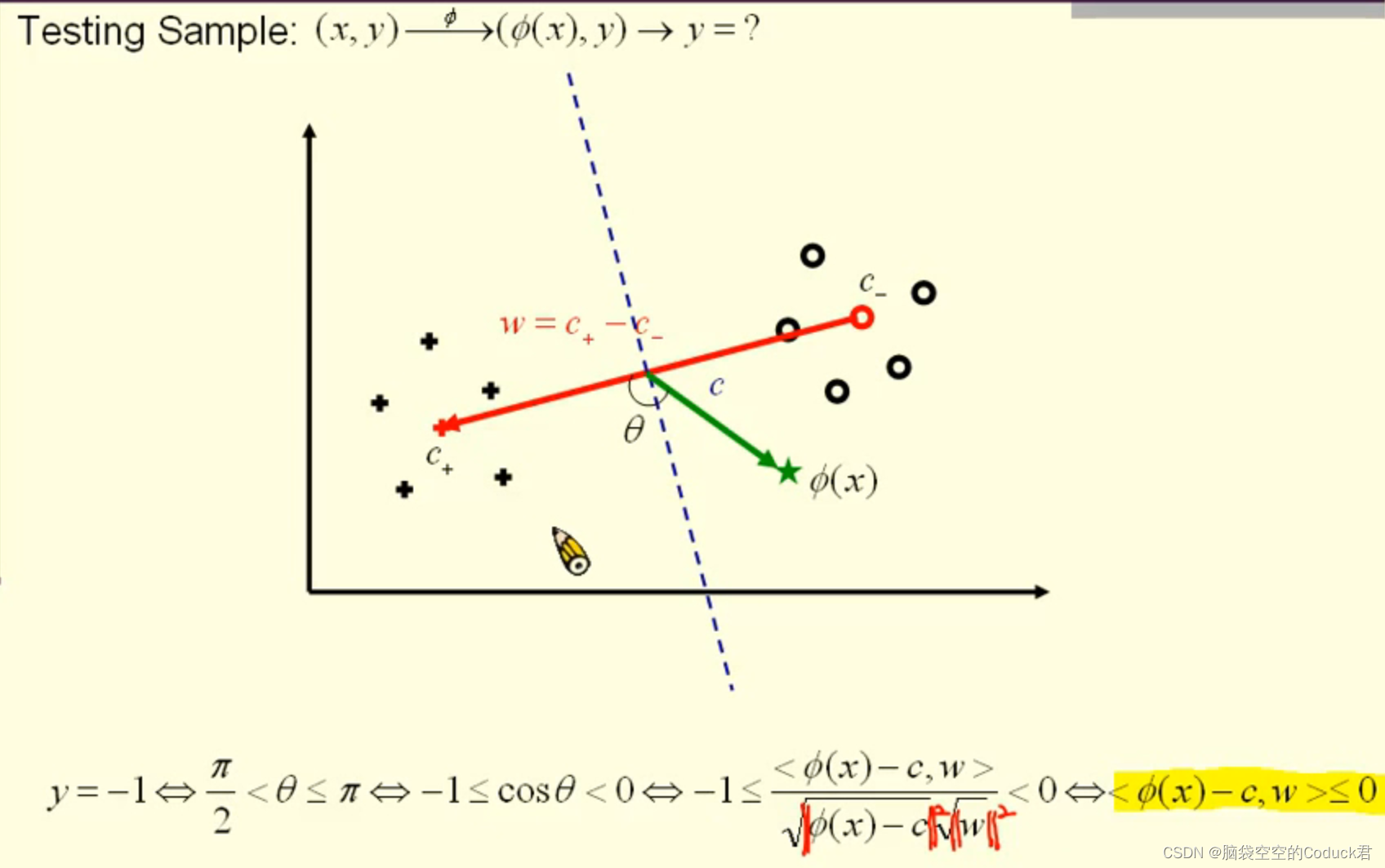
由上面知,可以通过sign函数来判断新数据类别
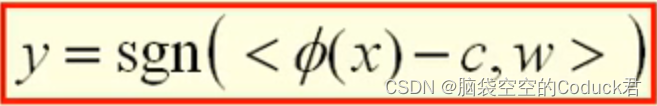
以下是<ϕ(x)−c,w><\phi(x)-c,w><ϕ(x)−c,w>的计算方法,同样是可以用核函数来表示

Dual Representation
我们还可以用线性表达式来表示上面的式子
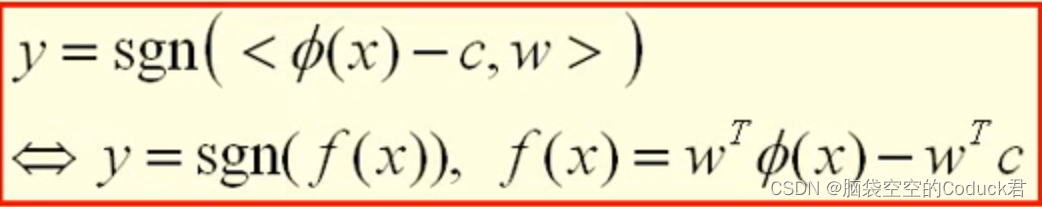


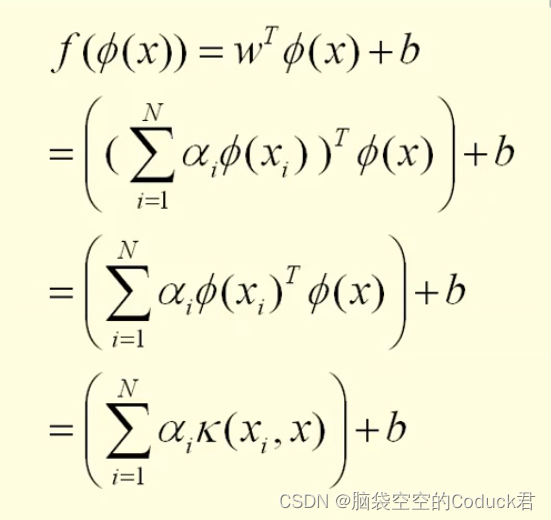
相关文章:
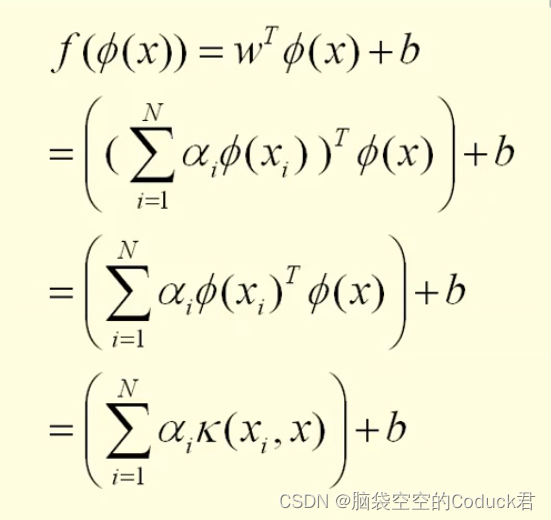
核方法(kernel Method)
核方法 核方法定义 一种能够将在原始数据空间中的非线性数据映射到高维线性可分的方法。 核方法的用处 1、低维数据非线性,当其映射到高维空间(feature space)时,可以用线性方法对数据进行处理。 2、线性学习器相对于非线性学…...
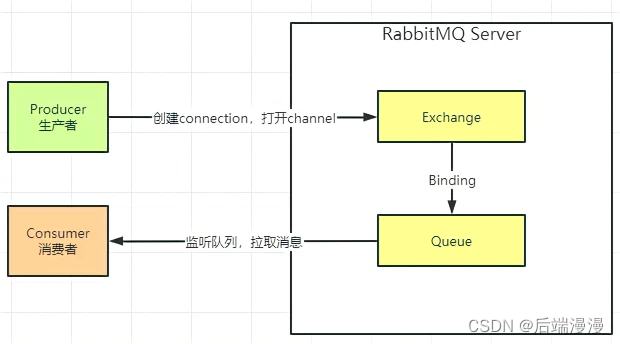
消息队列MQ用来做什么的,市场上主流的四大MQ如何选择?RabbitMQ带你HelloWorld!
文章目录MQ用来做什么的MQ会有什么样的麻烦MQ消息队列模式分类MQ消息队列常用协议市场主流四大MQRabbitMQ项目开发RabbitMQ中的组成部分MQ用来做什么的 省流 :系统解耦、异步调用、流量削峰 系统解耦 首先举例下面这个场景,现有ABCDE五个系统ÿ…...
2023年中国高校计算机大赛-团队程序设计天梯赛(GPLT)上海理工大学校内选拔赛(同步赛) A — E
2023年中国高校计算机大赛-团队程序设计天梯赛(GPLT)上海理工大学校内选拔赛(同步赛) 文章目录A -- A Xor B Problem题目分析codeB -- 吃苹果题目分析codeC -- n皇后问题题目分析codeD -- 分苹果题目分析codeE -- 完型填空题目分析codeA – A…...

一文分析Linux v4l2框架
说明: Kernel版本:4.14 ARM64处理器,Contex-A53,双核 使用工具:Source Insight 3.5, Visio 1. 概述 V4L2(Video for Linux 2):Linux内核中关于视频设备驱动的框架,对上向应用层提供…...
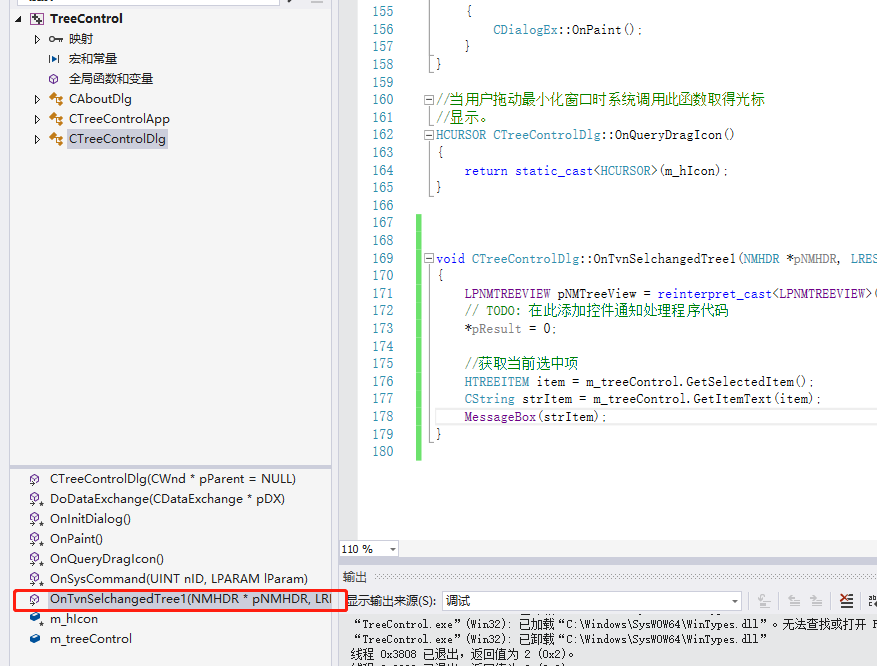
MFC常用控件使用(文本框、编辑框、下拉框、列表控件、树控件)
简介 本文章主要介绍下MFC常用控件的使用,包括静态文本框(Static Text)、编辑框(Edit Control)、下拉框(Combo Box)、列表控件(List Control)、树控件(Tree Control)的使用。 创建项目 我们选择 文件->新建->新建项目,选择MFC程序 选择基于对话…...

13 node 程序后台执行加上 tail 命令, 中断 tail 命令, 同时也中断了 node 程序
前言 呵呵 最近帮朋友解决问题[2022.09.08] 需要启动一个 node 程序, 然后 需要一个 startUp.sh 脚本 然后 反手写了一个过去, 按道理 来说 应该是 后台启动了对应的 node 程序, 然后将 标准输出, 错误输出 输出到 logs/nohup.log 日志文件中, 然后基于 tail 命令 来查看 …...
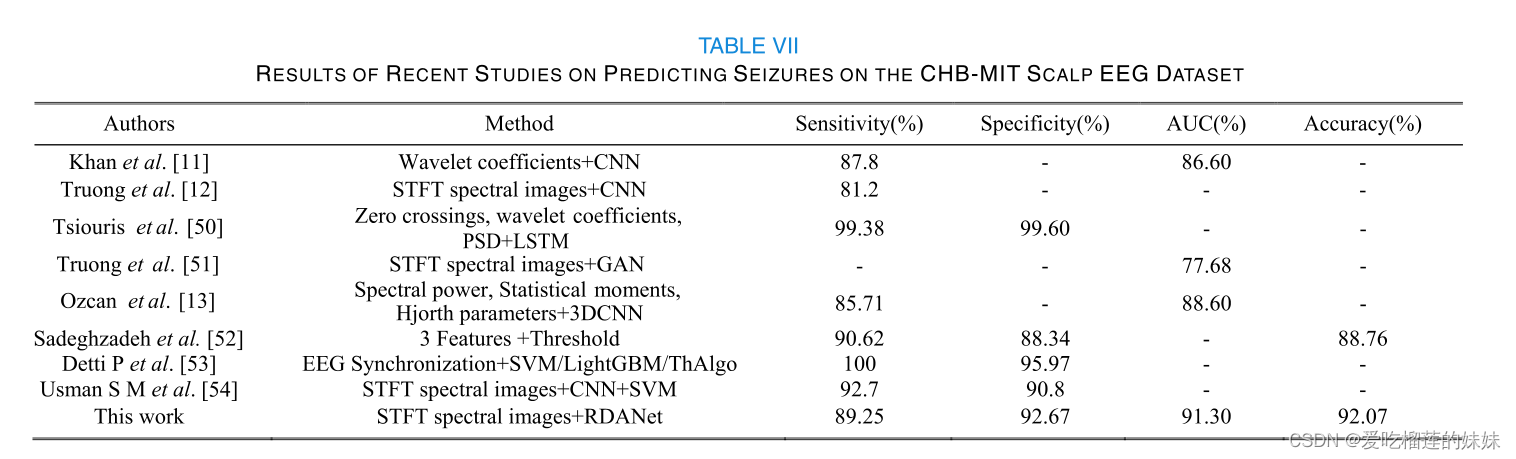
52癫痫发作预测的有效双自注意力残差网络
Effective dual self-attentional residual networks for epileptic seizure prediction 摘要 癫痫发作预测作为慢性脑疾病中最具挑战性的数据分析任务之一,引起了众多研究者的广泛关注。癫痫发作预测,可以在许多方面大大提高患者的生活质量࿰…...

【计算机网络】Tcp IP 面试题相关
互联网协议群(TCP/IP):多路复用是怎么回事? 1.【问题】IPv4 和 IPv6 有什么区别? IPv4 是用 32 位描述 IP 地址,理论极限约在 40 亿 IP 地址; IPv6 是用 128 位描述 IP 地址,IPv6 可…...

【MySQL】MySQL的存储引擎
目录 概念 分类 操作 概念 数据库存储引擎是数据库底层软件组织,数据库管理系统(DBMS)使用数据引擎进行创建、查 询、更新和删除数据。 不同的存储引擎提供不同的存储机制、索引技巧、锁定水平等功能。现在 许多不同的数据库管理系统…...

es6动态模块import()
目录 一、语法说明 二、适用场合 三、注意点 四、示例代码 五、效果 一、语法说明 import命令会被 JavaScript 引擎静态分析,先于模块内的其他语句执行(import命令叫做“连接” binding 其实更合适)。 // 报错 if (x 2) {import MyMod…...
)
【Flask】Jinja2模板(十四)
Jinja2是一个单独的Python包,Flask依赖Jinja2,安装Flask时会自动安装Jinja2。Jinja2可以将数据和模板结合在一起生成动态文本。 一、引入 来看一个最简单的视图函数: app.route(/) def hello_world():return Hello World! 这个…...

Mr. Cappuccino的第49杯咖啡——冒泡APP(升级版)之基于Docker部署Gitlab
冒泡APP(升级版)之基于Docker部署Gitlab基于Docker安装Gitlab登录Gitlab创建Git项目上传代码使用Git命令切换Git地址使用IDE更换Git地址基于Docker安装Gitlab 查看beginor/gitlab-ce镜像版本 下载指定版本的镜像 docker pull beginor/gitlab-ce:11.3.0…...
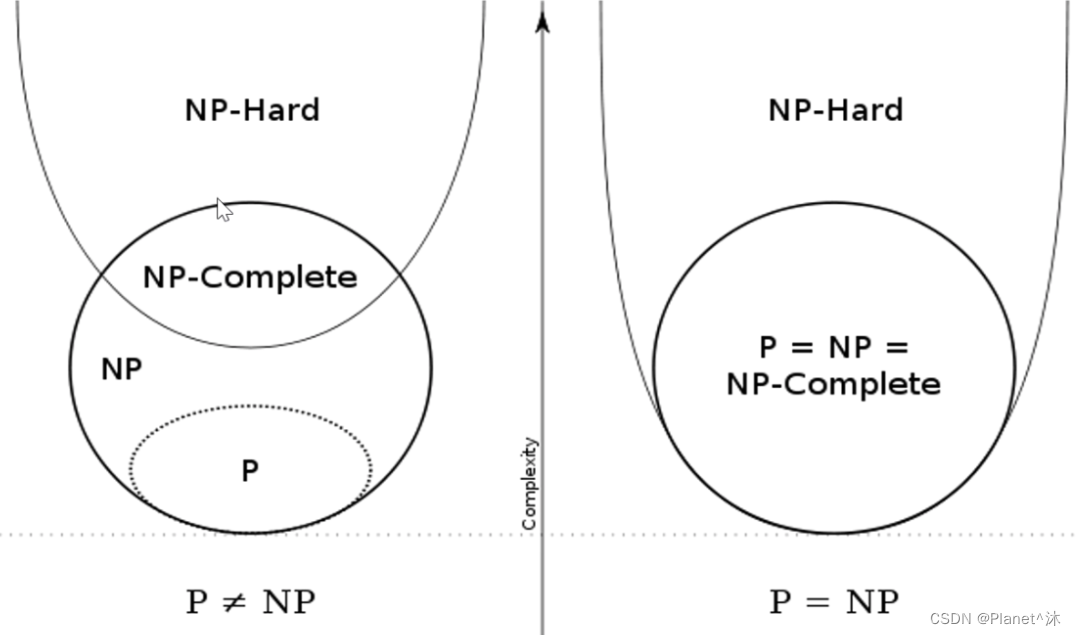
《机器学习》基础概念之【P问题】与【NP问题】
《机器学习》基础概念之【P问题】与【NP问题】 这里写目录标题《机器学习》基础概念之【P问题】与【NP问题】一、多项式&时间复杂度1.1. 多项式1.2.时间复杂度二、P问题 & NP问题2.1. P问题2.2.NP问题2.3.举例理解NP问题-TSP旅行商推销问题三、NP-hard问题&NP-C问题…...

WinRAR安装教程
文章目录WinRAR安装教程无广告1. 下载2. 安装3. 注册4. 去广告WinRAR安装教程无广告 1. 下载 国内官网:https://www.winrar.com.cn/ 2. 安装 双击,使用默认路径: 点击“安装”。 点击“确定”。 点击“完成”。 3. 注册 链接ÿ…...
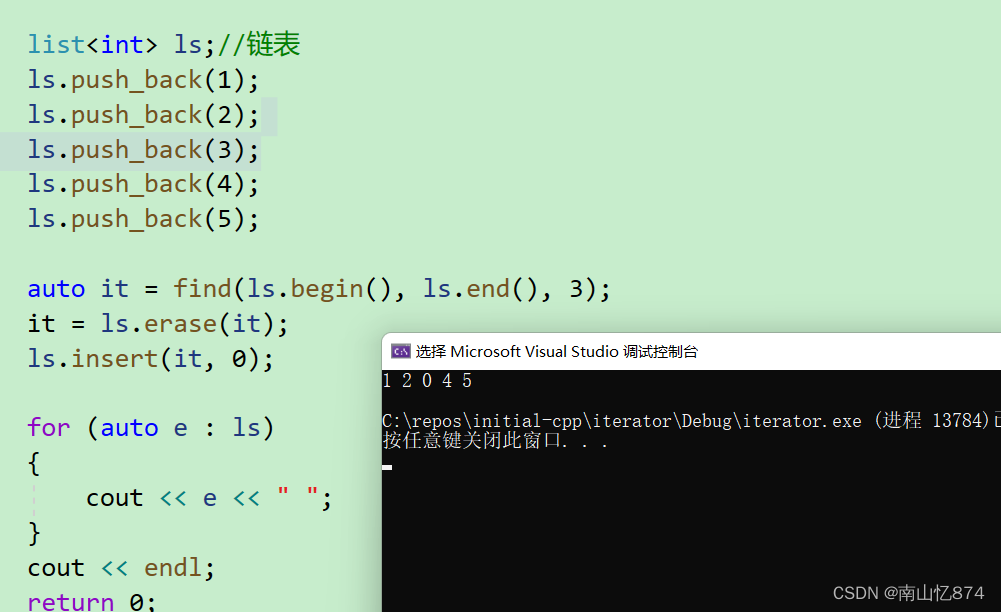
C++:vector和list的迭代器区别和常见迭代器失效问题
迭代器常见问题的汇总vector迭代器和list迭代器的使用vector迭代器list迭代器vector迭代器失效问题list迭代器失效问题vector和list的区别vector迭代器和list迭代器的使用 学习C,使用迭代器和了解迭代器失效的原因是每个初学者都需要掌握的,接下来我们就…...

SpringSecurity如何实现前后端分离
前后端分离模式是指由前端控制页面路由,后端接口也不再返回html数据,而是直接返回业务数据,数据一般是JSON格式。Spring Security默认的表单登录方式,在未登录或登录成功时会发起页面重定向,在提交登录数据时ÿ…...

为ubuntu 18.04添加蓝牙驱动
目录背景方法背景 从网上买的能直接插ubuntu 1804的usb蓝牙太少了,而且还贵。我就直接从JD下单的一个便宜的USB蓝牙,结果插上机器没有驱动起不来。我的PC是个3年前的老机器,实在是不想升级系统,于是捣鼓半天捣鼓好了,…...

Stable Diffusion Prompt用法
Stable Diffusion可以根据你输入的提示词(prompt)来绘制出想象中的画面。 1、正向提示词(Prompt): 提高图像质量的prompt: prompt用途HDR, UHD, 64K(HDR、UHD、4K、8K和64K)这样的质量词可以带来巨大的差异提升照片…...

jenkins问题
目录 python 不是内部或外部命令,也不是可运行的程序 ‘cmd’ 不是内部或外部命令,也不是可运行的程序或批处理文件。 git 不是内部或外部命令,也不是可运行的程序或批处理文件。 pywintypes.com_error: (-2147024891, ‘拒绝访问。’, None,…...

阅读笔记DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks
zi,t∈Rz_{i,t}\in \mathbb{R}zi,t∈R表示时间序列iii在ttt时刻的值。给一个连续时间段t∈[1,T]t\in [1, T]t∈[1,T],将其划分为context window[1,t0)[1,t_0)[1,t0)和prediction window[t0,T][t_0,T][t0,T]。用context window的时间序列预测prediction window…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
