[信号与系统]模拟域中的一阶低通滤波器和二阶滤波器
前言
不是学电子出身的,这里很多东西是问了朋友…
模拟域中的一阶低通滤波器传递函数
模拟域中的一阶低通滤波器的传递函数可以表示为:
H ( s ) = 1 s + ω c H(s) = \frac{1}{s + \omega_c} H(s)=s+ωc1
这是因为一阶低通滤波器的设计目标是允许低频信号通过,同时衰减高频信号。具体来说,它的频率响应特性决定了这个形式的传递函数。
1. 传递函数的来源
一阶低通滤波器的传递函数来源于它的微分方程描述。考虑一个简单的RC(电阻-电容)电路:
- 电阻 R R R
- 电容 C C C
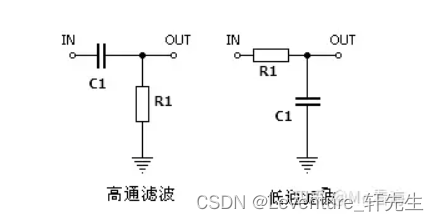
高通滤波器
对于高通滤波器电路(左图),我们有一个电容 C 1 C_1 C1 和一个电阻 R 1 R_1 R1:
-
阻抗计算:
- 电容的阻抗 Z C = 1 j ω C 1 Z_C = \frac{1}{j\omega C_1} ZC=jωC11
- 电阻的阻抗 Z R = R 1 Z_R = R_1 ZR=R1
-
电路分析:
- 输入电压 V i n V_{in} Vin 加在电容和电阻的串联上。
- 输出电压 V o u t V_{out} Vout 在电阻上。
使用分压公式:
V o u t = V i n ⋅ Z R Z R + Z C = V i n ⋅ R 1 R 1 + 1 j ω C 1 = V i n ⋅ R 1 ⋅ j ω C 1 1 + j ω R 1 C 1 V_{out} = V_{in} \cdot \frac{Z_R}{Z_R + Z_C} = V_{in} \cdot \frac{R_1}{R_1 + \frac{1}{j\omega C_1}} = V_{in} \cdot \frac{R_1 \cdot j\omega C_1}{1 + j\omega R_1 C_1} Vout=Vin⋅ZR+ZCZR=Vin⋅R1+jωC11R1=Vin⋅1+jωR1C1R1⋅jωC1
所以,传递函数 H ( s ) H(s) H(s) 是:
H ( s ) = V o u t V i n = j ω R 1 C 1 1 + j ω R 1 C 1 = s R 1 C 1 1 + s R 1 C 1 H(s) = \frac{V_{out}}{V_{in}} = \frac{j\omega R_1 C_1}{1 + j\omega R_1 C_1} = \frac{s R_1 C_1}{1 + s R_1 C_1} H(s)=VinVout=1+jωR1C1jωR1C1=1+sR1C1sR1C1
令 ω c = 1 R 1 C 1 \omega_c = \frac{1}{R_1 C_1} ωc=R1C11,则传递函数为:
H ( s ) = s / ω c 1 + s / ω c H(s) = \frac{s / \omega_c}{1 + s / \omega_c} H(s)=1+s/ωcs/ωc
低通滤波器
对于低通滤波器电路(右图),我们有一个电阻 R 1 R_1 R1 和一个电容 C 1 C_1 C1:
-
阻抗计算:
- 电阻的阻抗 Z R = R 1 Z_R = R_1 ZR=R1
- 电容的阻抗 Z C = 1 j ω C 1 Z_C = \frac{1}{j\omega C_1} ZC=jωC11
-
电路分析:
- 输入电压 V i n V_{in} Vin 加在电阻和电容的串联上。
- 输出电压 V o u t V_{out} Vout 在电容上。
使用分压公式:
V o u t = V i n ⋅ Z C Z R + Z C = V i n ⋅ 1 j ω C 1 R 1 + 1 j ω C 1 = V i n ⋅ 1 j ω R 1 C 1 + 1 V_{out} = V_{in} \cdot \frac{Z_C}{Z_R + Z_C} = V_{in} \cdot \frac{\frac{1}{j\omega C_1}}{R_1 + \frac{1}{j\omega C_1}} = V_{in} \cdot \frac{1}{j\omega R_1 C_1 + 1} Vout=Vin⋅ZR+ZCZC=Vin⋅R1+jωC11jωC11=Vin⋅jωR1C1+11
所以,传递函数 H ( s ) H(s) H(s) 是:
H ( s ) = V o u t V i n = 1 1 + j ω R 1 C 1 = 1 1 + s R 1 C 1 H(s) = \frac{V_{out}}{V_{in}} = \frac{1}{1 + j\omega R_1 C_1} = \frac{1}{1 + s R_1 C_1} H(s)=VinVout=1+jωR1C11=1+sR1C11
令 ω c = 1 R 1 C 1 \omega_c = \frac{1}{R_1 C_1} ωc=R1C11,则传递函数为:
H ( s ) = 1 1 + s / ω c H(s) = \frac{1}{1 + s / \omega_c} H(s)=1+s/ωc1
微分方程形式
这个电路的微分方程可以写为:
V o u t ( t ) = 1 R C ∫ − ∞ t V i n ( τ ) e − t − τ R C d τ V_{out}(t) = \frac{1}{RC} \int_{-\infty}^{t} V_{in}(\tau) e^{-\frac{t - \tau}{RC}} d\tau Vout(t)=RC1∫−∞tVin(τ)e−RCt−τdτ
通过拉普拉斯变换,将其转化到频域:
V o u t ( s ) V i n ( s ) = 1 R C ⋅ s + 1 \frac{V_{out}(s)}{V_{in}(s)} = \frac{1}{RC \cdot s + 1} Vin(s)Vout(s)=RC⋅s+11
令 ω c = 1 R C \omega_c = \frac{1}{RC} ωc=RC1,得到:
H ( s ) = 1 s + ω c H(s) = \frac{1}{s + \omega_c} H(s)=s+ωc1
2. 频率响应
一阶低通滤波器的传递函数 H ( s ) H(s) H(s) 表示了滤波器对不同频率信号的响应:
- 当 s = j ω s = j\omega s=jω 时,低频( ω \omega ω 较小)信号通过的幅度接近 1,即通过率高。
- 当 ω \omega ω 较大时,传递函数的值接近 0,即高频信号被大大衰减。
3. 截止频率
ω c \omega_c ωc 是滤波器的截止频率,即在该频率处信号的幅度被衰减到原来的 1 2 \frac{1}{\sqrt{2}} 21 倍(约 0.707 倍)。它定义了低通滤波器允许通过的最大频率。
综上所述,模拟域中的一阶低通滤波器传递函数为:
H ( s ) = 1 s + ω c H(s) = \frac{1}{s + \omega_c} H(s)=s+ωc1
是由其设计目标、微分方程描述以及频率响应特性决定的。
二阶滤波器通过联级一阶滤波器的推导
二阶滤波器可以通过两个一阶滤波器串联(联级)得到。假设我们有两个一阶低通滤波器,其传递函数分别为:
H 1 ( s ) = 1 1 + s / ω c 1 H_1(s) = \frac{1}{1 + s / \omega_{c1}} H1(s)=1+s/ωc11
H 2 ( s ) = 1 1 + s / ω c 2 H_2(s) = \frac{1}{1 + s / \omega_{c2}} H2(s)=1+s/ωc21
当将这两个一阶滤波器串联时,总的传递函数 H ( s ) H(s) H(s) 为:
H ( s ) = H 1 ( s ) ⋅ H 2 ( s ) H(s) = H_1(s) \cdot H_2(s) H(s)=H1(s)⋅H2(s)
即:
H ( s ) = ( 1 1 + s / ω c 1 ) ⋅ ( 1 1 + s / ω c 2 ) H(s) = \left( \frac{1}{1 + s / \omega_{c1}} \right) \cdot \left( \frac{1}{1 + s / \omega_{c2}} \right) H(s)=(1+s/ωc11)⋅(1+s/ωc21)
假设两个一阶滤波器的截止频率相同,即 ω c 1 = ω c 2 = ω c \omega_{c1} = \omega_{c2} = \omega_c ωc1=ωc2=ωc,则总的传递函数为:
H ( s ) = ( 1 1 + s / ω c ) 2 H(s) = \left( \frac{1}{1 + s / \omega_c} \right)^2 H(s)=(1+s/ωc1)2
将其展开得到:
H ( s ) = 1 ( 1 + s / ω c ) 2 = 1 1 + 2 s ω c + ( s ω c ) 2 H(s) = \frac{1}{(1 + s / \omega_c)^2} = \frac{1}{1 + \frac{2s}{\omega_c} + \left( \frac{s}{\omega_c} \right)^2} H(s)=(1+s/ωc)21=1+ωc2s+(ωcs)21
这就是一个标准的二阶低通滤波器的传递函数形式。它可以表示为:
H ( s ) = 1 1 + 2 s ω c + ( s ω c ) 2 H(s) = \frac{1}{1 + \frac{2s}{\omega_c} + \left( \frac{s}{\omega_c} \right)^2} H(s)=1+ωc2s+(ωcs)21
或者更一般的形式:
H ( s ) = ω c 2 s 2 + 2 ζ ω c s + ω c 2 H(s) = \frac{\omega_c^2}{s^2 + 2\zeta\omega_c s + \omega_c^2} H(s)=s2+2ζωcs+ωc2ωc2
其中, ζ \zeta ζ 是阻尼系数,对于上述情况 ζ = 1 \zeta = 1 ζ=1。通过改变 ζ \zeta ζ 的值,可以设计出具有不同频率特性的二阶滤波器。
总结
通过将两个一阶低通滤波器串联,我们得到了一个二阶低通滤波器的传递函数。这个方法可以推广到高通、带通和带阻滤波器,通过适当的组合一阶滤波器可以实现各种复杂的频率响应特性。
相关文章:

[信号与系统]模拟域中的一阶低通滤波器和二阶滤波器
前言 不是学电子出身的,这里很多东西是问了朋友… 模拟域中的一阶低通滤波器传递函数 模拟域中的一阶低通滤波器的传递函数可以表示为: H ( s ) 1 s ω c H(s) \frac{1}{s \omega_c} H(s)sωc1 这是因为一阶低通滤波器的设计目标是允许低频信…...
Mac环境 aab包转apks,并安装apks
一、下载下载bundletool工具 Releases google/bundletool GitHub 二、将下载bundletool.jar包、aab、keystore文件全部放到同一个目录下 例如我全部放到download目录下 转换命令行: java -jar bundletool-all-1.16.0.jar build-apks --modeuniversal --bundle…...

银河麒麟V10 SP1.1操作系统 离线安装 nginx1.21.5、redis 服务
银河麒麟官网地址:国产操作系统、麒麟操作系统——麒麟软件官方网站 一、查看系统版本 命令:nkvers 我的是 release V10 (SP1),根据这个版本去官网找对应的rpm包 银河麒麟操作系统的rpm包必须从官方找, 要是随便找个Centos的rp…...
 格式的视频 H.264格式的可以播放)
ios swift5 视频播放 播放视频失败 无法播放HEVC (H.265) 格式的视频 H.264格式的可以播放
文章目录 1.问题2.原因:iOS swift AVPlayerViewController无法播放HEVC (H.265) 格式的视频3.解决方法用第三方框架MobileVLCKit来播放4.用MobileVLCKit写的播放器4.1 两个oc版本的4.2 两个swiftUI版本的5.苹果是支持HEVC (H.265) 格式的视频,是硬件那边…...

网工内推 | 网络工程师,IE认证优先,最高18k*14薪,周末双休
01 上海吾索信息科技有限公司 🔷招聘岗位:网络工程师 🔷岗位职责: 1)具备网络系统运维服务经验以及数据库实施经验,具备网络系统认证相关资质或证书; 2)掌握常用各设备的运维巡检…...
【Qt】QMessageBox 各种对话框的默认显示效果
1. 函数原型 void about(QWidget *parent, const QString &title, const QString &text)void aboutQt(QWidget *parent, const QString &title QString())QMessageBox::StandardButton critical(QWidget *parent, const QString &title, const QString &…...

一文弄懂线性回归模型
1、引言 今天,我们将深入探讨机器学习中的三个关键概念:线性回归、代价函数和梯度下降。这些概念构成了许多机器学习算法的基础。起初,我决定不写一篇关于这些主题的文章,因为它们已经被广泛涉及。不过,我改变了主意&…...

uniApp获取实时定位
通过你获取的key放到项目manifest.json里面,对应填写你所需要的key值,还有高德用户名 用户名: key值的位置: 代码: html: <view class"intList pdNone"><view class"label">详细地…...

linux的source命令
用法 source file 也可以用.空格file来代替 . file 作用 在当前bash环境下读取并执行FileName中的命令. source(或点)令通常用于重新执行刚修改的初始化文档,如 .bash_profile 和 .profile等配置文件. 简单的说就是: source命令会把file里的命令在当前shell里一…...
2024年理论考试题库。)
特种作业操作证(焊接与热切割作业)2024年理论考试题库。
1.关于隐弧排烟罩下列说法正确的是()。 A.这类排烟罩适用于焊接大而长的焊件时排除电焊烟尘和有毒气体 B.这类排烟罩对焊接区实行密闭,能最大限度地减少臭氧等有毒气体的弥散 C.利用压缩空气从主管中高速喷出时,在副管形成负压…...

免交互和嵌入执行模式
目录 概念 语法格式 统计行数 赋值变量 修改密码编辑往文件里添加内容 编辑编辑引入变量 整体赋值编辑 加引号不赋值变量 expect实现免交互 免交互设置密码 免交互切换用户 嵌入执行模式 添加用户并免交互设置密码 免交互登录 传参实现ssh 练习 概念 …...

Hadoop版本演变、分布式集群搭建
Hadoop版本演变历史 Hadoop发行版非常的多,有华为发行版、Intel发行版、Cloudera Hadoop(CDH)、Hortonworks Hadoop(HDP),这些发行版都是基于Apache Hadoop衍生出来的。 目前Hadoop经历了三个大的版本。 hadoop1.x:HDFSMapReduce hadoop2.x…...

【Qt C++实现绘制仪表盘】
要在Qt C中绘制仪表盘,您可以使用QChart、QSeries、QBarSeries、QPointSeries等类。以下是一个简单的示例,演示如何使用这些类创建一个绘图仪表盘: #include <QApplication> #include <QChart> #include <QChartView> #in…...

一文看懂LLaMA 2:大型多模态模型的新里程碑
一文看懂LLaMA 2:大型多模态模型的新里程碑 LLaMA 2是OpenAI继GPT-3之后推出的又一重磅模型,它不仅在文本生成方面有所突破,而且在图像处理和语音识别等领域也展现出了令人印象深刻的能力。本文将全面介绍LLaMA 2的背景、技术细节、应用场景…...

基于Spring Boot构建淘客返利平台
基于Spring Boot构建淘客返利平台 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将讨论如何基于Spring Boot构建一个淘客返利平台。 淘客返利平台通过…...
Qt—贪吃蛇项目(由0到1实现贪吃蛇项目)
用Qt实现一个贪吃蛇项目 一、项目介绍二、游戏大厅界面实现2.1完成游戏大厅的背景图。2.2创建一个按钮,给它设置样式,并且可以跳转到别的页面 三、难度选择界面实现四、 游戏界面实现五、在文件中写入历史战绩5.1 从文件里提取分数5.2 把贪吃蛇的长度存入…...

Java导出Excel并邮件发送
一、导出Excel 添加maven依赖 <dependency><groupId>org.apache.poi</groupId><artifactId>poi-ooxml</artifactId><version>3.10-FINAL</version></dependency><dependency><groupId>org.apache.poi</groupI…...
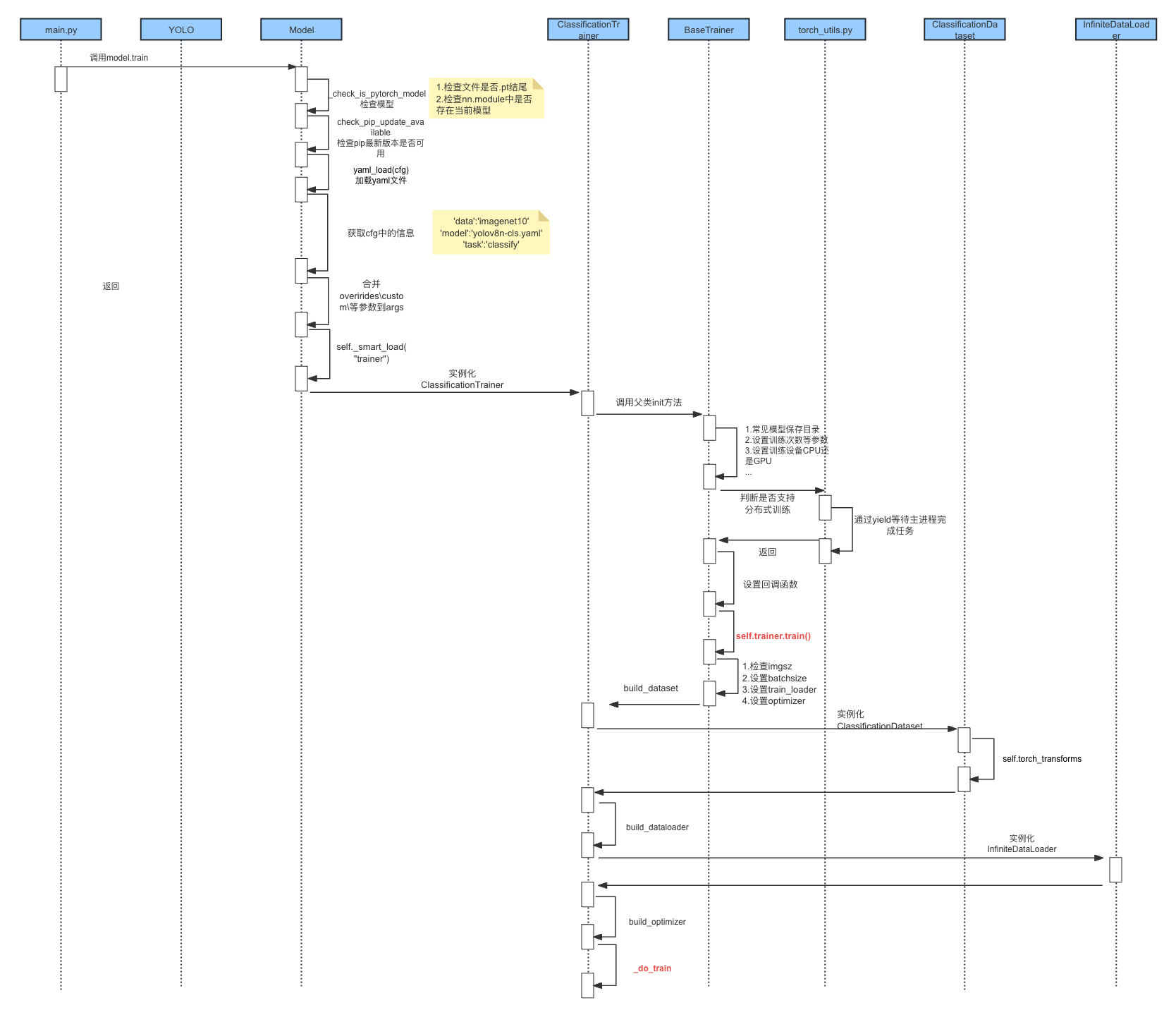
【课程总结】Day12:YOLO的深入了解
前言 在【课程总结】Day11(下):YOLO的入门使用一节中,我们已经了解YOLO的使用方法,使用过程非常简单,训练时只需要三行代码:引入YOLO,构建模型,训练模型;预测…...

保护隐私,释放智能:使用LangChain和Presidio构建安全的AI问答系统
保护隐私,释放智能:使用LangChain和Presidio构建安全的AI问答系统 在人工智能(AI)飞速发展的今天,AI问答系统已经成为企业与客户互动的重要工具。然而,随之而来的个人数据隐私问题也日益凸显。如何在不泄露…...

【高考志愿】自动化
目录 一、专业概述 二、课程设计 三、就业前景与方向 四、志愿填报 五、自动化专业排名 一、专业概述 高考志愿自动化专业选择,无疑是迈向现代化工业与科技发展的一把金钥匙。自动化专业,作为现代工程领域的重要支柱,融合了计算机、电子…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
