回溯法c++学习 解决八皇后问题
使用回溯法解决八皇后问题
八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8
的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。这个问题可以推广为更一般的n 皇后摆放问题,其中棋盘的大小变为n×n ,而皇后个数也变成n 。当且仅当n=1 或n≥4
时,问题有解
#include <iostream>
#include <vector>class Solution {
private:std::vector<std::vector<std::string>> results; // 存储所有有效的棋盘配置public:std::vector<std::vector<std::string>> solveNQueens(int n) {std::vector<std::string> board(n, std::string(n, '.')); // 初始化棋盘,全部填充为'.'backtrack(board, 0); // 从第0行开始回溯return results;}private:void backtrack(std::vector<std::string>& board, int row) {if (row == board.size()) { // 如果已经放置了n个皇后(到达最后一行之后),找到一个有效解results.push_back(board);return;}int n = board[row].size();for (int col = 0; col < n; col++) { // 尝试在当前行的每一列放置皇后if (isValid(board, row, col)) { // 检查在此位置放置皇后是否有效board[row][col] = 'Q'; // 放置皇后backtrack(board, row + 1); // 递归到下一行board[row][col] = '.'; // 回溯,撤销这个位置的皇后}}}bool isValid(const std::vector<std::string>& board, int row, int col) {int n = board.size();// 检查同一列for (int i = 0; i < row; i++) {if (board[i][col] == 'Q') return false;}// 检查左上对角线for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {if (board[i][j] == 'Q') return false;}// 检查右上对角线for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if (board[i][j] == 'Q') return false;}return true; // 如果通过所有检查,则此位置有效}
};int main() {Solution solution;auto results = solution.solveNQueens(8); // 解决8皇后问题// 打印所有解for (int i = 0; i < results.size(); i++) {std::cout << "Solution " << i + 1 << ":\n";for (const auto& row : results[i]) {std::cout << row << "\n";}std::cout << "\n";}std::cout << "Total solutions: " << results.size() << std::endl;return 0;
}这段代码的详细解释如下:
- 我们定义了一个
Solution类来封装解决方案。 results成员变量用于存储所有有效的棋盘配置。solveNQueens函数是主入口点,它初始化棋盘并开始回溯过程。backtrack函数实现了回溯算法:- 如果已经成功放置了n个皇后,我们就找到了一个有效解。
- 否则,我们尝试在当前行的每一列放置皇后。
- 如果某个位置有效,我们就放置皇后,然后递归到下一行。
- 在回溯时,我们撤销这个位置的皇后。
isValid函数检查在特定位置放置皇后是否有效:- 检查同一列是否已有皇后。
- 检查左上对角线是否已有皇后。
- 检查右上对角线是否已有皇后。
- 在
main函数中,我们创建Solution对象,解决8皇后问题,并打印所有解。
这个算法的时间复杂度是O(N!),其中N是棋盘的大小(在这里是8)。这是因为在最坏的情况下,我们需要尝试所有可能的排列。空间复杂度是O(N),主要用于递归调用栈和存储棋盘状态。
这个解决方案使用了回溯法,它通过系统地尝试所有可能的配置来找到所有有效的解。每当发现当前路径不可行时,它就回溯并尝试下一个可能的选择。
但是八皇后问题的最有效的算法是位运算法
#include <iostream>
using namespace std;// 位运算解决八皇后问题
void solveNQueens(int n) {long upperlim = (1 << n) - 1; // 初始化,upperlim 表示 n 个皇后的所有列都已放置好long Ans = 0; // 记录解的个数// 递归函数,寻找可以放置皇后的位置void test(long row, long ld, long rd) {if (row != upperlim) {// pos 表示当前行可以放置皇后的位置long pos = upperlim & (~(row | ld | rd));while (pos) {// 取出最右边的可以放皇后的位置long p = pos & (-pos);pos -= p; // 移除该位置并递归调用 test 过程// 更新限制条件long new_ld = (ld | p) << 1;long new_rd = (rd | p) >> 1;test(row | p, new_ld, new_rd);}} else {++Ans; // 找到一个解}}// 调用参数test(0, 0, 0);cout << "共有 " << Ans << " 种排列" << endl;
}int main() {int n = 8; // 八皇后问题solveNQueens(n);return 0;
}
这段代码使用了位运算来高效地解决八皇后问题。核心思想是用一个整数变量表示每一行中哪些位置已经被占用,然后通过位运算判断某个位置是否可以放置皇后。具体解释如下:
upperlim初始化为2n−1,表示 n 个皇后的所有列都已放置好。test函数是递归的,它寻找可以放置皇后的位置。参数row、ld和rd分别表示在纵列和两个对角线方向的限制条件下,这一行的哪些地方不能放。- 位于该行上的冲突位置用
row、ld和rd中的 1 来表示。将它们三个进行并操作,得到该行所有的禁位,取反后就得到所有可以放的位置(用pos表示)。 p = pos & (-pos)取出pos最右边的那个 1,表示该行的某个可以放子的位置。将它从pos中移除并递归调用test过程。- 注意递归调用时三个参数的变化,每个参数都加上了一个禁位,但两个对角线方向的禁位对下一行的影响需要平移一位。
- 最后,如果递归到某个时候发现
row = upperlim,说明 n 个皇后全放进去了,找到的解的个数加一。
相关文章:

回溯法c++学习 解决八皇后问题
使用回溯法解决八皇后问题 八皇后问题是一个以国际象棋为背景的问题:如何能够在88 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。这…...
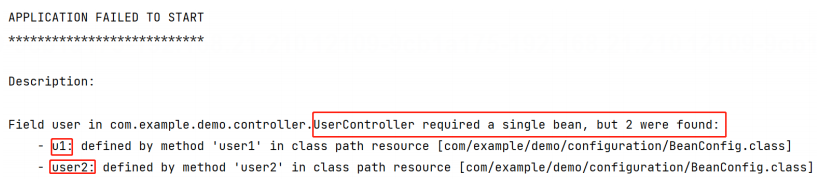
5. Spring IoCDI ★ ✔
5. Spring IoC&DI 1. IoC & DI ⼊⻔1.1 Spring 是什么?★ (Spring 是包含了众多⼯具⽅法的 IoC 容器)1.1.1 什么是容器?1.1.2 什么是 IoC?★ (IoC: Inversion of Control (控制反转))总…...
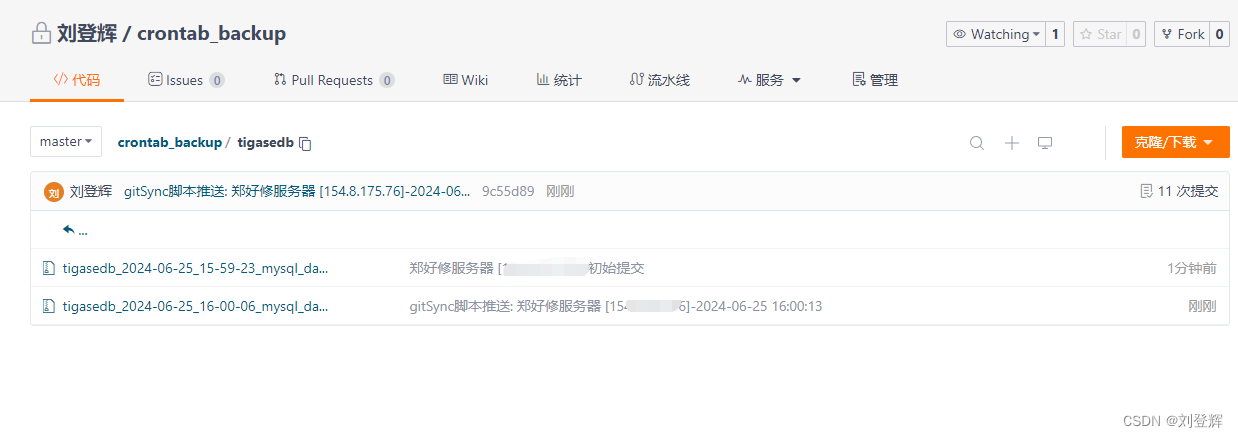
数据库自动备份到gitee上,实现数据自动化备份
本人有个不太好的习惯,每次项目的数据库都是在线上创建,Navicat 连接线上数据库进行处理,最近有一个项目需要二次升级,发现老项目部署的服务器到期了,完蛋,数据库咩了!!!…...

探索 Spring Cloud Gateway:构建微服务架构的关键一环
1. 简介 在当今的分布式系统中,微服务架构已经成为了一种流行的架构模式。在微服务架构中,服务被拆分为小型、可独立部署的服务单元,这些服务单元能够通过网络互相通信,形成一个整体的应用系统。然而,随着微服务数量的…...
P1114 “非常男女”计划最优解
原题地址 P1114 “非常男女”计划 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 代码题解 AC代码(1) 因为用的是级的算法,所以最后一个 了,这里使用特判来得到的,给你们放一下代码: #include <bi…...

C++ | Leetcode C++题解之第187题重复的DNA序列
题目: 题解: class Solution {const int L 10;unordered_map<char, int> bin {{A, 0}, {C, 1}, {G, 2}, {T, 3}}; public:vector<string> findRepeatedDnaSequences(string s) {vector<string> ans;int n s.length();if (n < L…...

构建、标记和发布镜像
构建、标记和发布镜像 目录 构建镜像标记镜像发布镜像实践 设置构建镜像推送镜像 在本指南中,您将学习以下内容: 构建镜像:基于Dockerfile构建镜像的过程。标记镜像:为镜像命名的过程,这也决定了镜像的分发位置。发…...
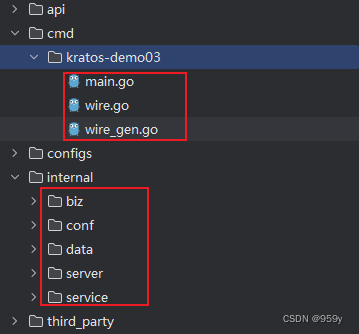
[Go Web] Kratos 使用的简单总结
文章目录 1.Kratos 简介2.传输协议3.日志4.错误处理5.配置管理6.wire 1.Kratos 简介 Kratos并不绑定于特定的基础设施,不限定于某种注册中心,或数据库ORM等,所以您可以十分轻松地将任意库集成进项目里,与Kratos共同运作。 API -&…...

首个实时 AI 视频生成技术发布;科大讯飞发布星火大模型 4.0 丨 RTE 开发者日报
开发者朋友们大家好: 这里是 「RTE 开发者日报」 ,每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE(Real-Time Engagement) 领域内「有话题的新闻」、「有态度的观点」、「有意思的数据」、「有思考的文章」、「…...

什么是容器镜像
什么是容器镜像? 1. 容器镜像的两个重要原则 容器镜像是容器化应用程序的基础,它包含了运行应用程序所需的一切——代码、运行时、库和依赖项。理解容器镜像的两个重要原则非常重要: 不可变性:容器镜像一旦构建,就不…...
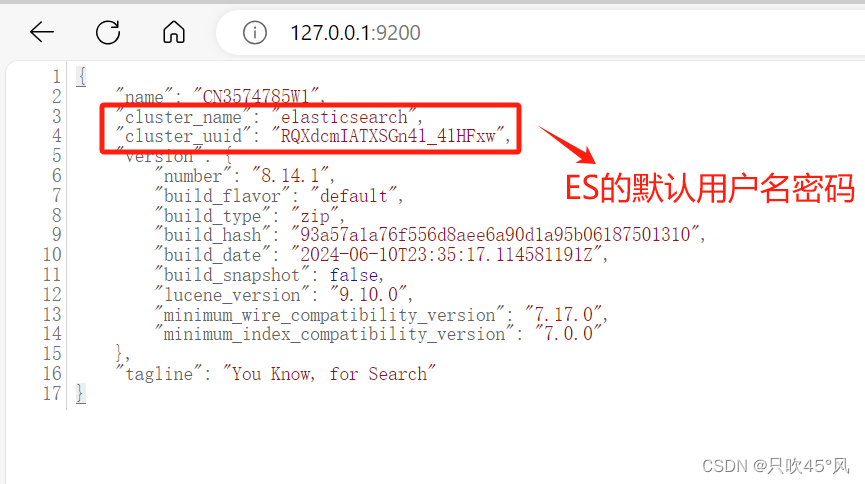
ElasticSearch-Windows系统ElasticSearch(ES)的下载及安装
前言 下载ElasticSearch 可以进入ElasticSearch官方下载地址,选择与电脑系统相对应的版本;博主已经上传资源,或者点此直接免费下载,本次演示版本为8.14.1。 注意: Elasticsearch 5 需要 Java 8 以上版本;…...

【应用开发二】GPIO操控(输出、输入、中断)
1 操控GPIO方式 控制目录:/sys/class/gpio /sys/class/gpio目录下文件如下图所示: 1.1 gpiochipX目录 功能:当前SoC所包含的所有GPIO控制器 i.mx6ull一共包含5个GPIO控制器,分别为GPIO1~5分别对应gpiochip0、gpiochip32、gpi…...

单点登录方法
一、父域cookie:两个有相同父域名的二级域名之间可以跨域传递cookie //注意该接口的地址也是baidu.com下属的二级域名:a.baidu.com //全部接口地址为:a.baidu.com/dev-api/system/ecdWeb/login。如果不是a.baidu.com那么根本带不过去 //其实可以理解为通过该方法将cookie传给…...

springboot集成JPA并配置hikariCP连接池问题解决
一、引入需要的依赖 springboot版本 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-parent</artifactId><version>2.3.2.RELEASE</version><relativePath/></parent> jpa依赖 <!--…...

vue2的双向绑定
vue是一个mvvm框架,即数据双向绑定,即当数据发生变化的时候,视图也就发生变化,当视图发生变化的时候,数据也会跟着同步变化。 Vue.js 2 中的双向绑定是通过 v-model 指令实现的。v-model 指令可以在表单输入元素上创建…...

Vue3 国际化i18n
国际化i18n方案 1. 什么是i18n2. i18n安装、配置及使用2.1 安装2.2 配置2.3 挂载到实例2.4 组件中使用2.5 语言切换 1. 什么是i18n i18n 是“国际化”的简称。在资讯领域,国际化(i18n)指让产品(出版物,软件,硬件等)无…...

算法金 | 使用随机森林获取特征重要性
大侠幸会幸会,我是日更万日 算法金;0 基础跨行转算法,国内外多个算法比赛 Top;放弃 BAT Offer,成功上岸 AI 研究院 Leader; <随机森林及其应用领域> 随机森林是一种强大的机器学习算法,其…...

网络安全的重要性
网络安全的重要性 网络安全是指保护网络系统免受未授权的访问、攻击、破坏或未经授权的数据泄露的能力。随着互联网的普及和数字化进程的加速,网络安全问题日益凸显,成为个人、企业和国家必须面对的重要挑战。 网络安全的威胁 网络安全威胁包括黑客攻…...

Leetcode40 无重复组合之和
题目描述: 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意:解集不能包含重复的组合。 思路分析 这个题是…...

详解MATLAB中处理日期和时间的函数
在MATLAB中处理日期和时间时,可以使用多种函数来进行计时和时间差计算。以下是对一些常用函数的详细解释: 1. tic 和 toc 用途:用来测量一段代码执行的时间。用法:tic; % 启动秒表 % 你的代码 elapsedTime toc; % 停止秒表&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

简约商务通用宣传年终总结12套PPT模版分享
IOS风格企业宣传PPT模版,年终工作总结PPT模版,简约精致扁平化商务通用动画PPT模版,素雅商务PPT模版 简约商务通用宣传年终总结12套PPT模版分享:商务通用年终总结类PPT模版https://pan.quark.cn/s/ece1e252d7df...
