Dijkstra算法C代码
一个带权图n个点m条边,求起点到终点的最短距离
先定义一个邻接矩阵graph,graph[i][j]表示从i到j的距离,i到j没有路就表示为无穷
然后定义一个visit数组,visit[i]表示i结点是否被访问
然后定义一个dist数组,dist[i]表示起点到i结点的最短距离
第一行输入n和m,表示有n个点m条边
接下来m行输入三个整数a,b,c,表示a到b存在一个距离为c的边
例如输入
4 4
0 1 500
0 2 100
1 3 200
1 2 300
图如下
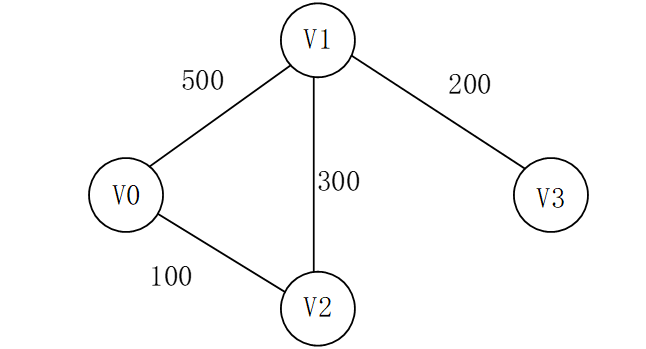
先初始化dist,初始值为起点到所有点的直达距离
dist={0,500,100,inf},inf表示无穷,即不能直达
一开始起点被访问,所以visit初始化为
visit={1,0,0,0}
将除起点和终点外的每个点都作为中心节点并更新最短路径
一开始dist数组中{0,500,100,inf}最小值为100,对应的点为v2,所以将v2作为中心节点,令mid=2,再计算v2到所有未访问点的直达距离,更新dist,此时还有v1和v3未访问
dist变为{0,400,100,inf}
然后令visit[mid]=1表示已访问,依次类推,经过n-1轮后每个点visit位都为1,这个时候dist数组中dist[i]就表示起点到i结点的最短路径
#include<stdio.h>
#define inf 99999; //定义99999为无穷大
int dist[10];
int visit[10];
int graph[10][10];
int main(){scanf("%d%d",&n,&m);//先初始化所有边为无穷 for(i=0;i<n;i++){for(j=0;j<n;j++)graph[i][j]=inf;}//根据输入修改graghfor(i=0;i<m;i++){scanf("%d%d%d",&a,&b,&c); //从a到b的距离为c graph[a][b]=c;graph[b][a]=c; //由于是无向图,所以反过来也是c graph[i][i]=0; //自己到自己距离为0}visit[0]=1; //起点访问初始化为0 for(i=0;i<n;i++)dist[i]=graph[0][i];for(i=1;i<n;i++){//n个点需要n-1轮循环,因为一开始起点已经初始化了 //找dist数组最小值并记录下标为mid min_dist=inf;mid=0; for(j=0;j<n;j++){if((visit[j]==0) && (dist[j]<min_dist)){min_dist=dist[j];mid=j;}}//以mid为中心节点更新dist for(k=0;k<n;k++){if((visit[k]==0) && (dist[k]>dist[mid]+graph[mid][k])){dist[k]=dist[mid]+graph[mid][k];}}visit[mid]=1;//更新完后标记mid为访问 }for(i=0;i<n;i++)printf("%d ",dist[i]); //输出起点到每个点的最短路径return 0;
}
相关文章:

Dijkstra算法C代码
一个带权图n个点m条边,求起点到终点的最短距离 先定义一个邻接矩阵graph,graph[i][j]表示从i到j的距离,i到j没有路就表示为无穷 然后定义一个visit数组,visit[i]表示i结点是否被访问 然后定义一个dist数组,dist[i]表…...

P1064 [NOIP2006 提高组] 金明的预算方案
[NOIP2006 提高组] 金明的预算方案 题目描述 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置࿰…...

大型企业组网如何规划网络
大型企业组网是一个复杂的过程,它需要细致的规划和设计,以确保网络能够满足企业的业务需求,同时保证性能、安全性和可扩展性。以下是规划大型企业网络的一些关键步骤和考虑因素: 1. 需求分析 业务需求:与各个业务部门…...
)
java:aocache的单实例缓存(二)
之前一篇博客《java:aocache的单实例缓存》介绍了aoocache使用注解AoCacheable实现单实例缓存的方式,同时也指出了这种方式的使用限制,就是这个注解定义的构造方法,不能再创建出新实例。 为了更灵活方便的实现单实例。aocache最新版本0.4.0增…...
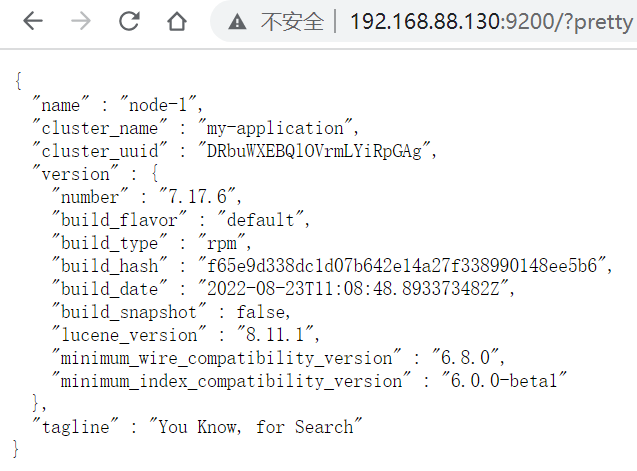
ElasticSearch安装部署
简介 Elasticsearch 是一个开源的分布式搜索和分析引擎,用于实时地存储、检索和分析大数据量。它基于 Apache Lucene 搜索引擎库构建而成,提供了一个强大、稳定且易于扩展的搜索解决方案。 主要特点和用途: 分布式存储和搜索: E…...
——开发:数据转换——影响因素、直接作用、主要特征)
数据赋能(132)——开发:数据转换——影响因素、直接作用、主要特征
影响因素 数据转换过程中需要考虑的一些影响因素: 数据格式与结构: 不同系统或应用可能使用不同的数据格式(如JSON、XML、CSV等)和数据结构(如关系型数据库、非关系型数据库等)。数据转换需要确保原始数据…...

TMGM:ASIC撤销禁令,TMGM强化合规、重启差价合约服务
TMGM作为差价合约(CFDs)与保证金外汇交易领域的领航者,安全、合规、高效被奉为我集团的终身使命。澳大利亚证券和投资委员会(ASIC)已正式撤销了早前针对TMGM差价合约业务实施的临时止损令。这一误会的解除,…...

基于SpringBoot网吧管理系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 Java精品实战案例《600套》 2025-2026年最值得选择的Java毕业设计选题大全࿱…...
实测2024年最佳的三款Socks5代理IP网站
一、引言 在浩瀚的网络世界中,Socks5代理IP服务如同导航灯塔,指引我们穿越数据海洋,安全、稳定地访问目标网站。作为专业的测评团队,我们深知一款优秀的Socks5代理IP网站需要具备哪些特质:稳定的IP资源、高效的连接速…...
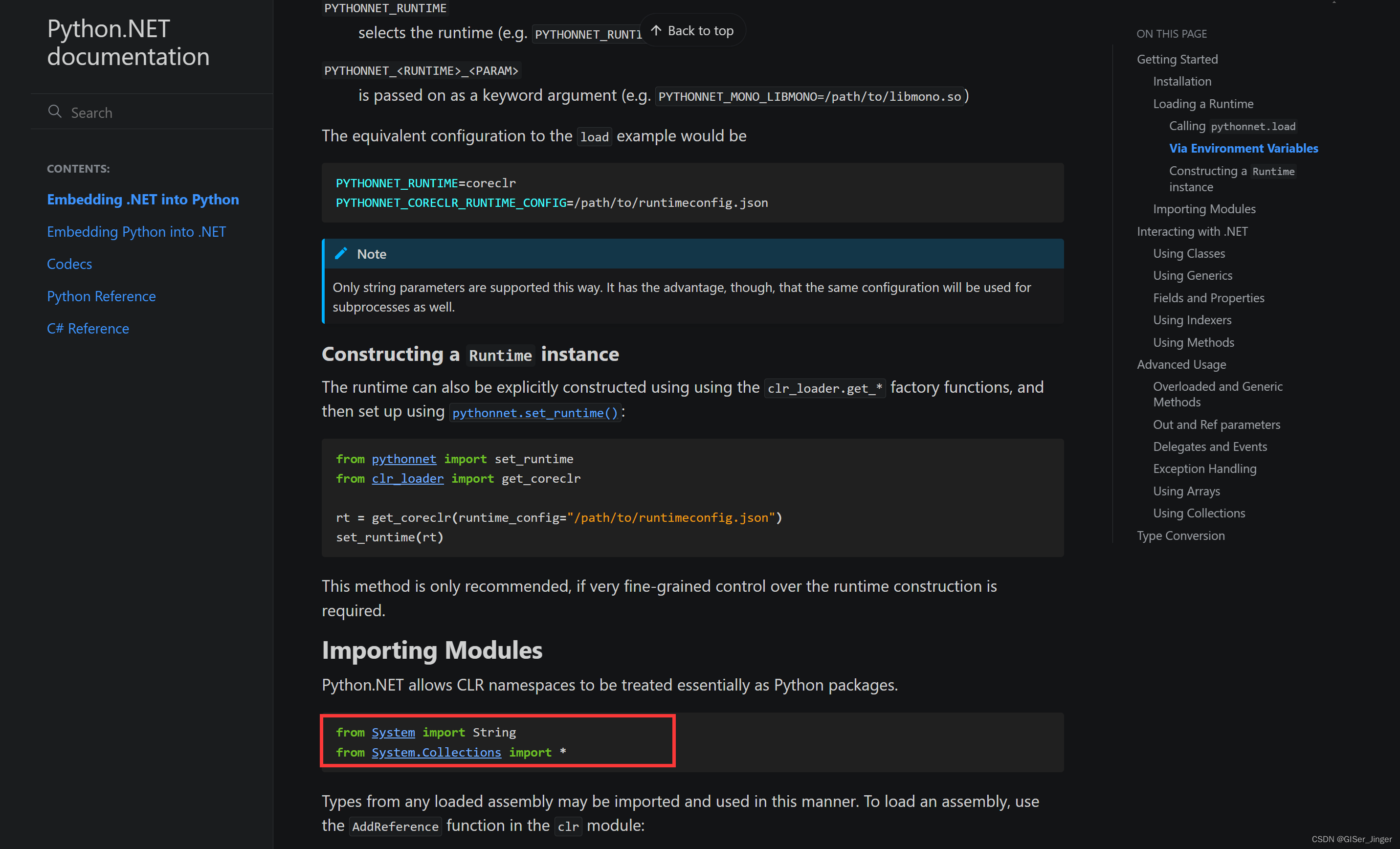
Pythonnet能导入clr,但无法引入System模块?
【pythonnet详解】—— Python 和 .NET 互操作的库_pythonnet 详细使用-CSDN博客 Python中动态调用C#的dll动态链接库中方法_python 如何调用c# dll-CSDN博客 需求:Python调用并传List<float>类型参数给.Net 起初:直接 # 创建一个Python浮点数…...

媒体宣发套餐的概述及推广方法-华媒舍
在今天的数字化时代,对于产品和服务的宣传已经变得不可或缺。媒体宣发套餐作为一种高效的宣传方式,在帮助企业塑造品牌形象、扩大影响力方面扮演着重要角色。本文将揭秘媒体宣发套餐,为您呈现一条通往成功的路。 1. 媒体宣发套餐的概述 媒体…...
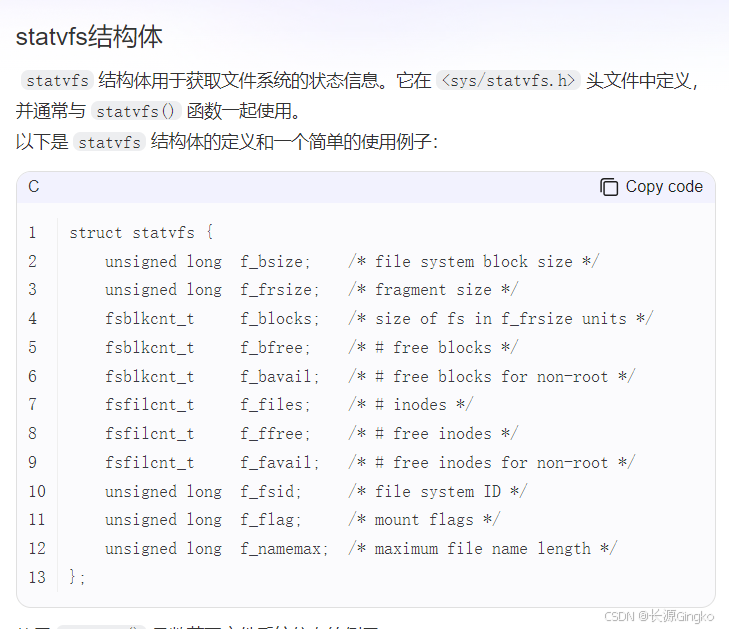
Windows和Linux C++判断磁盘空间是否充足
基本是由百度Ai写代码生成的,记录一下。实现此功能需要调用系统的API函数。 对于Windows,可调用函数GetDiskFreeSpaceEx,使用该函数需要包含头文件windows.h。该函数的原型: 它的四个参数: lpDirectoryName࿰…...

数据访问层如何提取数据到其他层,其他类中
当然可以,以下是一些具体的例子,展示了如何将数据库访问逻辑封装在一个单独的类中,并在其他类中使用这个类来获取数据。 数据库访问类(DatabaseAccess.java): java复制代码 import java.sql.*; import ja…...

【JS】AI总结:JavaScript中常用的判空方法
在JavaScript中,判空是一个常见的操作,因为变量可能未定义、未初始化或包含特定的空值。以下是JavaScript中常用的判空方法: 使用if语句直接判断: 如果变量是null、undefined、0、NaN、空字符串(""ÿ…...
Rust单元测试、集成测试
单元测试、集成测试 在了解了如何在 Rust 中写测试用例后,本章节我们将学习如何实现单元测试、集成测试,其实它们用到的技术还是上一章节中的测试技术,只不过对如何组织测试代码提出了新的要求。 单元测试 单元测试目标是测试某一个代码单…...
vue全局方法plugins/utils
一、在src目录下创建一个plugins文件夹 test.ts文件存放创建的方法,index.ts用于接收所有自定义方法进行统一处理 二、编写自定义方法 // test.ts文件 export default {handleTest(val1: number, val2: number) {// 只是一个求和的方法return val1 val2;}, };三…...

高阶算法班从入门到精通之路
课程介绍 本课程旨在帮助学员深入理解算法与数据结构的核心概念,从而掌握高级算法设计与分析技能。每集课程内容精心设计,涵盖了常用数据结构、经典算法及其应用场景等方面的深度讲解,同时通过大量实例演练,帮助学员提升解决实际…...

C++ 左值右值
文章目录 概述左值右值右值引用左值和右值的互换 小结 概述 左值和右值属于2中不同的表达式类型;它们在表达式中扮演不同的角色,特别是在赋值操作和函数参数传递中。 左值 定义:左值是指那些在内存中有确定位置的表达式,可以出…...
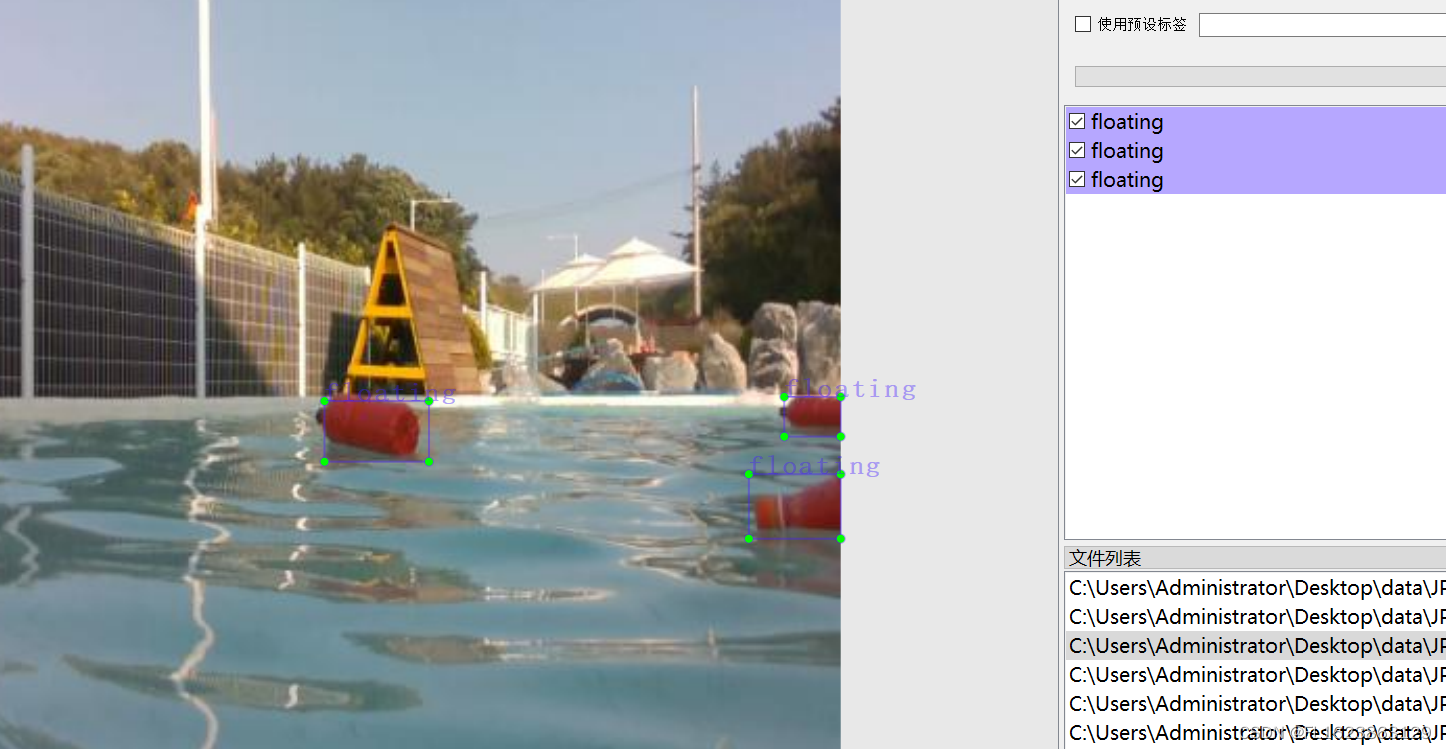
[数据集][目标检测]水面垃圾水面漂浮物检测数据集VOC+YOLO格式3749张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):3749 标注数量(xml文件个数):3749 标注数量(txt文件个数):3749 标注…...
[深度学习] 卷积神经网络CNN
卷积神经网络(Convolutional Neural Network, CNN)是一种专门用于处理数据具有类似网格结构的神经网络,最常用于图像数据处理。 一、CNN的详细过程: 1. 输入层 输入层接收原始数据,例如一张图像,它可以被…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
