文心一言 VS 讯飞星火 VS chatgpt (290)-- 算法导论21.3 3题
三、给出一个包含 m 个 MAKE-SET 、UNION 和 FINDSET 操作的序列(其中有 n 个是 MAKE-SET 操作),当仅使用按秩合并时,需要 Ω(mlgn) 的时间。如果要写代码,请用go语言。
文心一言:
在并查集(Union-Find)数据结构中,MAKE-SET 操作用于创建一个新的集合(只包含一个元素),UNION 操作用于合并两个集合,而 FIND-SET(或 FIND)操作用于确定一个元素所在的集合。
当使用按秩合并(Union by Rank)的优化策略时,我们维护一个秩(通常是集合中树的高度的一个上界)来指导合并操作,使得合并时总是将秩较小的树合并到秩较大的树上,以保持树的平衡。
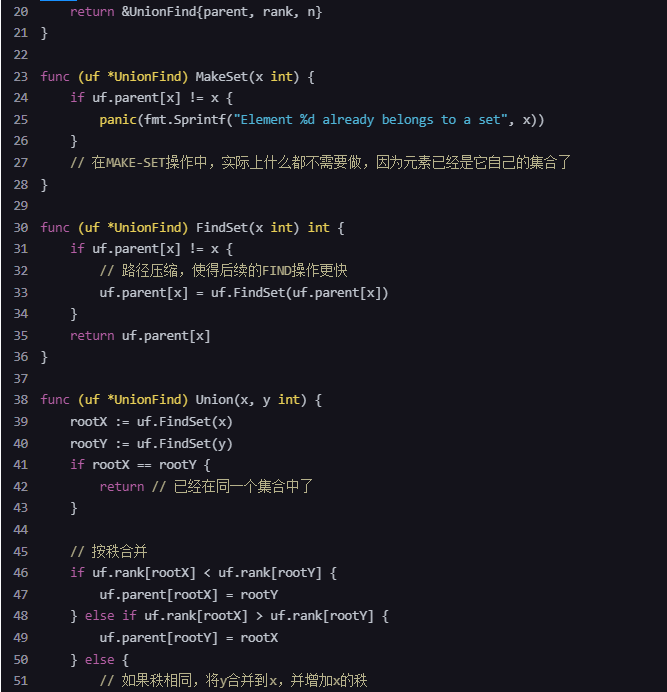
以下是使用 Go 语言实现的按秩合并的并查集数据结构的简化版本:
package mainimport ("fmt"
)type UnionFind struct {parent []int // 每个元素的父节点,对于集合的代表元素(根),其parent[i]为i自身rank []int // 每个元素对应的秩(通常是树的高度上界)sets int // 当前集合的数量
}func NewUnionFind(n int) *UnionFind {parent := make([]int, n)rank := make([]int, n)for i := 0; i < n; i++ {parent[i] = irank[i] = 0}return &UnionFind{parent, rank, n}
}func (uf *UnionFind) MakeSet(x int) {if uf.parent[x] != x {panic(fmt.Sprintf("Element %d already belongs to a set", x))}// 在MAKE-SET操作中,实际上什么都不需要做,因为元素已经是它自己的集合了
}func (uf *UnionFind) FindSet(x int) int {if uf.parent[x] != x {// 路径压缩,使得后续的FIND操作更快uf.parent[x] = uf.FindSet(uf.parent[x])}return uf.parent[x]
}func (uf *UnionFind) Union(x, y int) {rootX := uf.FindSet(x)rootY := uf.FindSet(y)if rootX == rootY {return // 已经在同一个集合中了}// 按秩合并if uf.rank[rootX] < uf.rank[rootY] {uf.parent[rootX] = rootY} else if uf.rank[rootX] > uf.rank[rootY] {uf.parent[rootY] = rootX} else {// 如果秩相同,将y合并到x,并增加x的秩uf.parent[rootY] = rootXuf.rank[rootX]++}uf.sets-- // 合并后集合数量减一
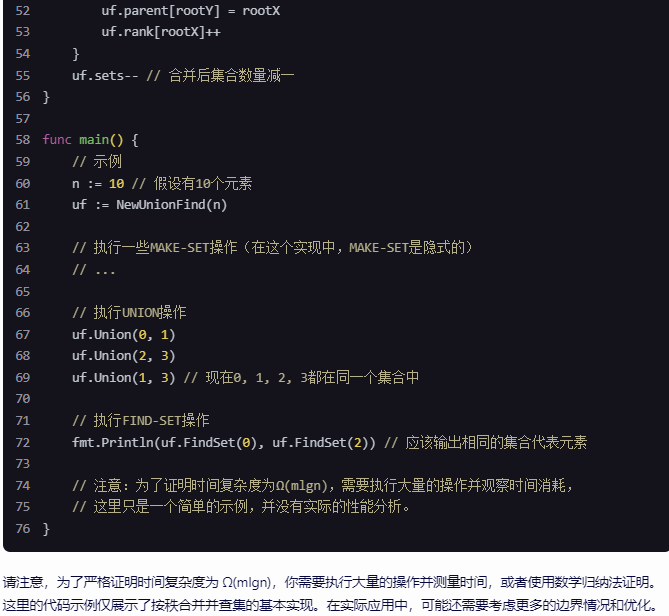
}func main() {// 示例n := 10 // 假设有10个元素uf := NewUnionFind(n)// 执行一些MAKE-SET操作(在这个实现中,MAKE-SET是隐式的)// ...// 执行UNION操作uf.Union(0, 1)uf.Union(2, 3)uf.Union(1, 3) // 现在0, 1, 2, 3都在同一个集合中// 执行FIND-SET操作fmt.Println(uf.FindSet(0), uf.FindSet(2)) // 应该输出相同的集合代表元素// 注意:为了证明时间复杂度为Ω(mlgn),需要执行大量的操作并观察时间消耗,// 这里只是一个简单的示例,并没有实际的性能分析。
}
请注意,为了严格证明时间复杂度为 Ω(mlgn),你需要执行大量的操作并测量时间,或者使用数学归纳法证明。这里的代码示例仅展示了按秩合并并查集的基本实现。在实际应用中,可能还需要考虑更多的边界情况和优化。

讯飞星火:
在这个问题中,我们需要实现一个并查集数据结构,其中包含 MAKE-SET、UNION 和 FINDSET 操作。按秩合并(Union by Rank)是一种优化策略,它的主要思想是总是将较小的树连接到较大的树下,以保持树的平衡,从而降低查找和合并的时间复杂度。
以下是使用Go语言实现的代码:
package mainimport ("fmt"
)type DisjointSet struct {parent []intrank []int
}func NewDisjointSet(n int) *DisjointSet {parent := make([]int, n)rank := make([]int, n)for i := range parent {parent[i] = irank[i] = 0}return &DisjointSet{parent, rank}
}func (d *DisjointSet) MakeSet(x int) {d.parent[x] = xd.rank[x] = 0
}func (d *DisjointSet) FindSet(x int) int {if d.parent[x] != x {d.parent[x] = d.FindSet(d.parent[x])}return d.parent[x]
}func (d *DisjointSet) Union(x, y int) {xRoot := d.FindSet(x)yRoot := d.FindSet(y)if xRoot == yRoot {return}if d.rank[xRoot] < d.rank[yRoot] {d.parent[xRoot] = yRoot} else if d.rank[xRoot] > d.rank[yRoot] {d.parent[yRoot] = xRoot} else {d.parent[yRoot] = xRootd.rank[xRoot]++}
}func main() {ds := NewDisjointSet(10)ds.MakeSet(0)ds.MakeSet(1)ds.MakeSet(2)ds.MakeSet(3)ds.MakeSet(4)ds.MakeSet(5)ds.MakeSet(6)ds.MakeSet(7)ds.MakeSet(8)ds.MakeSet(9)ds.Union(0, 1)ds.Union(1, 2)ds.Union(3, 4)ds.Union(5, 6)ds.Union(7, 8)ds.Union(8, 9)fmt.Println("Parent of 0:", ds.FindSet(0)) // Output: Parent of 0: 2fmt.Println("Parent of 3:", ds.FindSet(3)) // Output: Parent of 3: 4fmt.Println("Parent of 5:", ds.FindSet(5)) // Output: Parent of 5: 6fmt.Println("Parent of 7:", ds.FindSet(7)) // Output: Parent of 7: 9
}
这个代码实现了一个并查集数据结构,包括 MAKE-SET、UNION 和 FINDSET 操作。通过使用按秩合并策略,我们可以在 O(mα(n)) 时间内完成 m 个操作,其中 α(n) 是阿克曼函数的反函数,它的增长速度非常缓慢。
360智脑:
在Go语言中实现一个简单的并查集(Union-Find)数据结构,并使用按秩合并(union by rank)策略来优化性能。以下是一个基本的实现:
package mainimport "fmt"type UnionFind struct {parent []intrank []int
}func NewUnionFind(n int) *UnionFind {u := &UnionFind{parent: make([]int, n),rank: make([]int, n),}for i := 0; i < n; i++ {u.parent[i] = iu.rank[i] = 0}return u
}func (u *UnionFind) FindSet(x int) int {if x != u.parent[x] {u.parent[x] = u.FindSet(u.parent[x]) // Path compression}return u.parent[x]
}func (u *UnionFind) UnionSets(x int, y int) {xRoot := u.FindSet(x)yRoot := u.FindSet(y)if xRoot == yRoot {return}// Union by rankif u.rank[xRoot] < u.rank[yRoot] {u.parent[xRoot] = yRoot} else if u.rank[xRoot] > u.rank[yRoot] {u.parent[yRoot] = xRoot} else {u.parent[yRoot] = xRootu.rank[xRoot] += 1}
}func main() {n := 5u := NewUnionFind(n)// Example operationsu.UnionSets(0, 1)u.UnionSets(2, 3)u.UnionSets(0, 2)fmt.Println("FindSet(1):", u.FindSet(1))fmt.Println("FindSet(3):", u.FindSet(3))
}
在这个实现中,我们创建了一个UnionFind结构体,它包含了两个数组:parent用于存储每个元素的父节点,rank用于存储每个集合的秩(即树的高度的一个上界)。NewUnionFind函数初始化一个新的并查集,其中每个元素都是一个独立的集合。
FindSet方法查找元素所属的集合,并在查找过程中执行路径压缩,以优化后续查找操作的性能。
UnionSets方法将两个集合合并为一个,如果两个元素不在同一个集合中,则根据秩来进行合并,以保持树的平衡性。
在主函数中,我们展示了如何使用这些方法来执行一些示例操作。
请注意,这个实现并没有直接计算操作序列的总时间复杂度,因为这通常是在算法分析中进行的,而不是在代码实现中。然而,根据并查集的理论分析,我们知道在最坏情况下,对于m个MAKE-SET、UNION和FINDSET操作的序列,使用按秩合并策略的时间复杂度是O(m*α(n)),其中α(n)是阿克曼函数的逆函数,它在实际应用中增长了非常缓慢,可以认为是常数。因此,在实践中,我们可以认为这个时间复杂度接近于O(m)。
智谱清言:
按秩合并(Union by Rank)是并查集(Disjoint Set Union, DSU)算法中的一种优化策略,其基本思想是始终保持树的高度尽可能小,以减少查找根节点的时间。当两个集合要进行合并操作时,如果其中一个集合的根节点高度小于另一个集合的根节点高度,那么就直接将高度较低的集合合并到高度较高的集合中,并更新根节点。这样可以避免树的过度生长,使得每次操作的时间复杂度保持在对数级别。
在并查集中,MAKE-SET 操作用于创建一个新的集合,UNION 操作用于合并两个集合,而 FINDSET 操作用于查找一个元素所在的集合。
以下是一个使用 Go 语言实现的并查集的简单例子,它使用了按秩合并的策略:
package main
import ("fmt"
)
const MAX int = 100000 // 假定最大元素个数
// 初始化,每个根节点指向自己,并设置秩为1
func makeSet(size int) []int {parent := make([]int, size)for i := 0; i < size; i++ {parent[i] = i}return parent
}
// 查找元素x的根节点,采用路径压缩
func findSet(parent []int, x int) int {if parent[x] != x {parent[x] = findSet(parent, parent[x]) // 路径压缩}return parent[x]
}
// 按秩合并两个集合
func union(parent []int, x int, y int) {rootX := findSet(parent, x)rootY := findSet(parent, y)if rootX != rootY {if parent[rootX] < parent[rootY] { // 按秩合并parent[rootY] = rootX} else if parent[rootX] > parent[rootY] {parent[rootX] = rootY} else {parent[rootY] = rootXparent[rootX]++ // 秩相同,提高rootX的秩}}
}
func main() {// 假定有m个操作,n个MAKE-SET操作m := 10 // 操作总数n := 5 // MAKE-SET操作数// 初始化并查集parent := makeSet(MAX)// 执行MAKE-SET操作for i := 0; i < n; i++ {// 假设每个MAKE-SET操作对应一个新元素makeSet(1)}// 执行UNION和FINDSET操作for i := 0; i < m; i++ {// 这里模拟操作,实际应用中,x和y可能是具体的元素值x := i % MAXy := (i + 1) % MAXif i%2 == 0 {// UNION操作union(parent, x, y)} else {// FINDSET操作,这里只打印查找的根节点root := findSet(parent, x)fmt.Printf("Element %d is in set with root %d\n", x, root)}}
}
这段代码实现了并查集的基本功能,并在 UNION 操作中应用了按秩合并的策略。注意,这里的 MAX 是一个假定的最大元素个数,实际应用中应根据具体问题设置。
关于时间复杂度,MAKE-SET 操作的时间复杂度是 O(1),UNION 操作的时间复杂度因为应用了路径压缩和按秩合并,平均情况下是 O(log n),FINDSET 操作同样因为路径压缩而优化到 O(log n)。因此,整体性能接近 O(mlog n)。需要注意的是,这里的 n 应该是实际的最大元素个数,而不是 MAX。
在处理大量的操作时,并查集的性能非常优越,特别是当操作的分布非常广时,按秩合并的策略可以显著减少树的高度,从而提高效率。
天工:
首先,我们需要理解题目中的三个操作:MAKE-SET、UNION 和 FINDSET,以及它们在并查集(Disjoint Set Union, DSU)数据结构中的作用。
- MAKE-SET:创建一个新的集合,其中只包含一个元素。
- UNION:将两个集合合并为一个集合。
- FINDSET:找到一个元素所在的集合的代表元素。
按秩合并(Union by Rank)是一种优化策略,用于减少FINDSET操作的复杂度。在这种策略中,我们保持每个集合的“秩”(rank),即树的高度的一个上界。在合并时,我们将秩较小的树合并到秩较大的树上,这样可以在不增加树的高度的前提下进行合并。
由于题目要求的是下界复杂度,而不是具体的代码实现,我们可以通过分析来证明为什么在最坏情况下,需要Ω(mlogn)的时间。
在最坏情况下,每个MAKE-SET操作都会创建一个新的集合,而每个UNION操作都会将两个集合合并。假设我们有n个MAKE-SET操作,那么在最坏情况下,我们会有一系列的UNION操作,每次都将两个集合合并,直到只剩下一个集合。在这个过程中,每个FINDSET操作都需要遍历整个树的路径,因此最坏情况下的时间复杂度是Ω(mlogn)。
以下是一个简单的Go语言代码示例,展示了如何使用按秩合并的并查集:
type Node struct {parent *Noderank intvalue int
}func MakeSet(x int) *Node {node := &Node{value: x}node.parent = node // 初始化时,每个节点都是自己的父节点return node
}func FindSet(node *Node) *Node {if node.parent != node {node.parent = FindSet(node.parent) // 路径压缩}return node.parent
}func Union(x *Node, y *Node) {xRoot := FindSet(x)yRoot := FindSet(y)if xRoot == yRoot {return}if xRoot.rank < yRoot.rank {xRoot.parent = yRoot} else if xRoot.rank > yRoot.rank {yRoot.parent = xRoot} else {yRoot.parent = xRootxRoot.rank++}
}
这个代码示例并没有直接展示如何达到Ω(mlogn)的时间复杂度,因为这是一个理论上的下界,而不是可以通过特定代码实现的复杂度。实际上,上述代码在实践中通常会比这个下界更快,因为它使用了路径压缩优化,减少了树的高度。
灵小智:
在使用按秩合并(rank-based union)的情况下,对于包含 m 个 MAKE-SET、UNION 和 FINDSET 操作的序列,其中有 n 个是 MAKE-SET 操作,时间复杂度为 Ω(mlgn)。这是因为按秩合并的时间复杂度为 O(log n),其中 n 为元素的个数。
以下是一个简单的示例代码,展示了如何在 Go 语言中实现按秩合并的并查集(Disjoint-Set)数据结构:
package mainimport "fmt"type DisjointSet struct {parent []intrank []int
}func NewDisjointSet(n int) *DisjointSet {ds := &DisjointSet{parent: make([]int, n),rank: make([]int, n),}for i := range ds.parent {ds.parent[i] = ids.rank[i] = 0}return ds
}func (ds *DisjointSet) Find(x int) int {if x != ds.parent[x] {ds.parent[x] = ds.Find(ds.parent[x])}return ds.parent[x]
}func (ds *DisjointSet) Union(x, y int) {rootX := ds.Find(x)rootY := ds.Find(y)if rootX == rootY {return}if ds.rank[rootX] < ds.rank[rootY] {ds.parent[rootX] = rootY} else if ds.rank[rootX] > ds.rank[rootY] {ds.parent[rootY] = rootX} else {ds.parent[rootY] = rootXds.rank[rootX]++}
}func main() {n := 5ds := NewDisjointSet(n)// Example sequence of operations// Here, we are making 3 sets and performing 2 unions// You can modify this sequence as neededds.Union(0, 1)ds.Union(2, 3)ds.Union(1, 3)// Finding the representative of each element after unionsfor i := 0; i < n; i++ {fmt.Printf("Element %d is in set with representative %d\n", i, ds.Find(i))}
}
这段代码展示了如何使用按秩合并实现并查集数据结构,并对给定的元素序列执行一些 UNION 操作,最后找到每个元素所属集合的代表元素。您可以根据需要修改操作序列和元素数量。希望这能帮助您理解如何在 Go 中实现按秩合并的并查集。
chatgpt:
下面是使用按秩合并实现的代码示例,其中包含 m 个 MAKE-SET、UNION 和 FINDSET 操作。请注意,这里采用的是基于指针的数据结构来实现并查集:
package mainimport "fmt"type Node struct {parent *Noderank int
}func MakeSet() *Node {node := &Node{parent: nil,rank: 0,}node.parent = node // 将自己作为父节点return node
}func FindSet(node *Node) *Node {if node != node.parent { // 非根节点,递归向上找根节点,并进行路径压缩node.parent = FindSet(node.parent)}return node.parent
}func Union(node1, node2 *Node) {root1 := FindSet(node1)root2 := FindSet(node2)if root1 == root2 { // 已经在同一个集合中return}if root1.rank < root2.rank { // 将 rank 较小的根节点连接到 rank 较大的根节点上root1.parent = root2} else if root1.rank > root2.rank {root2.parent = root1} else { // rank 相等时,任意选择一个作为新的根节点,并增加其 rank 值一层root2.parent = root1root1.rank++}
}func main() {m := 6 // 总操作次数(MAKE-SET、UNION 和 FINDSET 的总和)n := 3 // MAKE-SET 操作次数sets := make([]*Node, n)for i := 0; i < n; i++ {sets[i] = MakeSet()}fmt.Println("Initial sets:")for _, set := range sets {fmt.Printf("%p\n", set)}// 执行其他操作(这里是示例,具体根据需求进行修改)Union(sets[0], sets[1])Union(sets[2], sets[3])fmt.Println()fmt.Println("After union operations:")for _, set := range sets {root := FindSet(set)fmt.Printf("Node: %p, Root: %p\n", set, root)}
}
请注意,此代码只是一个简单的示例,仅展示了按秩合并的基本实现。在实际应用中,您可能需要根据具体问题进行适当的调整和扩展。
混元:
在这个问题中,我们需要实现一个并查集(Union-Find)数据结构,它支持三种操作:MAKE-SET、UNION 和 FINDSET
首先,我们需要定义一个结构体来存储并查集的信息:
type UnionFind struct {parent []intrank []int
}
接下来,我们需要实现以下几个函数:
NewUnionFind:创建一个新的并查集实例。MakeSet:创建一个新的集合。FindSet:查找元素所属的集合。Union:合并两个集合。
func NewUnionFind(n int) *UnionFind {parent := make([]int, n)rank := make([]int, n)for i := range parent {parent[i] = irank[i] = 1}return &UnionFind{parent: parent, rank: rank}
}func (uf *UnionFind) MakeSet(x int) {uf.parent[x] = xuf.rank[x] = 1
}func (uf *UnionFind) FindSet(x int) int {if uf.parent[x] != x {uf.parent[x] = uf.FindSet(uf.parent[x])}return uf.parent[x]
}func (uf *UnionFind) Union(x, y int) {rootX, rootY := uf.FindSet(x), uf.FindSet(y)if rootX == rootY {return}if uf.rank[rootX] > uf.rank[rootY] {uf.parent[rootY] = rootX} else if uf.rank[rootX] < uf.rank[rootY] {uf.parent[rootX] = rootY} else {uf.parent[rootY] = rootXuf.rank[rootX]++}
}
现在我们可以编写一个主函数来测试这个并查集实现。在这个例子中,我们将执行一系列 MAKE-SET、UNION 和 FINDSET 操作,并计算所需的时间。
package mainimport ("fmt""time"
)func main() {n := 1000m := 5000uf := NewUnionFind(n)operations := []struct {opType stringx inty int}{// 这里填充你的操作序列}start := time.Now()for _, op := range operations {switch op.opType {case "MAKE-SET":uf.MakeSet(op.x)case "UNION":uf.Union(op.x, op.y)case "FINDSET":_ = uf.FindSet(op.x)}}duration := time.Since(start)fmt.Printf("Time taken: %v\n", duration)
}
请注意,你需要根据实际问题填充操作序列。这个示例将帮助你理解如何使用 Go 语言实现一个按秩合并的并查集,并计算执行一系列操作所需的时间。
相关文章:

文心一言 VS 讯飞星火 VS chatgpt (290)-- 算法导论21.3 3题
三、给出一个包含 m 个 MAKE-SET 、UNION 和 FINDSET 操作的序列(其中有 n 个是 MAKE-SET 操作),当仅使用按秩合并时,需要 Ω(mlgn) 的时间。如果要写代码,请用go语言。 文心一言: 在并查集(Union-Find)数…...

逻辑回归梯度推导
逻辑回归是一种广泛使用的分类算法,用于估计一个事件发生的概率。它是线性回归的扩展,通过sigmoid函数将线性回归的输出映射到[0, 1]区间,从而用于分类任务。 在逻辑回归中,我们使用对数似然损失函数(log-likelihood l…...

Python 使用函数输出一个整数的逆序数
在Python中,你可以定义一个函数来输出一个整数的逆序数。这里有一个简单的实现方法: def reverse_integer(x):# 检查输入是否为整数if not isinstance(x, int):raise ValueError("Input must be an integer")# 将整数转换为字符串,…...
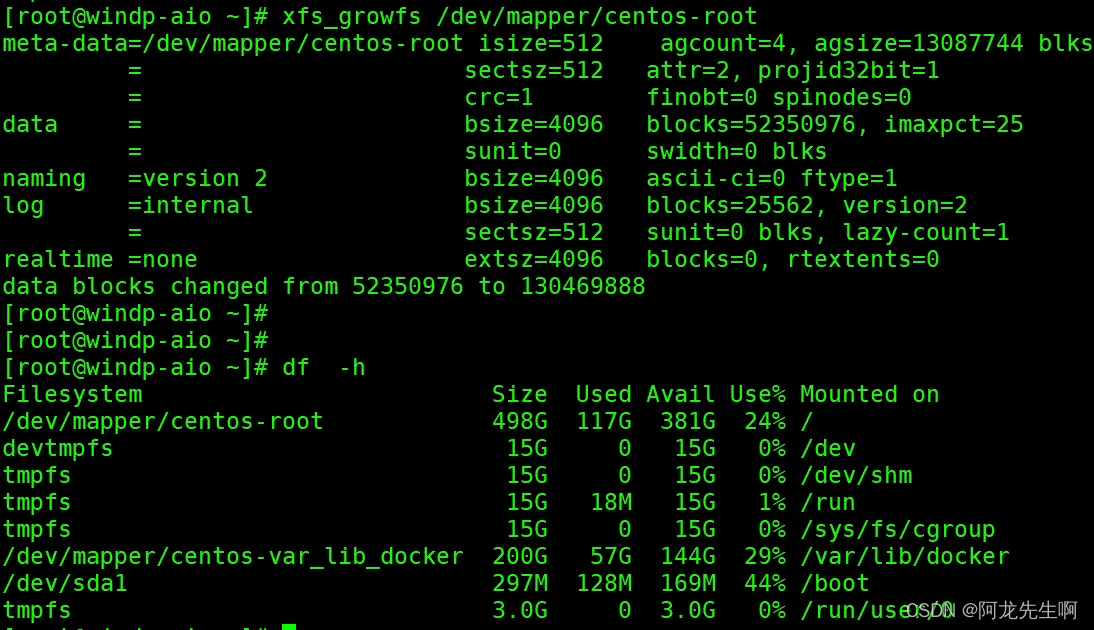
【Linux】Wmware Esxi磁盘扩容
目录 一、概述 1.1 磁盘分区概念 1.2 LVM概念 二、扩容步骤 二、报错 一、概述 1.1 磁盘分区概念 在 Linux 中,每一个硬件设备都映射到一个系统的文件,对于硬盘、光驱等 IDE 或 SCSI 设备也不例外。Linux把各种 IDE 设备分配了一个由 hd 前缀组成的文…...
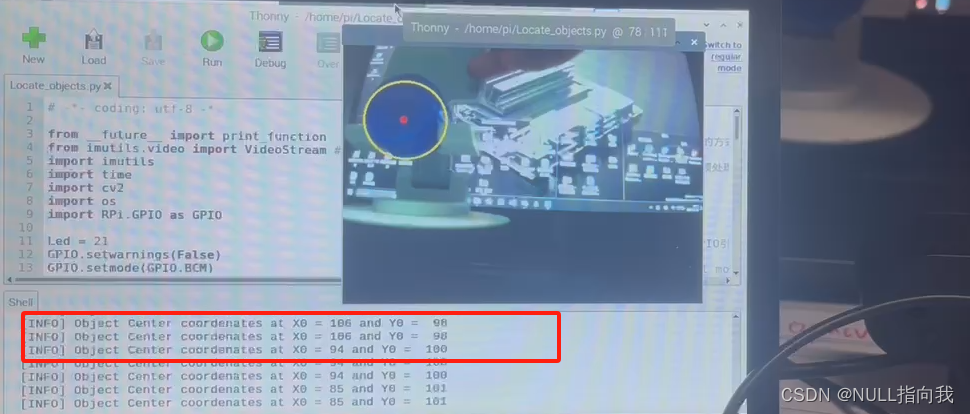
树莓派4B_OpenCv学习笔记15:OpenCv定位物体实时坐标
今日继续学习树莓派4B 4G:(Raspberry Pi,简称RPi或RasPi) 本人所用树莓派4B 装载的系统与版本如下: 版本可用命令 (lsb_release -a) 查询: Opencv 版本是4.5.1: 今日学习 OpenCv定位物体实时位置,代码来源是…...

MySQL之如何定位慢查询
1、如何定位慢查询 1.1、使用开源工具 调试工具:Arthas 运维工具:Promethuss、Skywalking 1.2、MySQL自带慢日志 慢查询日志记录了所有执行时间超过指定参数(long_query_time,单位:秒,默认10秒&#x…...

Open3D 删除点云中重复的点
目录 一、算法原理1、重叠点2、主要函数二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法原理 1、重叠点 原始点云克隆一份 构造重叠区域 合并点云获得重叠点 2、主要…...

填报志愿选专业是兴趣重要还是前景重要?
进行专业评估,找到一个适合自己的专业是一件非常困难的事情。在进行专业选择时,身上理想化色彩非常严重的人,会全然不顾及他人的劝阻,义无反顾的以兴趣为主,选择自己热爱的专业。一些较多考虑他人建议,能听…...

python开发基础——day9 函数基础与函数参数
一、初识函数(function) 编程函数!数学函数,里面的是逻辑,功能,而不是套公式 编程函数的作用实现特定操作的一段代码 你现在请客,每个人都点同样的一份吃的,请100个人 1.薯条 2.上校鸡块 3.可乐 那…...
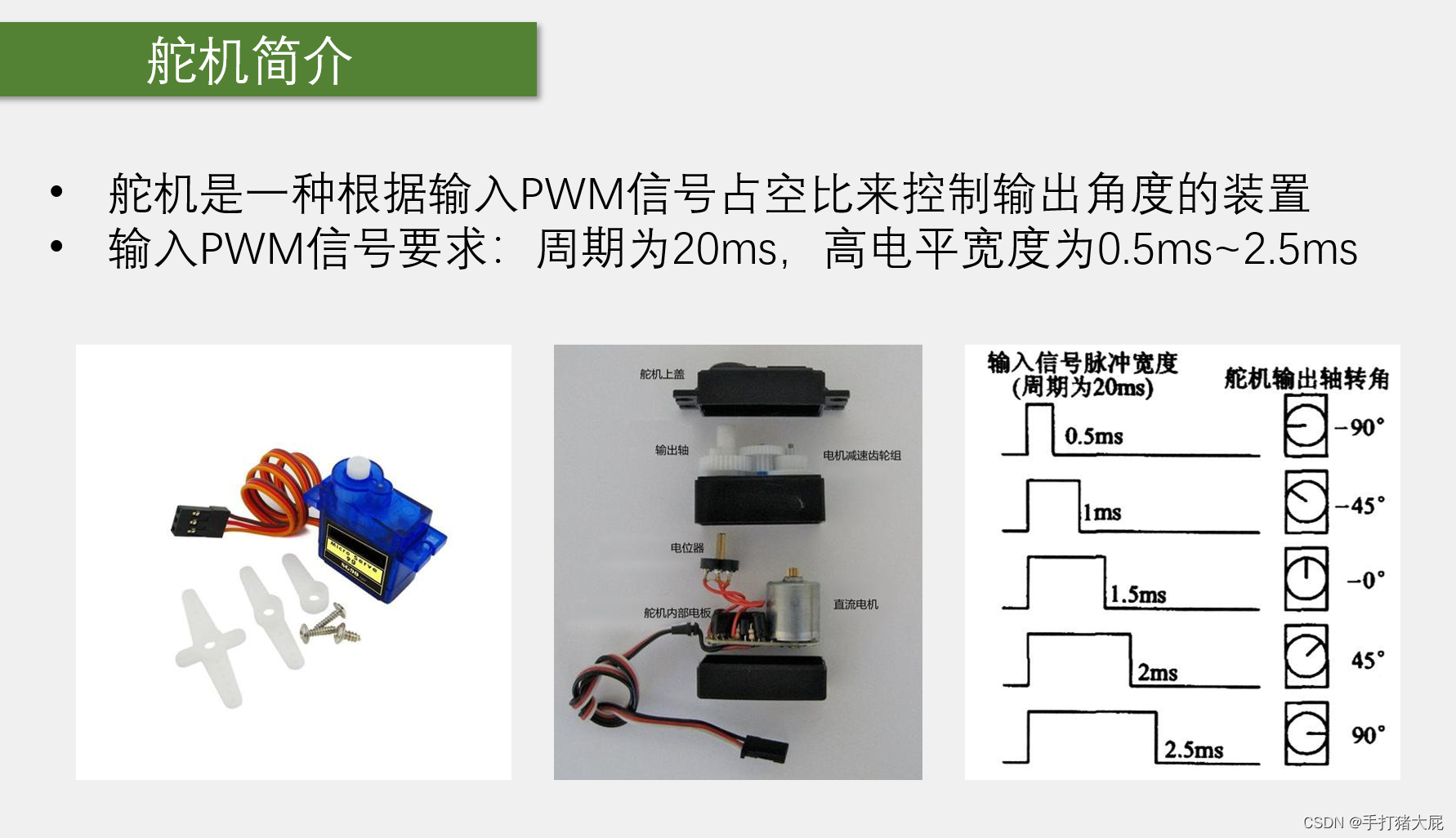
STM32——使用TIM输出比较产生PWM波形控制舵机转角
一、输出比较简介: 只有高级定时器和通用寄存器才有输入捕获/输出比较电路,他们有四个CCR(捕获/比较寄存器),共用一个CNT(计数器),而输出比较功能是用来输出PWM波形的。 红圈部分…...
(Python))
第十五章 集合(set)(Python)
文章目录 前言一、集合 前言 集合(set)是一个无序的不重复元素序列。 一、集合 set {1, 2, 3, 4}...

面试-javaIO机制
1.BIO BIO:是传统的javaIO以及部分java.net下部分接口和类。例如,socket,http等,因为网络通信同样是IO行为。传统IO基于字节流和字符流进行操作。提供了我们最熟悉的IO功能,譬如基于字节流的InputStream 和OutputStream.基于字符流…...

在.NET Core中,config和ConfigureServices的区别和作用
在.NET Core中,config和ConfigureServices是两个不同的概念,它们在应用程序的启动和配置过程中扮演着不同的角色。 ConfigureServices:这是ASP.NET Core应用程序中的一个方法,位于Startup类的内部。它的作用是配置依赖注入(DI)容器…...

App Inventor 2 如何实现多个定时功能?
1、可以使用多个“计时器”组件。 2、也可以用一个计时器,定时一分钟。也就是一分钟就会触发一次事件执行,定义一个全局数字变量,在事件中递增,用逻辑判断这个变量的值即可完成多个想要定时的任务(о∀о) 代码块请参考…...

技术驱动的音乐变革:AI带来的产业重塑
📑引言 近一个月来,随着几款音乐大模型的轮番上线,AI在音乐产业的角色迅速扩大。这些模型不仅将音乐创作的门槛降至前所未有的低点,还引发了一场关于AI是否会彻底颠覆音乐行业的激烈讨论。从初期的兴奋到现在的理性审视࿰…...
重生之我要学后端0--HTTP协议和RESTful APIs
http和RESTful APIs HTTP协议RESTful APIs设计RESTful API设计实例 HTTP协议 HTTP(超文本传输协议)是用于分布式、协作式和超媒体信息系统的应用层协议。它是网页数据通讯的基础。工作原理简述如下: 客户端请求(Request…...
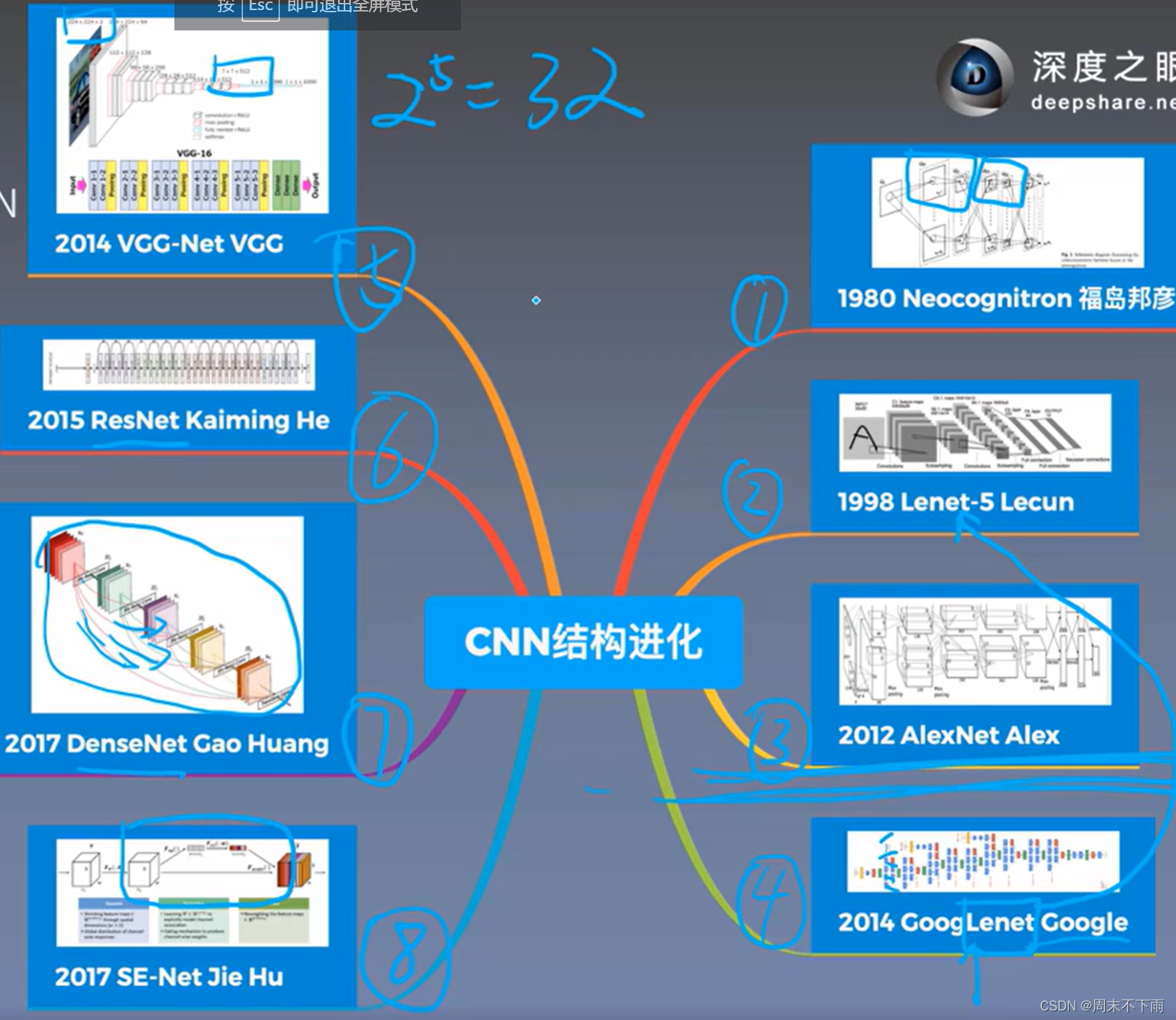
深度之眼(二十八)——神经网络基础知识(三)-卷积神经网络
文章目录 一、前言二、卷积操作2.1 填充(padding)2.2 步长2.3 输出特征图尺寸计算2.4 多通道卷积 三、池化操作四、Lenet-5及CNN结构进化史4.1 Lenet-5 一、前言 卷积神经网络–AlexNet(最牛)-2012 Lenet-5-大规模商用(1989) 二、…...

AI Infra简单记录
向量数据库的作用 1. 在AI大模型训练过程中,向量数据库可以有效提升数据检索、特征提取等任务的效率。 2、在AI大模型推理过程中,向量数据库为大模型提供外挂知识库,提升模型时效性与准确性,提供缓存能力,减少调用开…...

三英战吕布 | 第5集 | 温酒斩华雄 | 竖子不足与谋 | 三国演义 | 逐鹿群雄
🙋大家好!我是毛毛张! 🌈个人首页: 神马都会亿点点的毛毛张 📌这篇博客分享的是《三国演义》文学剧本第Ⅰ部分《群雄逐鹿》的第5️⃣集《三英战吕布》的经典语句和文学剧本全集台词 文章目录 1.经典语句2.文学剧本台…...

【C语言】自定义类型:结构体
目录 1. 结构体类型的声明 1.1. 结构的一般声明 1.2. 结构的特殊声明 2. 结构体变量的创建和初始化 3. 结构体的自引用 4. 结构体内存对齐 4.1. 对其规则(面试考点) 4.2. 为什么存在内存对齐? 4.2.1. 平台原因(移植…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
