【多维动态规划】Leetcode 97. 交错字符串【中等】
交错字符串
给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空
子字符串
子字符串 是字符串中连续的 非空 字符序列。
- s = s1 + s2 + … + sn
- t = t1 + t2 + … + tm
- |n - m| <= 1
- 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + … 或者 t1 + s1 + t2 + s2 + t3 + s3 + …
注意:a + b 意味着字符串 a 和 b 连接。
示例 1:
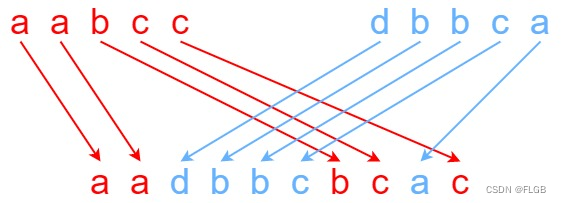
输入:s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出:true
解题思路
定义一个二维布尔数组 dp,其中 dp[i][j] 表示 s3 的前 i + j 个字符是否可以由s1 的前 i 个字符和 s2 的前 j 个字符交错组成。具体的递推关系如下:
初始条件:
- dp[0][0] = true,表示两个空字符串可以组成空字符串。
递推关系:
-
如果 dp[i-1][j] 为真且 s1[i-1] == s3[i + j - 1],则 dp[i][j] = true。
dp[i-1][j] 表示 s3 的前 i + j - 1 个字符可以通过 s1 的前 i-1 个字符和 s2 的前 j 个字符交错组成。
如果 s1 的第 i 个字符 s1[i-1] 等于 s3 的第 i + j 个字符 s3[i + j - 1],
则可以在 s3 的前 i + j - 1 个字符的基础上加上 s1 的第 i 个字符组成 s3 的前 i + j 个字符。
因此,dp[i][j] = true。 -
同理,如果 dp[i][j-1] 为真且 s2[j-1] == s3[i + j - 1],则 dp[i][j] = true。
最终结果:
- dp[s1.length()][s2.length()] 表示 s3 是否可以由 s1 和 s2 交错组成。
Java实现
public class InterleavingString {public boolean isInterleave(String s1, String s2, String s3) {int m = s1.length();int n = s2.length();if (m + n != s3.length()) {return false;}boolean[][] dp = new boolean[m + 1][n + 1];dp[0][0] = true;// 初始化第一列for (int i = 1; i <= m; i++) {dp[i][0] = dp[i-1][0] && s1.charAt(i-1) == s3.charAt(i-1);}// 初始化第一行for (int j = 1; j <= n; j++) {dp[0][j] = dp[0][j-1] && s2.charAt(j-1) == s3.charAt(j-1);}// 填充 dp 表for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = (dp[i-1][j] && s1.charAt(i-1) == s3.charAt(i + j - 1)) || (dp[i][j-1] && s2.charAt(j-1) == s3.charAt(i + j - 1));}}return dp[m][n];}// 测试用例public static void main(String[] args) {InterleavingString solution = new InterleavingString();System.out.println(solution.isInterleave("aabcc", "dbbca", "aadbbcbcac")); // 期望输出: trueSystem.out.println(solution.isInterleave("aabcc", "dbbca", "aadbbbaccc")); // 期望输出: false}
}时间空间复杂度
- 时间复杂度:O(m * n),其中 m 是 s1 的长度,n 是 s2 的长度,需要遍历整个 dp 数组。
- 空间复杂度:O(m * n),需要一个二维数组 dp 存储中间结果。
相关文章:

【多维动态规划】Leetcode 97. 交错字符串【中等】
交错字符串 给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。 两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串 子字符串 是字符串中连续的 非空 字符序列。 s s1 s2 … snt…...

【JavaScript脚本宇宙】精通前端开发:六大热门CSS框架详解
前端开发的利器:深入了解六大CSS框架 前言 在现代Web开发中,选择适合的前端框架和工具包是构建高效、响应式和美观的网站或应用程序的关键。本文将详细介绍六个广受欢迎的CSS框架:Bootstrap、Bulma、Tailwind CSS、Foundation、Materialize…...

开发技术-Java集合(List)删除元素的几种方式
文章目录 1. 错误的删除2. 正确的方法2.1 倒叙删除2.2 迭代器删除2.3 removeAll() 删除2.4 removeIf() 最简单的删除 3. 总结 1. 错误的删除 在写代码时,想将其中的一个元素删除,就遍历了 list ,使用了 remove(),发现效果并不是想…...

c++ 递归
递归函数是指在函数定义中调用自身的函数。C语言也支持递归函数。 下面是一个使用递归函数计算阶乘的例子: #include <iostream> using namespace std;int factorial(int n) {// 基本情况,当 n 等于 0 或 1 时,阶乘为 1if (n 0 || n…...
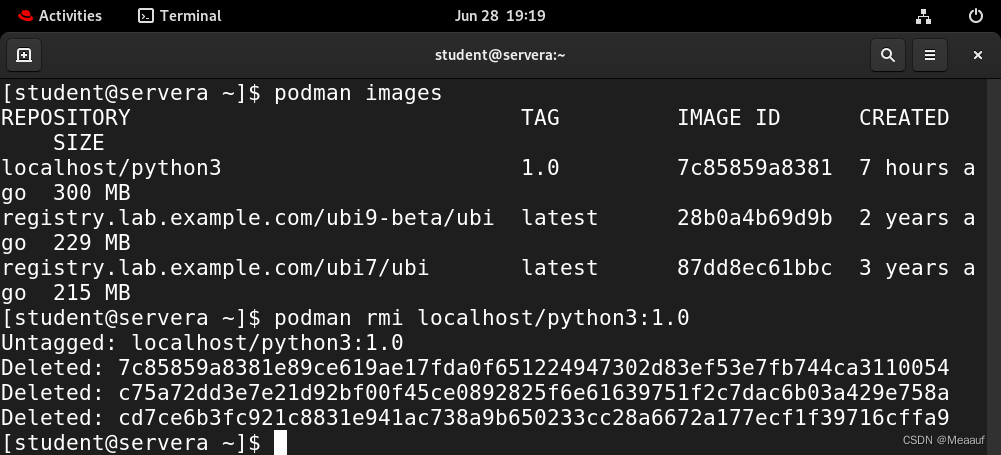
RedHat9 | podman容器
1、容器技术介绍 传统问题 应用程序和依赖需要一起安装在物理主机或虚拟机上的操作系统应用程序版本比当前操作系统安装的版本更低或更新两个应用程序可能需要某一软件的不同版本,彼此版本之间不兼容 解决方式 将应用程序打包并部署为容器容器是与系统的其他部分…...

边缘计算项目有哪些
边缘计算项目在多个领域得到了广泛的应用,以下是一些典型的边缘计算项目案例: 1. **智能交通系统**:通过在交通信号灯、监控摄像头等设备上部署边缘计算,可以实时分析交通流量,优化交通信号控制,减少拥堵&…...

计算fibonacci数列每一项时所需的递归调用次数
斐波那契数列是一个经典的数列,其中每一项是前两项的和,定义为: [ F(n) F(n-1) F(n-2) ] 其中,( F(0) 0 ) 和 ( F(1) 1 )。 对于计算斐波那契数列的第 ( n ) 项,如果使用简单的递归方法,其时间复杂度是…...

【教学类65-05】20240627秘密花园涂色书(中四班练习)
【教学类65-03】20240622秘密花园涂色书03(通义万相)(A4横版1张,一大 68张纸136份)-CSDN博客 背景需求: 打印以下几款秘密花园样式(每款10份)给中四班孩子玩一下,看看效果 【教学类…...
)
Python 学习之基础语法(一)
Python的语法基础主要包括以下几个方面,下面将逐一进行分点表示和归纳: 一、基本语法 1. 注释 a. 单行注释:使用#开头,例如# 这是一个单行注释。 b. 多行注释:使用三引号(可以是三个单引号或三个双引号&…...
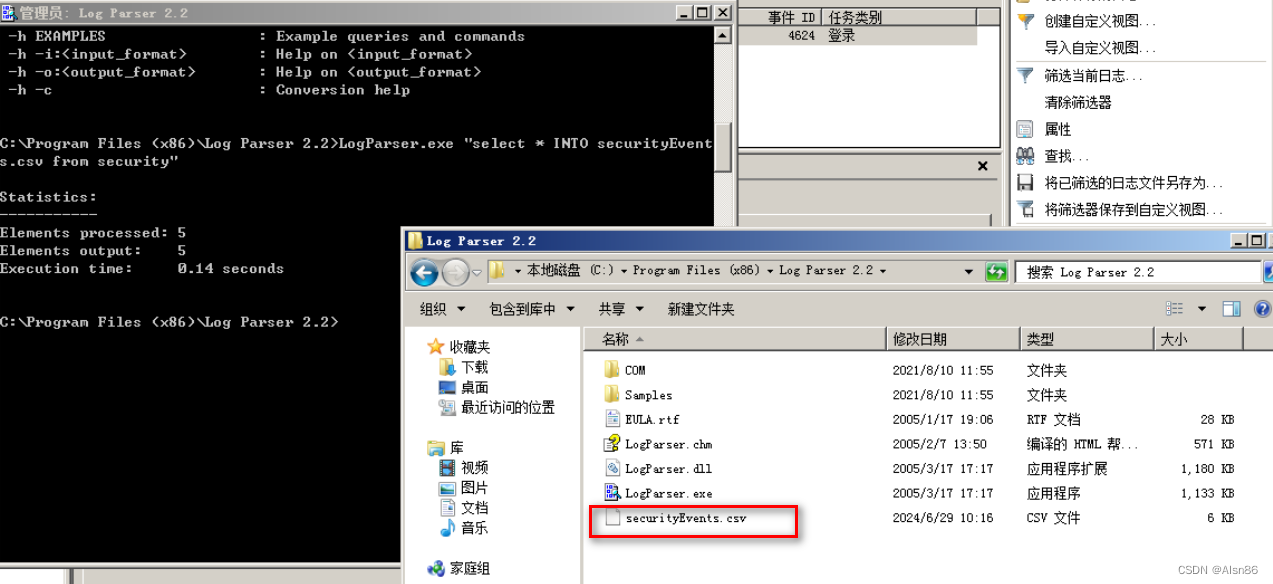
日志分析-windows系统日志分析
日志分析-windows系统日志分析 使用事件查看器分析Windows系统日志 cmd命令 eventvwr 筛选 清除日志、注销并重新登陆,查看日志情况 Windows7和Windowserver2008R2的主机日志保存在C:\Windows\System32\winevt\Logs文件夹下,Security.evtx即为W…...

【ARM】MDK工程切换高版本的编译器后出现error A1137E报错
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 解决工程从Compiler 5切换到Compiler 6进行编译时出现一些非语法问题上的报错。 2、 问题场景 对于一些使用Compiler 5进行编译的工程,要切换到Compiler 6进行编译的时候,原本无任何报错警告…...

深入 SSH:解锁本地转发、远程转发和动态转发的潜力
文章目录 前言一、解锁内部服务:SSH 本地转发1.1 什么是 SSH 本地转发1.2 本地转发应用场景 二、打开外部访问大门:SSH 远程转发2.1 什么是 SSH 远程转发2.2 远程转发应用场景 三、动态转发:SSH 让你拥有自己的 VPN3.1 什么是 SSH 动态转发3.…...

python如何把一个函数的返回值,当成这个函数的参数值
python如何把一个函数的返回值,当成这个函数的参数值 1. 递归调用 递归是一种函数自己调用自己的方法。在递归调用中,你可以将前一次调用的返回值作为下一次调用的参数。 def recursive_function(x):# 函数逻辑if 条件满足:return 结果else:return rec…...

【融合ChatGPT等AI模型】Python-GEE遥感云大数据分析、管理与可视化及多领域案例应用
随着航空、航天、近地空间遥感平台的持续发展,遥感技术近年来取得显著进步。遥感数据的空间、时间、光谱分辨率及数据量均大幅提升,呈现出大数据特征。这为相关研究带来了新机遇,但同时也带来巨大挑战。传统的工作站和服务器已无法满足大区域…...
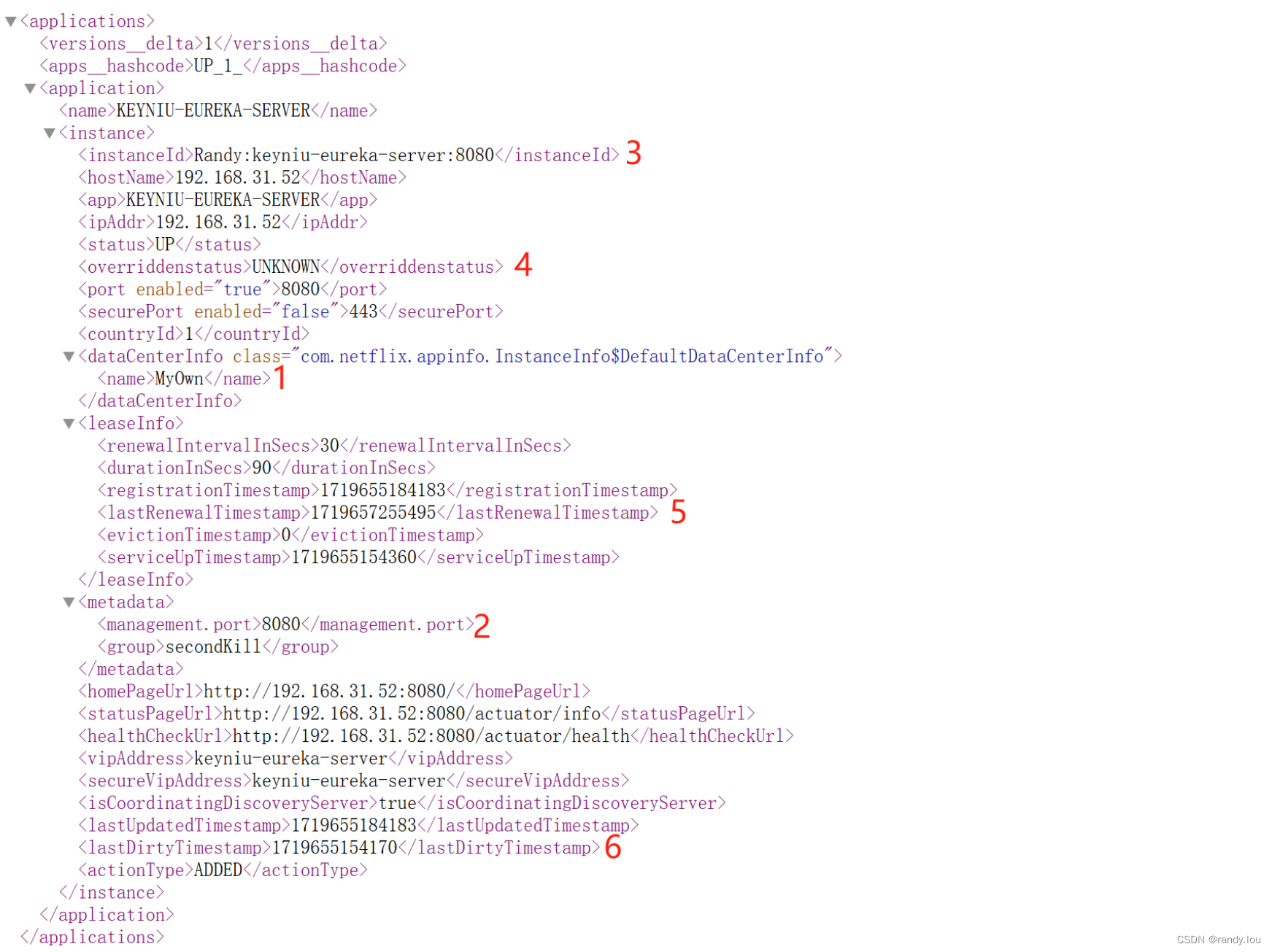
SpringBoot: Eureka入门
1. IP列表 公司发展到一定的规模之后,应用拆分是无可避免的。假设我们有2个服务(服务A、服务B),如果服务A要调用服务B,我们能怎么做呢?最简单的方法是让服务A配置服务B的所有节点的IP,在服务A内部做负载均衡调用服务B…...

Typescript 【实用教程】(2024最新版)含类型声明,类型断言,函数,接口,泛型等
简介 TypeScript 是 JavaScript 的超集,是 JavaScript(弱类型语言) 的强类型版本。 拥有类型机制文件后缀 .tsTypescript type ES6TypeScript 和 JavaScript 的关系类似 less 和 css 的关系TypeScript对 JavaScript 添加了一些扩展&#x…...
智慧校园-实训管理系统总体概述
智慧校园实训管理系统,专为满足高等教育与职业教育的特定需求而设计,它代表了实训课程管理领域的一次数字化飞跃。此系统旨在通过革新实训的组织结构、执行流程及评估标准,来增强学生的实践操作技能和教师的授课效率,为社会输送具…...

如何用GPT开发一个基于 GPT 的应用?
原文发自博客:GPT应用开发小记 如何开发一个基于 GPT 的应用?答案就在问题里,那就是用 GPT 来开发基于 GPT 的应用。本文以笔者的一个开源项目 myGPTReader 为例,分享我是如何基于 GPT 去开发这个系统的,这个系统的功能…...
)
大数据生态体系中各组件的区别面试题(更新)
一、MapReduce与Spark有什么区别? 1、处理方式: MapReduce基于磁盘处理数据,将中间结果保存到磁盘中,减少了内存占用,计算速度慢。 基于内存处理数据,将计算的中间结果保存到内存中,计算速度快。2、资源申请方式&…...

数字信号处理实验一(离散信号及离散系统的MATLAB编程实现)
实验要求: 离散信号及离散系统的MATLAB编程实现(2学时) 要求: 编写一程序,输出一定长度(点数),具有一定幅度、(角)频率和初始相位的实(或复&…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
