代码随想录-Day43
52. 携带研究材料(第七期模拟笔试)
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等,它们各自占据不同的重量,并且具有不同的价值。
小明的行李箱所能承担的总重量为 N,问小明应该如何抉择,才能携带最大价值的研究材料,每种研究材料可以选择无数次,并且可以重复选择。
输入描述
第一行包含两个整数,N,V,分别表示研究材料的种类和行李空间
接下来包含 N 行,每行两个整数 wi 和 vi,代表第 i 种研究材料的重量和价值
输出描述
输出一个整数,表示最大价值。
输入示例
4 5
1 2
2 4
3 4
4 5
输出示例
10

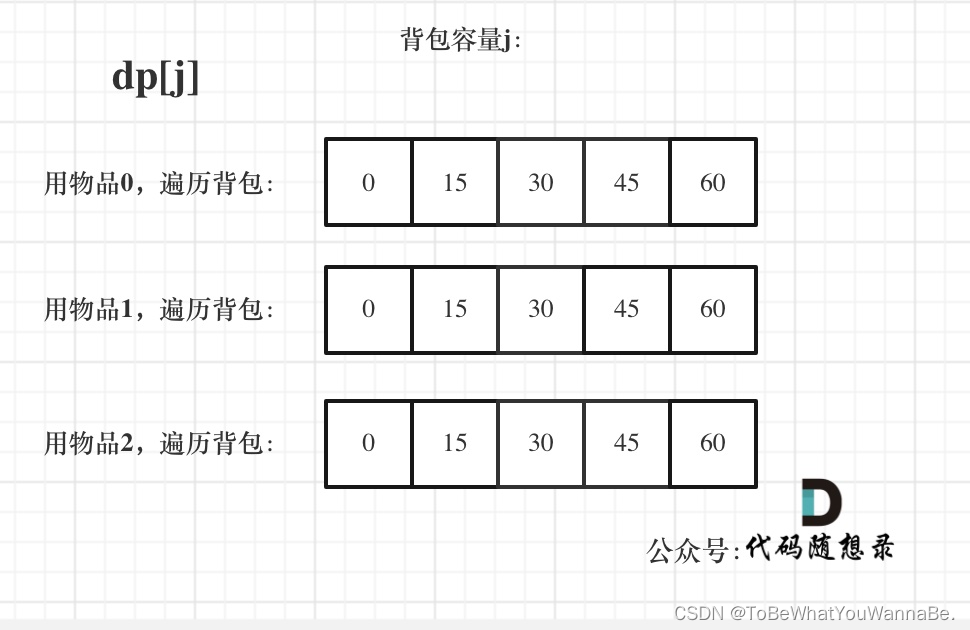
方法一:
//先遍历物品,再遍历背包
private static void testCompletePack(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 0; i < weight.length; i++){ // 遍历物品for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}
这段代码是一个使用动态规划解决0-1背包问题的Java示例。0-1背包问题是指有N件物品和一个容量为W的背包,每种物品都有自己的重量和价值,在不超过背包所能装载的总重量的前提下,如何选择装入背包的物品,使得背包中物品的总价值最大。
代码解释如下:
- 定义了物品的重量数组
weight和价值数组value,以及背包的最大容量bagWeight。 - 创建一个数组
dp,长度为bagWeight + 1,用于存储每个背包容量下的最大价值。初始化时,默认值都为0,表示背包为空时的价值为0。 - 外层循环(
for (int i = 0; i < weight.length; i++))遍历每一件物品。 - 内层循环(
for (int j = weight[i]; j <= bagWeight; j++))遍历从当前物品的重量开始到背包最大容量的所有可能的背包容量。这样设置是因为如果背包容量小于当前物品的重量,这件物品不可能被放入背包中,所以不必考虑。 - 在内层循环中,使用
Math.max()函数比较两种情况:一是不把当前物品放入背包中时的最大价值dp[j],二是把当前物品放入背包后剩余空间的最大价值dp[j - weight[i]] + value[i],取两者的较大值作为新的dp[j],即更新这个背包容量下的最大价值。 - 最后,通过遍历并打印数组
dp,可以得到不同背包容量下能够达到的最大价值。
这段代码执行后,会输出一个序列,表示从容量为0到容量为bagWeight的背包能够装入物品的最大价值。最后一项即为给定背包容量下的最大价值。
方法二:
//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量for (int j = 0; j < weight.length; j++){ // 遍历物品if (i - weight[j] >= 0){dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);}}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}
这段代码同样是解决0-1背包问题的Java实现,但它的遍历顺序与上一个示例相反:首先遍历背包的容量,然后遍历物品。下面是这段代码的解释:
-
定义变量:与前一个示例相同,定义了物品的重量数组
weight、价值数组value以及背包的最大容量bagWeight。同时初始化了一个dp数组来记录不同背包容量下的最大价值。 -
外层循环 (
for (int i = 1; i <= bagWeight; i++)):这次是先从背包容量为1开始,直到遍历到最大背包容量bagWeight。这里从1开始是因为容量为0的情况在初始化时已经设定为0,无需处理。 -
内层循环 (
for (int j = 0; j < weight.length; j++)):遍历每一个物品。与前一个示例的遍历顺序相反。 -
条件判断 (
if (i - weight[j] >= 0)):在尝试将当前物品放入背包之前,先检查当前背包的容量i是否至少能放下物品j。这是必要的,因为如果背包容量不足以容纳当前物品,就无需继续计算加入该物品后的价值,直接跳过。 -
价值更新:如果背包容量足够,使用
Math.max()函数比较当前背包容量下的最大价值dp[i]和将当前物品放入背包后剩余空间的最大价值加上当前物品的价值dp[i - weight[j]] + value[j],取较大者作为新的dp[i]。这一步确保了在考虑添加新物品时,背包的价值总是尽可能大。 -
输出结果:最后,遍历并打印数组
dp,展示不同背包容量下可达到的最大价值。最后一项依然是整个问题的解,即背包最大容量为bagWeight时能够装入物品的最大总价值。
这种遍历顺序(先背包容量,后物品)也是解决0-1背包问题的有效方法,它在逻辑上直观地体现了“逐渐增加背包容量并尝试放入所有物品以最大化价值”的过程。
518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入:amount = 3, coins = [2]
输出:0
解释:只用面额 2 的硬币不能凑成总金额 3 。
示例 3:
输入:amount = 10, coins = [10]
输出:1
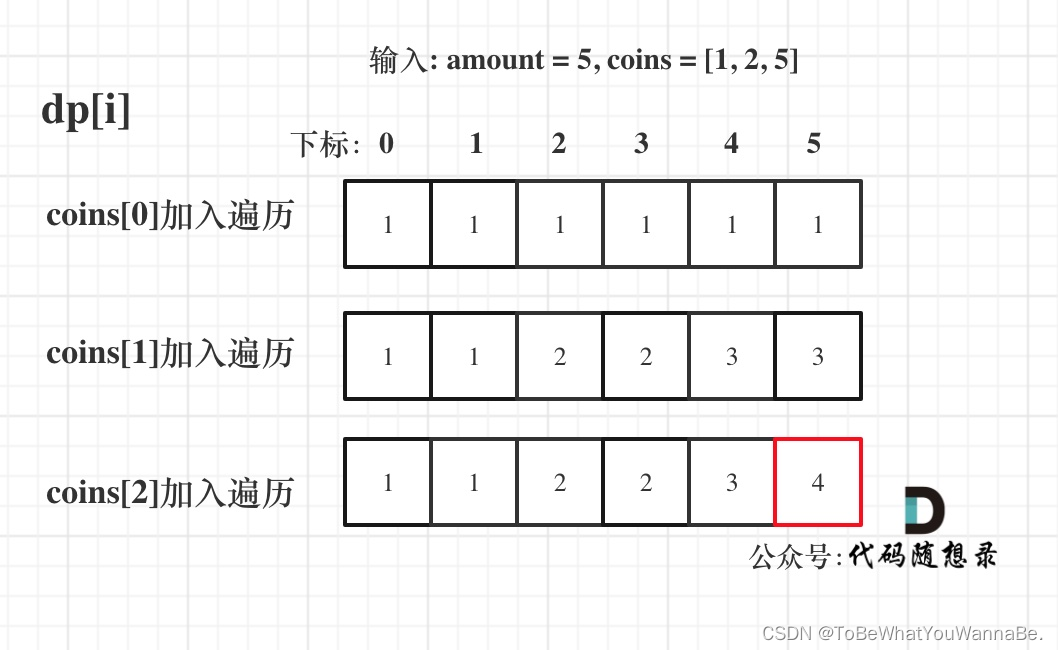
方法一:
class Solution {public int change(int amount, int[] coins) {//递推表达式int[] dp = new int[amount + 1];//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装dp[0] = 1;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {dp[j] += dp[j - coins[i]];}}return dp[amount];}
}
这段代码是Java语言实现的一个解决方案,解决的是找零问题(Coin Change Problem)。给定一定数量的硬币(每种硬币的数量不限)和一个总金额,求出有多少种不同的组合方式可以凑成总金额。这是一个经典的动态规划问题。
具体分析如下:
-
定义状态:
dp[j]表示总额为j时的找零方案数。这是我们要填充的动态规划数组。 -
初始化:
dp[0] = 1,表示当金额为0时,有一种组合方式(即不选任何硬币)。 -
双层循环:
- 外层循环
for (int i = 0; i < coins.length; i++)遍历每一种硬币。 - 内层循环
for (int j = coins[i]; j <= amount; j++)从当前硬币的面值开始,遍历到总金额。这是因为如果当前金额小于硬币的面值,不可能再用这个硬币去凑更小的金额,所以从硬币面值开始是有意义的起始点。
- 外层循环
-
状态转移方程:
dp[j] += dp[j - coins[i]]。对于每一个j,都有两种情况:要么使用当前硬币coins[i],那么剩余的金额就是j - coins[i],方案数就是dp[j - coins[i]];要么不使用当前硬币,直接继承之前的方案数dp[j]。但因为我们要累加所有可能的组合,所以是累加而不是直接赋值。 -
返回结果:最后返回
dp[amount],即为目标总金额的找零方案数。
综上所述,这段代码通过动态规划的方法,高效地计算出了给定硬币种类和总金额下的找零组合数。
方法二:
// 二维dp数组版本,方便理解
class Solution {public int change(int amount, int[] coins) {int[][] dp = new int[coins.length][amount+1];// 初始化边界值for(int i = 0; i < coins.length; i++){// 第一列的初始值为1dp[i][0] = 1;}for(int j = coins[0]; j <= amount; j++){// 初始化第一行dp[0][j] += dp[0][j-coins[0]];}for(int i = 1; i < coins.length; i++){for(int j = 1; j <= amount; j++){if(j < coins[i]) dp[i][j] = dp[i-1][j];else dp[i][j] = dp[i][j-coins[i]] + dp[i-1][j];}}return dp[coins.length-1][amount];}
}
这段代码是另一个版本的解决方案,同样用来解决找零问题(Coin Change Problem),但是使用了二维动态规划数组来实现,这有助于更直观地理解动态规划的状态转移过程。下面是对代码的详细解析:
-
初始化二维dp数组:
int[][] dp = new int[coins.length][amount+1];,其中dp[i][j]表示在前i+1种硬币中选取,凑成总额为j的组合数。 -
初始化边界值:
- 对于每一行(每种硬币)的首列(总额为0的情况),都只有1种方法,即不选择任何硬币,因此
dp[i][0] = 1;。 - 初始化第一行时,需要根据第一种硬币的不同面额来填充。对于每一列
j(从硬币面值开始到总金额),如果可以由若干个第一种硬币组成,即j >= coins[0],则dp[0][j] += dp[0][j-coins[0]],意味着可以通过在已有的组合基础上再添加一个硬币来得到这个总额。
- 对于每一行(每种硬币)的首列(总额为0的情况),都只有1种方法,即不选择任何硬币,因此
-
状态转移:核心的双层循环遍历每一种硬币和每一个可能的总金额。
- 对于
i > 0(即除了第一种硬币之外的其他硬币)和j > 0(即除了总额为0之外的情况),有两种选择:- 不使用第
i种硬币,这时的组合数与前i-1种硬币凑成总额j的组合数相同,即dp[i][j] = dp[i-1][j]。 - 使用至少一个第
i种硬币,剩余的金额为j - coins[i],这时的组合数是在总额减去当前硬币面值后,使用全部i种硬币的组合数,即dp[i][j-coins[i]]。因此,这两种情况的组合数相加即为最终的dp[i][j]。 - 注意,当
j < coins[i],即当前总额无法再使用第i种硬币时,不应考虑使用该硬币的情况,直接继承前i-1种硬币的结果。
- 不使用第
- 对于
-
返回结果:最终答案为
dp[coins.length-1][amount],即在所有硬币中选择,凑成总金额为amount的所有可能组合数。
这个版本虽然占用更多的空间,但它清晰地展现了每一步决策的过程,便于理解和分析动态规划的状态转移逻辑。
377. 组合总和 Ⅳ
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4
输出:7
解释:
所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意,顺序不同的序列被视作不同的组合。
示例 2:
输入:nums = [9], target = 3
输出:0

class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.length; j++) {if (i >= nums[j]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
}
这段代码是用来解决完全背包问题(Unbounded Knapsack Problem)的一个变种——求解组合总和IV的问题。给定一个由正整数组成的数组 nums 和一个目标整数 target,找出并返回可以由 nums 中的数字组成的、和为目标整数 target 的不同非空组合的数量。每个数组中的数字可以无限制次数地重复被选取。
这里是使用一维动态规划的解决方案,具体解析如下:
-
初始化dp数组:
int[] dp = new int[target + 1];,其中dp[i]表示总和为i的组合数。初始化dp[0] = 1,表示总和为0的情况只有一个组合(即不选任何数)。 -
双层循环:
- 外层循环
for (int i = 0; i <= target; i++)遍历从0到目标值target的每一个可能的总和。 - 内层循环
for (int j = 0; j < nums.length; j++)遍历数组nums中的所有数字。
- 外层循环
-
状态转移:对于每个总和
i,考虑数组中的每个数nums[j],如果当前总和i大于等于这个数(i >= nums[j]),说明可以使用nums[j]来构成总和i的一部分,那么dp[i]应该加上总和为i - nums[j]时的组合数,即dp[i] += dp[i - nums[j]]。这样就实现了从已知的较小问题的解来构建更大问题解的过程。 -
返回结果:最终答案是
dp[target],即所有元素和为目标值target的组合总数。
这个解法有效地利用了动态规划避免了重复计算,降低了时间复杂度。其时间复杂度大致为O(n * target),其中n为数组 nums 的长度,target为所求的目标和。
57. 爬楼梯(第八期模拟笔试)
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
输入描述
输入共一行,包含两个正整数,分别表示n, m
输出描述
输出一个整数,表示爬到楼顶的方法数。
输入示例
3 2
输出示例
3
import java.util.Scanner;
class climbStairs{public static void main(String [] args){Scanner sc = new Scanner(System.in);int m, n;while (sc.hasNextInt()) {// 从键盘输入参数,中间用空格隔开n = sc.nextInt();m = sc.nextInt();// 求排列问题,先遍历背包再遍历物品int[] dp = new int[n + 1];dp[0] = 1;for (int j = 1; j <= n; j++) {for (int i = 1; i <= m; i++) {if (j - i >= 0) dp[j] += dp[j - i];}}System.out.println(dp[n]);}}
}
这段Java代码实现了一个爬楼梯问题的解法,不过这里的描述有误,实际上解决的是完全背包问题的一个变形,而非直接的爬楼梯问题。但我们可以按照代码逻辑来理解它所解决的问题:给定一个人可以一次跳跃1到m个台阶,问他有多少种不同的方式跳上n阶楼梯。
解析如下:
- 导入Scanner类:用于从控制台读取用户输入的数据。
- 定义主函数:在主函数中,程序通过
Scanner对象sc读取两个整数,分别代表楼梯阶数n和每次跳跃的最大阶数m。 - 初始化动态规划数组:创建一个大小为
n+1的数组dp,其中dp[j]表示到达第j阶楼梯的不同方法数。初始化dp[0]=1,表示站在起点(0阶)只有1种方法(即不跳)。 - 双层循环:
- 外层循环
for (int j = 1; j <= n; j++)遍历从第1阶到第n阶楼梯。 - 内层循环
for (int i = 1; i <= m; i++)遍历每次跳跃的阶数,从1跳到m。 - 如果当前阶数
j大于或等于跳跃的阶数i,则可以从j-i阶跳到第j阶,因此dp[j]需要累加dp[j-i],即之前阶数到达方式的总数。
- 外层循环
- 输出结果:最后,输出
dp[n],即到达第n阶楼梯的所有不同方法数。
尽管注释提到“求排列问题,先遍历背包再遍历物品”,但实际上这段代码解决的是一个组合问题,更准确地说是完全背包问题的一种特殊情况,用来计算在给定步长限制下到达特定楼层的方案数。
相关文章:

代码随想录-Day43
52. 携带研究材料(第七期模拟笔试) 小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等…...
C++——探索智能指针的设计原理
前言: RAII是资源获得即初始化, 是一种利用对象生命周期来控制程序资源地手段。 智能指针是在对象构造时获取资源, 并且在对象的声明周期内控制资源, 最后在对象析构的时候释放资源。注意, 本篇文章参考——C 智能指针 - 全部用法…...

办公效率新高度:利用办公软件实现文件夹编号批量复制与移动,轻松管理文件
在数字化时代,我们的工作和生活都围绕着海量的数据和文件展开。然而,随着数据量的不断增加,如何高效地管理这些数字资产成为了摆在我们面前的一大难题。今天,我要向您介绍一种革命性的方法——利用办公软件实现文件夹编号批量复制…...
Windows kubectl终端日志聚合(wsl+ubuntu+cmder+kubetail)
Windows kubectl终端日志聚合 一、kubectl终端日志聚合二、windows安装ubuntu子系统1. 启用wsl支持2. 安装所选的 Linux 分发版 三、ubuntu安装kubetail四、配置cmder五、使用 一、kubectl终端日志聚合 k8s在实际部署时,一般都会采用多pod方式,这种情况下…...

【MySQL】数据库——事务
一.事务概念 事务是一种机制、一个操作序列,包含了一组数据库操作命令,并且把所有的命令作为一个整体一起向系统提交或撤销操作请求,即这一组数据库命令要么都执行,要么都不执行事务是一个不可分割的工作逻辑单元,在数…...
)
python代码缩进规范(2空格或4空格)
C、C、Java、C#、Rust、Go、JavaScript 等常见语言都是用"{“和”}"来标记一个块作用域的开始和结束,而Python 程序则是用缩进来表示块作用域的开始和结束: 作用域是编程语言里的一个重要的概念,特别是块作用域,编程语言…...

前后端分离的后台管理系统开发模板(带你从零开发一套自己的若依框架)上
前言: 目前,前后端分离开发已经成为当前web开发的主流。目前最流行的技术选型是前端vue3后端的spring boot3,本次。就基于这两个市面上主流的框架来开发出一套基本的后台管理系统的模板,以便于我们今后的开发。 前端使用vue3ele…...

【C++ | 委托构造函数】委托构造函数 详解 及 例子源码
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

iCloud邮件全攻略:设置与使用终极指南
标题:iCloud邮件全攻略:设置与使用终极指南 摘要 iCloud邮件是Apple提供的一项邮件服务,允许用户在所有Apple设备上访问自己的邮件。本文将详细介绍如何在各种设备和邮件客户端上设置和使用iCloud邮件账户,确保用户能够充分利用…...

【计算机毕业设计】基于微信小程序的电子购物系统的设计与实现【源码+lw+部署文档】
包含论文源码的压缩包较大,请私信或者加我的绿色小软件获取 免责声明:资料部分来源于合法的互联网渠道收集和整理,部分自己学习积累成果,供大家学习参考与交流。收取的费用仅用于收集和整理资料耗费时间的酬劳。 本人尊重原创作者…...

CSS实现动画
CSS实现动画主要有三种方式:transition,transform,和animation1。以下是一些详细的逻辑,实例和注意事项: Transition:transition可以为一个元素在不同状态之间切换的时候定义不同的过渡效果。例如ÿ…...
Python+Pytest+Allure+Yaml+Jenkins+GitLab接口自动化测试框架详解
PythonPytestAllureYaml接口自动化测试框架详解 编撰人:CesareCheung 更新时间:2024.06.20 一、技术栈 PythonPytestAllureYamlJenkinsGitLab 版本要求:Python3.7.0,Pytest7.4.4,Allure2.18.1,PyYaml6.0 二、环境配置 安装python3.7&…...
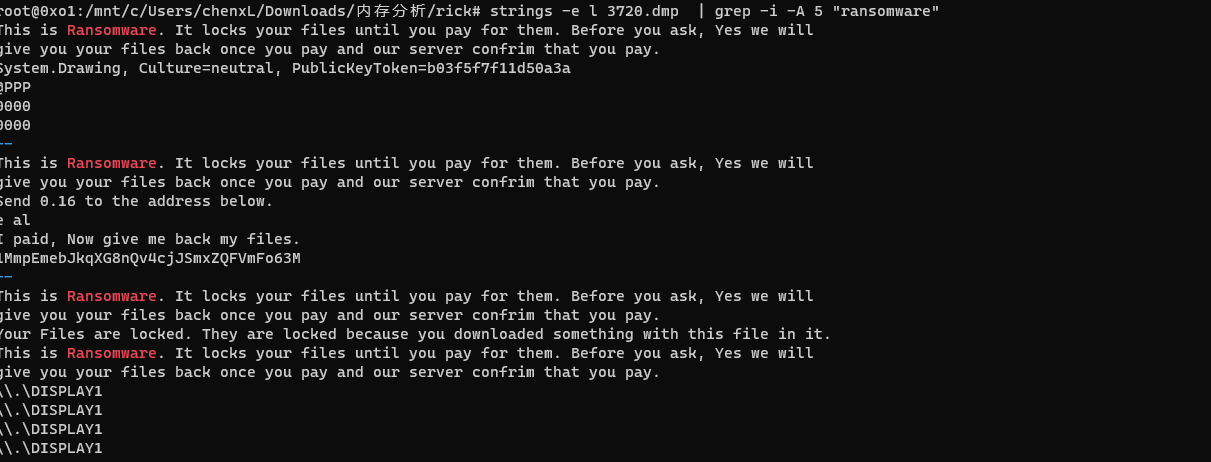
[OtterCTF 2018]Bit 4 Bit
我们已经发现这个恶意软件是一个勒索软件。查找攻击者的比特币地址。** 勒索软件总喜欢把勒索标志丢在显眼的地方,所以搜索桌面的记录 volatility.exe -f .\OtterCTF.vmem --profileWin7SP1x64 filescan | Select-String “Desktop” 0x000000007d660500 2 0 -W-r-…...
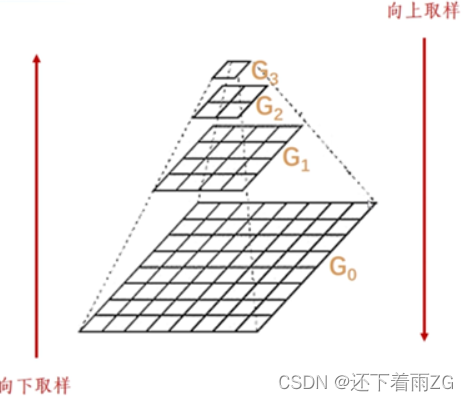
计算机视觉全系列实战教程 (十四):图像金字塔(高斯金字塔、拉普拉斯金字塔)
1.图像金字塔 (1)下采样 从G0 -> G1、G2、G3 step01:对图像Gi进行高斯核卷积操作(高斯滤波)step02:删除所有的偶数行和列 void cv::pyrDown(cv::Mat &imSrc, //输入图像cv::Mat &imDst, //下采样后的输出图像cv::Si…...

正确重写equals和hashcode方法
1. 重写的原因 如有个User对象如下: public class User {private String name;private Integer age; }如果不重写equals方法和hashcode方法,则: public static void main(String[] args) {User user1 new User("userA", 30);Us…...

数据质量管理-时效性管理
前情提要 根据GB/T 36344-2018《信息技术 数据质量评价指标》的标准文档,当前数据质量评价指标框架中包含6评价指标,在实际的数据治理过程中,存在一个关联性指标。7个指标中存在4个定性指标,3个定量指标; 定性指标&am…...

python 实例002 - 数据转换
题目: 有一组用例数据如下: cases [[case_id, case_title, url, data, excepted],[1, 用例1, www.baudi.com, 001, ok],[4, 用例4, www.baudi.com, 002, ok],[2, 用例2, www.baudi.com, 002, ok],[3, 用例3, www.baudi.com, 002, ok],[5, 用例5, www.ba…...

1.k8s:架构,组件,基础概念
目录 一、k8s了解 1.什么是k8s 2.为什么要k8s (1)部署方式演变 (2)k8s作用 (3)Mesos,Swarm,K8S三大平台对比 二、k8s架构、组件 1.k8s架构 2.k8s基础组件 3.k8s附加组件 …...
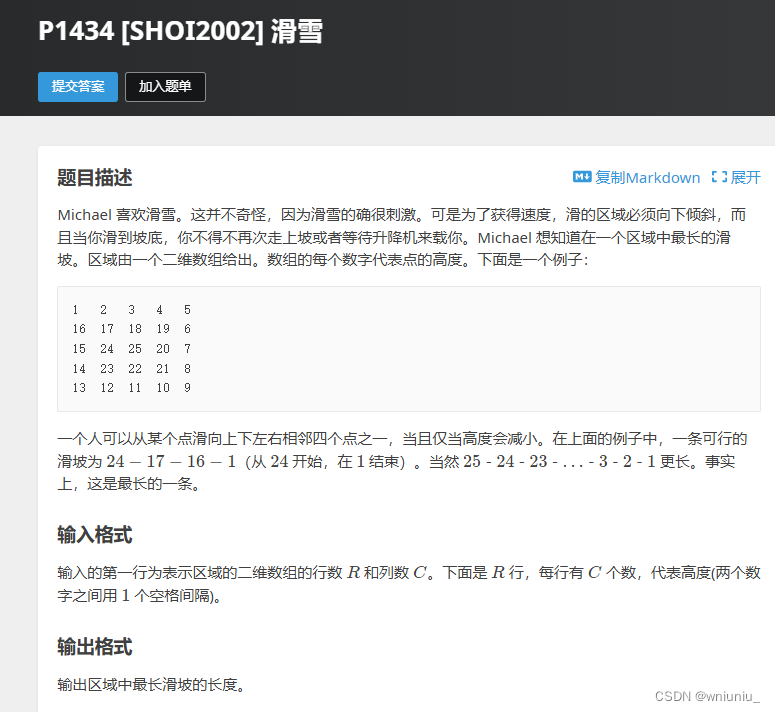
动态规划基础练习
我们需要先从数组较大的开始进行处理,每次考察上下左右的,比较当前存储的最大值和转移来的值,哪一个大一点 #define _CRT_SECURE_NO_WARNINGS #include<bits/stdc.h> using namespace std;int n, m; int a[105][105]; int addx[] { 0,…...

基于Java的地方废物回收机构管理系统
你好呀,我是计算机学姐码农小野!如果有相关需求,可以私信联系我。 开发语言:Java 数据库:MySQL 技术:Java技术,MIS的总体思想,MySQL数据库 工具:Eclipse,…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
