[LeetCode周赛复盘] 第 99 场双周赛20230304
[LeetCode周赛复盘] 第 99 场双周赛20230304
- 一、本周周赛总结
- 二、 [Easy] 2578. 最小和分割
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、[Medium] 2579. 统计染色格子数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、[Medium] 2580. 统计将重叠区间合并成组的方案数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、[Hard] 2581. 统计可能的树根数目
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
- T1 贪心。
- T2 数学/dp。
- T3 线段合并/快速幂取模。
- T4 换根DP。
二、 [Easy] 2578. 最小和分割
链接: 2578. 最小和分割
1. 题目描述
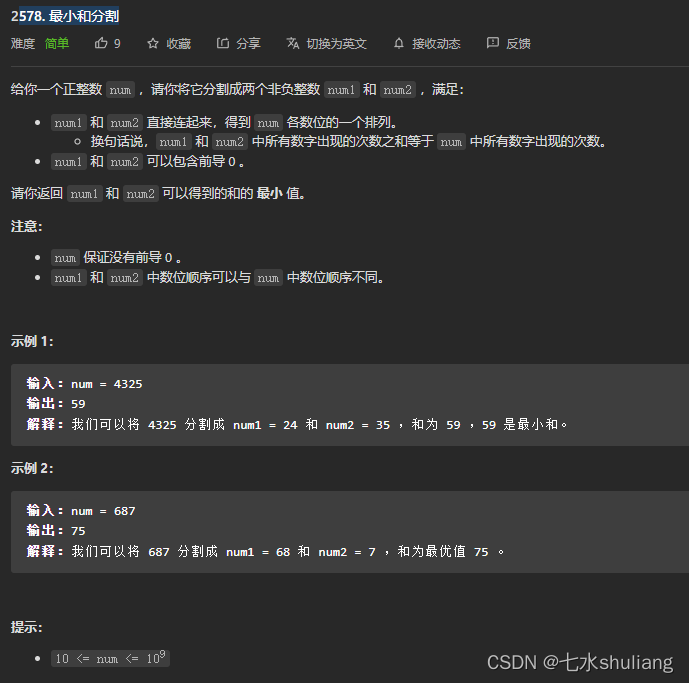
2. 思路分析
- 这题如果不写暴力枚举的话,是个贪心,想了好一会。
- 排序后奇偶交错分配即可。
- 枚举的话,状压枚举可能写的更快一些。
3. 代码实现
class Solution:def splitNum(self, num: int) -> int: s = []for c in str(num):if c != '0':s.append(c)s = sorted(s)n = len(s)h = n // 2a = []b = []for i,c in enumerate(s):if i & 1:b.append(c)else:a.append(c)x = int('0'+''.join(a))y = int('0'+''.join(b))return x + y
三、[Medium] 2579. 统计染色格子数
链接: 2579. 统计染色格子数
1. 题目描述
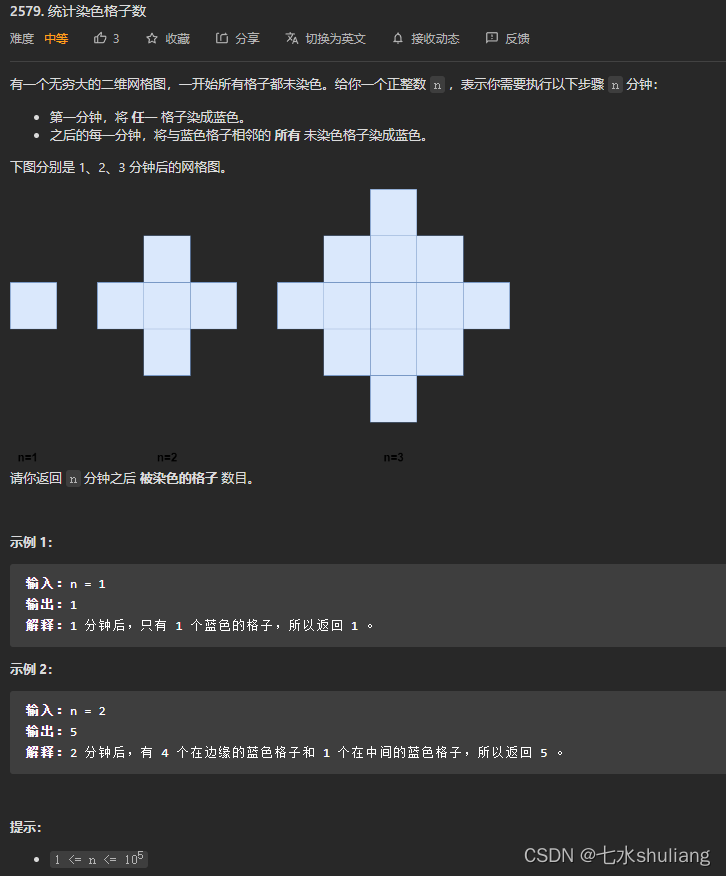
2. 思路分析
数学能力已经退化,比赛时肯定不优先推公式。
- 找规律dp。
- 发现每次增加i*4个。
3. 代码实现
f = [1]*(10**5+1)
x = [1]*(10**5+1)
for i in range(2,10**5+1):x[i] = (i-1)*4f[i] = f[i-1] + x[i]
class Solution:def coloredCells(self, n: int) -> int:return f[n]
四、[Medium] 2580. 统计将重叠区间合并成组的方案数
链接: 2580. 统计将重叠区间合并成组的方案数
1. 题目描述
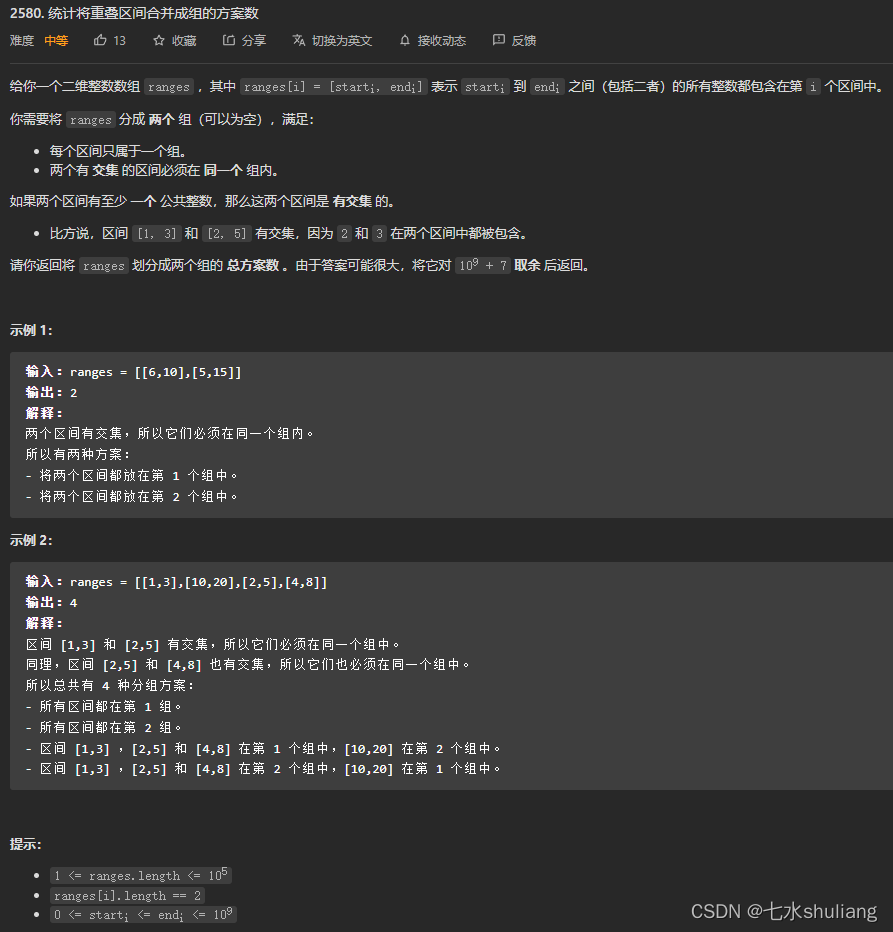
2. 思路分析
- 分析题意发现,有交集的区间一定在一起,那么划分完会变成x个集合,这x个集合分别可以在左边或右边就互不影响了。
- 因此答案就是2**x。
3. 代码实现
MOD = 10 ** 9 + 7
class Solution:def countWays(self, ranges: List[List[int]]) -> int:cnt = 1ranges.sort()print(ranges)p = ranges[0][1]for x,y in ranges:if x <= p:p = max(p,y)else:cnt += 1p = yreturn pow(2,cnt,MOD)
五、[Hard] 2581. 统计可能的树根数目
链接: 2581. 统计可能的树根数目
1. 题目描述
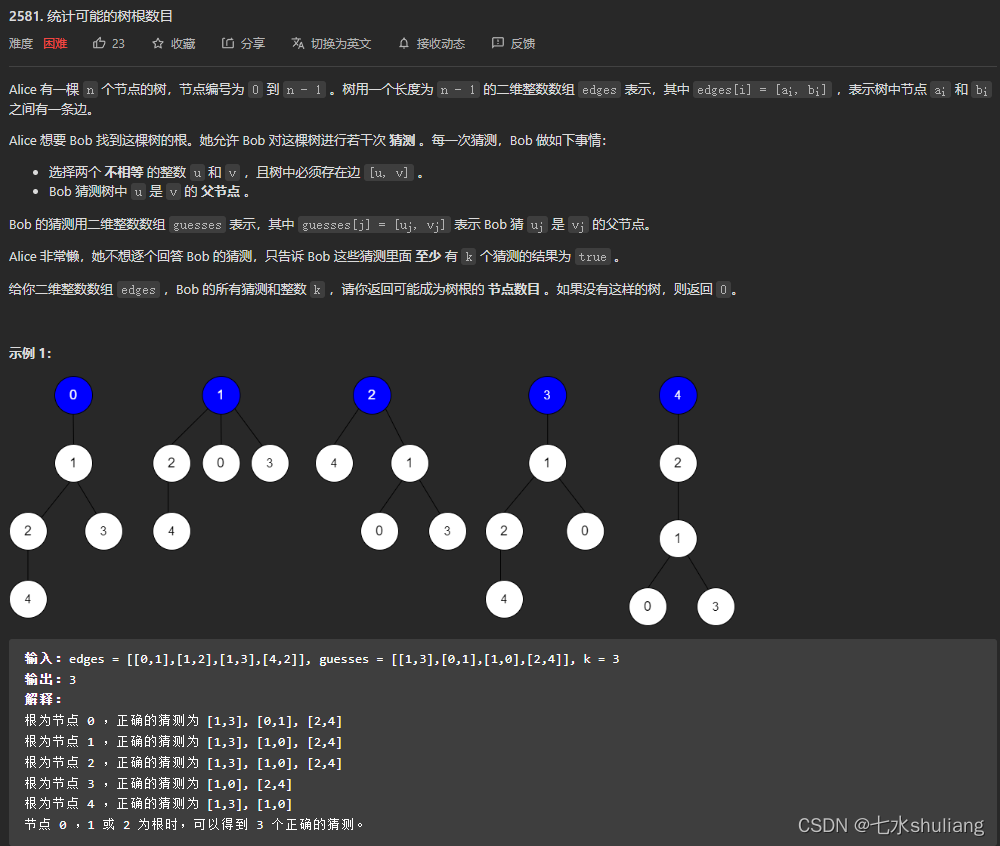
2. 思路分析
- 知道是换根DP,之前学了max版的换根dp,这次遇到加法的就不会了。
- 学了一下。
- 当然用模板也能做。
3. 代码实现
class Solution:def rootCount(self, edges: List[List[int]], guesses: List[List[int]], k: int) -> int:n = len(edges)+ 1g = [[] for _ in range(n)]for u,v in edges:g[u].append(v)g[v].append(u)s = set(tuple(x) for x in guesses)f = [0]*ndef dfs(u,fa):for v in g[u]:if v != fa:if (u,v) in s:f[0] += 1dfs(v,u)def reroot(u,fa):for v in g[u]:if v != fa:f[v] = f[u] + int((v,u) in s) - int((u,v) in s)reroot(v,u)dfs(0,-1)reroot(0,-1)return sum(x >= k for x in f)
六、参考链接
相关文章:

[LeetCode周赛复盘] 第 99 场双周赛20230304
[LeetCode周赛复盘] 第 99 场双周赛20230304 一、本周周赛总结二、 [Easy] 2578. 最小和分割1. 题目描述2. 思路分析3. 代码实现三、[Medium] 2579. 统计染色格子数1. 题目描述2. 思路分析3. 代码实现四、[Medium] 2580. 统计将重叠区间合并成组的方案数1. 题目描述2. 思路分析…...

Parcel Bundle漏洞学习
Bundle的序列化细节看上去还是有些复杂的,在之前已经讨论过,一般我们使用Parcel的时候,都是严格的write和read相对应。一些疏漏,不对应,竟然就可以成为漏洞,https://xz.aliyun.com/t/2364 里介绍了Bundle漏…...

RTP载荷H264(实战细节)
RTP包由两部分组成,RTP头和RTP载荷: RTP头 RTP头的 结构如下: 代码结构: typedef struct RtpHdr {uint8_t cc : 4, // CSRC countx : 1, // header extendp : 1, // padding flagversion : 2; // versionuint8_t …...

软考高级信息系统项目管理师系列之四十三:信息系统安全管理
软考高级信息系统项目管理师系列之四十三:信息系统安全管理 一、信息系统安全管理内容二、信息安全策略1.信息系统安全策略的概念与内容2.信息系统安全等级保护的概念三、信息安全系统1.信息安全系统三维空间2.信息安全系统三种架构体系四、PKI公开密钥基础设施1.PKI总体架构2…...
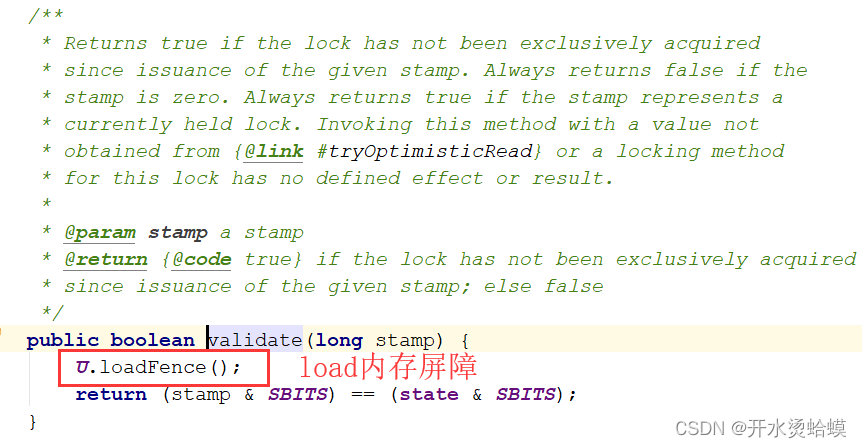
并发编程之AtomicUnsafe
目录 原子操作 定义 术语 处理器如何实现原子操作 处理器自动保证基本内存操作的原子性 使用总线锁保证原子性 使用缓存锁保证原子性 Java当中如何实现原子操作 Atomic 定义 原子更新基本类型类 原子更新数组类 原子更新引用类型 原子更新字段类 Unsafe应用解析…...
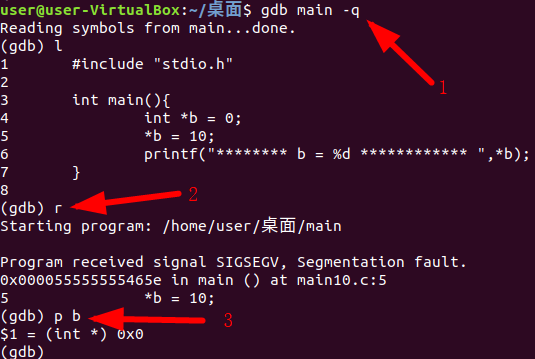
GDB调试快速入门
什么是GDB: GDB - - - (GNU symbolic debugger)是Linux平台下最常用的一款程序调试器。 自己的Linux是否安装GDB? 一般来说,使用Ubuntu的话,系统就会自带的有GDB调试器的 命令窗口输入如下命令可以查看是否安装了gdb: gdb -v …...

Vim一次复制,多次粘贴
我们平常在使用Vim时候,通过viwy或者yy等复制操作之后,p操作粘贴的时候,只能粘贴一次,想要粘贴多次怎么办? 解决方案:在使用p的是时候使用"0p,这样就能无限制的一直粘贴了。 可是ÿ…...
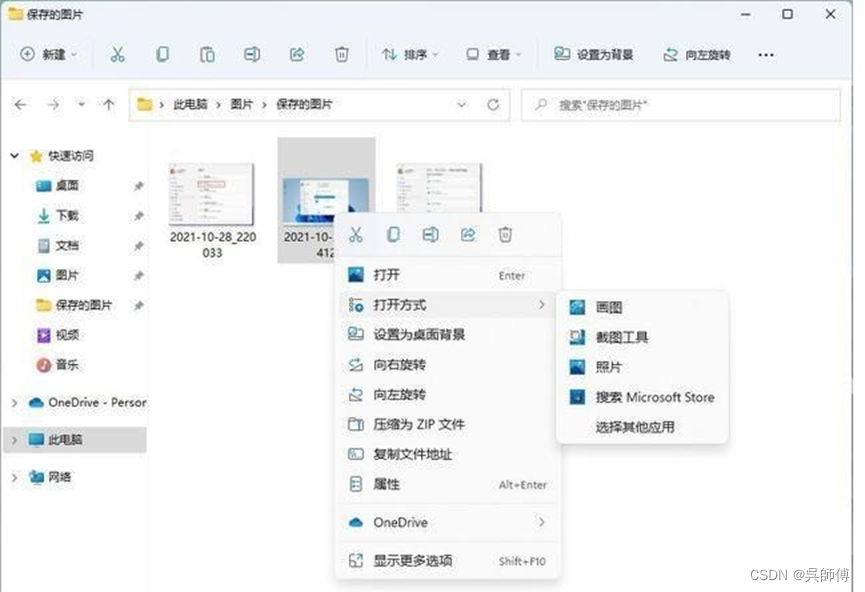
如何修改Win11上的默认程序?
在Win10之前,更改特定文件格式的默认程序很简单,但在Win11发布之后,很多用户都不清楚关于Win11的修改默认程序的操作步骤,接下来我们就一起来看看吧,希望可以帮助到大家。 步骤如下: 一、如何更改Windows 1…...
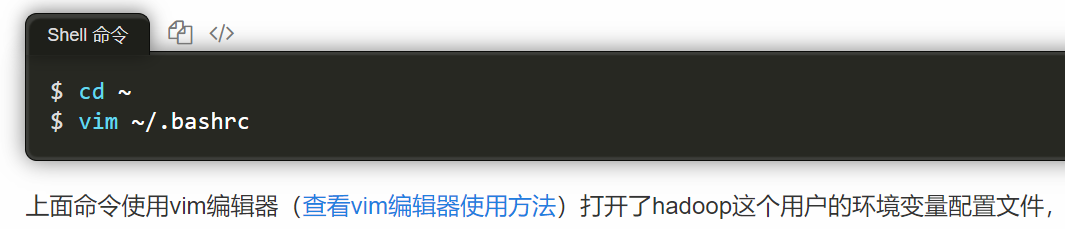
安装Linux虚拟机和Hadoop平台教程汇总及踩坑总结
📍主要内容介绍安装Linux虚拟机、ubuntu系统、安装hadoop三个环节的教程链接介绍及本机与虚拟机的FTP传输教程总结(直接找hadoop安装环节的5.filezilla传输文件)新鲜出炉的踩坑总结和填坑指南安装Linux虚拟机和ubuntu系统一、材料和工具1、下…...

Shell脚本的使用和介绍
为了方便以后工作使用和复习,吐血整理记录一下学习shell脚本的笔记,看这篇文章需要对linux系统熟悉,希望对大家有所帮助! 文章目录 目录 文章目录 一、什么是shell? 为什么要学习和使用shell? 二、shell的分类...
机械学习 - 基础概念 - scikit-learn - 数据预处理 - 1
目录安装 scikit-learn术语理解1. 特征(feature )和样本( sample / demo)的区别?2. 关于模型的概念一、机械学习概念1. 监督学习总结:2. 非监督学习总结:3. 强化学习总结:三种学习的…...
)
OLCNE cluster 配置 NFS Storage(英文)
OLCNE cluster 配置 NFS Storage(英文)Create an OLCNE cluster.Create an NFS server.a. Install the NFS utility package on the server and client instances.b. Create a directory for your shared files. Make sure that the server does not hav…...
RabbitMQ高级特性
RabbitMQ高级特性 消息可靠性投递 Consumer ACK 消费端限流 TTL 死信队列 延迟队列 日志与监控 消息可靠性分析与追踪 管理 消息可靠性投递 在使用 RabbitMQ 的时候,作为消息发送方希望杜绝任何消息丢失或者投递失败场景。RabbitMQ 为我们提供了两种方式用来控制…...
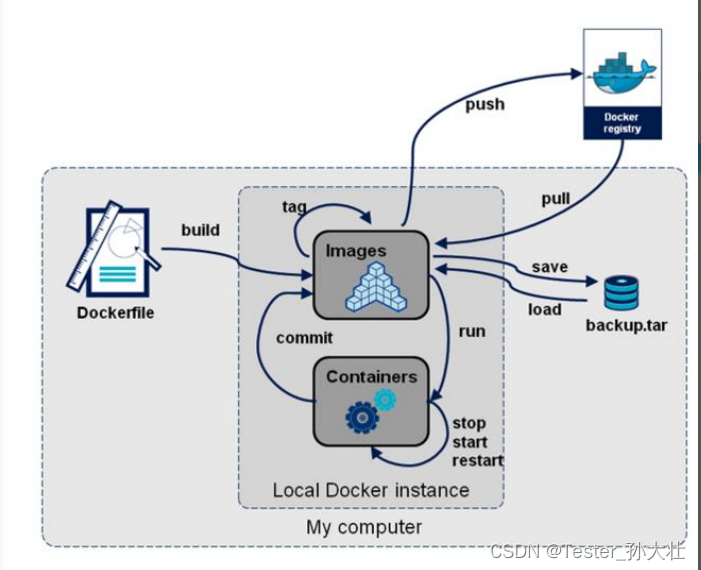
利用Dockerfile开发定制镜像实战.
Dockerfile的原理 dockerfile是一种文本格式的文件,用于描述如何构建Docker镜像。在Dockerfile中,我们可以定义基础镜像、安装依赖、添加文件等操作,最终生成一个可以直接运行的容器镜像。 Dockerfile的原理可以分为以下几个步骤:…...

PyInstaller 将DLL文件打包进exe
PyInstaller 将DLL文件打包进exe方法1:通过--add-data命令方法2:通过修改 .spec扩展:博主热门文章推荐:方法1:通过–add-data命令 注意:这里 dll末尾添加的.为当前目录,则该dll要放到main.py同一…...
【JVM篇2】垃圾回收机制
目录 一、GC的作用 申请变量的时机&销毁变量的时机 内存泄漏 内存溢出(oom) 垃圾回收的劣势 二、GC的工作过程 回收垃圾的过程 第一阶段:找垃圾/判定垃圾 方案1:基于引用计数(非Java语言) 引用计数方式的缺陷 方案2:可达性分析…...
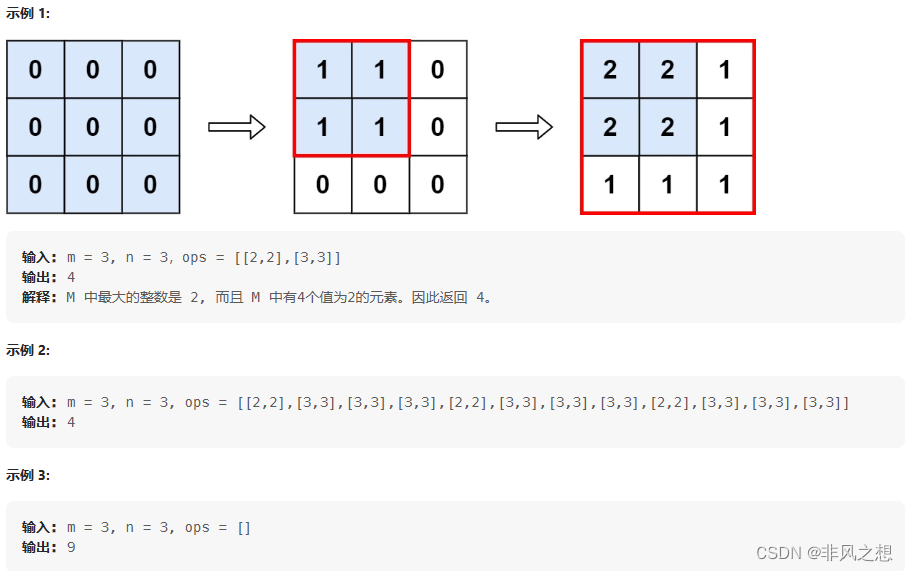
LeetCode598. 范围求和 II(python)
题目 给你一个 m x n 的矩阵 M ,初始化时所有的 0 和一个操作数组 op ,其中 ops[i] [ai, bi] 意味着当所有的 0 < x < ai 和 0 < y < bi 时, M[x][y] 应该加 1。 提示: 1 < m, n < 4 * 104 0 < ops.length < 104 o…...

观察者模式与发布订阅模式
前言 我的任督二脉终于被打通了,现在该你了 区别 观察者模式 就2个角色:观察者和被观察者(重要)明确知道状态源,明确知道对方是谁一对多关系 发布订阅模式 有3个角色:发布者,订阅者和发布订阅…...

磨金石教育摄影技能干货分享|烟花三月下扬州,是时候安排了!
人间三月最柔情,杨柳依依水波横。三月的风将要吹来,春天的门正式打开。对中国人来说,古往今来,赏春最好的地方是江南。人人都说江南好,可是江南哪里好呢?古人在这方面早就给出了答案:故人西辞黄…...

Kafka 消费组位移
Kafka 消费组位移消费者 API命令行Kafka : 基于日志结构(log-based)的消息引擎 消费消息时,只是从磁盘文件上读取数据,不会删除消息数据位移数据能由消费者控制,能很容易修改位移的值,实现重复消费历史数据…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
