PTA-线性表实验(JAVA)
题目1:Josephus环的问题及算法
【实验内容】
编程实现如下功能:
题意说明:古代某法官要判决n个犯人的死刑,他有一条荒唐的法律,将犯人站成一个圆圈,从第start个犯人开始数起,每数到第distance的犯人,就出列处决;再从下一个犯人开始计数,数到的犯人被处决……以此类推不断循环,直到剩下最后一个犯人予以赦免。此为Josephus环问题。
要求:采用线性表(可以为顺序表或链表)标记n个人,这n个人分别标为A、B、C……,请用Java语言编写程序,按顺序输出出列人的标记。
【实验要求】
输入格式:
输入为3个正整数,分别表示n、start、distance,均不超过1000
输出格式:
输出为一行整数,为出列人的编号。每个整数后一个空格。
(1)解决思路

(2)代码截图
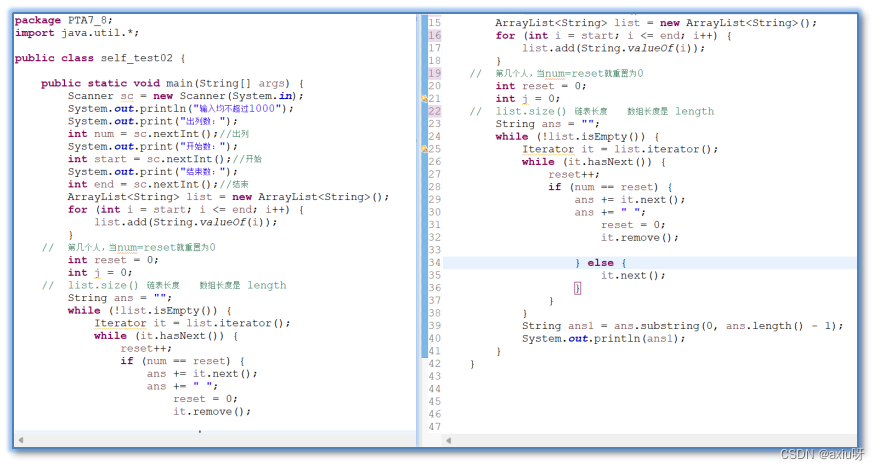
(3)源代码
import java.util.*;
public class self_test02 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);System.out.println("输入均不超过1000");System.out.print("出列数:");int num = sc.nextInt();//出列System.out.print("开始数:");int start = sc.nextInt();//开始System.out.print("结束数:");int end = sc.nextInt();//结束ArrayList<String> list = new ArrayList<String>();for (int i = start; i <= end; i++) {list.add(String.valueOf(i));}// 第几个人,当num=reset就重置为0int reset = 0;int j = 0;// list.size() 链表长度 数组长度是 lengthString ans = "";while (!list.isEmpty()) {Iterator it = list.iterator();while (it.hasNext()) {reset++;if (num == reset) {ans += it.next();ans += " ";reset = 0;it.remove();} else {it.next();}}}String ans1 = ans.substring(0, ans.length() - 1);System.out.println(ans1);}}
}(4)实验结果
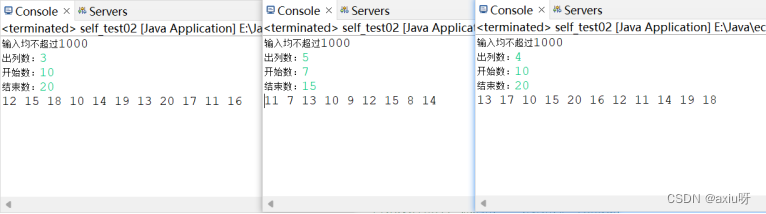
题目2:银行业务队列简单模拟
【实验内容】
设某银行有A、B两个业务窗口,且处理业务的速度不一样,其中A窗口处理速度是B窗口的2倍 —— 即当A窗口每处理完2个顾客时,B窗口处理完1个顾客。给定到达银行的顾客序列,请按业务完成的顺序输出顾客序列。假定不考虑顾客先后到达的时间间隔,并且当不同窗口同时处理完2个顾客时,A窗口顾客优先输出。
【实验要求】
输入格式:
输入为一行正整数,其中第1个数字N(≤1000)为顾客总数,后面跟着N位顾客的编号。编号为奇数的顾客需要到A窗口办理业务,为偶数的顾客则去B窗口。数字间以空格分隔。
输出格式:
按业务处理完成的顺序输出顾客的编号。数字间以空格分隔,但最后一个编号后不能有多余的空格。
输入样例:
8 2 1 3 9 4 11 13 15
输出样例:
1 3 2 9 11 4 13 15
(1)解题思路
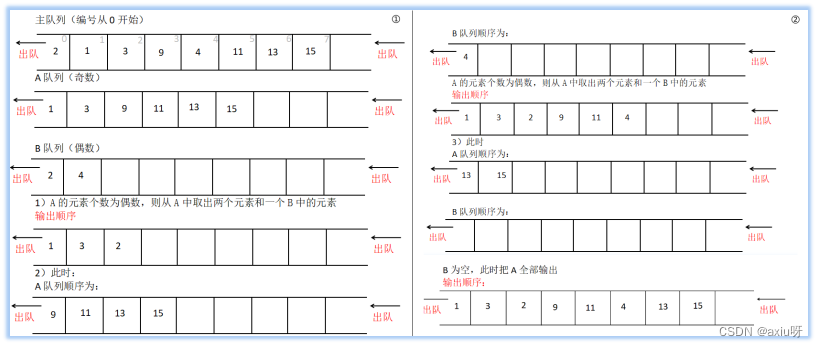
(2)代码截图

(3)源代码
import java.util.*;
public class self_test {public static void main(String[] args) {// TODO Auto-generated method stubScanner scanner = new Scanner(System.in);int num = scanner.nextInt();int[] arr = new int[num];
// 创建一个数组,用于存放所有输入值(除第一位)for (int i = 0; i < num; i++) {arr[i] = scanner.nextInt();}
// 创建a,b队列ArrayDeque arr_a = new ArrayDeque();ArrayDeque arr_b = new ArrayDeque();
// 编号为奇数的顾客需要到A窗口办理业务,为偶数的顾客则去B窗口for (int i = 0; i < arr.length; i++) {if (arr[i] % 2 == 0) {arr_b.add(arr[i]) ;} else {arr_a.add(arr[i]) ;}} String str = new String();while(!arr_a.isEmpty() && !arr_b.isEmpty()) {
// A的元素个数为偶数,则从A中取出两个元素和一个B中的元素if (arr_a.size() % 2 ==0) {str += arr_a.removeFirst()+" ";str += arr_a.removeFirst()+" ";str += arr_b.removeFirst()+" ";}else {
// A的元素个数为奇数,则从A中取出一个元素和一个B中的元素str += arr_a.removeFirst()+" ";str += arr_b.removeFirst()+" ";}}
// A为空时,把B的元素赋值给Aif (arr_a.isEmpty()) {arr_a = arr_b;}
// 将A中的所有元素取出,依次将它们拼接成一个字符串if (!arr_a.isEmpty()) {while(!arr_a.isEmpty()) {str+=arr_a.removeFirst()+" ";}}
// 去掉最后一个空格System.out.println(str);}
}
(4)运行结果
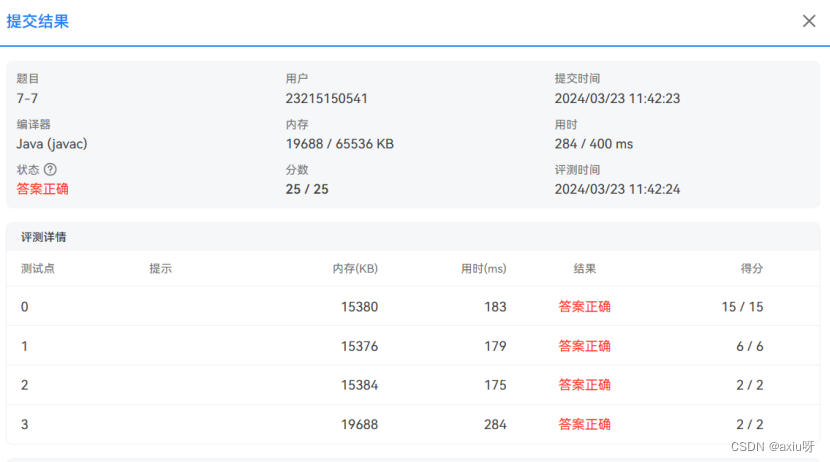
相关文章:

PTA-线性表实验(JAVA)
题目1:Josephus环的问题及算法 【实验内容】 编程实现如下功能: 题意说明:古代某法官要判决n个犯人的死刑,他有一条荒唐的法律,将犯人站成一个圆圈,从第start个犯人开始数起,每数到第distance的…...

LeetCode:494. 目标和
题目 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添…...

HarmonyOS Next开发学习手册——选项卡 (Tabs)
当页面信息较多时,为了让用户能够聚焦于当前显示的内容,需要对页面内容进行分类,提高页面空间利用率。 Tabs 组件可以在一个页面内快速实现视图内容的切换,一方面提升查找信息的效率,另一方面精简用户单次获取到的信息…...

LeetCode2710.移除字符串中的尾随零
cpp class Solution { public:string removeTrailingZeros(string num) {int flag 0;string s num;int size num.length();for (int i num.length() - 1; i > 0; i--) {if (num[i] ! 0)break;if (num[i] 0) {size--;}}s.resize(size);return s;} };...
PPT录屏怎么录?PPT录屏,3种方法简单操作
在数字化时代,PPT已经成为我们日常工作、学习和生活中不可或缺的一部分。无论是商务报告、教学课件还是产品展示,PPT都能帮助我们更加生动、直观地传递信息。然而,有时候我们会面临PPT录屏怎么录的问题。这时,一个好的PPT录屏功能…...

HarmonyOS开发:应用完整性校验
简介 为了确保应用的完整性和来源可靠,OpenHarmony需要对应用进行签名和验签。 应用开发阶段: 开发者完成开发并生成安装包后,需要开发者对安装包进行签名,以证明安装包发布到设备的过程中没有被篡改。OpenHarmony的应用完整性校…...

【MySQL基础篇】SQL指令:DQL及DCL
1、DQL DQL - 介绍 DQL英文全称是Data Query Language(数据查询语言),数据查询语言,用来查询数据表中的记录。(在MySQL中应用是最为广泛的) 查询关键字:SELECT DQL - 语法 SELECT 字段列表 FROM 表名列表 WHER…...
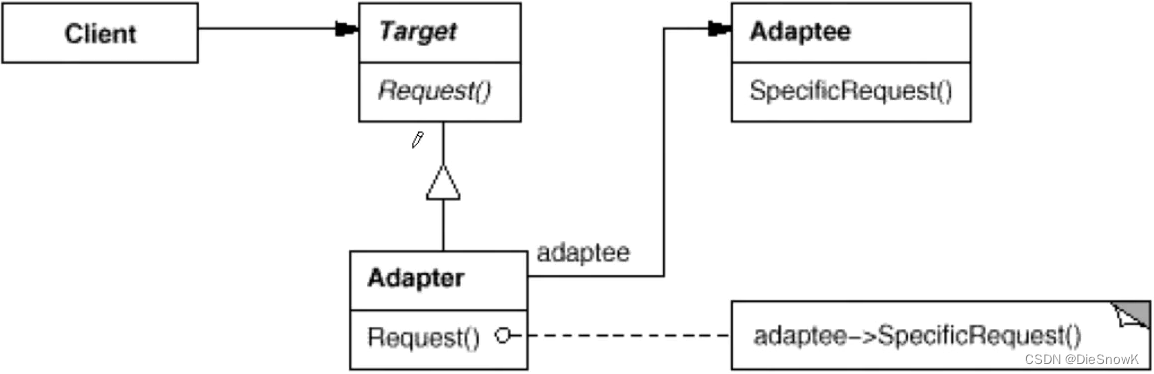
[C++][设计模式][适配器模式]详细讲解
目录 1.动机2.模式定义3.要点总结4.代码感受 1.动机 在软件系统中,由于应用环境的变化,常常需要将”一些现存的对象“放在新的环境中应用,但是新环境要求的接口是这些现存对象所不满足如何应对这些”迁移的变化“?如何既能利用现…...

8080时序驱动TFT显示屏 驱动IC GC9307
8080时序总共有控制线 CS片选线 DC(命令数据控制线) RD读控制线 WR写控制线 和N条数据线。 控制底层代码如下; 写读代码,读的代码反过来就行 inline void TFT8080WriteDat(unsigned char dat) {CS_L;//开始片选DC_H;//写数据 // RD_H;//禁止读WR_H;//禁止写WR_L;//写入…...

K8S 集群节点缩容
环境说明: 主机名IP地址CPU/内存角色K8S版本Docker版本k8s231192.168.99.2312C4Gmaster1.23.1720.10.24k8s232192.168.99.2322C4Gwoker1.23.1720.10.24k8s233(需下线)192.168.99.2332C4Gwoker1.23.1720.10.24 1. K8S 集群节点缩容 当集群中有…...

Web-HTML-事件
1 需求 2 语法 3 示例 4 参考资料 HTML 事件 | 菜鸟教程...
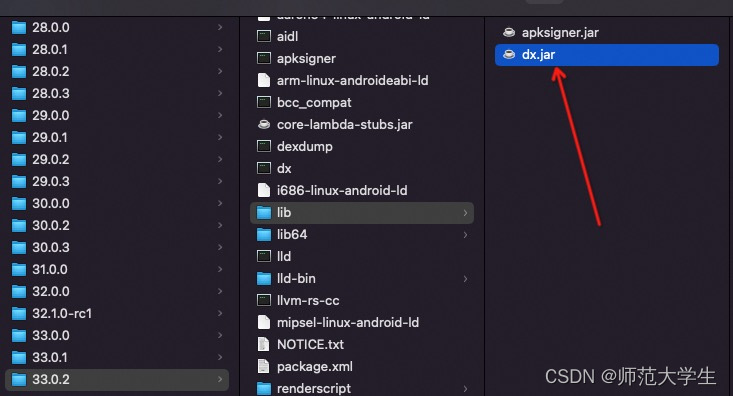
Installed Build Tools revision xxx is corrupted. Remove and install again 解决
1.在buildTools文件下找到对应的sdk版本,首先将版本对应目录下的d8.bat改名为dx.bat。 2.在lib文件下将d8.jar改名为dx.jar。 3.重新编译工程即可...

AI 与 Python 实战干货:基于深度学习的图像识别
《AI 与 Python 实战干货:基于深度学习的图像识别》 今天咱不啰嗦,直接上干货! 在 AI 领域,特别是图像识别方面,Python 简直是一把利器。咱就以手写数字识别为例,来看看怎么用 Python 实现一个深度学习模…...

万字长文详解数据结构:树 | 第6章 | Java版大话数据结构 | 二叉树 | 哈夫曼树 | 二叉树遍历 | 构造二叉树 | LeetCode练习
📌本篇分享的大话数据结构中🎄树🎄这一章的知识点,在此基础上,增加了练习题帮助大家理解一些重要的概念✅;同时,由于原文使用的C语言代码,不利于学习Java语言的同学实践,…...
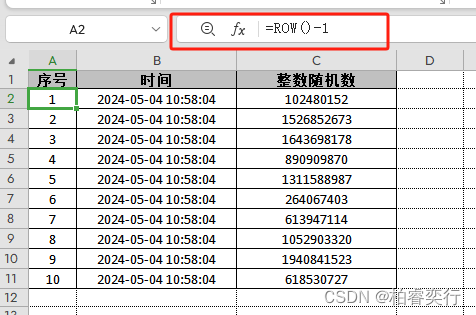
NPOI入门指南:轻松操作Excel文件的.NET库
目录 引言 一、NPOI概述 二、NPOI的主要用途 三、安装NPOI库 四、NPOI基本使用 六、性能优化和内存管理 七、常见问题与解决方案 八、结论 附录 引言 Excel文件作为数据处理的重要工具,广泛应用于各种场景。然而,在没有安装Microsoft Office的…...
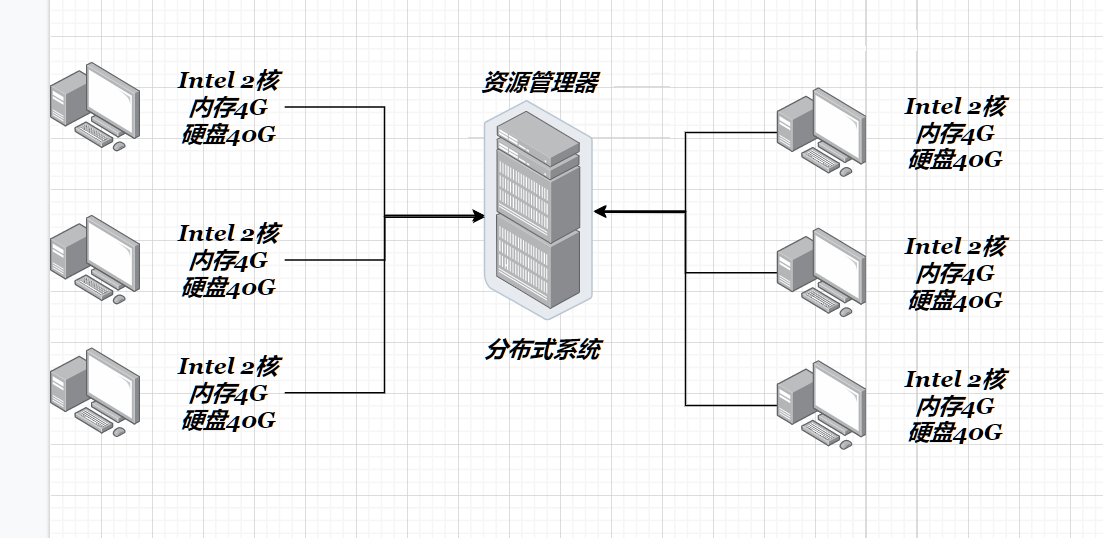
【高性能服务器】服务器概述
🔥博客主页: 我要成为C领域大神🎥系列专栏:【C核心编程】 【计算机网络】 【Linux编程】 【操作系统】 ❤️感谢大家点赞👍收藏⭐评论✍️ 本博客致力于知识分享,与更多的人进行学习交流 服务器概述 服…...

003 SSM框架整合
文章目录 整合web.xmlapplicationContext-dao.xmlapplicationContext-service.xmlspringmvc.xmldb.propertieslog4j.propertiespom.xml 测试sqlItemController.javaItemMapper.javaItem.javaItemExample.javaItemService.javaItemServiceImpl.javaItemMapper.xml 整合 将工程的…...
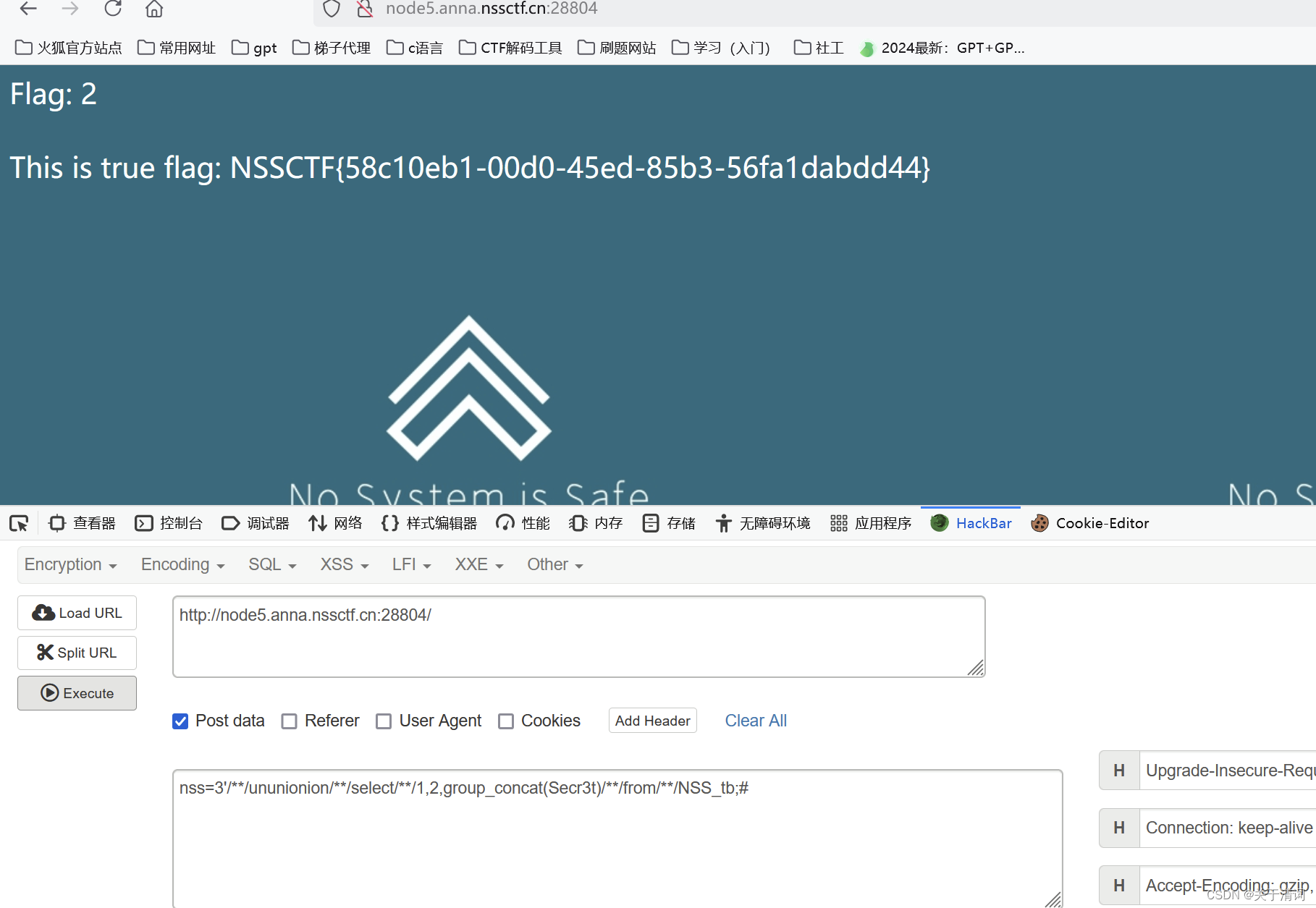
web刷题记录(7)
[HDCTF 2023]SearchMaster 打开环境,首先的提示信息就是告诉我们,可以用post传参的方式来传入参数data 首先考虑的还是rce,但是这里发现,不管输入那种命令,它都会直接显示在中间的那一小行里面,而实际的命令…...
【单片机毕业设计选题24037】-基于STM32的电力系统电力参数无线监控系统
系统功能: 系统上电后,OLED显示“欢迎使用电力监控系统请稍后”,两秒后显示“Waiting..”等待ESP8266初始化完成, ESP8266初始化成功后进入正常页面显示, 第一行显示电压值(单位V) 第二行显示电流值&am…...

Python使用彩虹表来尝试对MD5哈希进行破解
MD5是一种散列算法,它是不可逆的,无法直接解密。它的主要作用是将输入数据进行散列,生成一个固定长度的唯一哈希值。 然而,可以使用预先计算好的MD5哈希值的彩虹表(Rainbow Table)来尝试对MD5进行破解。彩…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
