秋招突击——6/28、6.29——复习{数位DP——度的数量}——新作{}
文章目录
- 引言
- 复习
- 数位DP——度的数量
- 个人实现
- 参考实现
- 总结
引言
- 头一次产生了那么强烈的动摇,对于未来没有任何的感觉的,不知道将会往哪里走,不知道怎么办。可能还是因为实习吧,再加上最近复习也没有什么进展,并不知道该怎么办,投的提前批基本上没什么回应,投的实习基本上都挂了。
- 在加上不在学校,没有办法和同学一块共享信息,一个人总是觉得有点孤零零的,难受,并且是忧郁的。
- 想那么多也没用,还是得继续复习。按照我的计划来。
- 上午出去有事,基本上没有刷算法,下午才开始刷算法。
复习
数位DP——度的数量

- 这一类题型之前基本上都没有做过,现在得好好补充一下,感觉听名字和状态压缩DP很像。
注意
- X和Y是区间长度,是INT类型的数字的上限,并且只能是正数
- 左右区间的都是闭合的,所以临界条件是两边相等,仅仅只有一个数字。
个人实现
- 首先,这里得先解决一个数字,才能解决所有的数字,所以得先专注于解决一个数字的判定。
- 这里是B的整数次幂,所以可以想成若干进制去思考,之前应该做过类似的出发是一个思路,肯定是能够先用高次幂的结果进行表示,然后再用低次幂的结果进行表示。然后在判定这个数字能否用一个较低位进行表示,这道题就算是结束了。
#include <iostream>
#include <vector>using namespace std;int x,y,k,b;
vector<int> exp;int main(){cin>>x>>y;cin>>k>>b;// 保存b的不同次幂的中间结果int res = 0;int i=1;exp.push_back(1);for ( i = b; i <= y ; i *= b)exp.push_back(i);for (int i = x; i <= y; ++i) {// 判断每一个数字是否能够使用对应的数字进行保存int cnt = k,temp = i;for (int j = exp.size() - 1; j >= 0 ; j --) {if (exp[j] <= temp){temp -= exp[j];cnt --;if (cnt >= 0 ){if (cnt == 0 && temp == 0)res ++;}elsebreak;}}}cout<<res;
}
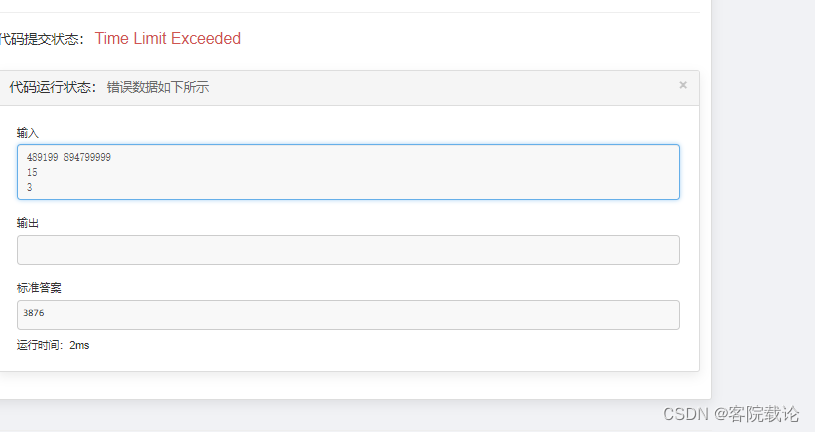
实验结果如下
- 我的时间复杂度太高了,遍历所有的数字,然后在遍历每一个数字,看看能否出现对应的结果。相当于使(y - x) * k相当远的平方的运算时间复杂度。
参考实现
- 这里应该是使用了数位DP,之前并没有学过。
数位DP的相关技巧
- 区间转成边界相减问题:
- 计算的区间【X,Y】中所有符合条件的数字,使用1到Y的所有符合条件的数字的数量,减去1到X中所有符合条件的数字的数量。【X,Y】 = f(Y) - f(X - 1)
- 从树的角度去考虑数位DP问题
- 对于每一个数字的位数,只有两种情况,就是加入对应的分支以及不加入对应的分支等。
这里完全跳过了,看不懂,大约花了差不多一个小时,视频讲解有问题在加上题目的难度比较大,以后调整自己的复习思路,不在学习这种难度较高的算法题,主要还是刷对应的笔试题库
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 35;int l, r, k, b;
int a[N], al;
int f[N][N];int dp(int pos, int st, int op) //op: 1=,0<
{//枚举到最后一位数位,是否恰有k个不同的1(也是递归的终止条件)if (!pos) return st == k;//记忆化搜索,前提是不贴着上界(可以枚举满这一位所有的数字)if (!op && ~f[pos][st]) return f[pos][st];//01数位dp,贴着上界时,本轮能枚举的最大数就是上界数位的数字和1之间的最小值int res = 0, maxx = op ? min(a[pos], 1) : 1;for (int i = 0; i <= maxx; i ++ ){if (st + i > k) continue;res += dp(pos - 1, st + i, op && i == a[pos]);}return op ? res : f[pos][st] = res;
}
int calc(int x)
{al = 0; memset(f, -1, sizeof f); //模板的必要初始化步骤while (x) a[ ++ al] = x % b, x /= b; //把x按照进制分解到数组中return dp(al, 0, 1);
}
int main()
{cin >> l >> r >> k >> b;cout << calc(r) - calc(l - 1) << endl;return 0;
}
作者:一只野生彩色铅笔
链接:https://www.acwing.com/solution/content/66855/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
总结
-
明天朋友来家里做客,忙完这一阵之后,就闭门谢客,专心好好准备秋招。马上第一批就开始了,但是我的项目还是没有准备好,进度太慢了,不行的。
-
我就在想,我真的有必要刷这么多算法进阶题目吗?今天的数位DP好难呀,感觉要花一上午,不如多花点时间去做热搜题目的一百道题。感觉到此为止了,不想再花时间去做这写题目了,数位DP太难了,根本就不会做。讲的有问题。
-
不想浪费时间了,单纯的针对一百热题吧,不在刷什么难题了,只能用题库堆起来,然后如果有不会的题目,再去看他的讲解,不能在这样往下跟了,然后每天上午的题目,就是单纯复习现在已经学到的相关算法了。 我是找工作的,不是面对算法竞赛的。
-
大概看了一下,就课程安排来说,虽然刷的是leetcode,但是还是会提到对应的题型进行讲解,所以转变以下自己的思路,不然这样化的时间实在太多了,完全没有必要。
-
而且我大概看了一下,基本上我在面试中遇到的问题,在这里基本上都能遇见,在腾讯面试中遇见的使用LRU,然后华为面试中遇见的三数之和等等。还是调整一下重点,重点围绕以下两个课题,分别是
- leetcode热题100道
- 面试经典150道
-
差不多一天三到四道题,差不多一个月刷一遍,还能回顾一遍。不要浪费时间。
相关文章:

秋招突击——6/28、6.29——复习{数位DP——度的数量}——新作{}
文章目录 引言复习数位DP——度的数量个人实现参考实现 总结 引言 头一次产生了那么强烈的动摇,对于未来没有任何的感觉的,不知道将会往哪里走,不知道怎么办。可能还是因为实习吧,再加上最近复习也没有什么进展,并不知…...

Spring Boot中使用Thymeleaf进行页面渲染
Spring Boot中使用Thymeleaf进行页面渲染 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Spring Boot应用中使用Thymeleaf模板引擎进行页面…...

恢复策略(下)-事务故障后的数据库恢复、系统故障后的数据库恢复(检查点技术)、介质故障后的数据库恢复
一、数据库恢复-事务故障 系统通过对事物进行UNDO操作和REDO操作可实现故障后的数据库状态恢复 1、对于发生事务故障后的数据库恢复 恢复机制在不影响其他事务运行的情况下,强行回滚夭折事务,对该事务进行UNDO操作,来撤销该事务已对数据库…...

如何知道docker谁占用的显卡的显存?
文章目录 python环境安装nvidia-htop查看pid加一个追踪总结一下【找到容器创建时间】使用说明示例 再总结一下【用PID找到容器创建时间,从而找到谁创建的】使用说明示例 python环境安装nvidia-htop nvidia-htop是一个看详细的工具。 pip3 install nvidia-htop查看…...
wps linux node.js 加载项开发,和离线部署方案
环境准备 windwos 安装node.js 安装VSCode 安装wps linux 安装node.js 安装VSCode 安装wps 通过npm 安装wpsjs SDK 使用npm安装wpsjs npm install -g wpsjs 创建一个项目 wpsjs create WPS-Addin-PPT 创建项目会让你选择2个东西: 1:选择你的文…...
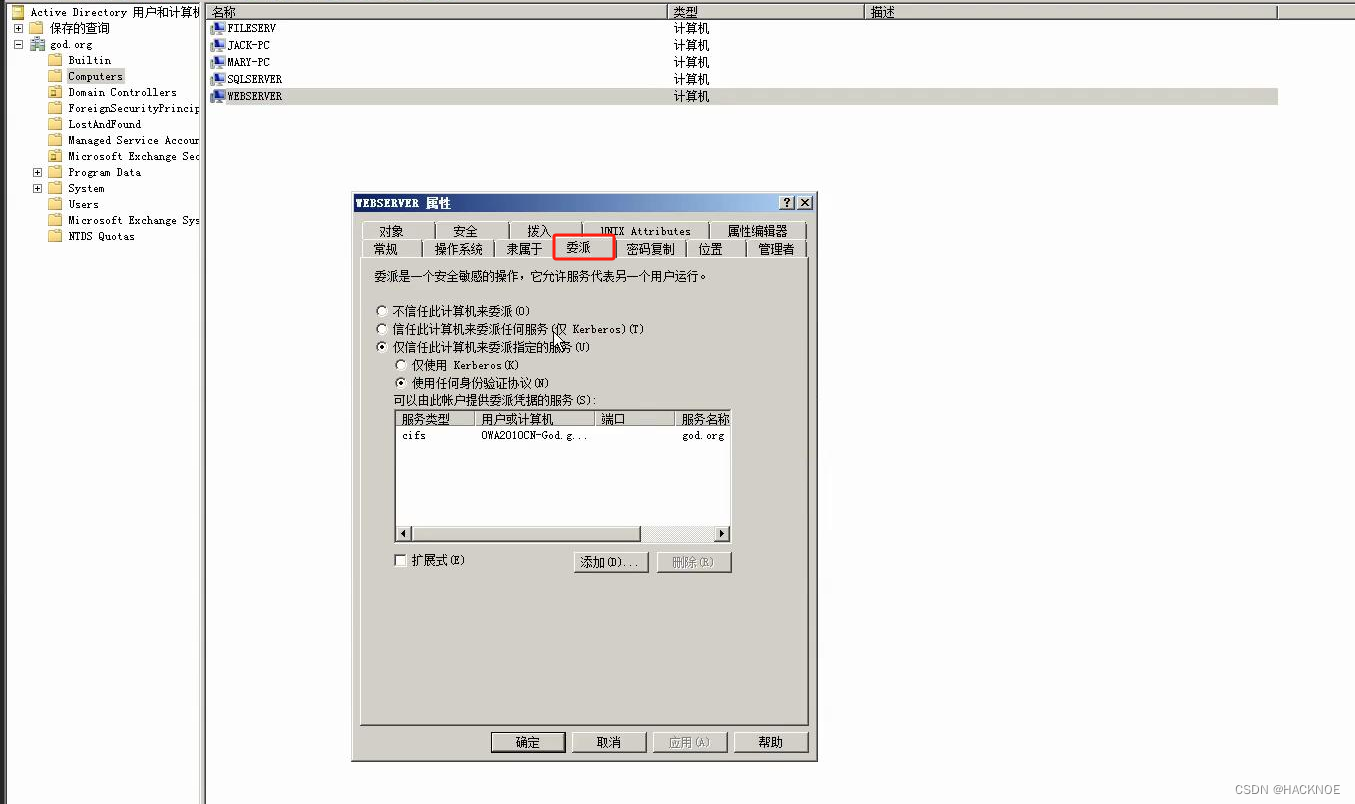
红队内网攻防渗透:内网渗透之内网对抗:横向移动篇Kerberos委派安全非约束系约束系RBCD资源系Spooler利用
红队内网攻防渗透 1. 内网横向移动1.1 委派安全知识点1.1.1 域委派分类1.1.2 非约束委派1.1.2.1 利用场景1.1.2.2 复现配置:1.1.2.3 利用思路1:诱使域管理员访问机器1.1.2.3.1 利用过程:主动通讯1.1.2.3.2 利用过程:钓鱼1.1.2.4 利用思路2:强制结合打印机漏洞1.1.2.5 利用…...

nginx上传文件限制
默认限制 Nginx 限制文件大小可以通过 client_max_body_size 指令来设置,该指令通常在 http、server 或 location 块中设置,如果不设置,默认上传大小为1M。 修改上传文件限制 要修改Nginx的文件上传大小限制,你需要编辑Nginx的配…...

76. 最小覆盖子串(困难)
76. 最小覆盖子串 1. 题目描述2.详细题解3.代码实现3.1 Python3.2 Java 1. 题目描述 题目中转:76. 最小覆盖子串 2.详细题解 在s中寻找一个最短的子串,使之包含t中的所有字符,t中可能存在多个相同字符,寻找的子串也应至少含有…...

K8S 集群节点扩容
环境说明: 主机名IP地址CPU/内存角色K8S版本Docker版本k8s231192.168.99.2312C4Gmaster1.23.1720.10.24k8s232192.168.99.2322C4Gwoker1.23.1720.10.24k8s233(需上线)192.168.99.2332C4Gwoker1.23.1720.10.24 当现有集群中的节点资源不够用&…...
AI大模型技术在音乐创造的应用前景
大模型技术在音乐创作领域具有广阔的应用前景,可以为音乐家、作曲家和音乐爱好者提供以下方面的帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 音乐创作辅助:大模型可以帮助音乐家和作曲家生成旋律、和声…...
Linux多进程和多线程(一)-进程的概念和创建
进程 进程的概念进程的特点如下进程和程序的区别LINUX进程管理 getpid()getppid() 进程的地址空间虚拟地址和物理地址进程状态管理进程相关命令 ps toppstreekill 进程的创建 并发和并行fork() 父子进程执行不同的任务创建多个进程 进程的退出 exit()和_exit() exit()函数让当…...

熊猫烧香是什么?
熊猫烧香(Worm.WhBoy.cw)是一种由李俊制作的电脑病毒,于2006年底至2007年初在互联网上大规模爆发。这个病毒因其感染后的系统可执行文件图标会变成熊猫举着三根香的模样而得名。熊猫烧香病毒具有自动传播、自动感染硬盘的能力,以及…...

使用Vue3和Tailwind CSS快速搭建响应式布局
### 第一部分:初始化Vue3项目并安装Tailwind CSS 首先,在你的开发环境中打开终端,然后通过Vue CLI来创建一个新的Vue3项目。输入如下命令: vue create my-vue-app 按照提示选择Vue3的相关选项,创建完毕后࿰…...
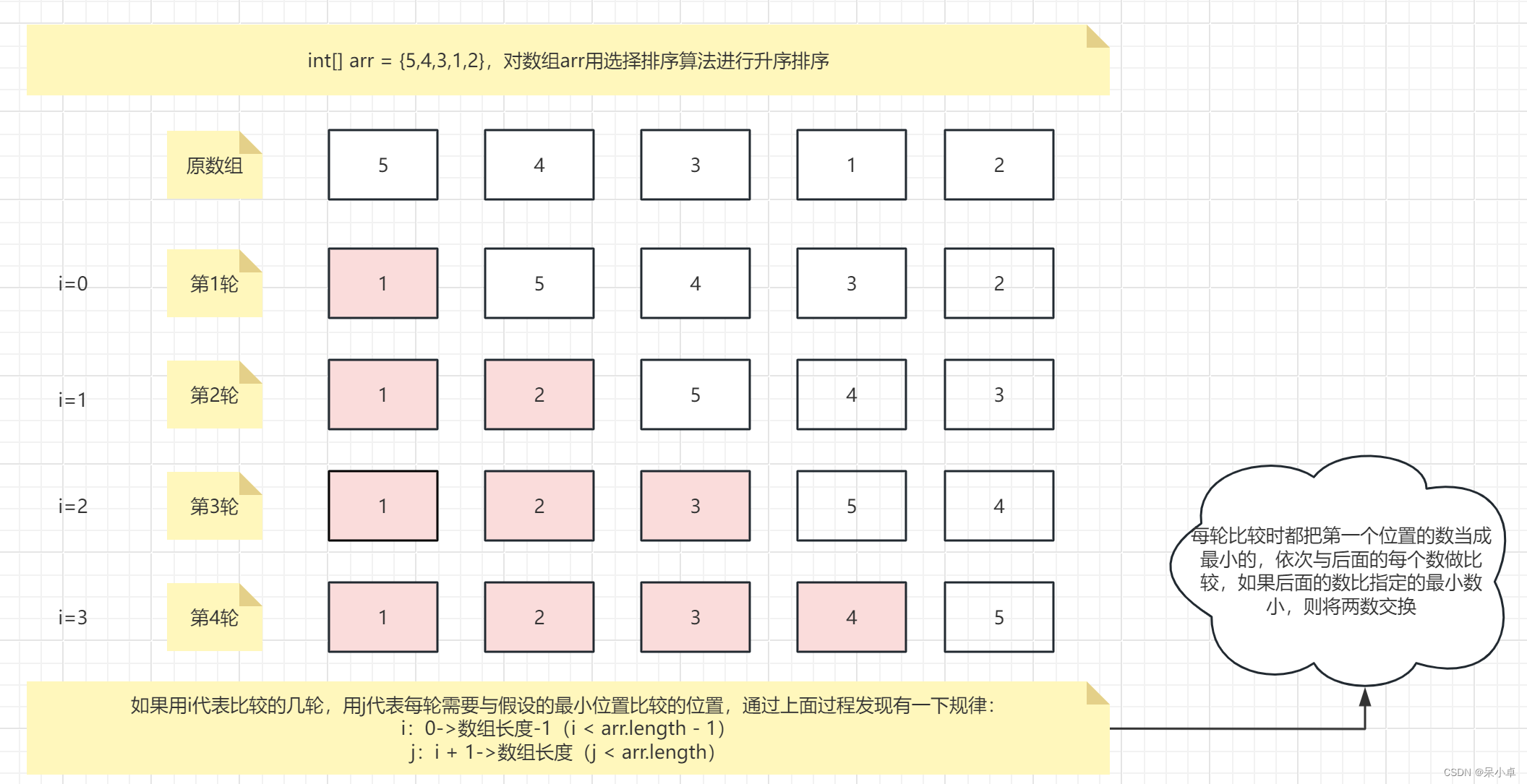
J019_选择排序
一、排序算法 排序过程和排序原理如下图所示: 二、代码实现 package com.itheima.sort;import java.util.Arrays;public class SelectSort {public static void main(String[] args) {int[] arr {5, 4, 3, 1, 2};//选择排序for (int i 0; i < arr.length - 1…...

【linux】vim的使用
目录 一、Vim的基本模式 二、Vim的常见命令 三、Vim的高级用法 四、Vim的进阶使用技巧 在Linux系统中,Vim是一款功能强大的文本编辑器,特别适用于程序员的代码编辑和修改。以下是Vim的详细使用教程,包括其基本模式、常见命令和高级用法。…...

【工具测评】ONLYOFFICE8.1版本桌面编辑器测评:好用!
随着远程工作的普及和数字化办公的发展,越来越多的人开始寻找功能强大、易于使用的办公软件。在这个背景下,ONLYOFFICE 8.1应运而生,成为许多用户的新选择。ONLYOFFICE 8.1是一款办公套件软件,提供文档处理、电子表格和幻灯片制作…...
核方法总结(四)——高斯过程回归学习笔记
一、定义 基于核方法的线性回归模型和传统线性回归一样,可以用未知数据进行预测,但不能确定 预测的可信度。在参考书第二章中可知,基于贝叶斯方法可以实现对未知数据依概率预测,进而可得到预测的可信度。这一方法中,通…...

【Python3的内置函数和使用方法】
目录 Python 特点 Python 中文编码 Python 变量类型 Python列表 Python 元组 元组是另一个数据类型,类似于 List(列表) Python 字典 Python数据类型转换 Python 运算符 Python算术运算符 Python比较运算符 Python赋值运算符 Pyt…...

递推算法计算信号特征
在线算法(在线计算或递推计算)能够在不存储全部数据的情况下逐步更新信号的特征信息,非常适合资源受限的单片机应用场景。 用途:单片机边采集ADC边计算,最终将采集的信号特征计算结果…...

spring-boot-configuration-processor注释处理器
开源项目SDK:https://github.com/mingyang66/spring-parent 个人文档:https://mingyang66.github.io/raccoon-docs/#/ spring-boot-configuration-processor是springboot提供的一个注释处理器(annotation processor),它用于在编译…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

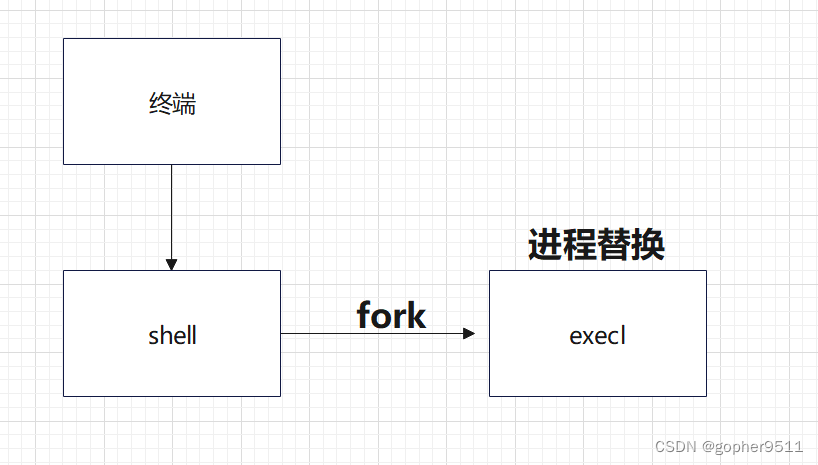
Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
