考研复试——概率论
文章目录
- 概率论
- 1. 大数定律
- 2. 中心极限定理
- 3. 大数定律和中心极限定理的区别?
- 4. 最大似然估计
- 5. 古典概型
- 6. 几何概型
- 7. 全概率公式
- 8. 贝叶斯公式
- 9. 先验概率、后验概率
- 10. 数学期望
因为初试考的数二,没有学概率论,要从头学习时间也不够,只能先整理一些重要的概念,希望能应对面试的问答。
概率论
1. 大数定律
大数定律(Law of Large Numbers)是概率论中的一组定理,它描述了随机事件重复试验的平均结果将趋近于事件的期望值。简单来说,当试验次数无限增大时,随机事件的平均值趋近于其期望值。
大数定律是统计学和概率论中最基本的定理之一,它有两种不同的形式:弱大数定律和强大数定律。
弱大数定律(也称为大数定理)表明,对于任意的正数ε,当试验次数足够大时,样本均值与总体均值之差的绝对值小于ε的概率趋近于1,即:
P(|(X1+X2+…+Xn)/n-μ| < ε) → 1 (n → ∞)
其中,X1, X2, …, Xn是n次独立重复试验的随机变量,μ是它们的期望值。
强大数定律表明,当试验次数足够大时,样本均值几乎肯定会收敛于总体均值,即:
P((X1+X2+…+Xn)/n → μ) = 1 (n → ∞)
大数定律在实际应用中非常重要,因为它保证了在大量试验中,样本的平均值会趋近于总体的平均值。这是许多领域,例如统计学、金融、天气预报等的基础。
- 例子:
一个经典的应用例子是掷硬币。如果你掷一枚公平硬币,每次正反面的概率都是50%,如果你掷了1000次硬币,根据大数定律,正面朝上的频率会趋近于50%。如果你掷了10000次硬币,正面朝上的频率会更加接近50%。
这个例子说明了大数定律的应用。虽然每次掷硬币的结果是随机的,但是当掷的次数越来越多时,我们能够得到一个更加准确的结果,这是因为大数定律的效应。在现实生活中,大数定律也被应用于统计调查、财务分析、股票市场等领域。
2. 中心极限定理
中心极限定理是统计学中最为重要的定理之一,它描述了一种现象:当一组独立随机变量相互作用时,它们的平均值会呈现出高斯分布(也被称为正态分布)。
简单来说,中心极限定理告诉我们,如果我们随机选择一组具有相同分布的随机变量,并计算它们的平均值,那么当样本数量越来越大时,这些平均值的分布将越来越接近正态分布。
这个定理的重要性在于它适用于许多不同的情况,而不必考虑原始数据分布的形式。因此,中心极限定理是许多统计分析和机器学习算法的基础。例如,它可以用来估计样本的均值和标准差,检验假设和计算置信区间等。
- 例子:
当你对一个人进行多次独立的测量时,由于个体差异等原因,这些测量值通常不完全相同。但是,根据中心极限定理,如果你对这些测量值取平均数,当测量次数足够多时,这些平均值会接近于一个正态分布,这个正态分布的均值和方差可以通过样本数据的均值和方差来计算。
举个例子,假设你要测量某人的身高。你在不同的时间和不同的地点对这个人进行多次测量,得到一系列身高值。然后,你计算这些身高值的平均值,得到一个样本平均身高值。根据中心极限定理,当你进行足够多次这样的测量和计算时,这些样本平均身高值将接近于一个正态分布,这个正态分布的均值和方差可以通过样本数据的均值和方差来计算。这个结果可以用来推断这个人的真实身高范围,并且可以在很大程度上消除由于不同测量方法、不同测量时间和地点等因素带来的误差。
3. 大数定律和中心极限定理的区别?
大数定律(Law of Large Numbers)和中心极限定理(Central Limit Theorem)是概率论中非常重要的两个定理,它们都涉及到随机变量的分布。
大数定律描述的是一个随机变量序列的样本平均值会随着样本量的增加而趋向于该随机变量的期望值。换句话说,大数定律告诉我们,当样本数量足够大时,样本平均值与总体期望值非常接近。例如,如果我们反复抛一枚硬币,那么当我们抛掷的次数足够多时,正面朝上的概率会趋近于1/2。
中心极限定理描述的是,当随机变量数量很大时,这些随机变量的均值的分布将趋近于一个正态分布。换句话说,中心极限定理告诉我们,随机变量的总体分布并不影响它们的均值分布。例如,如果我们反复抛很多次硬币,然后计算它们正面朝上的数量,这些数量的分布将会趋向于一个正态分布。
因此,大数定律和中心极限定理都是关于随机变量序列的极限行为的定理,但是它们涉及到的方面略有不同。大数定律告诉我们随着样本量的增加,样本均值会趋向于总体期望值;而中心极限定理则告诉我们,随着随机变量数量的增加,它们的均值的分布会趋向于正态分布。
4. 最大似然估计
最大似然估计是一种用于确定参数值的方法,这些参数是给定一组观测值下生成数据的分布的参数。最大似然估计的目标是找到一个参数的值,使得给定观测值下似然函数的值最大化。
最大似然估计的目的是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
似然函数是一个关于参数的函数,它度量给定参数下生成观测值的概率。最大似然估计的思想是找到一个参数的值,使得这个参数能够最大化观测到的数据集的似然函数。这个过程可以看作是在参数空间中寻找一个峰值,使得在这个峰值处,数据集的似然函数最大。
最大似然估计是一种广泛应用于统计学、机器学习和其他领域的方法。它可以用来估计各种参数,例如均值、方差、回归系数等。最大似然估计是一种无偏估计方法,当样本容量趋近于无限大时,它会收敛到真实参数的值。
- 例子:
假设你想要估计一个硬币正面向上的概率 p,但你不知道 p 的确切值。你可以通过进行多次投掷硬币来观测结果来获得信息。
假设你投掷硬币 n 次,得到 m 次正面向上的结果。我们可以用二项分布来描述这个过程,其中投掷硬币 n 次,正面向上的概率是 p,得到 m 次正面向上的结果的概率是:
P(m; n, p) = (n choose m) * p^m * (1-p)^(n-m)
其中 (n choose m) 表示从 n 次投掷中选择 m 次正面向上的组合数。这个概率可以看作是在给定 p 的情况下,得到观测数据的概率。
最大似然估计的目标是找到一个 p 的值,使得在给定观测数据下的概率最大化。我们可以把这个问题转化为寻找一个 p 的值,使得似然函数 L§ 最大化。这个似然函数可以写成:
L(p | m, n) = P(m; n, p) = (n choose m) * p^m * (1-p)^(n-m)
最大似然估计的目标是找到最大化似然函数的 p 的值。我们可以通过求似然函数的导数来找到似然函数的最大值。在这种情况下,我们可以通过求似然函数的对数并对其求导来简化问题:
ln L(p | m, n) = ln( (n choose m) * p^m * (1-p)^(n-m) ) = ln(n choose m) + m*ln§ + (n-m)*ln(1-p)
对 ln L(p | m, n) 求导,并令其等于 0,可以得到最大似然估计下的 p 的值为:
p = m/n
也就是说,在这种情况下,我们可以用观测数据的比例来估计硬币正面向上的概率。
5. 古典概型
古典概型是一种基本的概率模型,用于计算等可能事件的概率。在这种情况下,每个事件都有相同的概率发生。例如,当一枚硬币被抛掷时,正面和反面出现的概率是相等的,因此可以使用古典概型来计算它们出现的概率。
古典概型的计算方法很简单,只需将事件的数量除以总的可能性数量即可。例如,当抛掷一枚硬币时,有两种可能性:正面或反面,因此每种事件的概率为1/2或50%。同样地,当从一组物品中随机选取一个物品时,每个物品被选中的概率都相等,因此每个物品的概率为1/n,其中n是物品的数量。
尽管古典概型在某些情况下可能不适用,但它是计算概率的基础,特别是在更高级的概率模型的构建中。
6. 几何概型
几何概型是一种用于计算概率的模型,适用于连续型随机变量的概率分布。它基于对连续概率分布曲线下面积的计算来确定随机变量落在特定区间的概率。
在几何概型中,概率被视为一个面积,因此该方法通常用于分析几何上的问题。例如,在连续型随机变量X的概率密度函数下,我们可以使用几何概型来计算随机变量落在某个区间[a,b]的概率。这可以通过计算密度函数曲线下[a,b]区间内的面积来实现。
几何概型的使用需要一些数学知识和技巧,例如对积分的理解和计算。但是,它可以用来解决各种与连续型随机变量相关的问题,包括计算期望值、方差和协方差等。
7. 全概率公式
全概率公式是一种用于计算条件概率的公式,它将条件概率与先验概率结合起来,通过先验概率和条件概率的乘积来计算后验概率。
全概率公式通常用于处理有多个可能的事件发生的情况,而这些事件互不独立,即一个事件的发生会影响其他事件的发生概率。在这种情况下,全概率公式可以将事件之间的相互作用考虑在内,从而得出更准确的结果。
全概率公式的公式如下:
P(A) = P(A|B1)P(B1) + P(A|B2)P(B2) + … + P(A|Bn)P(Bn)
其中,A是我们要计算的事件,B1,B2,…,Bn是相互作用的可能事件,并且它们的并集是样本空间。P(B1),P(B2),…,P(Bn)是各自的先验概率,P(A|B1),P(A|B2),…,P(A|Bn)是相应事件的条件概率。
该公式的含义是:事件A的总概率等于所有可能导致事件A发生的情况的概率之和,即先验概率和相应条件概率的乘积之和。
全概率公式是贝叶斯定理的重要组成部分,用于计算后验概率。它在各种实际问题中都有广泛应用,例如在医学诊断、金融风险管理、市场营销等领域中。
8. 贝叶斯公式
贝叶斯公式是一种用于计算条件概率的公式,它是基于贝叶斯定理提出的。贝叶斯公式可以通过先验概率和条件概率来计算后验概率,从而进行更精确的预测和决策。
贝叶斯公式的公式如下:
P(A|B) = P(B|A)P(A) / P(B)
其中,A和B是两个事件,P(A)和P(B)是它们的先验概率,P(B|A)是在A发生的条件下B发生的条件概率,P(A|B)是在B发生的条件下A发生的后验概率。
该公式的含义是:事件B发生的条件下事件A发生的后验概率等于在A发生的条件下B发生的条件概率和A的先验概率的乘积除以B的先验概率。
贝叶斯公式常用于机器学习、人工智能、医学诊断、金融风险管理等领域中。它可以帮助我们基于先验概率和条件概率计算后验概率,从而进行更准确的预测和决策。
9. 先验概率、后验概率
- 后验概率:
事情已经发生,已有结果,求引起这件事发生的因素的可能性,由果求因,即后验概率。
- 与先验概率的关系:
后验概率的计算,是以先验概率为前提条件的。如果只知道时间的结果,而不知道先验概率(没有以往数据统计),是无法计算后验概率的。
后验概率的计算需要应用到贝叶斯公式。
10. 数学期望
数学期望是描述随机变量平均值的一个概念。在概率论和统计学中,数学期望(也称为期望值、平均值或均值)是对一个随机变量取值的加权平均数,其权重由每个取值的概率给出。
对于一个离散随机变量 X,其数学期望 E(X) 定义为:
E(X) = ∑ x * P(X = x)
其中,x 是随机变量 X 所能取到的每一个值,P(X=x) 是随机变量 X 取值为 x 的概率。
对于一个连续随机变量 Y,其数学期望 E(Y) 定义为:
E(Y) = ∫ y * f(y) dy
其中,f(y) 是随机变量 Y 的概率密度函数,y 是随机变量 Y 所能取到的每一个值。
直观来说,数学期望可以理解为随机变量在大量独立实验中出现的平均结果。例如,抛一枚硬币,正面朝上的概率为 0.5,反面朝上的概率也为 0.5。在进行大量独立的抛硬币实验后,正面朝上和反面朝上的次数应该大致相等,因此该随机变量的数学期望为 0.51+0.50=0.5。
相关文章:

考研复试——概率论
文章目录概率论1. 大数定律2. 中心极限定理3. 大数定律和中心极限定理的区别?4. 最大似然估计5. 古典概型6. 几何概型7. 全概率公式8. 贝叶斯公式9. 先验概率、后验概率10. 数学期望因为初试考的数二,没有学概率论,要从头学习时间也不够&…...

Web学习4_JavaScript常用库
常用库 jQuery 使用方式 在元素中添加: <script src"https://cdn.staticfile.org/jquery/1.10.2/jquery.min.js"> </script> 按jQuery官网提示下载 选择器 $(selector),例如: $(div);$(.big-div); $(div > p)s…...
C++回顾(二十)—— vector容器 和 deque容器
20.1 vector容器 20.1.1 vector容器简介 vector是将元素置于一个动态数组中加以管理的容器。vector可以随机存取元素(支持索引值直接存取, 用[]操作符或at()方法)。vector尾部添加或移除元素非常快速。但是在中部或头部插入元素或移除元素比…...

httpd使用记录
httpd使用记录 Busybox用一个httpd的程序,尝试用起来。 简单测试 启动服务 # 启动服务 mkdir /var/www/html httpd -p 8080 -h /var/www/html &编写html文件 在/var/www/html下放一个测试网页index.html文件。 <!DOCTYPE html> <html><hea…...
.vue 组件打包成 .js
.vue 组件打包成 .js *** 所有的内容 cli 官网都有 *** *** https://cli.vuejs.org/zh/guide/build-targets.html *** 所有的内容 cli 官网都有: https://cli.vuejs.org/zh/guide/build-targets.html 准备 几个 .vue 组件文件 import Main from ./components/Ma…...
编程解决数学问题:“计算3个10以内的数字,与合计值相除后,商的第3位小数大于4,共有多少个数的组合满足条件”类似问题)
Java 代码分享(第11篇)编程解决数学问题:“计算3个10以内的数字,与合计值相除后,商的第3位小数大于4,共有多少个数的组合满足条件”类似问题
求与合计相除,小数位大于4的数字组合 1 3 4 9 17 1 / 17 ≈ 0.05882 3 / 17 ≈ 0.17647 4 / 17 ≈ 0.23529 9 / 17 ≈ 0.52941 可以发现,每一个商的第三位都是大于等于5的数,四舍五入后会进位。 下面的程序可以生成符合这样条件的数据。…...

面试题 17.05. 字母与数字
题目链接 面试题 17.05. 字母与数字 mid 题目描述 给定一个放有字母和数字的数组,找到最长的子数组,且包含的字母和数字的个数相同。 返回该子数组,若存在多个最长子数组,返回左端点下标值最小的子数组。若不存在这样的数组&…...

解决Win10图片/文件右键单击自动退出并刷新桌面问题
问题描述 这两天开始不知道怎么回事儿,右键选择图片时候,电脑黑屏且资源管理器自动重启。然后我就开始找很多方法去解决。 我试了很多种复杂的简单的方法,但是只有一种解决了我的问题。 解决方案【解决我的问题】 这个方法如下࿱…...

【代码随想录训练营】【Day39】第九章|动态规划|62.不同路径|63. 不同路径 II
不同路径 题目详细:LeetCode.62 有点简单呀,做类似这种题型时,最好就是先画图: 可以像题目一样,画一个二维表格,表格内的值代表到达这个格子的不同路径总数那么已知,如果图的大小为m 1 || n…...

【Linux】linux | 修改系统编码 | 增加字体处理 | 图片处理字体变成方块
一、说明1、CentOS7二、修改系统编码编辑文件vi /etc/locale.conf修改编码并保存LANGzh_CN.UTF-8配置生效source /etc/locale.conf1)修改系统编码,只是让系统支持中文编码2)不解决文字不显示的问题;往后看三、解决字体不显示问题非…...

R语言介绍及安装教程
R语言是一种免费的开源编程语言和环境,主要用于数据分析、统计建模和可视化。它可以运行在不同的操作系统上,如Windows、MacOS和Linux。R语言具有以下特点:丰富的数据处理和统计分析函数库;易于学习和使用;可以生成高质…...

Linux 练习九 (IPC 消息队列)
文章目录消息队列有亲缘关系的进程使用消息队列通信无亲缘关系的进程使用消息队列通信使用环境:Ubuntu18.04 使用工具:VMWare workstations ,xshell作者在学习Linux的过程中对常用的命令进行记录,通过思维导图的方式梳理知识点&am…...
在Win 11下使用Visual Studio 2019和cygwin编译JBR(Java SDK 17)源码
很多文章介绍了JDK 8和JDK11源码在Linux编译,很少有人介绍了JDK 17在windows的编译过程,所以写了这篇文章,为什么选用JBR 17版本,因为JBR17 版本集成了HotSwapAgent功能,具体HotSwapAgent有什么用,请看我前…...

java基础学习 day51 (匿名内部类)
1. 什么是匿名内部类? 隐藏了名字的内部类,实际名字为:外部类名$序号可以写在成员位置,为没有名字的成员内部类也可以写在局部位置,为没有名字的局部内部类 2. 匿名内部类的格式? new 类名/接口名() { 重…...
Spring MVC程序开发(三大功能)
文章目录一、什么是Spring MVC?1.MVC定义2.MVC与Spring MVC的关系3.创建方式二、Spring MVC的核心功能1.连接功能浏览器获取前端接口和后端程序连接功能实现get和post的区别Spring Boot热部署2.获取参数(1)传递单个参数(2)传递对…...
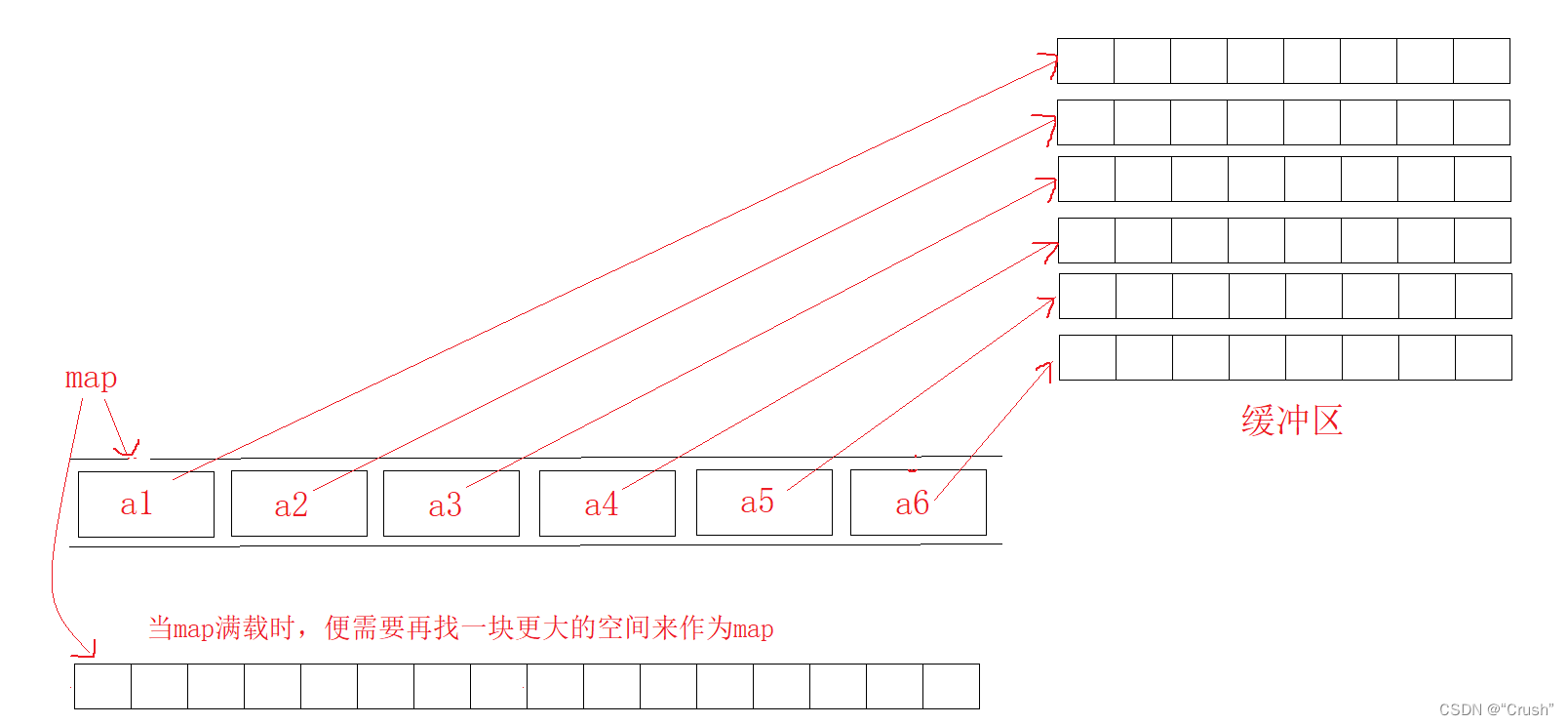
stack,queue
stack,queuestack的介绍和使用介绍使用模拟实现queue的介绍和使用介绍使用模拟实现priority_queue的介绍和使用介绍使用模拟实现容器适配器概念标准库中stack,queue的底层结构介绍deque原理缺陷deque作为stack,queue底层默认容器stack的介绍和使用 介绍 stack是适…...

shiro反序列化
shiro550反序列化 | 清风的博客这个看着更舒服点 环境搭建 JDK:1.7 Tomcat:8.5.83 shiro源码:下载地址:https://codeload.github.com/apache/shiro/zip/shiro-root-1.2.4 shiro war包:下载地址SHIRO-550/samples-…...
)
【GoF 23 概念理解】IoC/DI(控制反转/依赖注入)
搞清楚以下几个问题你就明白什么是 IoC/DI 了: 参与者都有谁?依赖:谁依赖于谁?为什么要依赖?注入:谁注入于谁?到底注入什么?控制反转:谁控制谁?控制什么&…...

stm32外设-GPIO
0. 写在最前 本栏目笔记都是基于stm32F10x 1. GPIO基本介绍 GPIO—general purpose intput output 是通用输入输出端口的简称,简单来说就是软件可控制的引脚, STM32芯片的GPIO引脚与外部设备连接起来,从而实现与外部通讯、控制以及数据采集的…...
AfxMessageBox 自定义封装
一般情况下AfxMessageBox是系统提供的一个对话框,若要做这种效果的,必须重写。 实例1: void test_SgxMemDialog_AutoSize() { //使用给定大小的对话框 CSgxMemDialog dlg(180, 60); dlg.SetWindowTitle(_T(" SegeX - CT&qu…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
