如何理解 IEEE 754 单精度浮点型能表示的最小绝对值、最大绝对值
文章目录
- 解答
- 最小绝对值
- 最大绝对值
- 总结
- 细节理解
- 1. 为什么非规格化数的指数偏移量为126(而不是127)?
- 规格化数与非规格化数
- 非规格化数的指数偏移量
- 非规格化数的尾数
- 非规格化数的值
- 示例
解答
IEEE 754单精度浮点数使用32位来表示一个数值,其格式如下:
- 1位符号位(S):表示数值的正负,0表示正数,1表示负数。
- 8位指数位(E):表示指数部分,使用偏移量127的表示方法。
- 23位尾数位(M):表示小数部分,隐含一个前导1。
根据这个格式可以计算出IEEE 754单精度浮点数能表示的最小绝对值和最大绝对值。
最小绝对值
最小绝对值是指能够表示的最接近于零的正数。对于IEEE 754单精度浮点数,最小绝对值对应于最小指数和最小尾数。
最小指数:指数位全为0,表示非规格化数。非规格化数的指数偏移量为126(而不是127),所以最小指数为 ( E = 1 - 127 = -126 )。最小尾数:尾数位全为0,但非规格化数没有隐含的前导1,所以最小尾数为 ( 0.00000000000000000000001 )(即 ( 2^{-23} ))。
因此,最小绝对值为:
V = 2 − 126 × 2 − 23 = 2 − 149 V = 2^{-126} \times 2^{-23} = 2^{-149} V=2−126×2−23=2−149
最大绝对值
最大绝对值 是指能够表示的最大正数。对于IEEE 754单精度浮点数,最大绝对值对应于最大指数和最大尾数。
最大指数:指数位全为1,表示无穷大或NaN(非数值)。最大有效指数为
E = 254 − 127 = 127 E = 254 - 127 = 127 E=254−127=127最大尾数:尾数位全为1,加上隐含的前导1,所以最大尾数为 ( 1.11111111111111111111111 )(即 ( 2 − 2 − 23 2 - 2^{-23} 2−2−23 ))。
因此,最大绝对值 为:
V = 2 127 × ( 2 − 2 − 23 ) V = 2^{127} \times (2 - 2^{-23}) V=2127×(2−2−23)
总结
- IEEE 754单精度浮点数能表示的
最小绝对值是 ( 2 − 149 2^{-149} 2−149 )。 - IEEE 754单精度浮点数能表示的
最大绝对值是 ( 2 127 × ( 2 − 2 − 23 ) 2^{127} \times (2 - 2^{-23}) 2127×(2−2−23) ),大约是 ( 3.40282347 × 1 0 38 3.40282347 \times 10^{38} 3.40282347×1038 )。
细节理解
1. 为什么非规格化数的指数偏移量为126(而不是127)?
在IEEE 754标准中,非规格化数(也称为次正规数或非正规数)是一种特殊情况,用于表示非常接近于零的数值。为了实现这一目的,IEEE 754标准对非规格化数的指数部分进行了特殊处理。
规格化数与非规格化数
- 规格化数:当指数位不全为0(即 ( 0 < E < 255 ))时,表示规格化数。规格化数的指数偏移量为127,尾数部分隐含一个前导1。
- 非规格化数:当指数位全为0(即 ( E = 0 ))时,表示非规格化数。非规格化数的指数偏移量为126,尾数部分没有隐含的前导1。
非规格化数的指数偏移量
在IEEE 754标准中,规格化数的指数 ( E ) 的实际值是 ( E - 127 )。例如,如果指数位是129,那么实际指数是 ( 129 - 127 = 2 )。
对于非规格化数,指数位全为0,表示 ( E = 0 )。为了确保非规格化数能够平滑地过渡到规格化数,IEEE 754标准规定非规格化数的指数偏移量为126,而不是127。因此,非规格化数的实际指数是 ( 0 - 126 = -126 )。
非规格化数的尾数
对于非规格化数,尾数部分没有隐含的前导1,因此尾数部分的值从 ( 0.0 ) 到 ( 0.11111111111111111111111 )(即 ( 1 - 2 − 23 2^{-23} 2−23 ))。
非规格化数的值
非规格化数的值可以通过以下公式计算:
V = ( − 1 ) S × 2 − 126 × ( 0. M ) V = (-1)^S \times 2^{-126} \times (0.M) V=(−1)S×2−126×(0.M)
其中,( S ) 是符号位,( M ) 是尾数部分。
示例
例如,一个非规格化数的二进制表示为:
0 00000000 00000000000000000000001
- 符号位 ( S = 0 )(正数)
- 指数位 ( E = 0 )(非规格化数)
- 尾数位 ( M = 00000000000000000000001 )(即 ( 2 − 23 2^{-23} 2−23 ))
因此,该非规格化数的值为:
V = 2 − 126 × 2 − 23 = 2 − 149 V = 2^{-126} \times 2^{-23} = 2^{-149} V=2−126×2−23=2−149
相关文章:

如何理解 IEEE 754 单精度浮点型能表示的最小绝对值、最大绝对值
文章目录 解答最小绝对值最大绝对值总结 细节理解1. 为什么非规格化数的指数偏移量为126(而不是127)?规格化数与非规格化数非规格化数的指数偏移量非规格化数的尾数非规格化数的值示例 解答 IEEE 754单精度浮点数使用32位来表示一个数值&…...
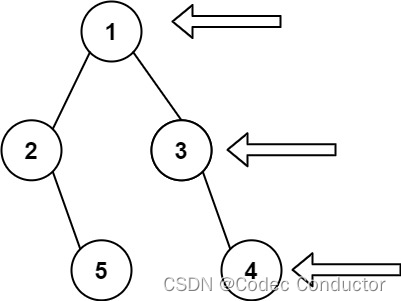
LeetCode 算法:二叉树的右视图 c++
原题链接🔗:二叉树的右视图 难度:中等⭐️⭐️ 题目 给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。 示例 1: 输入: [1,2,3,null,5,null,4…...

Java 并发编程常见问题
1、线程状态它们之间是如何扭转的? 1、谈谈对于多线程的理解? 1、对于多核CPU,多线程可以提升CPU的利用率; 2、对于多IO操作的程序,多线程可以提升系统的整体性能及吞吐量; 3、使用多线程在一些场景下可…...

网络基础:静态路由
静态路由是一种由网络管理员手动配置的路由方式,用于在网络设备(如路由器或交换机)之间传递数据包。与动态路由不同,静态路由不会根据网络状态的变化自动调整。 不同厂商的网络设备在静态路由的配置上有些许差异;下面…...
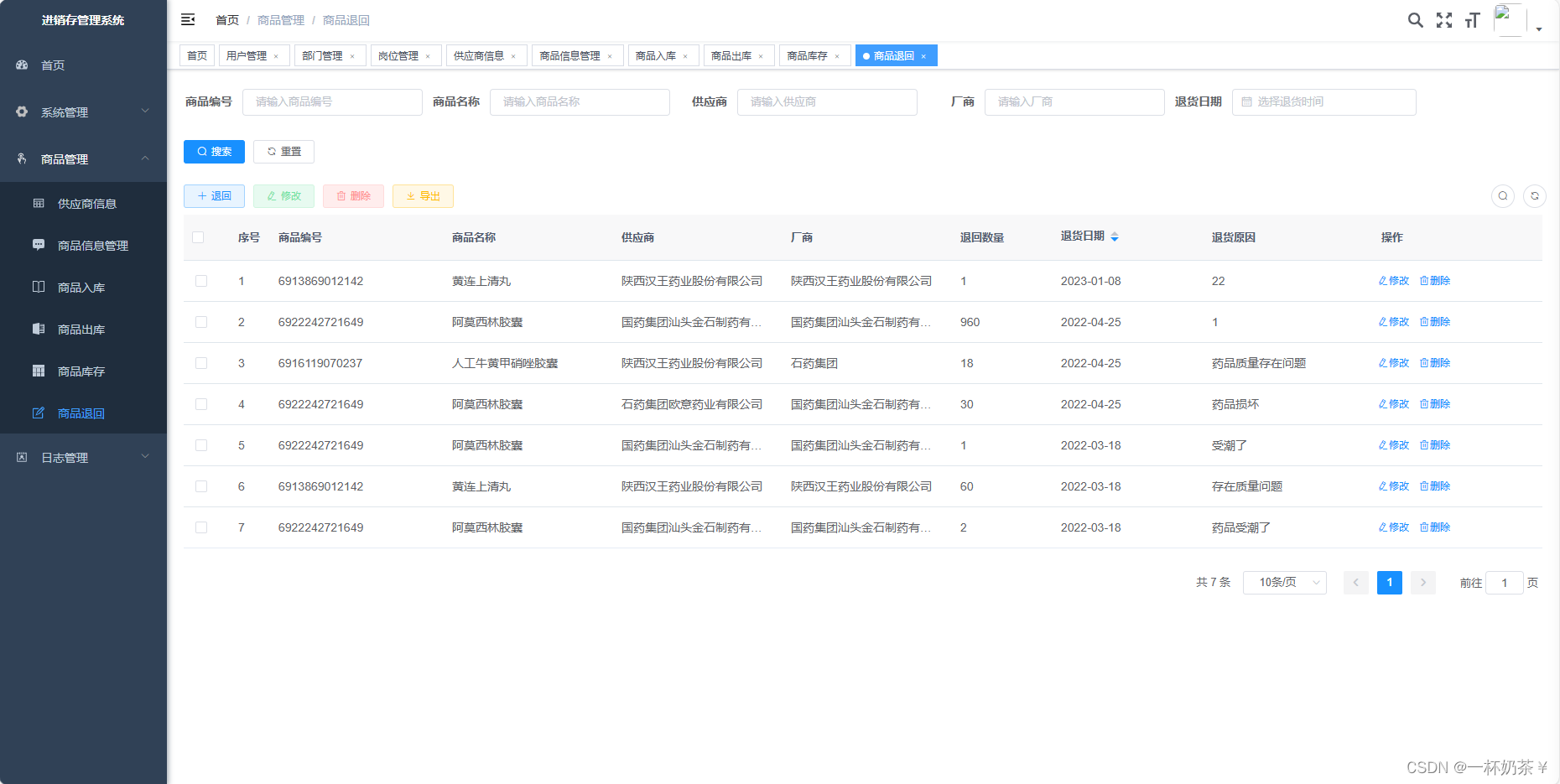
库存管理系统基于spingboot vue的前后端分离仓库库存管理系统java项目java课程设计java毕业设计
文章目录 库存管理系统一、项目演示二、项目介绍三、部分功能截图四、部分代码展示五、底部获取项目源码(9.9¥带走) 库存管理系统 一、项目演示 库存管理系统 二、项目介绍 基于spingboot和vue前后端分离的库存管理系统 功能模块ÿ…...
【ArcGIS AddIn插件】【可用于全国水旱灾害风险普查】全网最强洪水淹没分析插件-基于8邻域种子搜索算法-有源淹没分析算法
最近有很多GIS小伙伴咨询我关于基于8邻域种子搜索算法的有源淹没分析插件的使用方法及原理,咱们通过这篇文章给大家详细介绍下这款插件的运行机制。 一、插件类型及适用版本 本插件属于ArcGIS AddIn工具条插件,基于ArcGIS Engine10.2.2的开发环境开发的&…...
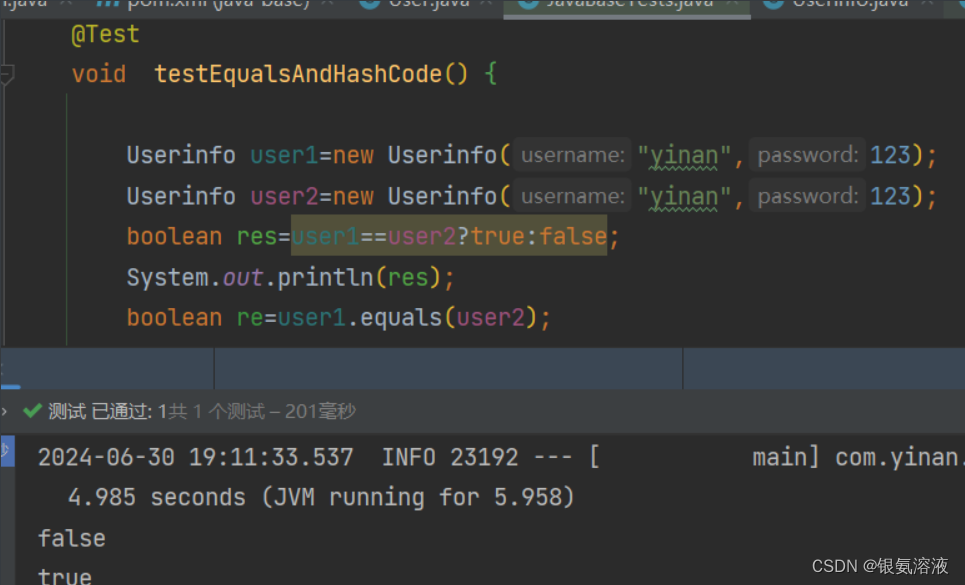
==和equals的区别(面试题)
和equals有什么区别 对于基本数据类型,比较的是值是否相等,对于引用类型则是比较的地址是否相等;对于equals来说,基本数据类型没有equals方法,对于引用类型equals比较的是引用对象是否相同 那针对以上结论,…...
本地项目上传到GitHub上(李豆)
本地项目上传到GitHub上(李豆) 准备工作: 本地需要有 git 也需要有一个 GitHub 账号 首先需要在 GitHub 新建一个空仓库 在想要上传项目的文件夹中使用 Git 命令操作 初始化: git init与 github 仓库进行链接 :git remote add origin …...
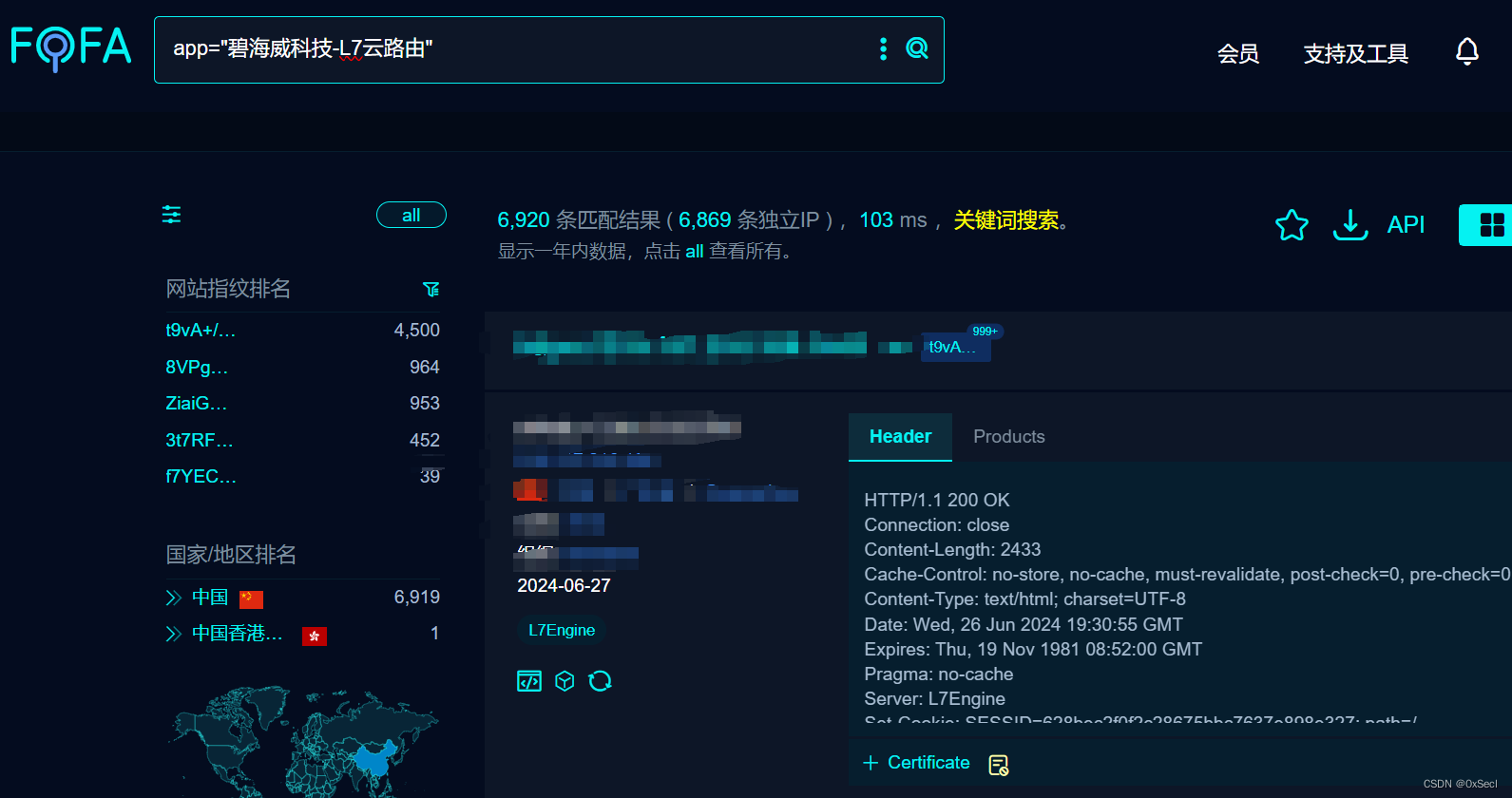
碧海威L7云路由无线运营版 confirm.php/jumper.php 命令注入漏洞复现(XVE-2024-15716)
0x01 产品简介 碧海威L7网络设备是 北京智慧云巅科技有限公司下的产品,基于国产化ARM硬件平台,采用软硬一体协同设计方案,释放出产品最大效能,具有高性能,高扩展,产品性能强劲,具备万兆吞吐能力,支持上万用户同时在线等高性能。其采用简单清晰的可视化WEB管理界面,支持…...
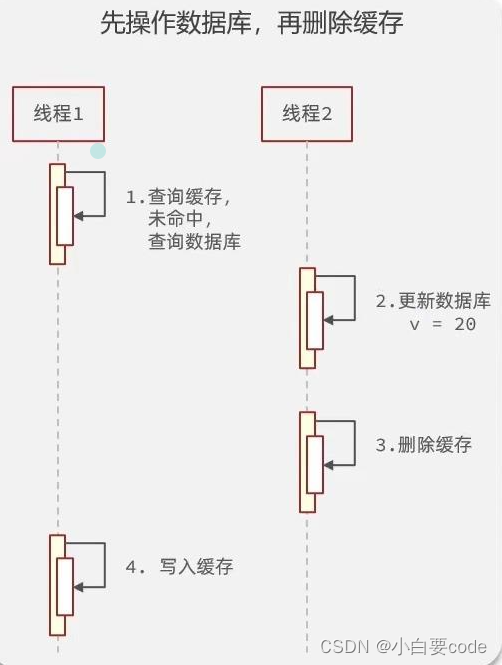
redis实战-添加商户缓存
为什么要使用缓存 言简意赅:速度快,好用缓存数据存储于代码中,而代码运行在内存中,内存的读写性能远高于磁盘,缓存可以大大降低用户访问并发量带来的服务器读写压力实际开发中,企业的数据量,少…...

SQL游标的基本使用方法与示例
SQL游标的基本使用方法与示例 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来探讨SQL游标的基本使用方法及示例。在数据库编程中,游标是一…...

还不知道工业以太网和现场总线区别???
工业以太网 工业以太网是一种专为工业环境设计的网络通信技术,它基于标准的以太网技术,但针对工业应用进行了优化。工业以太网能够适应高温、低温、防尘等恶劣工业环境,采用TCP/IP协议,与IEEE 802.3标准兼容,并在应用层…...
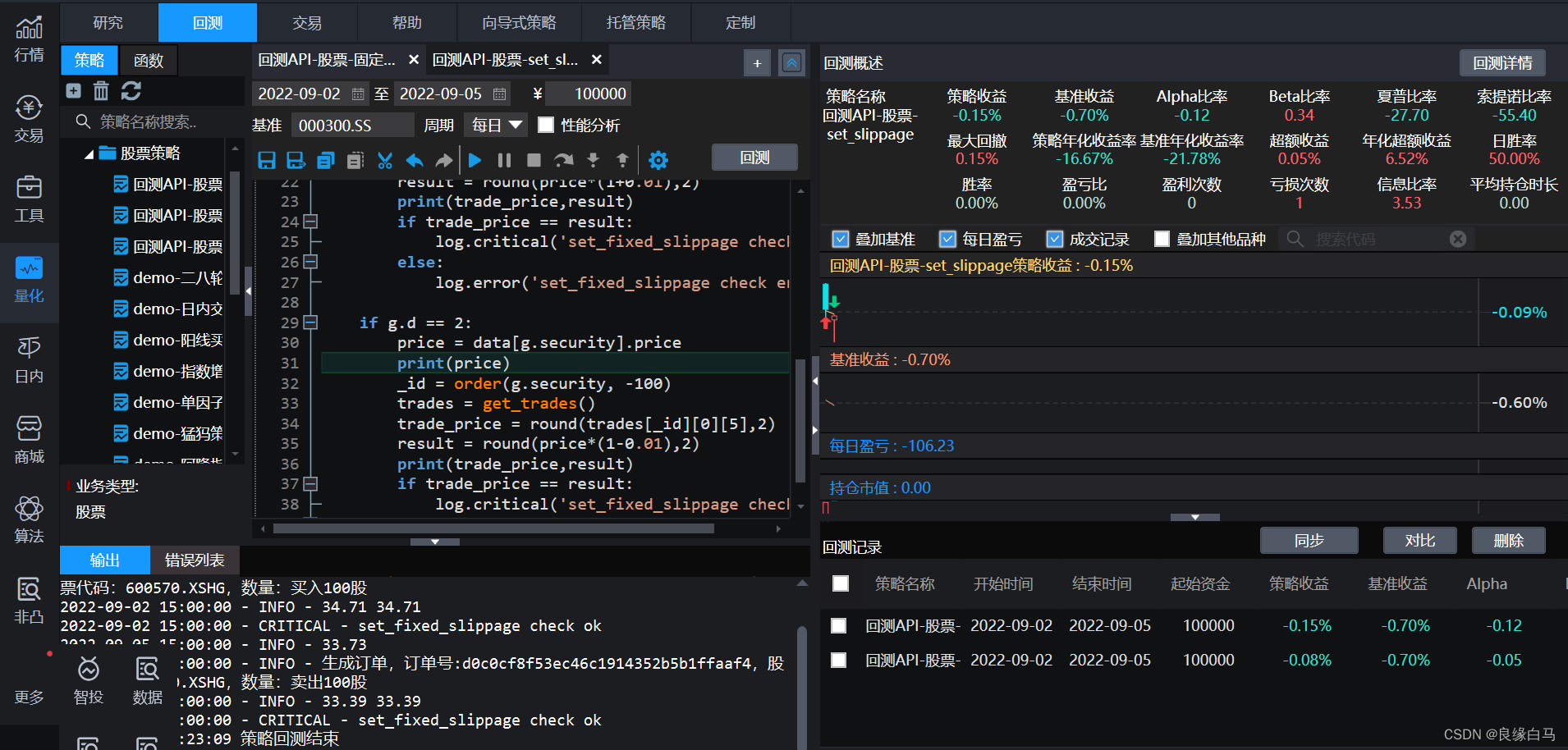
量化交易 - 策略回测
策略回测 1、什么是策略回测?2、策略回测的作用3、策略回测系统概述3.1策略回测中相关的指标介绍3.2量化交易策略的资金容量3.3 完整的策略回测系统包含哪些内容 1、什么是策略回测? 策略回测,也称之为策略回溯测试,是指利用交易…...

Java--选择排序
思想 从左向右遍历数组,让每个数组元素依次作为基准,将基准数组扫描一次,若有元素比基准小则标记这个元素,若后续元素存在比此元素更小的,则标记更小的元素,遍历完此次数组之后,交换基准和标记数…...

Python基础之模块和包
文章目录 1 模块和包1.1 模块和包1.1.1 模块1.1.2 包1.1.3 简单使用 1.2 import 语句1.2.1 import1.2.2 from … import 语句1.2.3 from … import * 语句 1.4 深入模块1.4.1 模块符号表1.4.2 __name__属性1.4.3 dir() 函数1.4.4 作用域 1.5 常用内置模块 1 模块和包 1.1 模块…...
基于SpringBoot漫画网站系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 🌟文末获取源码数据库🌟 感兴趣的可以先收藏起来,…...

Mysql----表的约束
提示:以下是本篇文章正文内容,下面案例可供参考 一、表的约束 表的约束:表中一定要有约束,通过约束让插入表中的数据是符合预期的。它的本质是通过技术手段,让程序员插入正确的数据,约束的最终目标是保证…...

如何用 PHP 实现一个自定义爬虫框架
随着互联网的不断发展,信息量爆炸式增长,获取有价值的信息已经成为了许多人的需求。在这样的大环境下,爬虫技术逐渐兴起,成为了大数据时代的重要工具之一。爬虫技术的应用十分广泛,其可以用于网络舆情监测、数据分析、…...

【机器学习】机器学习的重要方法——强化学习:理论,方法与实践
目录 一、强化学习的核心概念 二、强化学习算法的分类与示例代码 三.强化学习的优势 四.强化学习的应用与挑战 五、总结与展望 强化学习:理论,方法和实践 在人工智能的广阔领域中,强化学习(Reinforcement Learning, RL&…...

Linux磁盘监控思路分析
磁盘监控原理 设备又名I/O设备,泛指计算机系统中除主机以外的所有外部设备。 1.1 计算机分类 1.1.1 按照信息传输速度分: 1.低速设备:每秒传输信息仅几个字节或者百个字节,如:键盘、鼠标等 2.中速设备:…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
