中值滤波+Matlab仿真+频域响应分析
中值滤波
文章目录
- 中值滤波
- 理解中值滤波的过程
- Matlab 实现
- 实际应用
- 频域分析
中值滤波是一种滤波算法,其目的是去除信号中的噪声,而不会对信号本身造成太大的影响。它的原理非常简单:对于一个给定的窗口大小,将窗口内的数值排序,然后使用中间值作为输出。
中值滤波的数学公式如下:
y[n]=median(x[n−k],…,x[n],…,x[n+k])y[n]=\operatorname{median}(x[n-k],\dots,x[n],\dots,x[n+k])y[n]=median(x[n−k],…,x[n],…,x[n+k])
其中 xxx 是原始信号,yyy 是滤波后的信号,nnn 是当前位置,kkk 是窗口大小。
理解中值滤波的过程
为了更好地理解中值滤波的过程,我们可以使用一个简单的数组。假设我们有一个长度为 7 的数组 xxx,如下所示:
x = [1, 3, 2, 4, 6, 5, 7]
现在,我们想对这个数组进行中值滤波,窗口大小为 3。首先,我们需要将窗口移动到数组的第一个元素:
x = [1, 3, 2, 4, 6, 5, 7]^ ^ ^| | || | 窗口最后一个元素| 窗口中间的元素窗口第一个元素
然后,我们需要将窗口内的元素排序:
x = [1, 3, 2, 4, 6, 5, 7]^ ^ ^| | || | 排序后的窗口最后一个元素| 排序后的窗口中间的元素排序后的窗口第一个元素
排序后,我们可以使用排序后的窗口的中间值作为输出。在这个例子中,中间的值是 3,因此输出为 3。
接下来,我们将窗口向右移动一个元素,并重复这个过程,直到处理完整个数组。
x = [1, 3, 2, 4, 6, 5, 7]^ ^ ^| | || | 2| 3,2,41,2,3
经过中值滤波后,结果为:
y = [1, 2, 3, 4, 5, 5, 7]
Matlab 实现
下面是一个简单的 Matlab 实现,使用了 medfilt1 函数:
% 生成一个随机信号
x = [1, 3, 2, 4, 6, 5, 7];% 中值滤波
y = medfilt1(x, 3);
在这个例子中,我们生成了一个长度为 7 的数组,并使用了 medfilt1 函数对数组进行了中值滤波,窗口大小为 3。
y 的输出结果为 [1, 2, 3, 4, 5, 5, 7]。
实际应用
中值滤波广泛应用于信号处理领域,特别是在声音和图像处理中。在声音处理中,中值滤波可以去除录音中的杂音和爆裂声。在图像处理中,中值滤波可以去除图像中的椒盐噪声和斑点噪声。
好的,这里是一个基于虚拟的音频信号的 Matlab 代码例子,演示中值滤波去除噪声的效果,并绘制处理前后的图像进行对比:
% 生成一个包含噪声的虚拟音频信号
Fs = 44100; % 采样频率
t = 0:1/Fs:5; % 时间范围
f1 = 1000; % 基频
f2 = 4000; % 频率偏移量
x = sin(2*pi*f1*t) + sin(2*pi*(f1+f2*t).*t) + 0.1*randn(size(t));% 绘制原始音频信号的时域图和频谱图
subplot(2,2,1)
plot(t,x)
title('原始信号的时域图')
xlabel('时间 (s)')
ylabel('幅值')
subplot(2,2,2)
f = linspace(0,Fs,length(x));
X = fft(x);
plot(f,abs(X))
title('原始信号的频谱图')
xlabel('频率 (Hz)')
ylabel('幅值')% 对音频信号进行中值滤波处理
win_size = 101;
y = medfilt1(x, win_size);% 绘制处理后的音频信号的时域图和频谱图
subplot(2,2,3)
plot(t,y)
title('处理后的信号的时域图')
xlabel('时间 (s)')
ylabel('幅值')
subplot(2,2,4)
Y = fft(y);
plot(f,abs(Y))
title('处理后的信号的频谱图')
xlabel('频率 (Hz)')
ylabel('幅值')
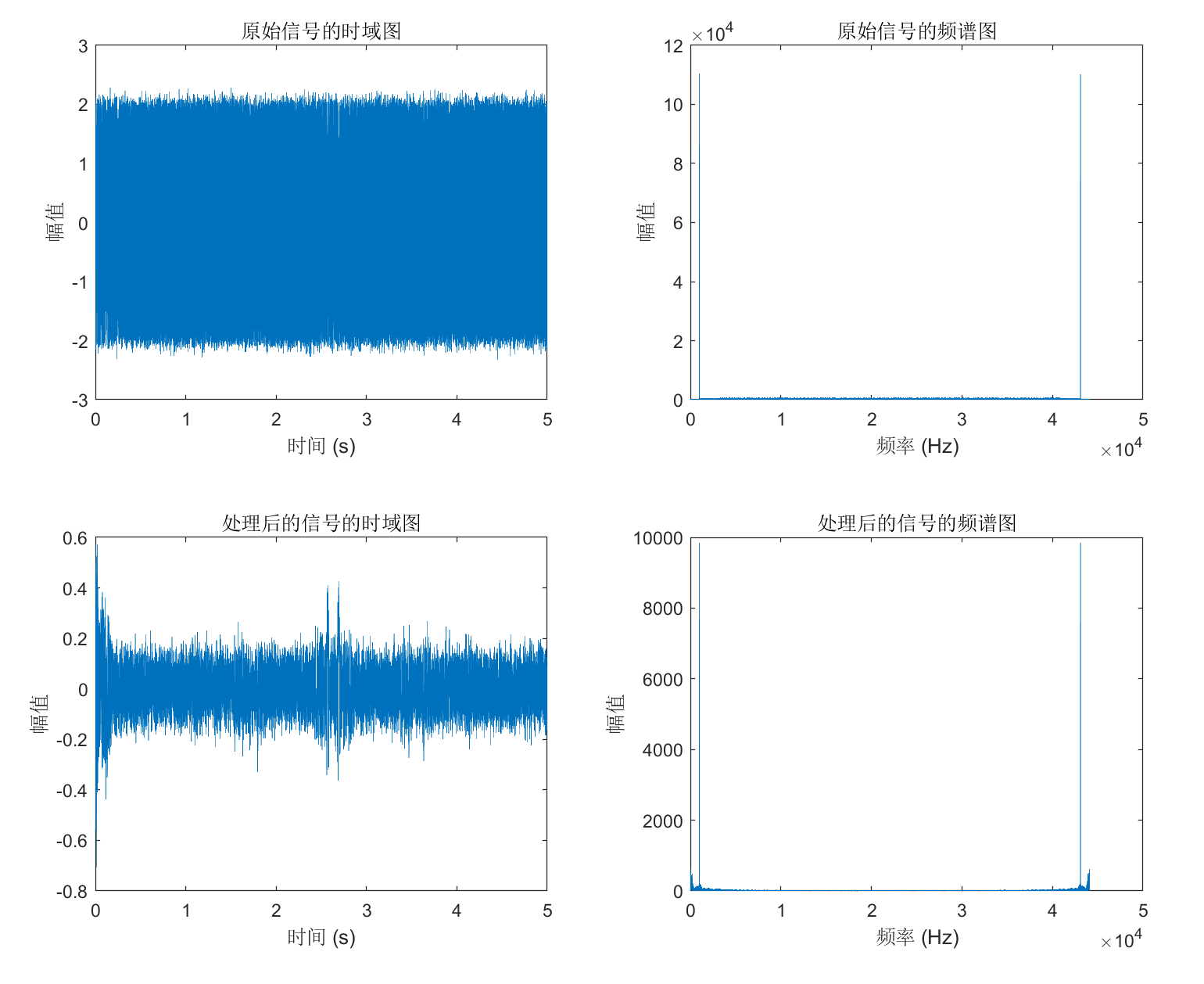
在这个例子中,我们首先生成了一个包含噪声的虚拟音频信号,然后使用 medfilt1 函数对其进行中值滤波处理。接下来,我们绘制了原始音频信号和处理后的音频信号的时域图和频谱图,可以看到,处理后的音频信号的噪声明显减少,幅值更加平滑。
频域分析
从微分方程的角度出发,可以将中值滤波看作是一个差分方程,进而分析其幅频响应。对于一个窗口大小为 3 的中值滤波,其差分方程为:
y[n]=median(x[n−1],x[n],x[n+1])y[n] = \operatorname{median}(x[n-1],x[n],x[n+1])y[n]=median(x[n−1],x[n],x[n+1])
可以将其转化为一个差分方程:
y[n]=12x[n]+14(x[n−1]+x[n+1])y[n] = \frac{1}{2} x[n] + \frac{1}{4} (x[n-1] + x[n+1])y[n]=21x[n]+41(x[n−1]+x[n+1])
其中,x[n]x[n]x[n] 是原始信号,y[n]y[n]y[n] 是滤波后的信号,nnn 是当前位置。
通过对差分方程进行离散化,可以得到其频域响应:
H(ejω)=12+14(e−jω+ejω)H(e^{j\omega}) = \frac{1}{2} + \frac{1}{4} (e^{-j\omega} + e^{j\omega})H(ejω)=21+41(e−jω+ejω)
H(ejω)=12+12cos(ω)H(e^{j\omega}) = \frac{1}{2} + \frac{1}{2} \cos(\omega)H(ejω)=21+21cos(ω)
因此,中值滤波的幅频响应为:
∣H(ejω)∣=(12+12cos(ω))2|H(e^{j\omega})| = \sqrt{\left(\frac{1}{2} + \frac{1}{2} \cos(\omega)\right)^2}∣H(ejω)∣=(21+21cos(ω))2
∣H(ejω)∣=12+12cos(ω)|H(e^{j\omega})| = \frac{1}{2} + \frac{1}{2} \cos(\omega)∣H(ejω)∣=21+21cos(ω)
下面是一个简单的 Matlab 实现,绘制了窗口大小为 3 的中值滤波的幅频响应曲线:
% 绘制窗口大小为 3 的中值滤波的幅频响应曲线
freq = linspace(0, pi, 1000);
H = 0.5 + 0.5*cos(freq);
plot(freq, H)
title('中值滤波的幅频响应')
xlabel('角频率 (rad)')
ylabel('幅值')
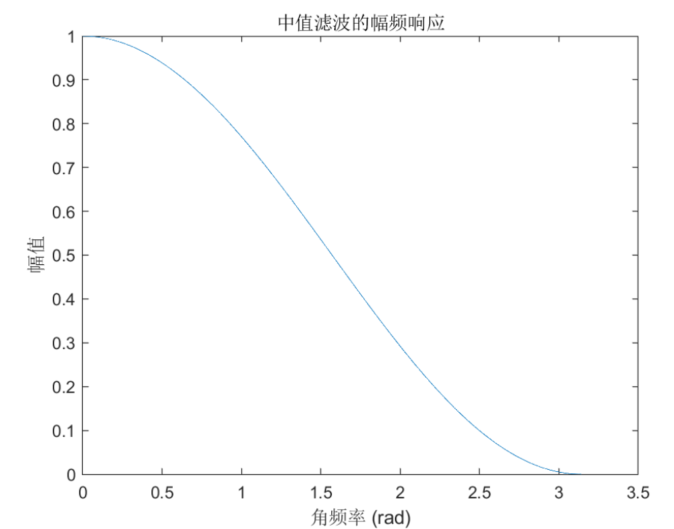
在这个例子中,我们使用 linspace 函数生成了一个包含 1000 个点的频率向量,然后使用中值滤波的幅频响应公式计算了每个点的幅值,并使用 plot 函数绘制了幅频响应曲线。
相关文章:

中值滤波+Matlab仿真+频域响应分析
中值滤波 文章目录中值滤波理解中值滤波的过程Matlab 实现实际应用频域分析中值滤波是一种滤波算法,其目的是去除信号中的噪声,而不会对信号本身造成太大的影响。它的原理非常简单:对于一个给定的窗口大小,将窗口内的数值排序&…...

自然语言处理中数据增强(Data Augmentation)技术最全盘点
与“计算机视觉”中使用图像数据增强的标准做法不同,在NLP中,文本数据的增强非常少见。这是因为对图像的琐碎操作(例如将图像旋转几度或将其转换为灰度)不会改变其语义。语义上不变的转换的存在是使增强成为Computer Vision研究中…...
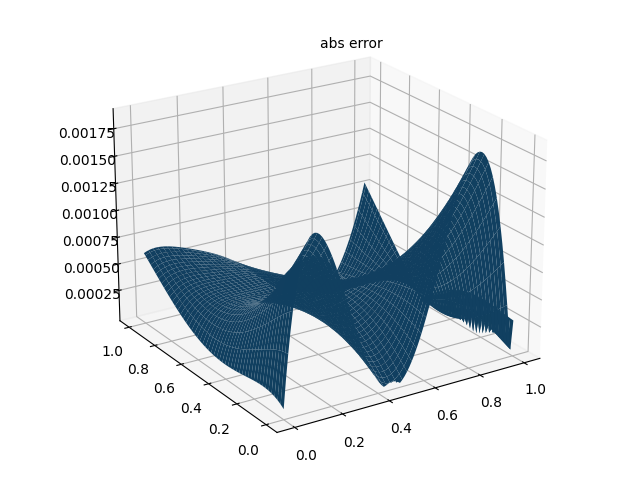
PINN解偏微分方程实例1
PINN解偏微分方程实例11. PINN简介2. 偏微分方程实例3. 基于pytorch实现代码4. 数值解参考资料1. PINN简介 PINN是一种利用神经网络求解偏微分方程的方法,其计算流程图如下图所示,这里以偏微分方程(1)为例。 ∂u∂tu∂u∂xv∂2u∂x2\begin{align} \frac{…...

【python 基础篇 十二】python的函数-------函数生成器
目录1.生成器基本概念2.生成器的创建方式3.生成器的输出方式4.send()方法5.关闭生成器6.注意事项1.生成器基本概念 是一个特色的迭代器(迭代器的抽象层级更高)所以拥有迭代器的特性 惰性计算数据 节省内存 ----就是不是立马生成所有数据,而是…...
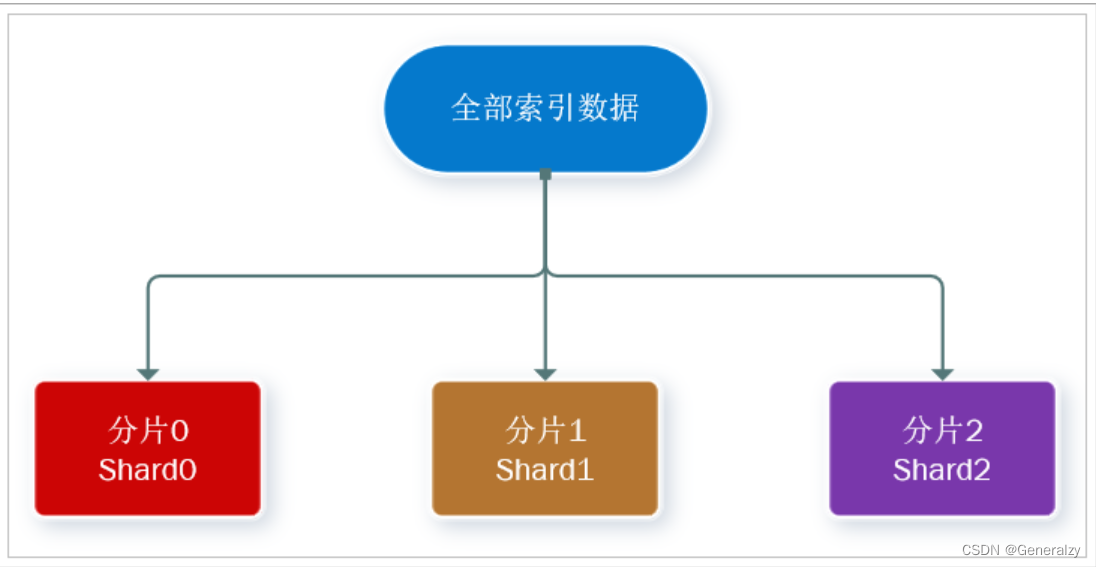
elasticsearch全解 (待续)
目录elasticsearchELK技术栈Lucene与Elasticsearch关系为什么不是其他搜索技术?Elasticsearch核心概念Cluster:集群Node:节点Shard:分片Replia:副本全文检索倒排索引正向和倒排es的一些概念文档和字段索引和映射mysql与…...

springboot2集成knife4j
springboot2集成knife4j springboot2集成knife4j 环境说明集成knife4j 第一步:引入依赖第二步:编写配置类第三步:测试一下 第一小步:编写controller第二小步:启动项目,访问api文档 相关资料 环境说明 …...

Qt 性能优化:CPU占有率高的现象和解决办法
一、前言 在最近的项目中,发现执行 Qt 程序时,有些情况下的 CPU 占用率奇高,最高高达 100%。项目跑在嵌入式板子上,最开始使用 EGLFS 插件,但是由于板子没有单独的鼠标层,导致鼠标移动起来卡顿,…...

MySQL专题(学会就毕业)
MySQL专题0.准备sql设计一张员工信息表,要求如下:编号(纯数字)员工工号 (字符串类型,长度不超过10位)员工姓名(字符串类型,长度不超过10位)性别(男/女,存储一…...

Java高级技术:单元测试、反射、注解
目录 单元测试 单元测试概述 单元测试快速入门 单元测试常用注解 反射 反射概述 反射获取类对象 反射获取构造器对象 反射获取成员变量对象 反射获取方法对象 反射的作用-绕过编译阶段为集合添加数据 反射的作用-通用框架的底层原理 注解 注解概述 自定义注解 …...

C语言初识
#include <stdio.h>//这种写法是过时的写法 void main() {}//int是整型的意思 //main前面的int表示main函数调用后返回一个整型值 int main() {return 0; }int main() { //主函数--程序的入口--main函数有且仅有一个//在这里完成任务//在屏幕伤输出hello world//函数-pri…...

Cadence Allegro 导出Etch Length by Layer Report报告详解
⏪《上一篇》 🏡《上级目录》 ⏩《下一篇》 目录 1,概述2,Etch Length by Layer Report作用3,Etch Length by Layer Report示例4,Etch Length by Layer Report导出方法4.2,方法14.2,方法2B站关注“硬小二”浏览更多演示视频...
无监督对比学习(CL)最新必读经典论文整理分享
对比自监督学习技术是一种很有前途的方法,它通过学习对使两种事物相似或不同的东西进行编码来构建表示。Contrastive learning有很多文章介绍,区别于生成式的自监督方法,如AutoEncoder通过重建输入信号获取中间表示,Contrastive M…...

最长回文子串【Java实现】
题目描述 现有一个字符串s,求s的最长回文子串的长度 输入描述 一个字符串s,仅由小写字母组成,长度不超过100 输出描述 输出一个整数,表示最长回文子串的长度 样例 输入 lozjujzve输出 // 最长公共子串为zjujz,长度为…...

LeetCode 438. Find All Anagrams in a String
LeetCode 438. Find All Anagrams in a String 题目描述 Given two strings s and p, return an array of all the start indices of p’s anagrams in s. You may return the answer in any order. An Anagram is a word or phrase formed by rearranging the letters of a…...
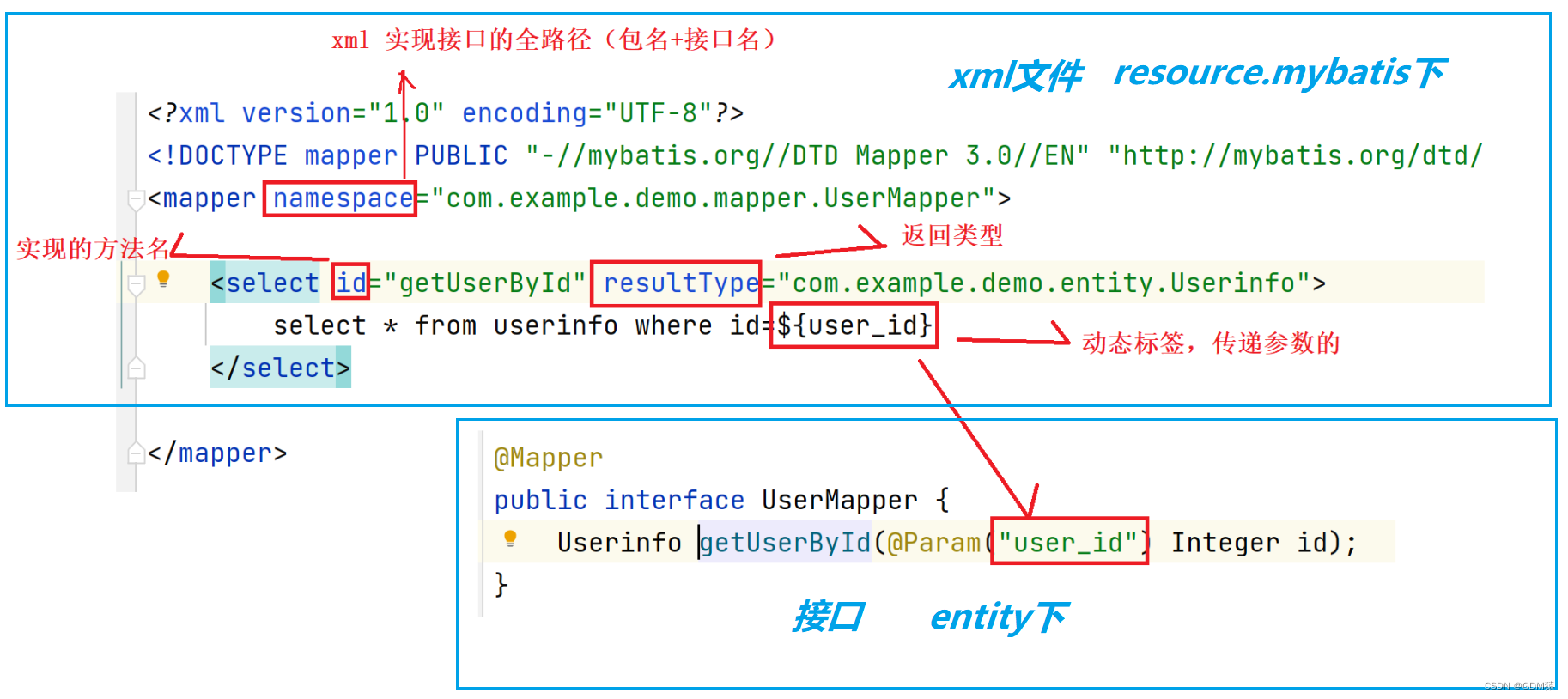
MyBatis-1:基础概念+环境配置
什么是MyBatis?MyBatis是一款优秀的持久层框架,支持自定义sql,存储过程以及高级映射。MyBatis就是可以让我们更加简单的实现程序和数据库之间进行交互的一个工具。可以让我们更加简单的操作和读取数据库的内容。MyBatis的官网:htt…...

R语言基础(五):流程控制语句
R语言基础(一):注释、变量 R语言基础(二):常用函数 R语言基础(三):运算 R语言基础(四):数据类型 6.流程控制语句 和大多数编程语言一样,R语言支持选择结构和循环结构。 6.1 选择语句 选择语句是当条件满足的时候才执行…...

【Java开发】设计模式 02:工厂模式
1 工厂模式介绍工厂模式(Factory Pattern)是 Java 中最常用的设计模式之一。这种类型的设计模式属于创建型模式,它提供了一种创建对象的最佳方式。在工厂模式中,我们在创建对象时不会对客户端暴露创建逻辑,并且是通过使…...
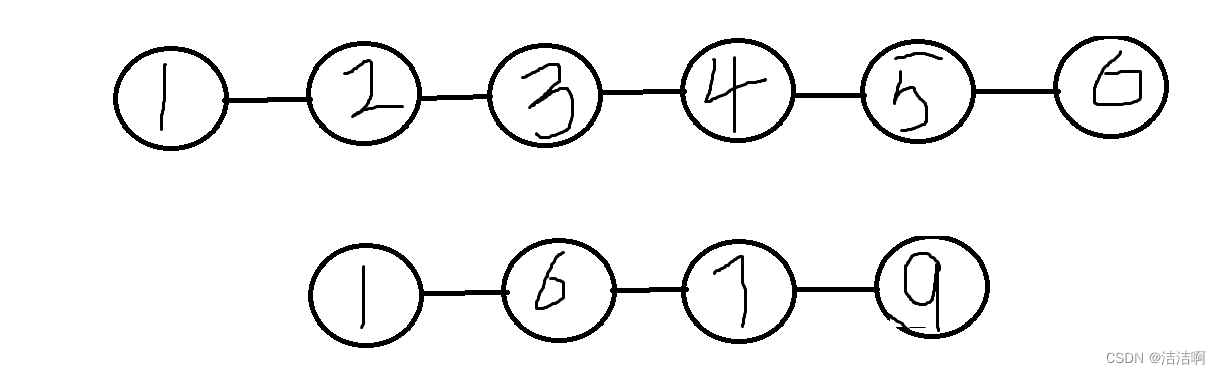
合并两个链表(自定义位置合并与有序合并)LeetCode--OJ题详解
图片: csdn 自定义位置合并 问题: 给两个链表 list1 和 list2 ,它们包含的元素分别为 n 个和 m 个。 请你将 list1 中 下标从 a 到 b 的全部节点都删除,并将list2 接在被删除节点 的位置。 比如: 输入:list1 [1…...

Java编程问题总结
Java编程问题总结 整理自 https://github.com/giantray/stackoverflow-java-top-qa 基础语法 将InputStream转换为String apache commons-io String content IOUtils.toString(new FileInputStream(file), StandardCharsets.UTF_8); //String value FileUtils.readFileT…...

binutils工具集——objcopy的用法
以下内容源于网络资源的学习与整理,如有侵权请告知删除。 一、工具简介 objcopy主要用来转换目标文件的格式。 在实际开发中,我们会用该工具进行格式转换与内容删除。 (1)在链接完成后,将elf格式的.out文件转化为bi…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
